钢管混凝土T型节点在平面内弯曲荷载作用下的静力强度研究

刘洪清，邵永波

(烟台大学土木工程学院，山东 烟台 264005)

钢管结构由于其造型美观及良好的力学性能而在高耸结构、大跨结构和海洋工程中得到广泛应用.在这些结构中，通常将支管直接焊接到主管的外表面形成相贯管节点.实际工程中，管节点的支管主要承受轴向力，所以主管则承受支管传来的径向荷载.相比于支管的轴向刚度，主管的径向刚度较小，再加上主支管相贯区域焊缝处的应力集中以及在焊接过程中产生的残余应力，因此管结构的破坏经常出现在相贯节点处的主管表面.

为改善管节点的受力性能，一般对主支管相贯处的主管部位进行加固，近年来，许多学者提出了不同的加固方法，主要有内部加固法和外部加固法.主管内部加固方法包括内置插板、内置加劲环，以及主管管壁加厚等加固方式[1－4]，主管外部加固方法有环口板加固、垫板加固和肋板加固等方式[5－8].在主管中填充混凝土形成的管节点称为钢管混凝土节点，也相当于主管内部加固的一种方式.文献[9]对圆钢管混凝土K型相贯节点的静力性能进行了试验研究，并提出了该节点极限承载力的计算方法.文献[10]对主管中填充混凝土的X型节点的平面内抗弯性能进行了研究，分析了参数β、γ和τ对节点平面内抗弯承载力和抗弯刚度的影响.文献[11]研究了矩形钢管混凝土T、Y型受压节点的静力性能，分析了节点的破坏模式以及填充在主管内的混凝土对节点受压性能的影响.文献[12]利用试验和有限元的方法研究了N型空心圆钢管节点、垫板加强节点、主管填充混凝土节点以及垫板加强和主管填充混凝土节点的受力性能，研究表明不同加强措施导致节点的不同破坏模态，相对于其他加强措施，主管中填充混凝土能显著提高节点的极限承载力.

目前对于钢管混凝土节点静力强度的研究主要以承受轴力作用为主，但是当支管长细比较小时，节点部位的弯曲作用不能忽略.目前对于钢管混凝土节点在弯曲荷载作用下的性能研究的相关报道很少.因此，本文以钢管混凝土T型节点为研究对象，通过建立可靠的有限元模型，对其在面内弯曲荷载作用下的静力强度进行了分析研究，并探讨了影响承载力大小的因素.

1 有限元模型

1.1 钢管混凝土T型节点有限元模型

主管内填充普通混凝土的圆钢管T型节点几何模型如图1.图1给出了描述几何形状的常用参数，同时用来定义管节点的几个常用无量纲参数β、γ和τ也列于图中.

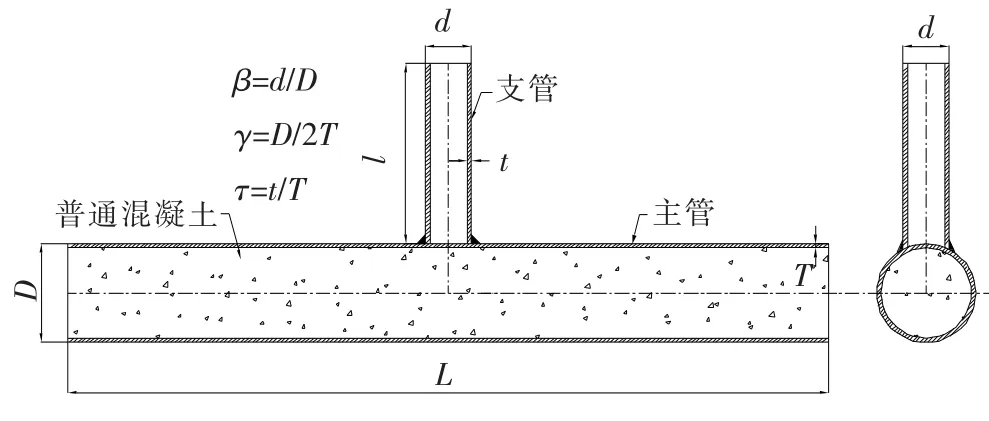
图1 钢管混凝土T型管节点几何模型Fig.1 Geometrical model of a concrete-filled tubular T-joint

在建立有限元模型时，为提高模型的计算精度以及缩短计算时间，需要对模型划分高质量的网格.一般情况下，在应力集中或塑性应变较大的区域应细化网格，即网格的尺寸较小一些，而在其他应力梯度较小的部位可以使网格的尺寸较大一些以便节省计算时间.本文用于模拟钢管混凝土T型管节点的有限元网格如图2，由于节点是应力集中或塑性应变较大的区域，而端部的应力集中现象或塑性应变较小，因此网格的尺寸从主支管相贯区域到主管和支管的端部逐渐变大.另外，由于钢管与混凝土之间有界面接触，在接触分析中定义混凝土为从属表面，其网格尺寸应小于钢管的网格尺寸.同时有限元模型选用的单元类型对计算结果也有很大的影响，通过对文献[12]中N型圆钢管混凝土管节点承载力的模拟，发现主管、支管和混凝土使用三维实体八节点减缩积分单元(C3D8R)得到的结果与试验值吻合较好，所以应用有限元模拟T型管节点的承载力使用C3D8R单元.在节点的材料模型中，钢管采用理想弹塑性模型，不考虑钢材的强度退化，弹性模量为206 GPa，泊松比分0.3.主管内的核心混凝土采用塑性损伤模型，该模型能较好地模拟混凝土的塑性性能以及在往复应力作用下的刚度退化，混凝土的应力－应变关系采用由文献[13]提出的适用于圆钢管混凝土的关系曲线.

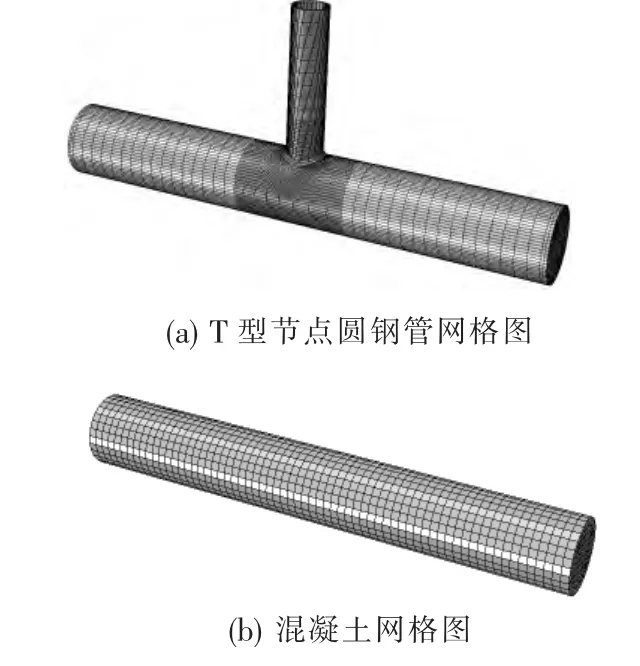
图2 钢管混凝土T型管节点有限元网格Fig.2 Finite element mesh of a T-joint

为了能较好地模拟钢管与混凝土在荷载下的相互作用，需要定义二者间的界面接触.钢管与混凝土在界面法向上采用硬接触，这种接触可以使垂直于接触面的压力完全在界面间传递.切线方向上采用库仑摩擦模型模拟钢管与混凝土在界面切向力的传递，该模型用摩擦系数来表征二者在界面间的摩擦行为，钢管与核心混凝土界面间的摩擦系数取值范围在0.2～0.6之间.经大量模型分析表明，摩擦系数对混凝土管节点承载力的影响很小，而且摩擦系数越小，模型越容易收敛，故建模时取为0.2.有限元模拟T型管节点的承载力时，主管两端均为铰接.

为准确模拟T型节点在平面内弯曲荷载作用下的受力性能，对所有的T型节点模型均模拟了焊缝，焊缝采用和钢管相同的单元类型进行网格离散，详细的焊缝模型见图3.

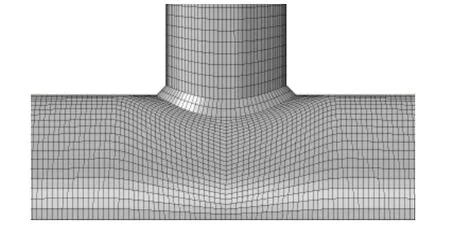
图3 焊缝模型Fig.3 Finite element model of weld

1.2 有限元模型验证

为保证有限元模型的准确性与有效性，在用有限元软件ABAQUS对T型管节点进行承载力分析之前，先用文献[12]中圆钢管混凝土N型相贯节点的承载力试验结果校验所建有限元模型的可靠性，试件的具体几何参数如图4，有限元模型如图5.

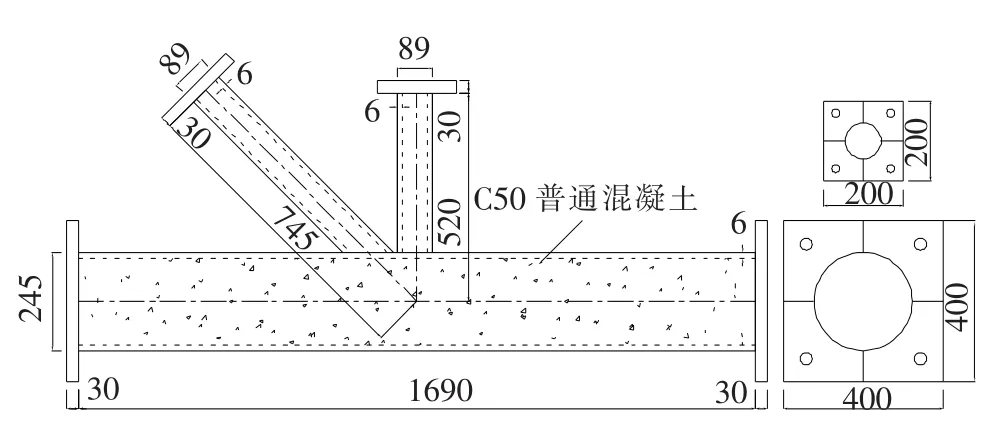
图4 圆钢管混凝土N型管节点的几何尺寸Fig.4 Geometrical dimensions of concrete-filled tubular N-joint

图5 N型管节点有限元模型Fig.5 Finite element model of a N-joint

N型管节点有限元模型完全按照文献中给定的试验条件建立，试验与有限元模拟得到的荷载－变形曲线如图6.荷载指的是竖向受压支管轴向力，变形是受压支管中心线与主管底部的位移差值，即主管管壁变形.由图6可知，有限元结果与试验结果整体吻合较好.造成试验结果和有限元结果之间的误差可能的原因有:混凝土材料本身的离散性、试验试件中混凝土与钢管之间接触的紧密性、主管端部约束的近似化以及加载偏心和试件初始缺陷等.虽然有限元结果和试验结果有误差，但两者的曲线初始刚度和峰值荷载都吻合的比较好，因此采用所建的有限元模型来分析钢管混凝土节点的静力强度是可靠的.

图6 钢管混凝土N型管节点荷载-变形曲线Fig.6 Load-deformation curves of concrete-filled tubular N-joint

此外，为进一步分析核心混凝土节点处的网格密度对计算结果的影响，以表1中第一组CFCT－T1模型为例，分别对核心混凝土节点处的网格不加密以及采取2种不同的网格密度1和2对其进行抗弯承载力有限元分析.核心混凝土节点处的网格加密图见图7(a)、(b).通过有限元软件ABAQUS对模型CFCT－T1在平面内弯曲荷载作用下的静力计算，得到的其弯矩－转角曲线见图8.核心混凝土节点处网格加密与不加密的CFCT－T1节点的抗弯承载力分别为16.86 kN·m和16.36 kN·m，两者之间的误差为3.1%，小于5%，在误差允许范围之内.由于加密核心混凝土节点处的网格，不但使模型耗费大量的计算时间，而且对结果的计算精度影响不大.因此，在保证模型计算结果精度的基础上，为了缩短计算时间，本文采用的核心混凝土节点处网格方案可以取得较高的精度结果，所以在参数分析中可以采用.

图7 核心混凝土在管节点处的网格密度Fig.7 Mesh density of core concrete in the tubular joint

图8 模型CFCT－T1核心混凝土节点处不同网格密度的弯矩－转角曲线Fig.8 Moment-rotation curves of CFCT-T1 model with different mesh density of core concrete in the tubular joint

2 钢管混凝土与空心截面T型管节点静力强度比较

为了分析主管内填混凝土对T型管节点受力性能的影响，选取3个主管内填充混凝土和相应3个空心钢管T型管节点模型进行模拟分析，6个模型的几何尺寸和材料参数如表1所示.表中fy是钢材的屈服强度，fc是混凝土的抗压强度.

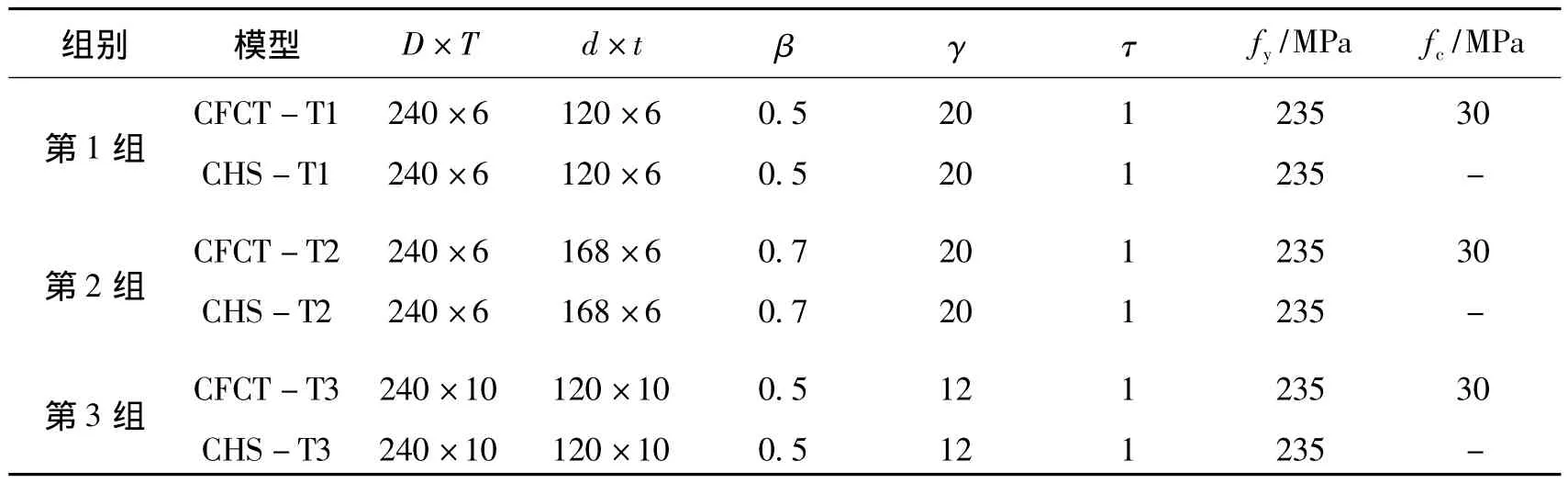
表1 T型管节点几何尺寸和材料参数Tab.1 Geometrical dimensions and material parameters of T-joints

通过在支管端部施加沿主管轴线方向位移，并输出支管端部反力，该反力与支管长度乘积即是节点处的弯矩.转角θ是指支管端部位移与支管长度的比值，以弧度(rad)为单位.6个模型分别在支管端部弯曲荷载作用下得到的弯矩－转角曲线如图9(a)～(c)所示.从图中可以看出，主管中填充混凝土的T型管节点抗弯承载力明显提高.由于空心截面钢管节点和钢管混凝土节点的荷载－位移曲线均未出现下降段，因此不能用峰值荷载确定静力强度，其静力强度的确定采用文献[14]中提出的方法，如图10.首先做一条过原点的直线，再做一条斜率是切线斜率二倍的直线，该二倍弹性斜率直线与曲线的交点所对应荷载即为T型管节点的抗弯承载力.在平面内弯曲荷载作用下，由该方法确定的图9(a)～(c)中，空心截面T型管节点抗弯承载力分别为11.01 kN·m，22.09 kN·m 和20.85 kN·m.主管中填充混凝土相应T型管节点的抗弯承载力分别为16.36 kN·m，39.33 kN·m 和27.57 kN·m.与空心截面管节点相比，钢管混凝土T型管节点的承载力分别提高了48.59%，78.04%，32.23%.由以上分析可知，主管中填充混凝土显著提高了T型管节点的抗弯承载力.从图9(a)～(c)中可以看出，钢管混凝土T型管节点弯矩－转角曲线的斜率明显大于相应的空心截面T型管节点，说明钢管混凝土管节点的刚度也显著提高.

图9 T型节点弯矩－转角曲线Fig.9 Moment-rotation curves of T-joint

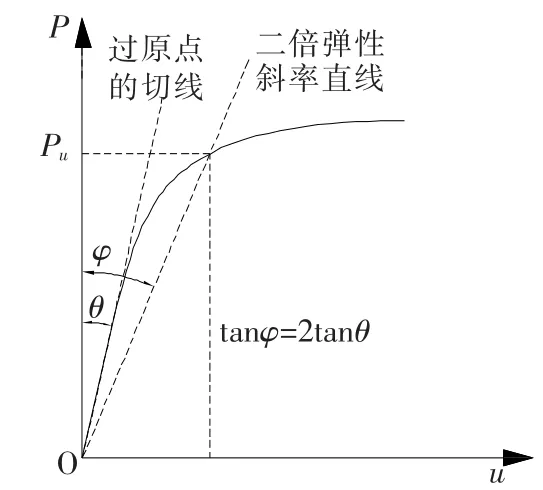
图10 二倍弹性斜率Fig.10 Two-elastic slope

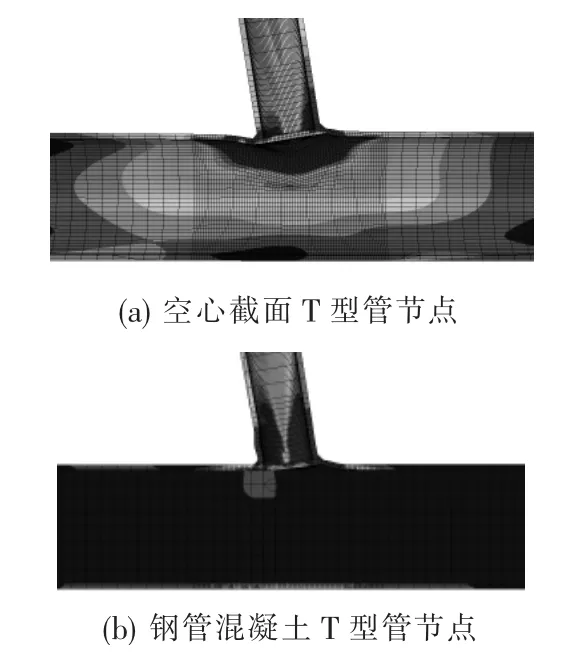
图11 T型管节点破坏模式Fig.11 Failure modes of tubular T-joints

T型管节点的破坏模式如图11(a)、(b)所示，空心截面T型管节点的破坏模式是主支管相贯区域焊缝周围主管表面的屈服破坏，并且屈服首先发生在鞍点处，随后向冠点处扩展，最后整个相贯区域达到屈服.钢管混凝土管节点的破坏模式也是相贯区域焊缝周围主管表面的屈服破坏，但其冠点处首先达到屈服，然后向鞍点区域扩展，并且支管根部也达到屈服.在平面内弯曲荷载作用下，空心截面T型管节点相贯区域的受拉侧和受压侧分别表现出明显的鼓曲和凹陷变形，然而，对于主管中填充混凝土的T型管节点，由于核心混凝土的存在限制了相贯区域主管受压侧的变形，其凹陷变形不明显.此外，T型节点达到极限受弯状态时的应力图见图12(a)、(b)，从图中可以看出，相贯区域处的主管及部分支管的应力均达到235 MPa而进入屈服状态;此时，焊缝的应力也达到235 MPa，但在实际工程中，焊缝由于焊接及处于三向受拉状态而呈现脆性性质，其极限应力高于235 MPa，因此在节点达到极限受弯状态时，焊缝并没有达到极限应力，所以没有发生破坏.

图12 T型管节点应力图Fig.12 Mises stresses of tubular T-joints

3 钢管混凝土T型管节点参数分析

为了进一步分析钢管混凝土T型管节点在平面内弯曲荷载作用下的受力性能，对其进行了参数分析.参数包括:β、γ、τ、fy和 fc.为了减小端部约束对节点域受力性能影响，主管长度取为其直径的7倍，支管长度取为其直径的4倍.模型的具体几何参数见表2.

表2 钢管混凝土T型管节点的参数信息Tab.2 Parameters of CFCT T-joints

通过对18个钢管混凝土T型管节点在平面内弯曲荷载作用下的有限元分析，参数 β，γ，τ，fy，fc对T型节点静力强度的影响如图13(a)～(e)所示.从图13(a)～(c)可以看出，参数β，γ和τ对T节点的静力强度影响较大，其抗弯承载力随着参数β和τ的增大而大幅度提高，随着参数γ的减小而增大.由图13(d)可知，主管中填充混凝土的T型管节点在平面内弯曲荷载作用下，其抗弯承载力随钢材屈服强度fy的提高而增大.这是由于钢管混凝土T型节点的破坏模式为主支管相贯区域及支管根部屈服破坏，因此钢材的屈服强度直接影响到管节点的静力强度，静力强度随钢材屈服强度fy的增加而增大.如图13(e)，混凝土的强度对钢管混凝土T型节点的抗弯承载力影响不大.由于钢管的约束作用，使主管中的核心混凝土处于三向受压状态，在一定程度上提高了混凝土的强度，而混凝土本身具有较好的抗压性能，因此提高混凝土的抗压强度对T型节点的静力强度影响不大.

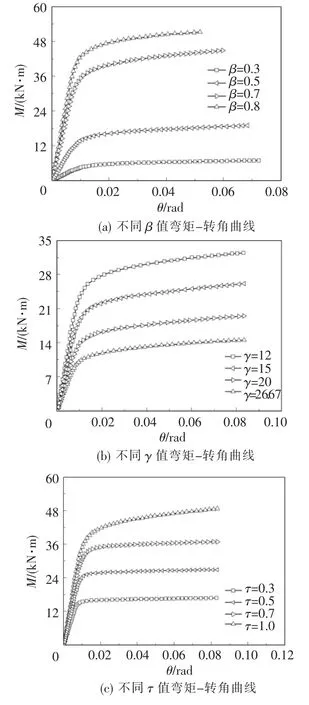
图13 钢管混凝土T型管节点弯矩－转角曲线Fig.13 Moment-rotation curves of concrete-filled tubular T-joints

4 结论

通过对钢管混凝土T型管节点在平面内弯曲荷载作用下的有限元研究，分析了节点的破坏模式以及参数β，γ，τ，fy和fc对其静力强度的影响.可得出以下结论.

(1)与空心截面T型管节点相比，主管中填充混凝土能显著提高T型管节点的抗弯承载力，其破坏模式为主支管相贯区域及支管根部屈服破坏，并且冠点首先进入屈服，随着荷载的增加，屈服范围逐步向鞍点及支管根部扩展.

(2)在几何参数中，T型管节点的承载力随着参数β和τ的增加而增大，随着γ的减小而提高.

(3)在材料参数中，由于钢管混凝土的破坏模式为屈服破坏，因此钢材的屈服强度fy显著影响节点的承载力，其承载力随fy的提高而增大;而主管中的混凝土受到钢管的约束作用，再加上混凝土本身具有较好的抗压性能，故提高混凝土的抗压强度对节点的承载力影响不大.

[1]Lee M M K，Llewelygn-Parry A.Strength predication for ring-stiffened DT-joints in offshore jacket structures[J].Engineering Structures，2005，27(3):421－430.

[2]李涛，邵永波，张季超.内置横向插板加强型管节点静力强度研究[J].钢结构，2009，24(123):25－29.

[3]Yang Jie，Shao Yongbo，Chen Chen.Static strength of chord reinforced tubular Y-joints under axial loading[J].Marine Structures，2012，29(1):226－245.

[4]何树宾，邵永波，张红燕.内置垫板加强T型管节点在平面内弯曲荷载作用下的静力强度研究[J].烟台大学学报:自然科学与工程版，2014，27(1):60－65.

[5]蔡艳青，邵永波，岳永生.环扣板加强型T型圆钢管节点承载力的试验研究[J].工程力学，2011，28(29):91－95.

[6]Choo Y S，Liang J X，van der Vegte G J，et al.Static strength of collar plate reinforced CHS X-joints loaded by inplane bending[J].Journal of Constructional Steel Research，2004，60:1745－1760.

[7]Choo Y S，van der Vegte G J，Zettlemoyer N，et al.Static strength of T-joints reinforced with doubler of collar plates.I:experimental investigation[J].Journal of Constructional Engineering，2005，131(1):118－128.

[8]李涛，邵永波，张季超.肋板加强型管节点静力强度研究[J].建筑结构进展，2012，12(1):51－62.

[9]陈宝春，黄文金.钢管混凝土K型相贯节点极限承载力试验研究[J].土木工程学报，2009，42(12):92－98.

[10]陈誉，张砖湖.主管中灌混凝土平面X形圆钢管混凝土节点平面内抗弯性能试验研究能试验研究[J].土木工程学报，2012，45(8):1－7.

[11]刘永建，周绪红，刘君平.矩形钢管混凝土T、Y型节点受压性能试验[J].长安大学学报:自然科学版，2008，28(5):48－52.

[12]李自林，吴亮秦，朱斌，等.N型圆钢管相贯节点力学性能的试验研究[J].土木工程学报，2008，41(7):48－54.

[13]韩林海.钢管混凝土结构——理论与实践[M].2版.北京:科学出版社，2007.

[14]Shinji K，Masato K，Norihiko M，et al.Plastic collapse load for vessel with external flaw simultaneously subjected to internal pressure and external bending moment:Experimental and FEA results[J].Journal of Pressure Vessel Technology，2009，131:1－10.