关于不定方程x2＋4n＝y11

唐维彬

(西南大学数学与统计学院，重庆 400715)

关于不定方程x2＋4n＝y11

唐维彬

(西南大学数学与统计学院，重庆 400715)

利用代数数论的方法，证明了不定方程x2＋4n＝y11，当n＝3和n＝4时无整数解，n＝5时有整数解(x，y)＝(±32，2).

不定方程;整数解;代数数论

设A，B∈Z＋，A无平方因子，关于不定方程

的解的讨论是代数数论中的一类重要课题.当A＝1，B＝1时，LEDESGUE证明了式(1)无整数解;NAGELL证明了当A＝2，B＝1，n＝5时，式(1)仅有整数解(x，y)＝(±11，3);对于A＝1，B＝43或44，n＝5，7时的情况文献［1－7］均已讨论过;李中恢，张四保［8］证明了关于不定方程x2＋16＝y11无整数解;而对于A＝1，n＝11，B＝43，44或45时的情况未曾讨论.因此，此处讨论了当A＝1，n＝11，B＝43，44或45时的情况.

引理1设M是唯一分解整环，正整数k≥2，以及α，β∈Z，(α，β)＝1，那么若αβ＝γk，γ∈M，则有α＝ε1μk，β＝ε2νk，μ，ν∈M，其中ε1，ε2是M中的单位元素，并且ε1ε2＝εk，ε为单位元素.

定理1不定方程

无整数解.

证明这里分x≡1(mod 2)，x≡0(mod 2)两种情况进行讨论.

1)先假设x≡1(mod 2)，在Z［i］中，方程(2)可以写为(x+23i)(x－23i)=y11，x，y∈Z

设δ＝(x＋23i，x－23i)，由δ|(2x，24i)＝2，知道δ只能是1，1＋i，2.由x≡1(mod 2)知道，x＋23i≡1(mod 2)，所以δ≠2;如果δ＝1＋i，则N(1＋i)|N(x＋23i)，可知2|x2＋43，这与x≡1(mod 2)矛盾，所以δ＝1.由此知x＋23i＝(a＋bi)11，x，a，b∈Z，因而有

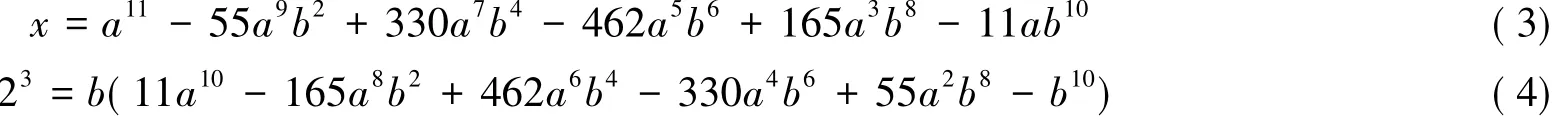
从式(4)中可以得到b＝±1，±2t(1≤t≤2)，±23.

当b＝±1时，1±23＝11(a10－15a8＋42a6－30a4＋5a2)，等式两边同时取模11，得到9≡0(mod 11)或者4≡0(mod 11)，这是矛盾的.

当b＝±2t(1≤t≤2)，±23－t=11a10－165a8b2+462a6b4－330a4b6+55a2b8－b10，两边同时取模2，得到0≡a10(mod 2)，从而a必为偶数，然后再由x=a11－55a9b2+330a7b4－462a5b6+165a3b6－11ab6知x也为偶数，这与假设x≡1(mod 2)矛盾.

当b＝23时，1＋230＝11a10－165a8b2＋462a6b4－330a4b6＋55a2b8，等式两边同取模11得2≡0(mod 11)，这是不可能的.

当b＝－23时，a2(11a8－165a6b2+462a4b4－330a2b6+55b8)=230－1=32×7×11×31×151×331，因为a∈Z，所以a2＝1或9，代入验证如下:

当a2＝1时，b＝－23，11a10－165a8b2+462a6b4－330a4b6+55a2b8－b10=－235 620 661≠－1.

当a2＝9时，b＝－23，11a10－165a8b2+462a6b4－330a4b6+55a2b8－b10=1 534 760 963≠－1.

综上所述，当x≡1(mod 2)时，原方程无整数解.

2)再讨论x≡0(mod 2)的情况，也就是x为偶数，容易知道y也是偶数，所以令x＝2x1，y＝2y1，x1，y1∈Z.此时方程变为

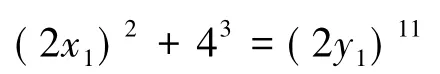
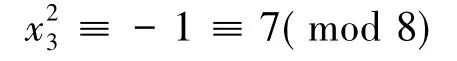
由数论的知识可以知道，7是模8的二次非剩余，也即x23≡－1≡7(mod 8)无解，所以当x≡0(mod 2)时式(2)无整数解.

定理2不定方程

无整数解.

证明这里分x≡1(mod 2)，x≡0(mod 2)两种情况进行讨论.

1)先假设x≡1(mod 2)，在Z［i］中原方程可以写为

(x+24i)(x－24i)=y11，x，y∈Z

设δ＝(x＋24i，x－24i)，由δ|(2x，25i)＝2，知道δ只能是1，1＋i，2.由x≡1(mod 2)，知道x＋24i≡1(mod 2)，所以δ≠2;如果δ＝1＋i，则N(1＋i)|N(x＋24i)，即2|x2＋44，与x≡1(mod 2)产生矛盾，因此δ＝1.由此知x＋24i＝(a＋bi)11，x，a，b∈Z，因而有

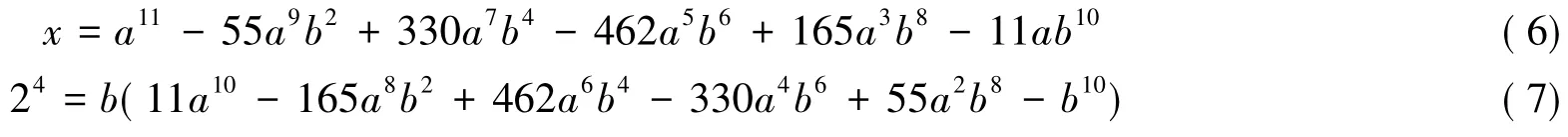
因此b＝±1，±2t(1≤t≤3)，±24.

当b＝±1时，1±24＝11(a10－15a8＋42a6－30a4＋5a2)，此式要成立需满足11|1±24，但这是不可能的.

当b＝±2t(1≤t≤3)时，±24－t＝11a10－165a8b2＋462a6b4－330a4b6＋55a2b8－b10，则a必为偶数，再由x＝a11－55a9b2＋330a7b4－462a5b6＋165a3b6－11ab6知x也为偶数，这与假设x≡1(mod 2)矛盾.

当b＝24时，1＋240＝11a10－165a8b2＋462a6b4－330a4b6＋55a2b8，等式两边同取模11得2≡0(mod 11)，这是不可能的.

当b＝－24时，11a10－165a8b2+462a6b4－330a4b6+55a2b8=240－1=3×52×11×17×31×41× 61 681，由于a∈Z，所以a2＝1或25.下面讨论两种情况得到:

当a2＝1时，b＝－24时，11a10－165a8b2+462a6b4－330a4b6+55a2b8－b10=－868 794 672 373≠－1.

当a2＝25时，b＝－24，11a10－165a8b2+462a6b4－330a4b6+55a2b8－b10=1 802 463 026 099≠－1.

综上所述，当x≡1(mod 2)时，原方程无整数解.

2)再讨论x≡0(mod 2)的情况.易知y也是偶数，令x＝2x1，y＝2y1，x1，y1∈Z.此时方程可变为(2x1)2＋ 44＝(2y1)11，即，易知x1仍为偶数，令x1＝2x2，得x22＋42＝27y71，此时x2也为偶数，再令x2＝2x3，x3∈Z，得x23＋4＝25y72，仍有x3为偶数，令x3＝2x4，得x24＋1＝8y71，由于x4是奇数，取mod 8.可知该方程无整数解，故当x≡0(mod 2)时，不定方程x2＋44＝y11无整数解.综上讨论，不定方程x2＋44＝y11无整数解.

定理3不定方程

有整数解(x＝±32，y＝2).

证明这里分x≡1(mod 2)，x≡0(mod 2)两种情况进行讨论.

1)先假设x≡1(mod 2)，在Z［i］中原方程可以写为(x+25i)(x－25i)=y11，x，y∈Z

设δ＝(x＋25i，x－25i)，由δ|(2x，26i)＝2，知道δ只能是1，1＋i，2.因x≡1(mod 2)知道x＋25i≡1(mod 2)，所以δ≠2;如果δ＝1＋i，则N(1＋i)|N(x＋25i)，即2|x2＋45，与x≡1(mod 2)产生矛盾，因此δ＝1.由此知x＋25i＝(a＋bi)11，x，a，b∈Z，因而有

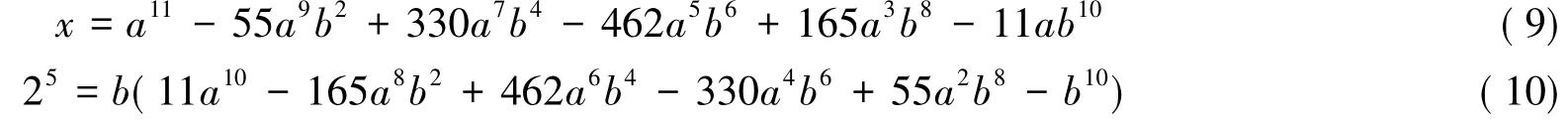
因此b＝±1，±2t(1≤t≤4)，±25.

当b＝－1时，1－24＝11(a10－15a8＋42a6－30a4＋5a2)，此式要成立需满足11|1－25，但这是不可能的.

当b＝1时，1＋25＝33＝11(a10－15a8＋42a6－30a4＋5a2)，得到a2＝1，但x＝a11－55a9b2＋330a7b4－462a5b6＋165a3b6－11ab6，此时x为偶数，与假设矛盾，这是不可能的.

当b＝±2t(1≤t≤4)时，±25－t＝11a10－165a8b2＋462a6b4－330a4b6＋55a2b8－b10，则a必为偶数，再由x＝a11－55a9b2＋330a7b4－462a5b6＋165a3b6－11ab6知x也为偶数，这与假设x≡1(mod 2)矛盾.

当b＝25时，1＋250＝11a10－165a8b2＋462a6b4－330a4b6＋55a2b8，等式两边同取模11得2≡0(mod 11)，这是不可能的.

当b＝－25时，11a10－165a8b2+462a6b4－330a4b6+55a2b8=250－1=3×11×31×251×601×1 801× 4 051，由于a∈Z，所以a2＝1.当a2＝1时，b＝－25时，11a10－165a8b2+462a6b4－330a4b6+55a2b8－b10=－1 065 780 617 843 701≠－1.

综上所述，当x≡1(mod 2)时，原方程无整数解.

2)再讨论x≡0(mod 2)的情况，也就是x为偶数，容易知道y也是偶数，所以令x＝2x1，y＝2y1，x1，y1∈Z.此时方程变为

(2x1)2+45=(2y1)11

即x21＋44＝29y111(x1，y1∈Z)，易知x1仍为偶数，且能被4整除，令x1＝4x2，得x22+42=25y111，此时x2也为偶数，且能被4整除，再令x2＝4x3，得x23＋1＝2y111，由于2y111是偶数，所以x3必为奇数.只需讨论x2＋1＝2y111的整数解.在Z［i］中此方程可以写为

(x+i)(x－i)=i(1－i)2y11

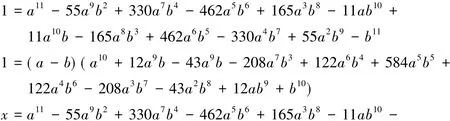
［1］潘承洞，潘承彪.代数数论［M］.济南:山东大学出版社，2003

［2］高丽，马永刚.关于不定方程x2＋42＝y7［J］.西南民族大学学报，2008，34(1):27－29

［3］张杰.关于不定方程x2＋43＝y7的解［J］.重庆工商大学学报:自然科学版，2012，29(3):27－28

［4］冉银霞.关于不定方程x2＋44＝y7［J］.延安大学学报:自然科学版，2012，31(4):14－15

［5］冉银霞.关于不定方程x2＋46＝y7［J］.高师理科学刊，2013，33(4):25－26

［6］王振，张慧.关于Diophantine方程x2＋4n＝y3［J］.重庆工商大学学报:自然科学版，2010，27(6):220－222

［7］崔保军.关于不定方程x2＋4n＝y5［J］.湖北民族学院学报:自然科学版，2011，29(1):49－50

［8］李中恢，张四保.关于不定方程x2＋16＝y11［J］.海南大学学报:自然科学版，2009，27(3):216－218

On the Diophantine Equation x2＋4n＝y11

TANG Wei-bin

(School of Mathematics and Statistics，Southwest University，Chongqing 400715，China)

By using the method of algebraic number theory，the Diophantine equation x2＋4n＝y11has no integer solution when n＝3，4，and has integer solution(x，y)＝(±32，2)when n＝5.

the Diophantine equation;integer solution;algebraic number theory

O156

A

1672－058X(2015)01－0015－04

10.16055/j.issn.1672－058X.2015.0001.005

责任编辑:李翠薇

2014－06－09;

2014－07－09.

唐维彬(1990－)，男，重庆南岸人，硕士研究生，从事计算数论研究.