广义不变凸单调准则

向丽娟

(重庆师范大学数学学院，重庆 401331)

广义不变凸单调准则

向丽娟

(重庆师范大学数学学院，重庆 401331)

在η关于第一变量仿射且是skew函数条件下，推出伪不变凸单调与严格伪不变凸单调之间的关系.

伪不变凸;广义不变凸;仿射

广义凸在数学、管理科学、工程学、经济学和最优化理论中都担当了重要的角色，不变凸函数和不变凸单调又是研究广义凸性的重要组成部分，文献［1－4］研究了关于广义不变凸与不变凸单调;文献［4］在η关于第一变量仿射且是skew函数条件代替条件C下，建立了伪不变凸单调与拟不变凸单调之间的关系.而此处是在η关于第一变量仿射且是skew函数条件下，推出伪不变凸单调与严格伪不变凸单调之间的关系.

1 预备知识

定义1［5］设X和Y是实向量空间，若函数φ:X→Y的映射，对∀x，y∈X，且∀λ，μ∈R，有

φ(λx+μy)=λφ(x)+μφ(y)

成立，则称φ是线性函数.

定义2［6］设Γ⊆Rn是凸集，若函数φ:Γ⊆Rn→Rn的映射，对∀x，y∈X，且∀λ∈(0，1)，有φ(λx+(1－λ)y)=λφ(x)+(1－λ)φ(y)

成立，则称φ是仿射函数.

定义3［1］设函数η:Γ×Γ→Rn，若对∀x，y∈Γ⊆Rn都有η(x，y)+η(y，x)=0

成立，则称η为skew函数.

定义4［1］设Γ⊆Rn是开集，函数θ:Γ⊆Rn→Rn映射，

(a)若∃η:Γ×Γ→Rn对∀x，y∈Γ⊆Rn，都有η(y，x)t▽θ(x)≥0⇒θ(y)－θ(x)≥0

成立，则称θ是伪不变凸单调函数.

(b)若∃η:Γ×Γ→Rn对∀x，y∈Γ⊆Rn，x≠y，都有η(y，x)t▽θ(x)≥0⇒θ(y)－θ(x)＞0

成立，则称F是严格伪不变凸单调函数.

2 主要结果

引理1［4］设集合Γ是集合Rn中的开凸子集，假设:

(a)▽θ:Rn→Rn是关于函数η:Γ×Γ→Rn的严格伪不变凸单调;(b)η关于第一变量仿射且是skew函数;(c)对x≠y，都有成立，其中是x与y线段上一点.则称θ:Γ⊆Rn→ R在Γ关于η是严格伪不变凸的.

定理1设集合Γ是集合Rn中的开凸子集，假设:

(a)▽θ:Rn→Rn是关于函数η:Γ×Γ→Rn伪不变凸单调的;(b)η关于第一变量仿射且是skew函数; (c)对x≠y，都有成立，其中x＝λx＋(1－λ)y，∀0＜λ＜1.则称θ:Γ⊆Rn→ R在Γ关于η是严格伪不变凸的.

证明设∀x，y∈Γ⊆Rn，x≠y，有η(y，x)t▽θ(x)≥0，需要证明θ(x)＞θ(y).反证法，假设θ(x)≤ θ(y)由定理1中的条件(c)知

由定理1中的条件(b)知η关于第一变量仿射且是skew函数条件，有

由式(1)和定理1中的条件(a)知

由式(2)和定理中1的条件(b)有

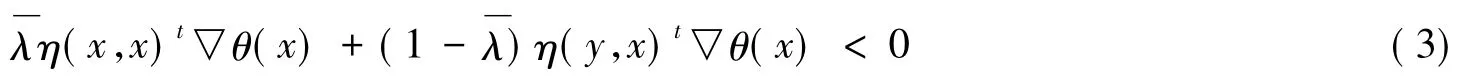
由η是skew函数，则有

与式(1)矛盾.证毕.

［1］RUIZ G G，OSUNA G R，RUFIAN L A.Generalized Invex Monotonicity［J］.European Journal of Operational Research，2003 (144):501－512

［2］YANG X M，YANG X Q，TEO K L.Criteria for Generalized Invex Monotonicities［J］.European Journal of Operations Research，2005(164):115－119

［3］YANG X M，YANG X Q，TEO K L.Generalized Invexity and Generalized Invariant Monotonicity［J］.Journal of Optimization Theory and Applications，2003(117):607－625

［4］PENG J W.Criteria for Generalized Invex Monotonicities without Condition C［J］.European Journal of Operations Research，2006 (170):667－671

［5］RUBIN W.Functional Analysis［M］.New York:McGraw－Hill，1991

［6］JABARPPTOAN T，ZAFARANI J.Generalized Invariant Monotonicity and Invexity of Non－differentiable Functions［J］.Journal of Global Optimization，2006(36):537－564

［7］张其茂.一类B－预不变凸目标规划的最优性充分条件［J］.重庆工商大学学报:自然科学版，2009，30(6):526－528

Criteria for Generalized Invex Monotonicity

XIANG Li-juan

(School of Mathematics，Chongqing Normal University，Chongqing 401331，China)

The relation between pseudo－invex monotonicity and strictly pseudo－invex monotonicity is derived under the condition that η is the affine in the first argument and is skew function.

pseudo－invexity;generalized invexity;affine

O177

A

1672－058X(2015)01－0013－02

10.16055/j.issn.1672－058X.2015.0001.004

责任编辑:李翠薇

2014－06－11;

2014－07－09.

向丽娟(1989－)，女，重庆巫溪人，硕士研究生，从事凸分析研究.