一种充分下降的CD共轭梯度法及其收敛性*
马烁,王安平
(荆州理工职业学院,湖北 荆州 434000;长江大学工程技术学院,湖北 荆州 434020)
一种充分下降的CD共轭梯度法及其收敛性*
马烁,王安平**
(荆州理工职业学院,湖北 荆州 434000;长江大学工程技术学院,湖北 荆州 434020)
基于已有的CD方法,提出了一种改进的CD共轭梯度法(MCD算法).该算法产生的搜索方向为充分下降方向,且这一性质与所采用的线搜索方法无关;并在一定的条件下证明了该算法基于Wolfe线搜索求解非凸优化问题的全局收敛性.
无约束最优化;共轭梯度法;Wolfe线搜索;全局收敛性
0 引言
考虑无约束优化问题

其中f:Rn→R连续可微.共轭梯度法是求解该问题的一类有效算法.
一般的共轭梯度法的迭代公式为

其中,x1为初始点,dk为搜索方向,αk由某种线性搜索或由特定公式计算出的步长因子,βk为标量,gk=▽f(xk).
共轭梯度法的关键是选取αk和βk,不同的αk和βk决定了不同的共轭梯度算法.常用选取αk的线搜索是标准Wolfe线搜索,即选取αk>0满足

其中δ和σ是满足0<δ<σ<1的常数;而βk的选取公式常用的有

在众多共轭梯度法中,为了保证是下降方向,许多学者都做了深入的研究.文献[7]提出一种新的谱DY共轭梯度法(简记为MDY),其迭代格式为式(2)和


受到文献[8]的启发,结合CD方法,此处提出了一种修正的CD算法,该算法具有不依赖于所采用的线搜索方法的充分下降性;证明了该算法在Wolfe线搜索下的全局收敛性;通过数值试验验证了算法的有效性.
1 修正的CD算法


定理1设迭代方向由式(7)产生

若dTk-1yk-1≠0,则有



故定理1得证.
由定理1知,由式(7)产生的迭代方向均为下降方向,且该下降性的产生不依赖于任何线性搜索.
算法1MCD算法
步1给定初始点x1∈Rn,ε>0,d1=-g1,令k:=1;
步3由式(4)和式(5)求得αk;
步4计算xk+1=xk+αkdk,若,则算法停止,否则转步5;
步5利用式(6)计算βk+1,计算dk+1=-gk+1+βk+1dk,置k:=k+1,转步2.
2 算法的全局收敛性
下面,将在一定的假设条件下证明MCD算法的全局收敛性,如无特殊说明,下面的假设A总成立.
假设A
2)在水平集L1的一个邻域U内,f(x)是连续可微的,其梯度g(x)是lipschitz连续的,即存在常数L>0,使


证明由定理1及式(8)(9),可得

因此,
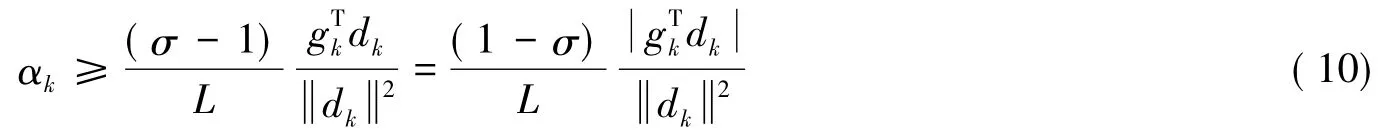
式(10)结合式(8)可得
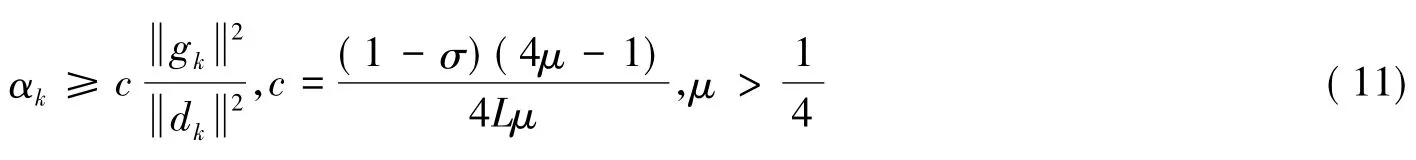
由式(4)和假设A,有

结合式(8)(12)和(13)可得条件Zoutendijk成立,定理1得证.

证明类似于文献[9],此处不再赘述.
3 数值试验
比较MCD与标准CD方法的性能,两种方法均采用Wolfe线搜索,试验中的函数全部来源于文献[9].测试环境为MATLAB 7.9.0,运行环境为内存4.00 GB,CPU为2.60 GHz的个人计算机.参数设置如下:δ=0.35, σ=0.75,0.25<μ<0.5;终止条件为或It-limit>9 999.计算得到2种方法的数值结果如表1所示.

表1 方法CD与MCD数值测试结果

注:“NI/NF/NG/Time”依次表示迭代的次数、函数值计算的次数、梯度值计算的次数和CPU运行总时间,“F”表示该方法失败.
通过以上简单数值试验,说明了新方法的可行性,但为了能得到更好的数值效果,还需要进一步研究方法中参数的选取和搜索条件的选择.
[1]FLETCHER R,REEVES C.Function Minimization by Conjugate Gradients[J].Computer Journal,1964(7):149-154
[2]POLAK E,RIBIERE G.Note Sur La Convergence De Dirctions Conjugees[J].Rev Fran-caise Informat Recherche Opertionelle,3e Annee,1969(16):35-43
[3]HESTEMES M R,SRIEFEL E L.Methods of Conjugate Gradient for Solving Linear Systems[J].Journal of Research of the National Bureau of Standards,1952,6(49):40-43
[4]FLETCHER R.Practical Methods Optimization[C]//Unconstrained optimization.New York:John Wiley&sons,1987
[5]LIU Y,STOREY C.Effcient Generalized Conjugate Gradient Algorithms[J].Journal of Optimiztion Theory and Applicatons,1991 (69):129-137
[6]DAI Y H,YUAN Y.A Nonlinear Conjugate Gradient with a Strong Global Conver-gence Property[J].SIAM Journal on Optimizton,2000(10):177-182
[7]敖卫斌.一种修正的DY共轭梯度法的全局收敛性[J].重庆工商大学学报:自然科学版,2013,30(10):17-20
[8]HAGER WILLIAM W,ZHANG HCH.A New Conjugate Gradient Method with Guaranteed Descent and an Efficient Line Search[J].SIAM Journal on Optimization,2005,16(1):170-92
[9]MORE J J,GARBOW B S,HILLSTROME K E.Testing Unconstrained Optimization Software[J].ACM Trans Math sofetware,1981 (7):17-41
A Sufficiently Descent CD Conjugate Gradient Method and Its Convergence
MA Shuo1,WANG An-ping2
(1.Jinzhou Vocational College of Technology,Hubei Jinzhou 434000,China; 2.School of Engineering and Technology,Yangtze River University,Hubei Jinzhou 434020,China)
Based on CD method,this paper proposes a modified CD conjugate gradient method(MCD method),the search direction generated by this algorithm is sufficiently descent direction and this property is nothing to do with the used line search method,and under certain condition,the solution to the global convergence of non-convex-optimization problem based on Wolfe line searching is proved.
unconstrained optimality;conjugate gradient method;Wolfe line searching;global convergence
O29
A
1672-058X(2015)01-0001-04
10.16055/j.issn.1672-058X.2015.0001.001
责任编辑:李翠薇
2014-05-29;
2014-06-10.
湖北省教育科学“十二五”规划课题(2012B310);长江大学工程技术学院基金(13J0802).
马烁(1981-),女,陕西蓝田人,讲师,硕士,从事最优化理论与算法研究.
**通讯作者:王安平(1980-),男,陕西旬阳人,讲师,硕士,从事最优化理论与算法研究.E-mail:wanganping2010@126.com.

