一类与Taylor展开有关的Bezout矩阵*

曹萌

(安徽大学数学科学学院，合肥 230601)

一类与Taylor展开有关的Bezout矩阵*

曹萌

(安徽大学数学科学学院，合肥 230601)

根据多项式的Taylor展开，首先给出了多项式对在基{1，x－a，…，(x－a)n－1}下的Bezout矩阵的表达式;其次得到了该Bezout矩阵中元素的一种具体算法;最后通过一个实例来加以说明.

Taylor展开;经典Bezout矩阵;Bernstein Bezout矩阵;算法

Bezout矩阵是由多项式对定义出的特殊方阵，是一种基础的研究工具.自18世纪引入以来，关于Bezout矩阵的研究受到了广大科研工作者们的高度重视，现已被广泛应用于控制论、多项式稳定性系统等领域中［1－2］.关于Bezout矩阵性质的研究，国内的研究者们对其做出过一些详细的探讨，给出了一些不错的性质，具体可参考文献［3－7］.文中第一节先回顾几个需要用到的定义;第二节给出了多项式对在基{1，x－a，…，(x－a)n－1}下的Bezout矩阵(f，g)的表达式;第三节提供了求解该Bezout矩阵(f，g)中元素的一种具体算法;最后一节中，通过所列举出的一个简单实例，对前面的定理给予验证说明.

1 预备知识

定义1［8，9］称线性空间P［x］n中n个线性无关的向量{1，x，…，xn－1}为多项式的标准幂基，为多项式的Bernstein基，其中

定义2［10］对于给定的多项式对

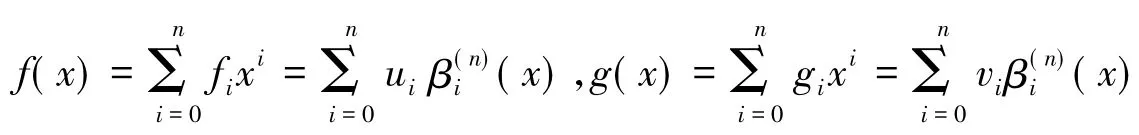
称由生成函数

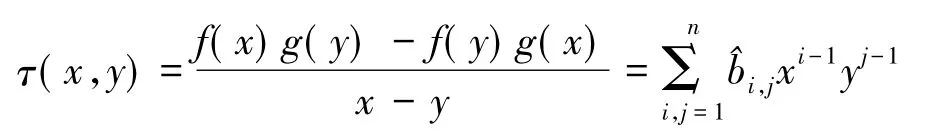
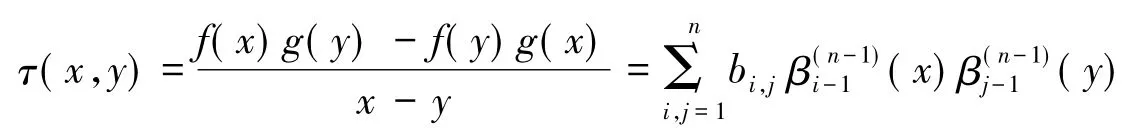
2 多项式对在基{1，x-a，…，(x-a)n-1}下Bezout矩阵的表达式

引理1［11］标准幂基{1，x，…，xn-1}和Bernstein基之间满足关系式

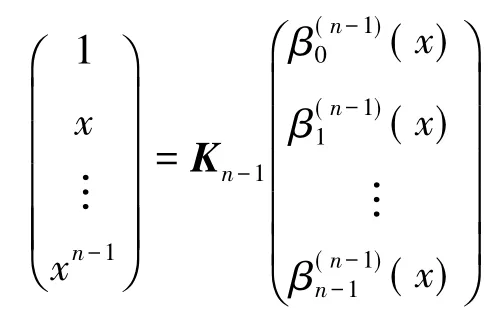
其中Kn-1＝(ki，j)ni，j＝1满足

证明容易得出

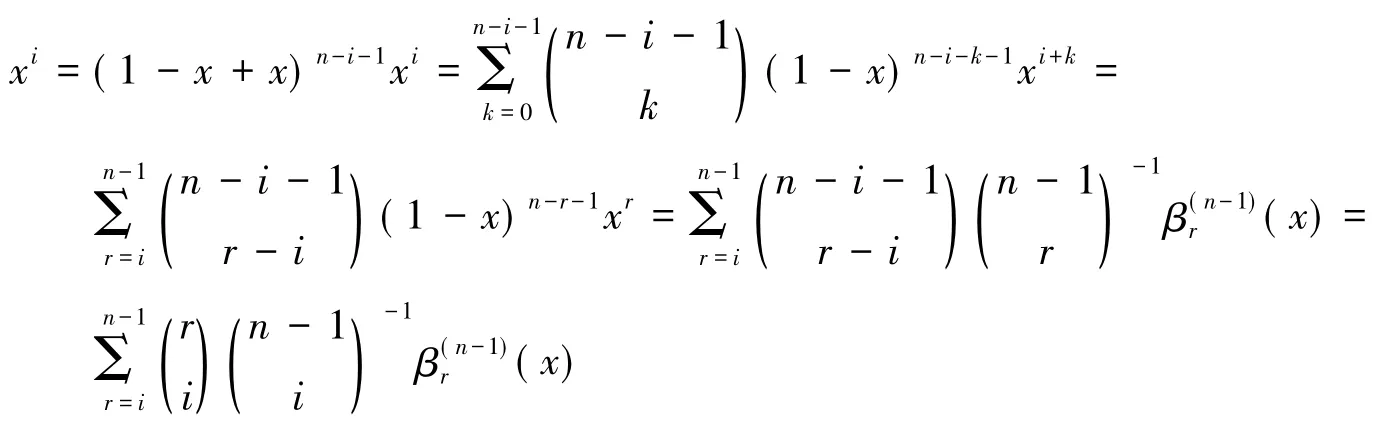
等号两边分别取i＝0，1，…，n-1，可知

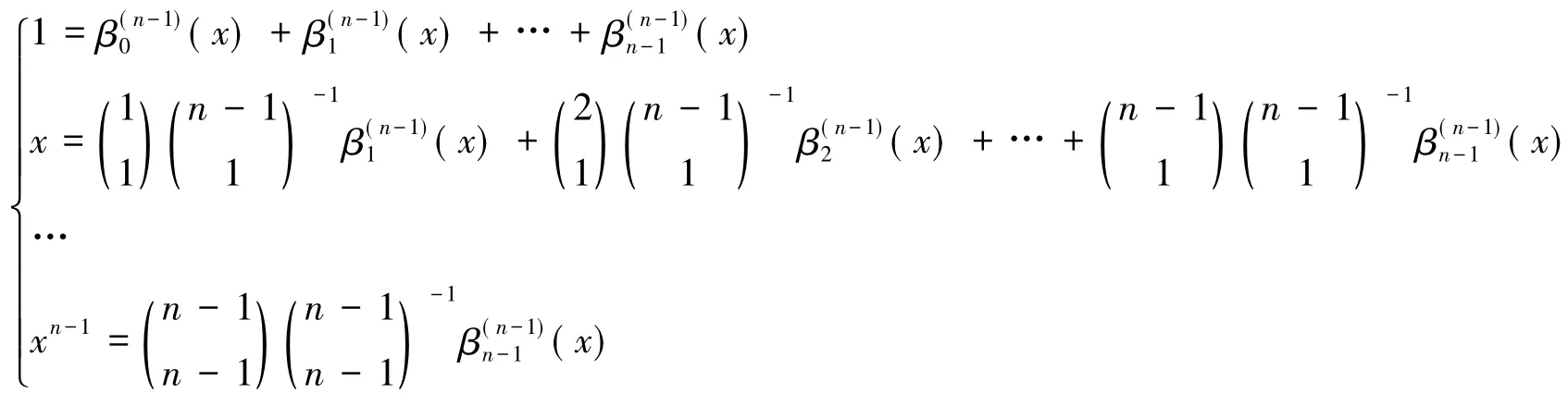
从而引理1成立，证毕.

定理1对于任意的成立，其中

称为标准幂基{1，x，…，xn-1}到基{1，x-a，…，(x-a)n-1}的过渡矩阵.

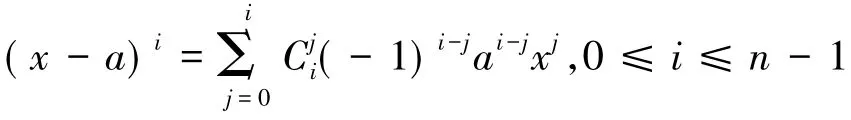
定理2设给定的多项式对

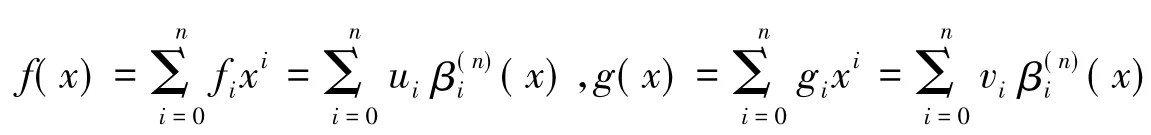
证明由题设条件和定义2，引理1以及定理1可知

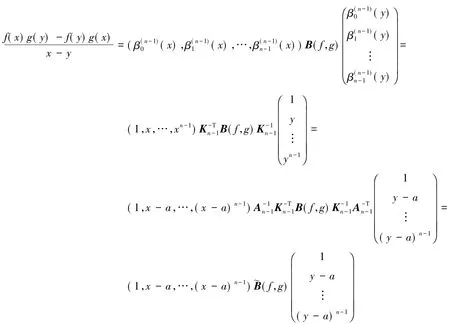
在这一节中，对f(x)和g(x)进行Taylor展开后，利用基本算数运算，给出了求解˜B(f，g)中元素的一种具体算法.

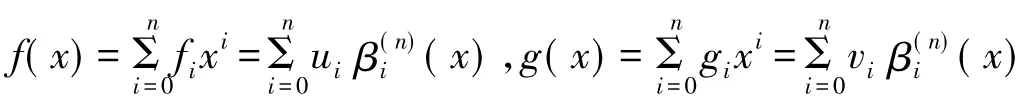
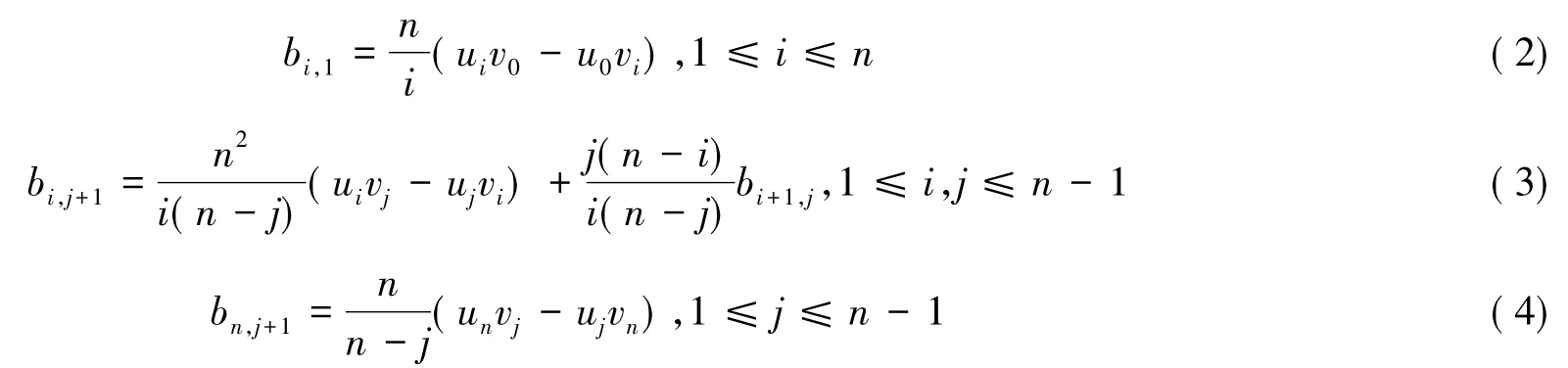
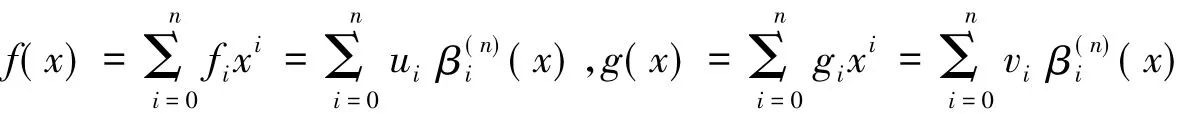
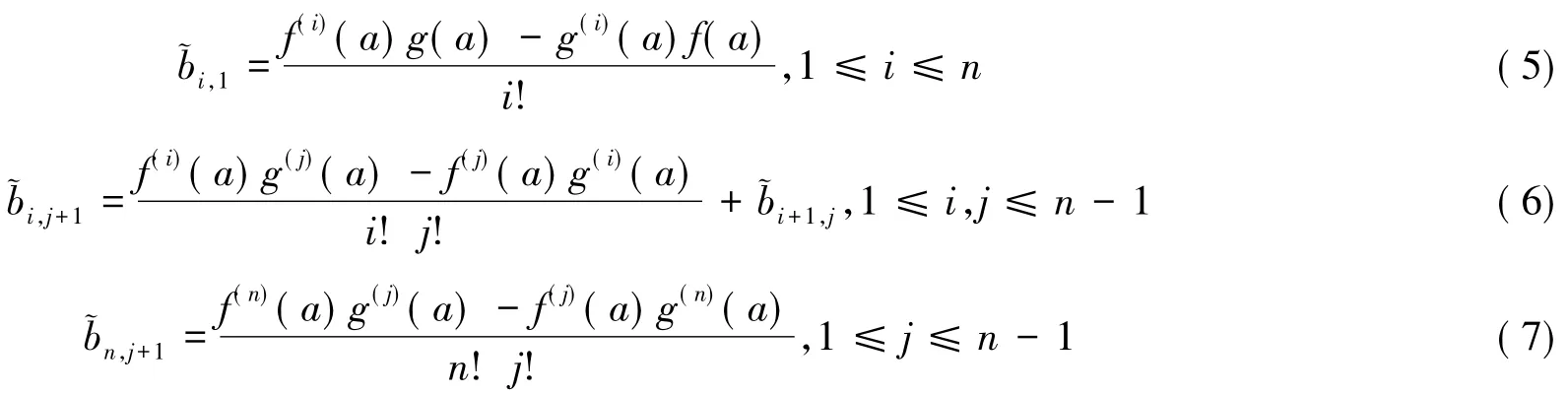
证明由题设条件可知

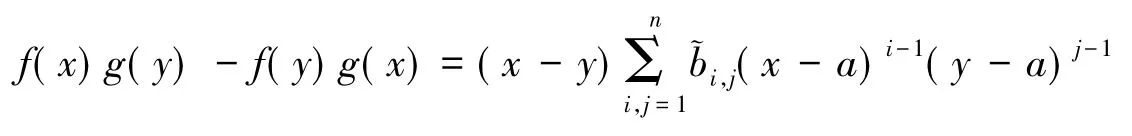
根据Taylor展开可知

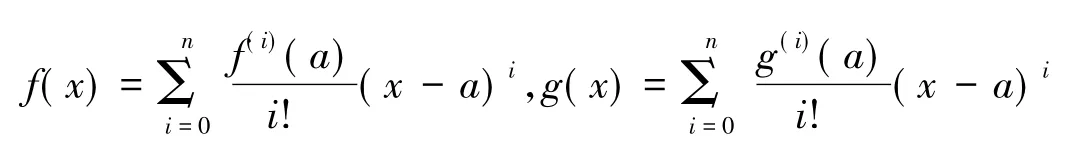
故有

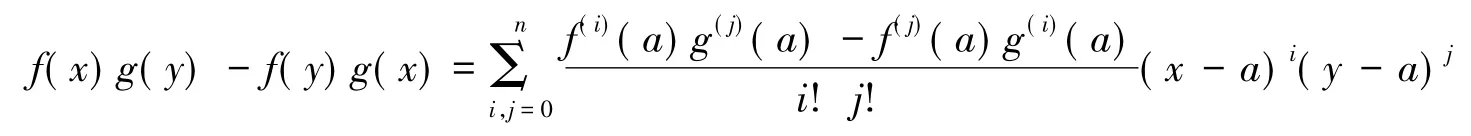
从而有

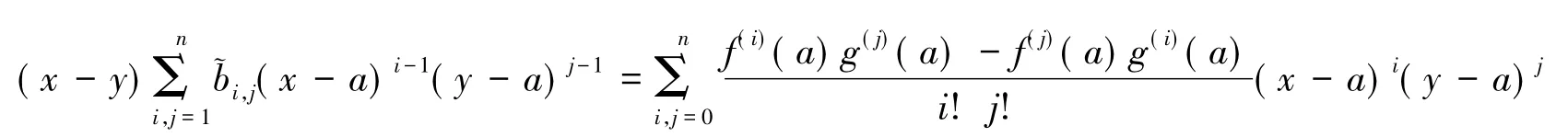
由于

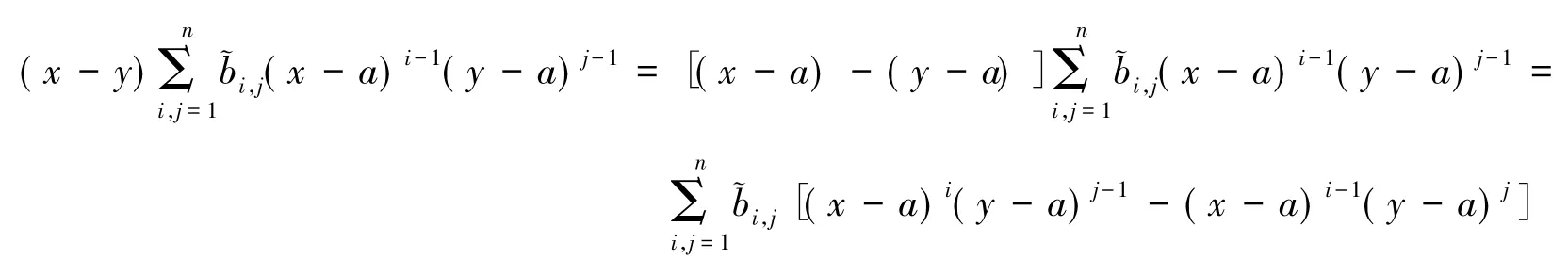
故有

分别比较式(8)等号两边(x-a)i，(x-a)i(y-a)j以及(x-a)n(y-a)j的系数可知

即得到式(5)(6)(7)，故定理3成立，证毕.

4 实例

在这一节，通过一个计算˜B(f，g)的简单实例，作为对前面定理的验证与说明.

例1给定多项式对

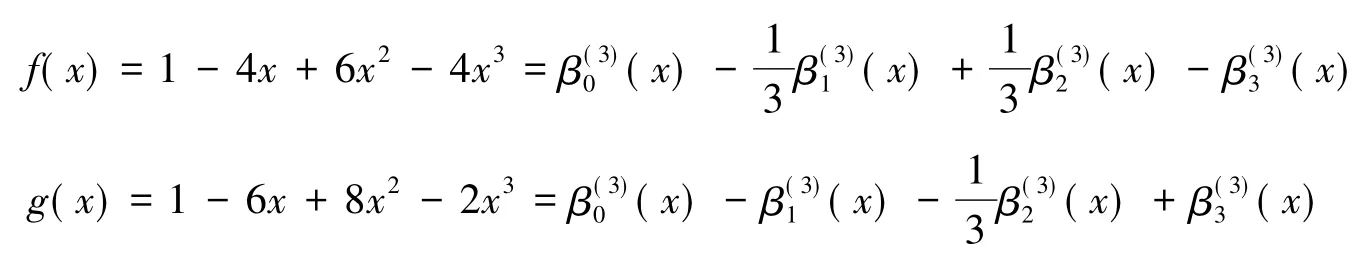
由式(2)可知

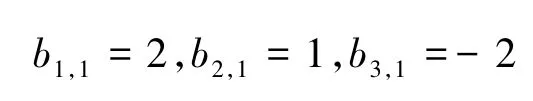
由式(3)可知

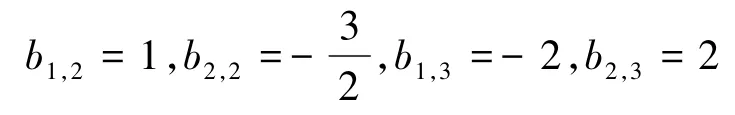
由式(4)可知

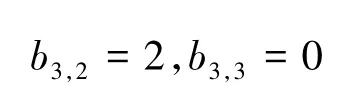
故有

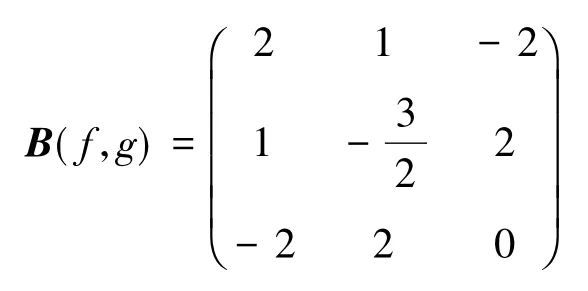
取a＝1，则有

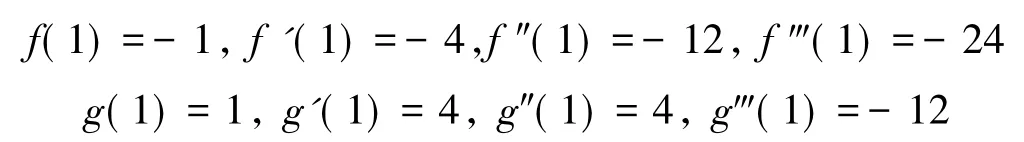
则由式(5)可知

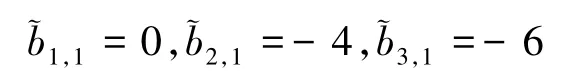
由式(6)可知

由式(7)可知

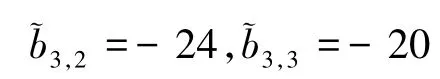
故有

此外易知

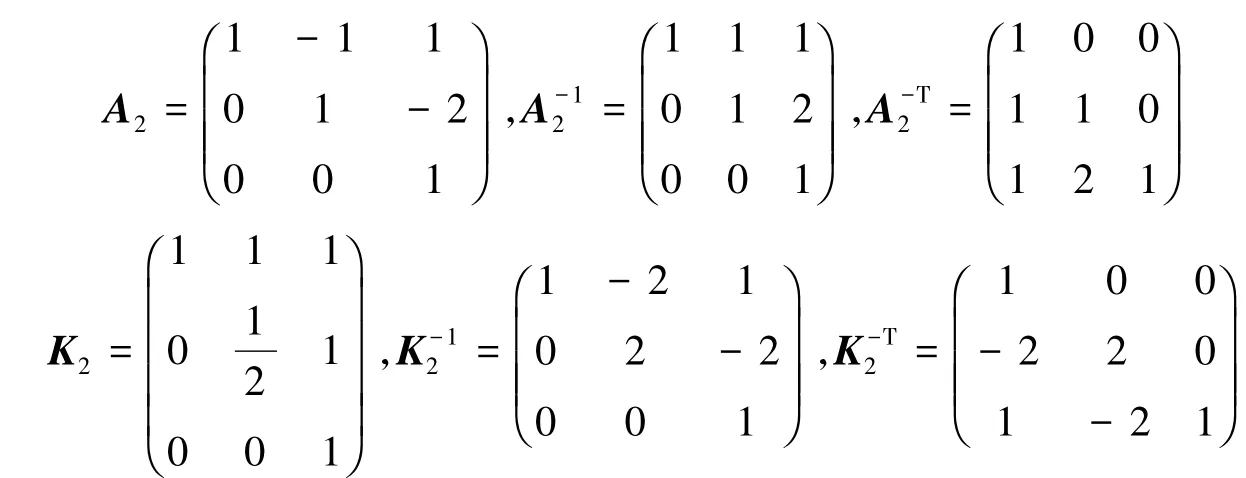
故由式(1)可知

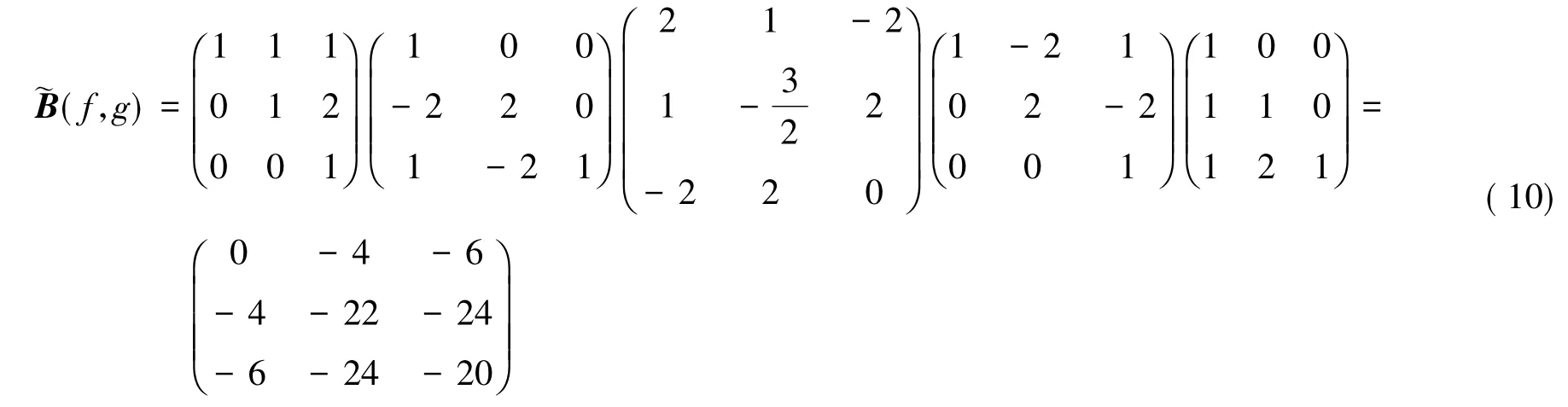
不难发现，式(9)(10)两式的结果是完全相同的，这也验证了定理2与定理3是等价的.

5 小结

将多项式与Taylor展开联系在一起，通过上面给出的简单实例，不仅可以反映出定理2用矩阵形式表示(f，g)的合理性，而且容易看出定理3提供的计算(f，g)中元素的这种具体算法是简便有效的.

［1］FUHRMANN P A.Polynomials Models and Algebraic Stability Criteria［M］.New York:Springer，1982

［2］BARNETT S.Polynomials and Linear Control Systems［M］.New York:Marcel Dekker Inc Press，1983

［3］杨正宏.Bezout矩阵与多项式稳定性判别法的一种新证明［J］.中国农业大学学报:自然科学版，1997，2(4):11－14

［4］梁燕来，杨正宏，陈公宁.关于一般多项式基的Bezout矩阵的若干性质［J］.北京师范大学学报:自然科学版，2003，39(1): 14－20

［5］刘冰，张羽乾.Bernstein－Bezoutian矩阵的若干性质［J］.重庆工商大学学报:自然科学版，2011，28(4):339－342

［6］王金凤，孙彬.对称矩阵与Bezout矩阵之间关系的探讨［J］.重庆工商大学学报:自然科学版，2011，28(5):467－469

［7］张战英，吴化璋.多项式Bezout矩阵束［J］.合肥工业大学学报:自然科学版，2012，35(4):563－566

［8］王萼芳，石生明.高等代数［M］.3版.北京:高等教育出版社，2003

［9］常庚哲，史济怀.数学分析教程(上册)［M］.北京:高等教育出版社，2003

［10］LANCASTER P，TISMENETSKY M.The Theory of Matrices with Applications［M］.2nd ed.New York:Academic，1985

［11］BINI D A，GEMIGNANI L.Bernstein－Bezoutian Matrices［J］.Theoretical Computer Science，2004(315):319－333

A Class of Bezout Matrix Related to Taylor Expansion

CAO Meng

(School of Mathematical Science，Anhui University，Hefei 230601，China)

According to polynomial Taylor expansion，this paper firstly gives the expression of Bezout matrix of the polynomials under the basis{1，x－α，…，(x－α)n－1}，then obtains a practical algorithm of the elements in this Bezout matrix and finally makes illustration by using an example.

Taylor expansion;classical Bezout Matrix;Bernstein－Bezout Matrix;algorithm

O151.21

A

1672－058X(2015)01－0005－06

10.16055/j.issn.1672－058X.2015.0001.002

责任编辑:李翠薇

2014－05－23;

2014－06－27.

安徽省自然科学基金资助项目(1208085MA02).

曹萌(1991－)，男，安徽六安人，硕士研究生，从事矩阵与算子理论、多项式与线性控制系统理论的研究.