气阀动力特征参数对活塞式压缩机示功图的影响*
钟幸宏,干 洪,何芝仙(安徽工程大学机械与汽车工程学院,安徽芜湖241000)
气阀动力特征参数对活塞式压缩机示功图的影响*
钟幸宏,干洪,何芝仙
(安徽工程大学机械与汽车工程学院,安徽芜湖241000)
摘要:在一定的假设条件下,建立往复式压缩机工作过程数学模型,编程求解并绘制出热力过程P-V示功图;研究了气阀动力特征参数对压力曲线的影响,并给出特定工作条件下气阀参数的最优组合;研究结果表明:吸气阶段,阀片质量越小,气缸最小压力升高,阀片开启时间越短,不易出现滞后启闭现象;弹簧刚度系数与最小压力及阀片启闭关系不显著,系数越大,曲轴转速越低,越易引发“颤振”现象;弹簧预压缩量越小,弹簧个数越少,愈易引起阀片滞后关闭,此外,弹簧刚度越大时,这种影响越显著。
关键词:活塞式压缩机示功图气阀特征参数热力过程
往复式压缩机工作过程仿真国内外已有大量研究[1-6],而计算机技术的发展使得仿真精度有了很大提高,所建模型及获得的示功图与试验结果较吻合。然而,现有文献中有关气阀动力特征参数对示功图的影响研究不多,而示功图已是研究压缩机故障诊断问题的有效手段[7-11]。压缩机示功图不仅与其工况参数有关,气阀动力特征参数对其影响也很大。因此,首先建立气缸热力过程数学模型,着重讨论气阀动力特征参数对压缩机示功图的影响,为后续研究压缩机主传动系统的动力学,流体力学等多学科耦合问题奠定基础。
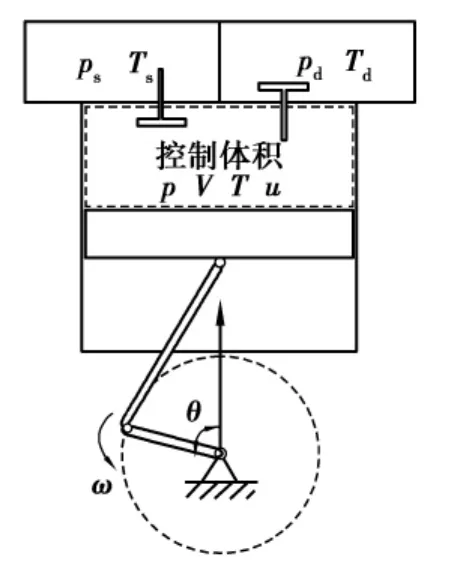
图1 气缸控制体
1 热力学理论基础
为了建立压缩机工作过程的数学模型,以压缩机气缸壁,活塞端面,缸盖形成的空间为控制容积,建立由气缸容积、进排气阀、泄漏间隙等组成的开口变质量热力系统,如图1所示。为简化问题,作如下假设:压缩工质为理想气体;气缸内任意两点气体的温度、压力、密度均相同,即气缸内热力工质是均匀的;任何外界作用可以及时传至气缸内所有质点;忽略流入或流出控制体积的气体的动能和位能;无气流脉动,进、排气腔压力保持不变;气体通过吸、排气阀过程视为一元稳定绝热流动;忽略泄漏造成的能量损失;曲轴旋转角速度ω为常数。因涉及较多符号,未做注释时以表1为准。

表1 符号说明

续表1
根据热力学的能量守恒定律及质量守恒定律,以及理想气体状态方程和容积方程,可以建立压缩机工作过程的数学模型。

1.1能量守恒方程据理想气体性质以及绝热假设,变形化简得到吸、排气过程能量方程的具体形式[5]:据假设,考虑热传递的压缩、膨胀过程其化简后能量方程为


1.2质量守恒方程

由于忽略泄漏,故控制容积内质量守恒方程为各阶段(吸气,排气,膨胀及压缩)质量方程为

2 数学模型的建立
2.1气体状态方程
假设气缸工质为理想气体,故状态方程: pV=mRT,压缩、膨胀过程为封闭系统等质量变化,因此上式对转角求取微分得:吸、排气过程为开口变质量系统,压力变化与阀片位移有关,故应建立阀片运动方程。

2.2阀片运动方程
以环状阀为研究对象,气阀阀片运动可简化为单自由度单质点运动,忽略气阀油粘力、摩擦力等的影响,阀片运动微分方程为

式(4)中: h为阀片位移。对于进气阀p1=ps,p2=pc;对于排气阀p1=pc,p2=pd。其初值为

阀片与阀座或升程限制器碰撞时,形成边界条件:当h=H,或h= 0时,其中: H为阀片升程,CR为反弹系数,取0.3;脚标reb为反弹值,imp为碰撞值。
2.3热交换方程
在压缩及膨胀过程中,以气体与气缸内壁对流换热为热交换的主要形式,忽略其他形式换热的影响,文献[10]给出了热交换方程:

2.4容积方程
往复式压缩机运动规律可用下列容积方程描述:

3 计算结果与讨论
3.1工作过程曲线
计算原始数据:活塞行程S = 11.4 cm,气缸直径D = 15.3 cm,相对余隙容积为5%,曲轴转速n=500 r/min,进气压力Ps=0.098 MPa,排气压力Pd=0.588 MPa,理想气体常数R=287.04 J/(kg×K),绝热指数k=1.4,气阀升程H=2.8 mm,压缩比ε=8。
将方程(2) -(6)代入能量方程(1),考虑到阀片运动方程是二阶常微分方程,可引入中间变量,因此,待求微分方程组构成了闭合的一阶常微分方程组。以活塞上止点作为初始点,假设名义排气状态参数为初值参数,应用四阶龙格库塔法(Runge-Kutta),逐阶段求解工作循环中各瞬时状态参数。分别绘制理想模型和综合考虑各种因素影响模型的两种情况下,压力曲线(图2)和示功图(图3)。计算步长取0.003 rad,阀片位移和速度初值取10-6。
压缩段热力曲线从起始上升至排气压力,活塞转角落后于理想模型若干相位,这是由于在压缩过程中,外界对气体做功,除了大部分转化为内能外,少部分以热能形式与气缸壁交换而损失。膨胀阶段同压缩阶段。排气阶段,当缸内气体压力与排气腔压力差值足以克服弹簧力时,排气阀才会开启,此时实际压力应大于名义排气压力。吸气阶段同排气阶段。

图2 压力与转角变化曲线

图3 P-V示功图
3.2曲线影响因素
缸内压力变化与气阀运动规律有着密切联系,而后者是气缸内压力,管路压力,气阀弹簧力,阀片开启高度,阀片重量等因素综合作用的结果。为了使结果更具代表性,将依次讨论阀片质量,弹簧刚度系数,弹簧预压缩量,弹簧个数,曲轴转速及阀片升程六个因素对压力变化的影响。又排气阀与进气阀情况相似,这里以进气阶段为例说明。
(1)阀片质量。取3组阀片质量绘制曲线如图4、5。当阀片质量不同时,其位移变化趋势呈现出显著差异。其中,阀片质量愈小,其与升程限制器及阀座碰撞次数越多,由此导致气缸内气压波动愈频繁。另外,质量越小,压力峰值越高,阀片开启所需时间越短,不易出现滞后启闭现象。

图4 阀片位移与转角

图5 气体压力与转角
(2)弹簧刚度系数。取3组刚度系数不同的弹簧绘制曲线如图6、7。当弹簧刚度较大时,阀片更易与升程限制器或阀座发生碰撞,在此期间,阀片将在阀座与升程限制器间作多次往返运动,即出现“颤振”现象。由图7可知,弹簧刚度不同并不会引起压力峰值的变化,刚度系数与阀片启闭时间长短关系不显著。
(3)弹簧预压缩量。针对两种不同刚度系数的阀片分别取3组预压缩量,绘制曲线如图8、9。其中,弹簧预压缩量越小,阀片停留在升程限制器上的时间延长,以致活塞到达止点位置时,阀片来不及落到阀座上,出现滞后关闭的现象。对比两图可知,在弹簧刚度不同的情况下,预压缩量对于上述现象影响程度有所差异,刚度愈大,预压缩量影响愈敏感。
(4)弹簧数量。针对两种不同刚度系数的阀片分别在3组弹簧数量情况下绘制阀片位移与转角关系曲线(图10、11)。据图可知,弹簧个数与预压缩量影响具有相似性。

图6 阀片位移与转角

图7 气体压力与转角

图8 阀片位移与转角(K=0.059 8 N/mm)
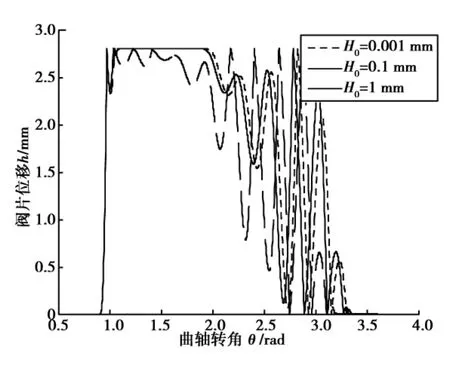
图9 阀片位移与转角(K=0.239 0 N/mm)
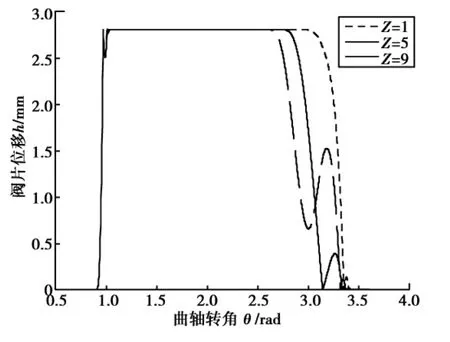
图10 阀片位移与转角(K=0.059 8 N/mm)
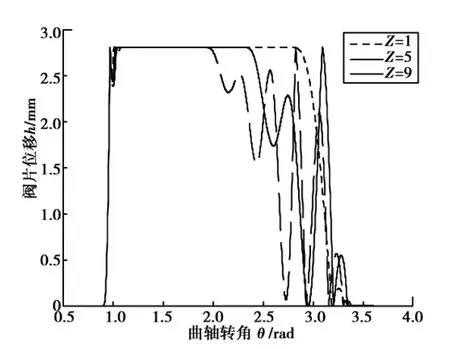
图11 阀片位移与转角(K=0.239 0 N/mm)
(5)曲轴转速。比较3组不同转速下的阀片位移及气缸压力变化曲线可知(图12、13),转速对于气阀启闭时间,压力峰值,以及阀片振动均有影响。转速越小,气体压力峰值越小,阀片开启越迅速,停留在升程限制器上的时间越短,不易出现滞后关闭现象。

图12 阀片位移与转角

图13 气体压力与转角
(6)阀片升程。取3组不同阀片升程绘制曲线图14、15。阀片升程对气体压力峰值及气压波动影响并不显著,相比之下,随着升程的增加,阀片开启的时间有所延迟。

图14 阀片位移与转角

图15 气体压力与转角
3.3因素组合优选
在给定工作环境下,引入压力最小值变量Pmin(MPa) (图15)描述吸气阶段阀片进入工作状态的快慢程度,Pmin越大则阀片开启越迅速。以阀片质量Mv和刚度系数K作为自变量,在给定区间Mv∈[0.002 47,247]及K∈[0.011 95,119 5]中,找出Pmin最大值及相应的最优匹配。
通过计算可知:当Mv取[0.002 5 0.012 4 0.025],并K取[0.012 0.059 8 0.119 5]时,上述9种组合方式的pmin最大,均接近于0.09 MPa(图16)。依此类推,找出吸气阶段pmin最大值所包含的最优参数组合:
(1) Mv=0.002 5 kg,K=0.012或0.059 8 N/mm,H0=0.00 1 mm,z=9,H=2.8 mm;
(2) Mv=0.012 4 kg,K=0.059 8 N/mm,H0=0.001 mm,z=9,H=2.8 mm;
(3) Mv=0.025 kg,K=0.059 8 N/mm,H0=0.001 mm,z=9,H=2.8 mm。
同理,排气阶段建立压力最大值变量Pmax(图17),并求出最小值及其最优匹配为Mv= 0.001 5 kg,K = 0.358 6 N/mm,H0=0.001 mm,z=9,H=2.8 mm。

图16 压力最小值分布

图17 不同阀片质量下排气压力曲线
4 结论
建立了压缩机气缸热力过程的数学模型,并利用计算机对其求解;分析了气阀特征参数对压缩机示功图压力变化的影响,并给出了特定工作条件下气阀特征参数的最优组合,为压缩机设计、故障诊断和研究压缩机多学科耦合问题奠定基础。
参考文献:
[1]郑超瑜,林匡行,周邵萍.基于MATLAB的往复压缩机气阀运动规律的仿真[J].压缩机技术,2005(2) : 41-43
[2]邢子文,徐勇良,束鹏程.活塞式压缩机工作过程的数学模拟和试验研究[J].流体工程,1986(12) : 1-8+65
[3]李强,王君,郑水英,等.往复压缩机压缩和膨胀热力过程研究[J].压缩机技术,2008(2) : 11-14
[4]林梅,孙嗣莹.活塞式压缩机原理[M].北京:机械工业出版社,1987
[5]郁永章.容积式压缩机技术手册[M].北京:机械工业出版社,2000
[6]PRAKASH R,SINGH R.Mathematical Modeling and Simulation of Refrigerating Compressors[J].International Compressor Engineering Conference,1974(2) : 132
[7]周蓉,梁荣光.通过汽油机性能参数确定示功图的方法研究[J].小型内燃机与摩托车,2009(4) : 31-36
[8]杨红,胡家顺,修吉平.基于PC的压缩机示功图测试、分析系统[J].压缩机技术,2003(3) : 14-16
[9]杨菲,苏永升.往复压缩机气阀故障诊断方法的试验研究[J].流体机械,2009(6) : 7-9
[10]高晶波,王日新,徐敏强.基于示功图修正的往复压缩机气阀故障诊断方法[J].压缩机技术,2009(3) : 4-8
[11]刘卫华,郁永章.往复压缩机故障示功图诊断法研究[J].压缩机技术,2001(6) : 9-12
Influence of Valve’s Dynamic Parameters on PV Diagram for
Reciprocating Compressor
ZHONG Xinghong,GAN Hong,HE Zhixian
(School of Mechanical and Automotive Engineering,Anhui Polytechnic University,Wuhu 241000,China)
Abstract:Under assumed conditions,a mathematical model of a reciprocating compressor working process is established,resolved by mathematical programming and the PV diagram is drawn.The influence of the valve’s dynamic parameters on the volume/pressure curve is analyzed,and the optimal combination of valve parameters under certain working conditions is presented in this paper.The research results reveal that a smaller valve mass results in a higher minimum pressure inside the cylinder during suction.The shorter valve opens,it’s more rare to delay opening and closing.Valve stiffness has little effect on the minimum pressure and the delay of valve opening and closing.The chattering phenomenon is more likely to occur with increasing stiffness coefficient and decreasing rotational speed.The delay time of valve closing is in inverse proportion to spring pre-compression and the number of valve spring,while being proportional to their stiffness coefficients.
Key words:reciprocating compressor; indicator diagram; valve characteristics parameters; thermodynamic process
中图分类号:TH101.1
文献标识码:A
文章编号:1672-058X(2015) 06-0079-07
doi:10.16055/j.issn.1672-058X.2015.0006.0016
收稿日期:2014-09-02;修回日期: 2014-10-24.
*基金项目:安徽省自然科学基金研究项目(1208085ME77).
作者简介:钟幸宏(1990-),男,安徽庐江人,硕士研究生,从事机械力学研究.

