模糊自适应PID控制在桥式起重机智能防摆中的应用*
胡艳丽,杨国诗,季学斌,刘团结(.淮南师范学院电气信息工程学院,安徽淮南3038; .神火集团大磨岭煤矿机电科,河南新密45370)
模糊自适应PID控制在桥式起重机智能防摆中的应用*
胡艳丽1,杨国诗1,季学斌2,刘团结1
(1.淮南师范学院电气信息工程学院,安徽淮南232038; 2.神火集团大磨岭煤矿机电科,河南新密452370)
摘要:针对桥式起重机模型的非线性和不确定性,在建立数学模型的基础上,完成了基于模糊自适应PID防摆控制器的设计;控制器在角度环和位置环分别采用了模糊控制器和模糊PID控制器,可对吊重摆角和小车定位进行有效地控制,提高起重机的工作效率;通过MATLAB/SIMULINK仿真证实方法的可行性,并且与常规PID控制进行比较,方法响应速度快,稳态精度高,而且对于不同的绳长和吊重质量方法具有较好的鲁棒性。
关键词:防摆;模糊PID;鲁棒性; MATLAB仿真
桥式起重机作为一种重要的物料搬运工具,广泛应用在车间、仓库、电厂等领域,是使用范围最广的一种起重机械。起重机吊重和小车之间采用柔性钢绳进行连接,作业过程中受到风力、摩擦及小车加减速等影响,会产生吊重的摆动。这种摆动会降低起重机的定位精度和稳定性,使起重机工作效率降低,而且严重时会发生一定的人身安全生隐患。近年来,很多学者采用增益调节、Lyapunov稳定理论、状态反馈、线性二次型最优控制(LQR)等方法在起重机防摆和小车定位方面做了大量研究[1,2],但这些方法对起重机系统数学模型的依赖性比较强。此处设计了一种基于模糊PID的智能防摆控制器,并对此控制方法在SIMULINK中进行仿真,和常规PID仿真结果进行比较,分析改进方法的优越性。
1 桥式起重机防摆控制系统建模
为了对桥式起重机防摆系统进行分析,首先要建立吊重系统数学模型,如图1所示。在建模时,考虑桥式起重机大车静止不动,利用拉格朗日方程建立吊重和小车运行时的二维振动模型。

其中,g为重力加速度,小车质量为M,吊重质量为m,绳长为l,吊重相对竖直线的摆角为θ,小车位移记为x,小车驱动力为F,钢丝绳起升力为Fl。
为了研究方便,假设钢丝绳定滑轮半径为一个悬挂点,同时忽略垂直方向的绳长变化和钢丝绳质量,即有。一般情况下,起重机在安全操作时,吊重相对竖线的摆角在操作点附近变化很小,即可认为θ≈0。所以可以假定cos θ=1,sin θ=0,则桥式起重机防摆系统模型可以简化为

对系统模型式(2)进行分析[3],可以发现大小车运行的加、减速度对吊重的摆角影响比较明显。
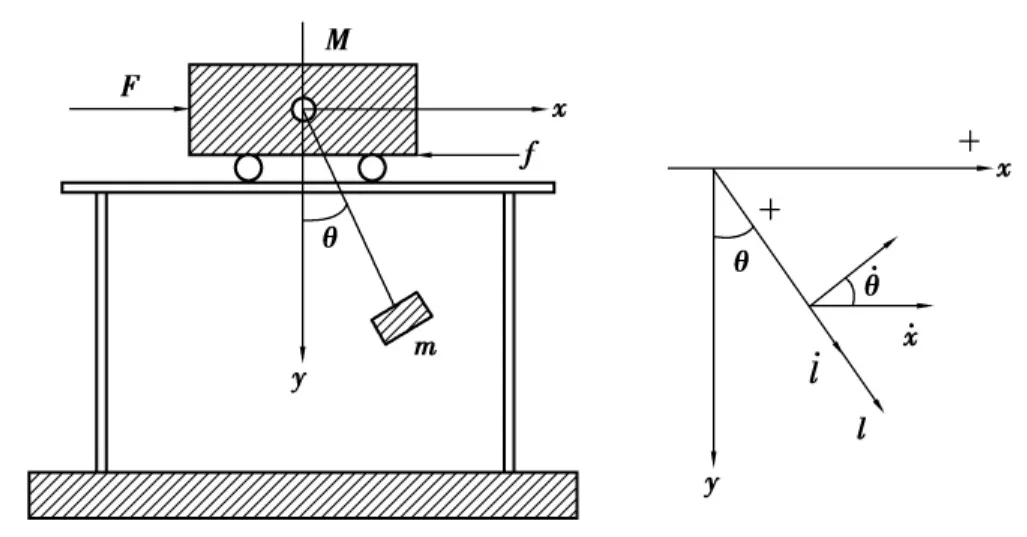
图1 桥式起重机小车运行系统模型
2 桥式起重机常规PID控制器设计与仿真
常规PID(比例-积分-微分)控制器具有使用灵活、应用广泛、稳定性强等优点。PID模块的传递函数为

由式(3)可知,控制器的控制效果取决的kp,ki,kd3个参数的整定。
根据防摆系统模型分析,桥式起重机防摆系统应包含两个PID控制器,外环PID1模块为小车位置控制器,确保小车能准确地停在指定位置;内环PID2模块为吊重摆角控制器,确保吊重摆角能迅速衰减到零或者规定的范围,图2中a代表系统的输出向量摆角θ。在SIMULINK[4]中建立起重机防摆常规PID仿真模块,如图2所示。
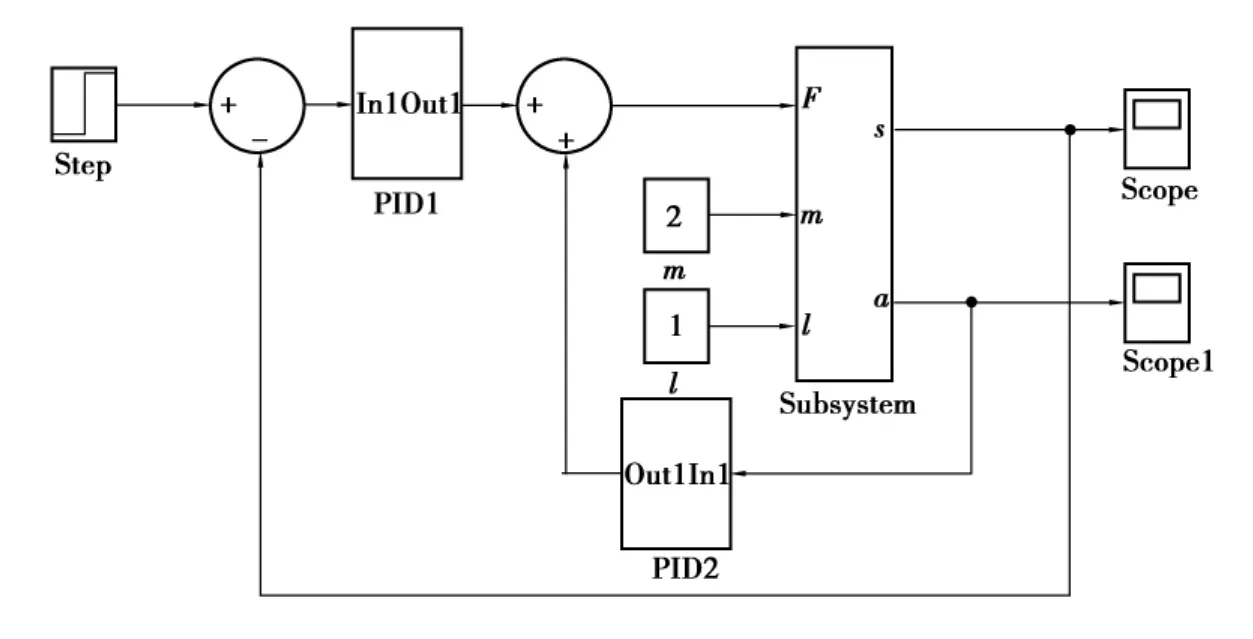
图2 起重机防摆系统常规PID控制仿真图
通过整定参数并仿真,得其阶跃响应曲线如图3所示。由图3仿真结果分析,常规PID防摆控制器位置调整时间在18 s左右,而且超调较大;刚开始运行时摆幅较大,摆角回到零位的时间在20 s左右,容易引发安全事故。

图3 常规PID控制仿真结果
3 起重机模糊自整定PID防摆控制器设计与仿真
3.1模糊自整定PID控制策略
此处设计的模糊PID[5]控制器输入变量为偏差e和偏差变化率ec,输出变量为KP,KI,KD;定义KP,KI,KD3个参数的调整算式如下

式(4)中,PID控制器的3个控制参数分别为KP,KI,KD;ΔKP,ΔKI,ΔKD为修正参数。采用常规方法可以得到预整定参数为K'P,K'I,K'D。对系统进行线控制时,系统的偏差e和ec要不断进行检测,然后将其模糊化可以得到E和EC。
3.2模糊控制规则
模糊控制规则的建立常用的方法往往是根据专家的经验和控制工程知识以及操作人员的实际控制过程,两者结合起来可以很方便的建立控制规则库。此处根据反复仿真试验结果和起重机司机的实际操作经验设计小车位置模糊PID控制器和吊重摆角模糊控制器。采用“if…then…”形式制定的KP,KI,KD的模糊控制规则和吊重摆角模糊控制规则分别如表1、2所示。

表1 小车位置模糊PID控制规则
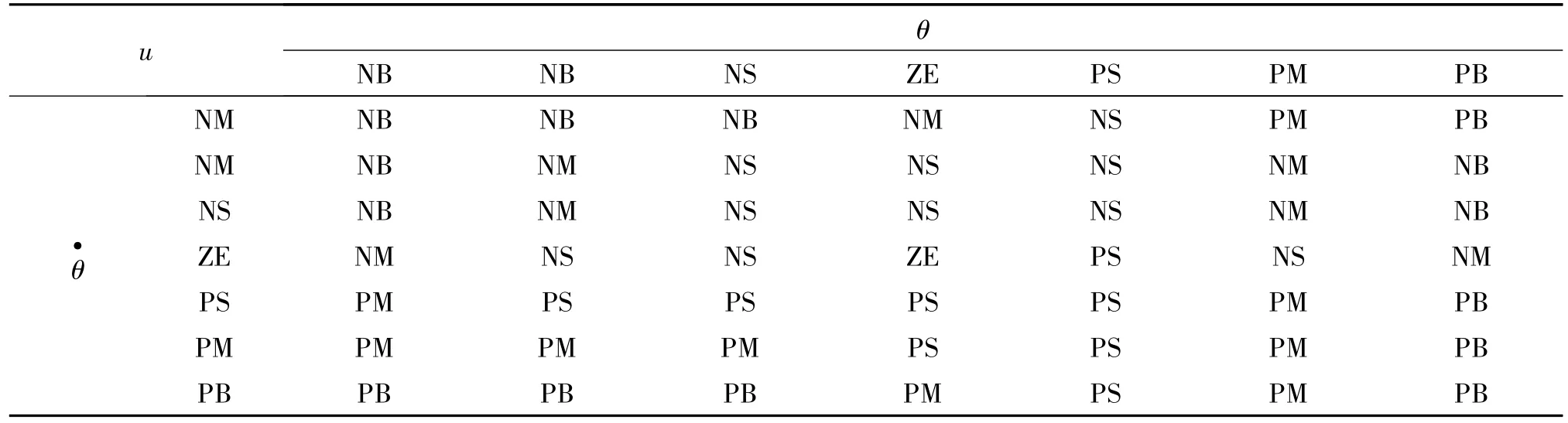
表2 摆角模糊控制规则
3.3桥式起重机模糊PID防摆系统仿真
在以上设计基础上运用MATLAB/SIMULINK进行仿真[7],可以得到绳长和吊物质量发生改变时的一组模糊PID控制器的仿真曲线如下:图4、5、6分别为不同的绳长和吊重的位置和摆角响应曲线。

图4 l=1.5 m,m=6 kg模糊PID防摆系统仿真结果

图5 l=1.5 m,m=12 kg模糊PID防摆系统仿真结果

图6 l=3 m,m=6 kg模糊PID防摆系统仿真结果
3.4仿真分析
图4、5、6的仿真结果与图3对比可知,采用模糊PID控制器所组成的防摆系统相对常规PID控制器使负载的摆动幅值减小,而且可以迅速消除摆动。起重机小车回到目标位置的响应时间缩短10 s左右,可以大大减小生产安全隐患。
4 结语
在对桥式起重机防摆系统建模的基础上,针对常规PID防摆控制器存在的不足,改进设计了模糊自整定PID防摆控制器,并对两种控制器在MATLAB/SIMULNK环境中分别进行仿真。仿真结果表明,两个控制器均能实现小车准确定位,并能消除吊物摆动,但模糊PID控制器使小车稳定时间缩短,吊重回零位超调减小。图4是绳长l=1.5 m,吊重质量m=6 kg时位置和摆角仿真曲线;图5是保持绳长不变,把吊重质量增加到12 kg时的位置和摆角仿真曲线;图6是保持吊重质量不变,把绳长增加到3 m时的位置和摆角仿真曲线。图5、6分别和图4进行对比,当吊重质量和绳长发生改变时,系统的鲁棒性仍然较好,可见改进后的防摆系统具有较大的优越性。
参考文献:
[1]蒋理,陈树广.基于模糊控制的桥式起重机定位防摆研究[J].计算机仿真,2009,26(6) : 179-182
[2]王克琦.桥式起重机的定位和防摆控制研究[J].系统仿真学报,2007,19(8) : 1799-1802
[3]曾光奇,胡均安,王东.模糊控制理论与工程应用[M].武汉:华中科技大学出版社,2006
[4]薛定宇,陈阳泉.基于MATLAB/Simulink的系统仿真技术与应用[M].北京:清华大学出版社,2003
[5]李祖松,陈其工,魏利胜.一类广义系统的开闭环PID型迭代学习控制[J].重庆工商大学学报:自然科学版,2012,29 (11) : 1-5
[6]BENHIDJEB A,GISSINGER G L.Fuzzy Control of Overhead Crane Performance Comparisons with Classic Control[J].Control Engineering Practice,1995,3(12) : 1687-1696
[7]王正林,王胜开,陈国顺.MATLAB/Simulink与控制系统仿真[M].北京:电子工业出版社,2005
Application of fuzzy self-tuning PID control in intelligent anti-Swing
control of bridge crane
Hu Yan-li1,Yang Guo-shi1,Ji Xue-bin2,Liu Tuan-jie1
(1.School of Electrical&Information Engineering,Huainan Normal University,Huainan 232038,China; 2.Electrical Department,Damoling Mine of Shenhuo Grope,Xinmi 452370,China.)
Abstract:For nonlinearity and uncertainty of bridge crane model,this paper designs a fuzzy self-tuning PID anti-swing controller based on the mathematical model.In the controller,fuzzy controller in the angle loop and fuzzy PID controller in the position loop are used,which can effectively control hoist swing and trolley position,to improve working efficiency of the crane.The MATLAB/SIMULINK simulation shows that the method is feasible.Compared with the conventional PID control,this method has fast response,high steady-state accuracy.and has better robustness for different hoist rope length and mass.
Key words:Anti-swing control; Fuzzy PID; robustness; MATLAB simulation
中图分类号:TP273
文献标识码:A
文章编号:1672-058X(2015) 06-0060-05
doi:10.16055/j.issn.1672-058X.2015.0006.0012
收稿日期:2014-08-05;修回日期: 2014-09-25.
*基金项目:2012年淮南师范学院科学研究项目(2012LK12).
作者简介:胡艳丽(1982-),女,安徽砀山人,硕士研究生,从事智能控制与信息处理技术研究.

