基于流型结构构造的混合设备优化设计方法

刘春江，赵明恩，郭 凯，齐文哲，黄哲庆，刘伯潭

(1. 天津大学化工学院，天津 300072；2. 化学工程联合国家重点实验室(天津大学)，天津 300072)

基于流型结构构造的混合设备优化设计方法

刘春江1,2，赵明恩1,2，郭 凯1,2，齐文哲1,2，黄哲庆1,2，刘伯潭1,2

(1. 天津大学化工学院，天津 300072；2. 化学工程联合国家重点实验室(天津大学)，天津 300072)

针对混合过程强化，提出一种基于流型结构构造的混合设备设计方法，即通过构造特定的流型结构达到强化混合的目的．该方法提出以混合过程的熵产作为目标函数，通过变分法构造拉格朗日乘子方程，最终得到熵产达到极值时的流型结构．模拟结果表明所构造的流型结构能有效强化混合过程．为了验证该方法的实用性，以烟气脱硝过程中的氨气/空气混合过程为例，利用该方法得到能够强化混合过程的特定流型结构．最后利用所得到的流型结构，借助多孔介质模型设计出具有内部结构的混合器．

混合过程强化；流型结构构造；变分法；设备优化设计

设备的优化设计是实现化工过程强化的有效手段之一．传统的化工设备优化设计往往依赖于设计者的经验，优化的思路往往是针对现有的结构提出几种可能的优化方案，再根据实验或数值计算的方法对不同的方案进行对比，从中选出最优的结构．而不同的设计者由于经验背景的差异会提出不同的优化方案，因此这种传统的设备优化思路往往缺乏理论基础，不具有普遍的可操作性．因此建立一种普适的化工设备优化方法，是目前化学工程领域尚未完全解决的基础性问题．

针对上述问题，许多研究者进行了有益的尝试.其中，从热力学角度出发进行传递过程的强化已经取得了广泛的应用．Bejan[1-5]指出在对流传热过程中，热量传递以及流动阻力会引起系统的不可逆性．通过降低系统的熵产，可以有效地减小系统的不可逆程度．Bejan将熵产最小原则应用于对流换热过程的优化以及相关设备的设计．1987年，San等[6]通过热力学第二定律分析得到热质传递过程中由于传热、传质及流动阻力造成的熵产表达式，并以具有代表性的二维平板流动为例，分别对层流以及湍流中的熵产进行了优化，得到了最佳的板间距．1991年，Carrington等[7]从非平衡热力学的角度对热质传递过程进行了讨论，同样得到了由于过程不可逆性而造成的熵产表达式，并分析了熵产产生原因．之后，Yao[8]得到了局部热力学平衡时热质传递过程的熵产表达式，并将其应用于内流和外流的熵产分析中，得到了传递过程中由于热质传递以及流动阻力造成的熵产表达式，并通过优化操作条件达到降低熵产的效果．除此之外，许多研究者也提出过基于不同原则的设备优化方法．20世纪90年代末，Bejan等[9-10]根据自然界生物形态演化规律提出了构型理论，其理论可表述为对于一个沿时间箭头方向(或为适应生存环境)进行结构演化的流动系统来讲，为流过其内部的“流”提供越来越容易通过的路径是决定其结构形成的根本原因．构型理论从自然进化的角度阐述了设备结构优化思路，在相关设备结构的优化设计中取得了显著的成果[11-15]．法国 Savoie大学罗灵爱教授领导的课题组从设备结构优化的角度出发，开展了一系列的研究工作，提出了很多设备结构优化准则：Luo等[16-17]使用格子气自动机法，对导热过程中常见的“面-点”以及“点-点”问题进行了优化，得到了有利于导热过程进行的枝型结构(tree-network configuration). Wang等[18]提出流动优化中的自演化机制，并使用LBM 方法优化了流体流经管道时的压降，得到了有利于流动的流道结构．此外，清华大学过增元院士领导的课题组从场协同的角度出发，通过改善不同物理场之间的协同效应实现传递过程的优化．Guo等[19]将导热过程与导电过程进行对比，提出了火积(entransy)的概念描述传热能力，指出火积的耗散代表了传热能力的降低，并将耗散极值原则用于传热过程的优化．Chen等[20-21]提出质量积(mass entransy)的概念描述传质能力，并将耗散极值原则用于对流传质过程的优化．

基于前人所做的工作，本课题组提出基于特定流型结构构造的传递过程强化以及相关设备的优化设计思路．作为该方法的初步探索，笔者主要针对气体混合过程的强化对相关设备的优化设计进行了研究.

1 模型建立

热力学第二定律揭示由于过程的不可逆性会造成有用功的损失，表现为系统的熵产．那么，从热力学角度上讲，降低系统熵产可以降低有用功的损失，这是一种行之有效的提高热力学效率的方法．系统的熵产是与系统内部的流动方式以及热量传递过程密切相关，通过优化设备结构改变流动以及传热方式，降低系统的熵产，从而提高换热效果．

本文尝试将熵产寻优方法应用于混合过程优化中，以熵产为目标函数，在一定约束条件下推导出熵产极值的必要条件，并通过添加体积力来改变流型结构，使熵产达到极值．

1.1 对流传质系统中的熵产

不可压缩牛顿流体单位体积的熵产[22]为

式中：i、j为速度方向；下标“α”为组分．式(1)中右边第1项是由于流动阻力产生的熵产；第2项和第3项分别是由于质量扩散和热量扩散产生的熵产；第 4项是由于热质传递的相互作用引起的熵产；第5项是由于化学反应产生的熵产．

本文不涉及到化学反应，假设对流传质过程为等温过程，可以忽略传热过程造成的熵产．因此，式(1)简化为

式中：μα°为纯组分α在温度 T时标况下的化学势；pα为组分α的分压．根据理想气体状态方程可知

理想气体混合物中任意组分的化学势为

根据Fick定律，传质通量表示为

由于质量扩散引起的熵产表示为

根据伯努利方程，对于流体系统机械能的损失，或者说主要的流体压降是由流体之间的剪应力造成的，而这也会导致系统熵产，即流动阻力熵产．

1.2 对流传质过程的数学模型

对传质过程进行以下假设：

(1) 混合过程在常压下进行，气体混合物视为不可压缩理想气体混合物；

(2) 忽略密度差引起的对流过程，气体混合物视为均质混合物；

(3) 不考虑温度的影响．

基于以上假设，氨气/空气二元混合物的熵产为

稳态层流下，混合过程可以由连续性方程、组分输运方程以及运动方程描述，即

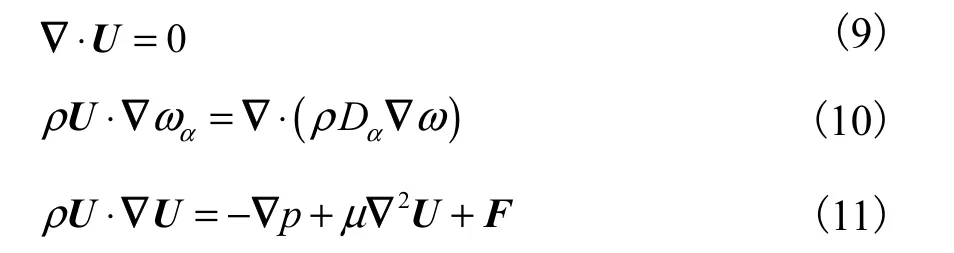
熵产寻优目标需通过改变混合器内部流场来实现，本文通过体积力F来改变流场，进而实现使熵产取极值的目标．

1.3 流型结构优化

通过改变速度场而提高系统的传热传质效率是一种行之有效的方法[23-27]．相比于原始流场，在特定的流型结构中传递过程得到强化的同时也会带来诸如压降升高、机械能损失增加等问题．这些负面影响可以视为过程强化的“代价”．在不同的熵产下，系统的混合程度是不同的．因此，优化模型的建立应以调整系统熵产为目的．但是对于一个具体的实际应用来讲，往往需要控制过程的机械能输入或者压降在一定的范围内，这样才具有应用的意义．为此，将式(8)中由于流动阻力产生的不可逆性视为约束条件而不再是优化目标．因此以黏性耗散函数定量描述流动阻力造成的影响．不可压缩流体的黏性耗散函数表示为

混合过程的强化可以描述为：在约束条件下(连续性方程、组分输运方程以及一定的黏性耗散值)构造特定的流型结构，调整系统熵产．由扩散而造成的熵产能反映扩散进行的程度，因此在不同的传递机制下可以通过调整熵产达到强化传递的效果．在以扩散为主导的传递过程中，增大熵产意味着扩散过程得到强化；而在以对流为主导的传递过程中，降低熵产意味着对流过程促进传质从而抑制由浓度梯度引起的扩散．因此基于熵产分析的混合过程强化是典型的变分问题．

构造相应的拉格朗日乘子方程为

压降的约束表示为

式中 C1、C2和 C3为拉格朗日乘子．约束条件的类型不同，C1和 C2为位置函数，C3为常数．

方程(13)对质量分数求变分，得

方程(13)对速度求变分，得

根据文献[20，23，28]报道，乘子 C1与压力 p满足函数关系 C1＝－2C3,p，因此式(15)化为动量方程形式为

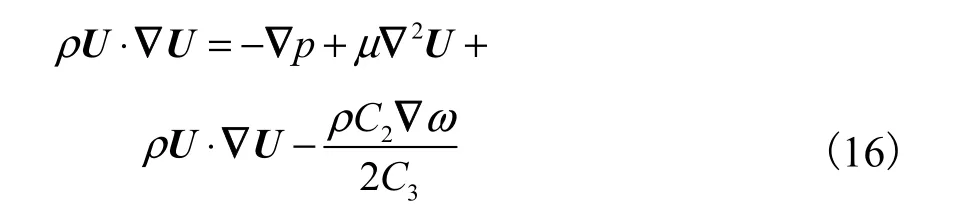
对比方程(11)和(16)，可得虚拟体积力表达式为

至此，得到了优化流场的控制方程组，包含连续性方程(9)、组分输运方程(10)、运动方程(11)、(17)以及乘子方程(13)．通过求解该方程组，可改变流型结构，得到熵产极值时的流场．

乘子 C2由方程(14)的计算得到；在变分法中积分约束条件的乘子为常数，因此乘子C3为一常数，且对应于一定的黏性耗散值．也可以说，一定的黏性耗散值映射一个 C3值．C3的取值根据具体问题而定，笔者通过尝试不同的 C3值从而确定一个合理的范围，这个范围取值有一定原则，通常不能大于过程所能接受的黏性耗散值(压降)．从笔者的计算结果以及文献[23，26]的报道中可知，不合理的 C3赋值会有两种结果：一种是流场异常混乱以致无法得到收敛的数值解；另外一种就是施加的作用力对于流场的影响很小可以忽略．这两种情况对于流场的优化是没有帮助的，因此本文通过计算不同 C3值对应的优化流场，得到 C3的合理取值范围．在该范围内，既能得到收敛的数值解也能保证优化效果．

2 混合过程的优化

2.1 物理模型

为了节省计算资源，将管式混合器的某一中心截面作为计算模型．图 1为气体混合器的二维物理模型，长度和高度分别为6,cm和1,cm．进口分为3部分，中间为氨气进口，上下分别为含氨气质量分数为1%的空气进口．为了避免进口和出口影响混合过程的强化，将混合器的中间区域作为优化区域，优化区域距离进口1,cm，总长度为2,cm．

图1 物理模型Fig.1 Sketch of the physical model

混合过程操作温度恒定为 293,K，操作压力为常压．混合物的密度恒定为进料组成下的平均密度，黏度为 1.79×10-5,Pa·s，氨气在空气中的扩散系数为1.978×10-5,m2/s[27]，经过计算Re在层流范围内．

2.2 边界条件

入口边界条件：速度入口

出口边界条件：压力出口

壁面边界条件：采用无滑脱边壁条件

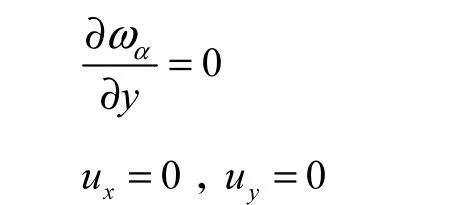
2.3 模型验证

首先根据物理模型建立计算模型．采用 Fluent 6.3.26进行数值计算，速度和压力离散方程组采用SIMPLE算法求解，离散过程的对流项和扩散项采用QUICK差分格式．

网格数对数值模拟至关重要，合理的网格数目能使模拟计算快速而准确．本文划分了数目为 38,400、60,000、101,400、173,400、240,000和317,400 6种网格，并计算了同一雷诺数、不同网格数下的流场以及浓度场．计算结果表明，当网格数目大于 173,400时，流场、浓度场以及出口处的离析度[29](intensity of segregation，IOS)保持恒定．本文选取 1,200×200 (长×高)共 240,000个网格划分策略，该网格密度能保证模型结果的可靠性．

使用离析度定量评价混合均匀程度，即

2.4 混合过程的优化

原始流场氨气的质量分数分布及流线图如图 2所示，出口处的IOS为0.153,84．由于缺少y方向的速度分量导致流体层之间没有相对运动，混合效果不佳．

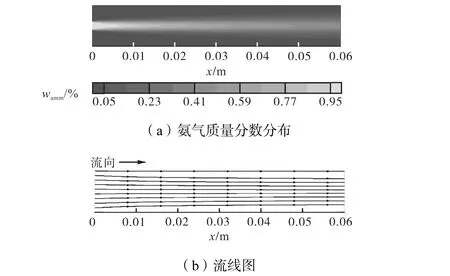
图2 原始流场中氨气质量分数分布及流线图Fig.2 Contours of mass fraction of ammonia and streamlines in the original flow pattern

加入虚拟体积力F后，流场发生改变．优化后的氨气质量分数、速度分布及流线图如图 3所示，出口处的IOS降低到0.012,67．计算结果证实，在优化流场中由于虚拟体积力 F，构造了特定的流型结构，加剧了流体层之间的相互混合．但是特定的流型结构也消耗了更多的机械能．为考察乘子 C3对于混合效果的影响，进行了参数灵敏度分析，通过改变C3的数值得到不同黏性耗散下的优化流场．如图 4所示，随着 C3的增加，黏性耗散逐渐增加，离析度逐渐降低．优化之后，压降从 0.235,3,Pa提高到27.629,7,Pa．作为混合强化的代价，机械能损失的增加，或者说是压降的增大是不可避免的．

图3 优化流场中速度分布、氨气质量分数分布及流线图Fig.3 Contours of velocity magnitude，mass fraction of ammonia and streamlines in the optimized flow pattern

图4 黏性耗散以及离析度随拉格朗日乘子的变化曲线Fig.4 Variations of the viscous dissipation rate and the intensity of segregation with Lagrange multiplier

3 混合器结构优化

由上述结果可知，通过构造特定流型能改善混合效果，该优化流场对混合器设计具有指导意义．本节基于优化流场，引入多孔介质模型对混合器的结构进行改造，以强化混合过程，实现熵产寻优的目标．

由于多孔介质产生的动量源相为

式中：C为模型参数；α 为多孔介质的孔隙率．

层流流动中，相比于黏性阻力项，层流惯性项可忽略．因此，式(19)简化为

固体物质认为是 α= 0的多孔介质．从式(20)可知，对于固体物质 Si→−∞．因此，为了近似描述固体加入流道后对流体流动的影响，在固体区域添加一个足够大的体积力以阻碍流体的流动．

本节中将的理想流场作为参考流场．首先设定动压头的阈值，即如果原始流场中某处动压 pd,ori与理想流场区域内该处的动压 pd,op之差大于该阈值，那么需要在该区域填充固体以减小动压．需要指出，pd阈值的选取视实际要求而定，譬如压降、混合效果等因素．

随着混合效果的提高，系统的压降也随之增加．在图5中，随着固体体积分数的提高压降不断提高，而IOS值呈现出先降低而后趋于稳定的趋势．这是因为加入固体阻碍流体流动，而不是促进流体流动，因此是一种被动方式的强化手段．而理想流场是通过向计算区域内添加虚拟体积力的方式实现的，因此以该方式得到的理想流场不能完全通过添加固体来实现，这也是造成IOS值趋于稳定的原因．图6为固体体积分数为6.10%时的速度分布以及氨气质量分数分布，由于固体结构的存在，流场及氨气质量分数分布都有了明显变化.

图5 压降和离析度随固体体积分数的变化Fig.5 Variationsof the pressure drop and the intensity of segregation with solid volume fraction

图6 固体体积分数为6.10%时流场内速度分布及氨气质量分数分布Fig.6 Contours of velocity magnitude and mass fraction of ammonia in the flow pattern with solid volume fraction of 6.10%

4 结 论

本文提出一种混合过程流场构造的理论化方法，通过调整不同传质机制下的熵产达到强化混合的目的．针对特定的气体混合过程，建立相应的数学模型，并推导出特定流型结构的控制方程组．通过添加虚拟体积力的方式改变流型结构，强化混合过程．基于优化流场，对混合器内部结构进行改造．主要结论如下．

(1) 以混合熵产为目标函数对混合过程进行优化，得到了优化流场的控制方程．控制方程中的虚拟体积力改变了流场结构，从而促进了氨气和空气的混合，经过优化后出口离析度降低了一个数量级，从0.153,84降低到0.012,67，同时压降有所提升．

(2) 计算结果表明参数 C3对优化流场的影响较大．随着 C3的增大，黏性耗散逐渐变大，出口处的离析度随之减小，混合均匀程度增加．

(3) 优化流场对混合器设计具有指导意义．本文基于优化流场并借助多孔介质模型，对混合设备进行优化设计．提出以动压头作为判断标准，向混合器内添加虚拟介质．分别设定不同的动压头阈值，得到不同固体体积分数下的流场．计算表明随着固体体积分数的提高，压降逐渐增大，而离析度逐渐降低而后趋于一定值．

［1］ Bejan A. A study of entropy generation in fundamental convective heat transfer[J]. ASME Journal of Heat Transfer，1979，101(4)：718-725.

［2］ Bejan A. Entropy Generation Through Heat and Fluid Flow[M]. New York：John Wiley & Sons，1982.

［3］ Bejan A. Second-law analysis in heat transfer and thermal design[J]. Advances in Heat Transfer，1982，15：1-58.

［4］ Bejan A. Second law analysis in heat transfer[J]. Energy，1980，5(8/9)：702-732.

［5］ Bejan A. Concept of irreversibility in heat exchanger design：Counterflow heat exchangers for gas-to-gas applications[J]. ASME Journal of Heat Transfer，1977，99(3)：374-380.

［6］ San J Y，Worek W M，Lavan Z. Entropy generation in combined heat and mass transfer[J]. International Journal of Heat and Mass Transfer，1987，30(7)：1359-1369.

［7］ Carrington C G，Sun Z F. Second law analysis of combined heat and mass transfer phenomena[J]. International Journal of Heat and Mass Transfer，1991，34(11)：2767-2773.

［8］ Yao S G. Analysis of entropy generation of combined heat and mass transfer in internal and external flows with the assumption of local thermodynamic equilibrium[J]. Journal of Thermal Science，1994，3(1)：1-6.

［9］ Bejan A. Shape and Structure，from Engineering to Nature[M]. Cambridge，UK：Cambridge University Press，2000.

［10］ Bejan A，Lorente S. Constructal theory of generation of configuration in nature and engineering[J]. Journal of Applied Physics，2006，100(4)：041301-1-041301-27.

［11］ Bejan A. Constructal-theory network of conducting paths for cooling a heat generating volume[J]. International Journal of Heat and Mass Transfer，1997，40(4)：799-816.

［12］ Tondeur D，Luo L A. Design and scaling laws of ramified fluid distributors by the constructal approach[J]. Chemical Engineering Science，2004，59(8/9)：1799-1813.

［13］ Azoumah Y，Neveu P，Mazet N. Optimal design of thermochemical reactors based on constructal approach[J]. AIChE Journal，2007，53(5)：1257-1266.

［14］ Tescari S，Mazet N，Neveu P. Constructal method tooptimize solar thermochemical reactor design[J]. Solar Energy，2010，84(9)：1555-1566.

［15］ Wu W J，Chen L G，Sun F R. On the “area to point”flow problem based on constructal theory[J]. Energy Conversion and Management，2007，48(1)：101-105.

［16］ Boichot R，Luo L A，Fan Y L. Tree-network structure generation for heat conduction by cellular automaton[J]. Energy Conversion and Management，2009，50(2)：376-386.

［17］ Boichot R，Luo L A. A simple cellular automaton algorithm to optimize heat transfer in complex configurations[J]. International Journal of Exergy，2010，7(1)：51-64.

［18］ Wang L M，Fan Y L，Luo L A. Heuristic optimality criterion algorithm for shape design of fluid flow[J]. Journal of Computational Physics，2010，229(20)：8031-8044.

［19］ Guo Z Y，Zhu H Y，Liang X G. Entransy—A physical quantity describing heat transfer ability[J]. International Journal of Heat and Mass Transfer，2007，50(13/14)：2545-2556.

［20］ Chen Q，Ren J X，Guo Z Y. Field synergy analysis and optimization of decontamination ventilation designs[J]. International Journal of Heat and Mass Transfer，2008，51(3/4)：873-881.

［21］ Chen Q，Meng J A. Field synergy analysis and optimization of the convective mass transfer in photocatalytic oxidation reactors[J]. International Journal of Heat and Mass Transfer，2008，51(11/12)：2863-2870.

［22］ Hirschfelder J O，Curtiss C F，Bird R B. Molecular Theory of Gases and Liquids[M]. New York：John Wiley & Sons，1954.

［23］ Meng J A，Liang X G，Li Z X. Field synergy optimization and enhanced heat transfer by multi-longitudinal vortexes flow in tube[J]. International Journal of Heat and Mass Transfer，2005，48(16)：3331-3337.

［24］ Schönfeld F，Hardt S. Simulation of helical flows in microchannels[J]. AIChE Journal，2004，50(4)：771-778.

［25］ Rosaguti N R，Fletcher D F，Haynes B S. Low-Reynolds number heat transfer enhancement in sinusoidal channels[J]. Chemical Engineering Science，2007，62(3)：694-702.

［26］ Jia H，Liu W，Liu Z C. Enhancing convective heat transfer based on the minimum power consumption principle[J]. Chemical Engineering Science，2012，69(1)： 225-230.

［27］ Massman W J. A review of the molecular diffusivities of H2O，CO2，CH4，CO，O3，SO2，NH3，N2O，and NO2in air，O2and N2near STP[J]. Atmospheric Environment，1998，32(6)：1111-1127.

［28］ Chen Q，Wang M，Pan N. Optimization principles for convective heat transfer[J]. Energy，2009，34(9)：1199-1206.

［29］ Danckwerts P V. The definition and measurement of some characteristics of mixtures[J]. Applied Scientific Research，1952，A3(4)：279-296.

(责任编辑：田 军)

An Approach to Mixing Equipment Optimization Based on Flow Pattern Construction

Liu Chunjiang1,2，Zhao Ming'en1,2，Guo Kai1,2，Qi Wenzhe1,2，Huang Zheqing1,2，Liu Botan1,2
(1. School of Chemical Engineering and Technology，Tianjin University，Tianjin 300072，China；2. State Key Laboratory of Chemical Engineering(Tianjin University)，Tianjin 300072，China)

In the present study，an approach tomixing equipment optimization based on flow pattern construction was proposed. Namely，the specific flow pattern was constructed to enhance the mixing process. To obtain the desired flow pattern，a Lagrange multiplier equation，with the entropy generation as the objective function and some global constraints，was constructed. The solution of the Lagrange equation represented the flow pattern extremizing the entropy generation subject to a given viscous dissipation rate. The simulation results revealed that the flow pattern constructed by extremizing the entropy generation contributed to an improvement in mixing performance. In order to demonstrate the applicability of this approach，the mixing for a mixture of ammonia/air involved in the flue gas denitration process was studied by constructing the specific flow pattern in which the mixing performance was improved. Finally，according to the specific flow pattern，a mixer with internal structure was designed by employing the porous media model.

mixing process enhancement；flow pattern construction；calculus of variations；equipment optimization design

TQ027.1

A

0493-2137(2015)03-0255-07

10.11784/tdxbz201401006

2014-01-03；

2014-03-26.

国家重点基础研究发展计划(973计划)资助项目(2012CB720500)；国家自然科学基金资助项目(21176171，21406157)；天津市自然科学基金重点资助项目(12JCZDJC28700)．

刘春江（1970— ），男，博士，教授.

刘春江，cjliu@tju.edu.cn.

时间：2014-04-01.

http://www.cnki.net/kcms/doi/10.11784/tdxbz201401006.html.