等应力比加载路径下堆石料力学特性的细观数值分析

马 刚，井向阳，胡 超，常晓林，周 伟

(1. 武汉大学水资源与水电工程科学国家重点实验室，武汉 430072；2. 中国电建集团成都勘测设计研究院有限公司，成都 610072)

等应力比加载路径下堆石料力学特性的细观数值分析

马 刚1，井向阳2，胡 超1，常晓林1，周 伟1

(1. 武汉大学水资源与水电工程科学国家重点实验室，武汉 430072；2. 中国电建集团成都勘测设计研究院有限公司，成都 610072)

堆石料的力学特性与应力路径相关，而常规三轴试验的应力路径与堆石坝工程填筑期坝体内的应力路径差别较大，因此本文采用考虑颗粒破碎效应的随机颗粒不连续变形分析(SGDD)方法进行等应力比加载路径下堆石料三轴试验的细观数值模拟，研究固结应力和加载应力比对堆石料强度和变形特性的影响．模拟结果表明：固结应力和加载应力比对堆石料的力学特性影响较大，随着固结应力的增加、加载应力比的减小，应力应变曲线由应变软化型向硬化型转化，试样也由低压剪胀向高压剪缩转变；p-q平面内的强度包络线具有明显的非线性；细观组构量的演化规律与堆石料的宏观力学特性密切相关．

堆石料；应力路径；等应力比；细观数值模拟；非线性强度；细观组构

堆石料的力学特性具有非线性、压硬性、剪胀性、各向异性，还具有应力路径相关性．300,m级高堆石坝工程的建设需求，对堆石料力学特性的研究提出了更高的要求．受试验条件的限制，对堆石料力学特性的研究大多采用围压不变的常规三轴试验，而大量的工程实测结果表明，堆石坝工程在填筑期的应力路径近似为等应力比路径，蓄水期应力路径发生偏转，呈复杂的应力路径形态[1]．因此复杂应力路径下堆石料的力学特性研究已成为目前的研究热点之一．堆石料复杂应力路径的大型三轴试验研究虽然开展得较晚，但近些年已取得了一些研究成果[2-10]．

由于复杂应力路径下的大型三轴试验较常规三轴试验更为复杂，同时为了获得不同应力路径下的强度和变形参数，需要进行多个围压下的三轴试验．因此，开展数个不同级配堆石料应力路径大型三轴试验将耗费大量人力、物力和财力，且难以实时观测堆石料的细观组构．而细观数值模拟可以动态地观察细观组构的演化过程，包括观察颗粒的运动、进行细观组构的量化、提取组构量的演化规律，还可以方便快捷地进行大量的敏感性分析．通过将数值模拟与试验结合起来，相互印证、补充，可以揭示一些复杂的机理，丰富人们对堆石料这种复杂材料的认识．

为了模拟可变形和破碎的颗粒集合体的动力学问题，Munjiza[11]提出了连续-离散耦合分析方法，该方法融合了有限单元法和离散单元法的优势和长处，大大扩展了有限单元法和离散单元法的应用范围.周伟等[12-15]基于连续-离散耦合分析方法，发展了随机颗粒不连续变形(stochastic granular discontinuous deformation，SGDD)方法．SGDD采用 Munjiza-NBS算法检索颗粒间的接触状态，基于罚函数法的接触力模型计算颗粒间的接触力，采用二阶四面体单元离散颗粒以提高计算精度、改善应力自锁现象，基于显式时步步进的方法进行节点动力平衡方程的时域积分．考虑实际堆石料一般由棱角状和亚棱角状的颗粒组成，提出了不规则多面体颗粒的随机生成算法，通过改变颗粒外包椭球的长短轴比和颗粒表面的顶点数来控制颗粒的形态和圆度，使其更接近真实的堆石颗粒[14]．

本文采用考虑颗粒破碎的 SGDD方法，进行堆石料等应力比加载路径三轴试验的细观数值模拟，研究固结应力和加载应力比对堆石料强度和变形特性的影响，分别从宏观和细观两个尺度分析了数值模拟结果，深入分析了不同应力路径条件下堆石料的抗剪强度、应力应变、体积应变等复杂剪切特性，揭示其细观组构与宏观力学特性，特别是与应力路径相关性的内在联系．

1 基于岩石劣化模型的颗粒破碎模拟

颗粒破碎对堆石料的强度和变形特性有显著影响，在堆石料的细观数值模拟中合理地体现颗粒破碎效应至关重要．在基于变形体离散元的 SGDD方法中引入黏聚力模型(CZM)和界面单元使其具有模拟开裂的能力[15]．这种模拟颗粒破碎的方式比较直观，能反映颗粒破碎对堆石料力学特性的主要影响，模拟结果符合试验规律．由于颗粒破碎位置的不确定性，在颗粒内部的所有细观单元之间都要插入界面单元，导致计算成本急剧上升，以一个含有7,124个颗粒的堆石料试样为例，采用二阶四面体网格离散为156,161个实体单元，需要插入326,620个界面单元[15]．

采用损伤劣化模型模拟破碎放弃了对颗粒破碎形式显式直观的表达，侧重于考虑颗粒破碎对堆石料力学特性的影响．本文采用一种通用岩石劣化模型[16](rock deterioration model，RDM)来模拟颗粒的破碎效应．该模型的应力应变关系具有明显的线弹性段、软化段和塑性流动段，是一个典型的弹-脆-塑性模型．图1是采用RDM模拟的一个岩石三轴压缩试验，在 RDM中，岩体力学参数随等效塑性应变发生变化，在模型的弹性阶段，其应力应变曲线是线性的；进入屈服阶段后，模型参数即发生了劣化，应力应变曲线表现出明显的应力跌落过程；当塑性应变达到临界塑性应变后，模型参数劣化到稳定值，应力应变曲线表现为塑性流动．

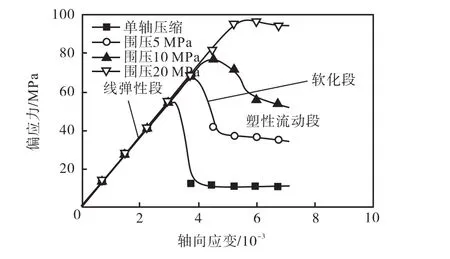
图1 RDM典型的应力应变关系曲线Fig.1 Typical stress-strain relationship curves of RDM

2 数值试样与试验方案

2.1 数值试样

采用随机模拟技术生成三维凸多面体颗粒，再压缩成指定大小的数值试样[14]．数值试样尺寸为 φ,300 mm×615,mm，最大粒径maxd =60,mm，孔隙率为30%，共生成 8,586个颗粒，采用二阶四面体网格离散为111,572个实体单元，323,884个节点．图2为数值试样及其颗粒级配曲线．

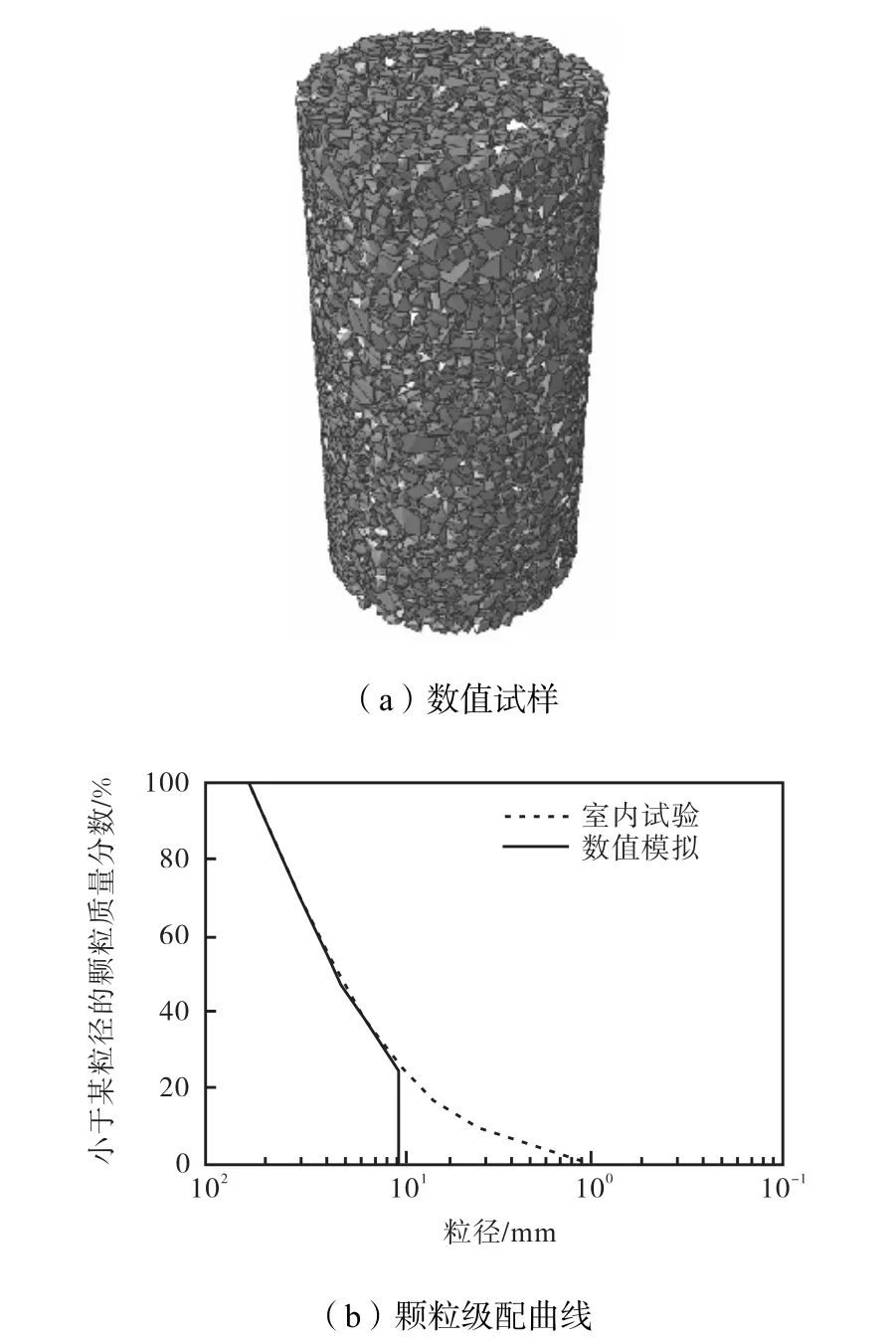
图2 数值试样及其颗粒级配曲线Fig.2 Numerical specimen and particle size distributioncurve

细观参数取值是数值试验的关键，在考虑破碎的堆石体随机颗粒不连续变形方法中，有两类参数．一是颗粒间接触特性参数，如 Kn、Ks和摩擦系数u．由于缺乏成熟的试验设备和测试技术，关于这些参数的试验成果鲜见发表，文献[17-18]收集和整理了关于颗粒间摩擦系数的试验成果，一般可以认为堆石颗粒间的摩擦系数在0.35～0.70之间，且随着颗粒粒径的增大，摩擦系数有减小的趋势，但这个规律在很大的粒径跨度范围内才能体现出来，而本文数值试验的颗粒粒径在10～60,mm之间，其粒径的跨度相对较小，可以认为摩擦系数为同一值．另一类参数是反映颗粒变形和强度的参数，如弹性模量E、单轴抗压强度 fc等. 由于参数较多，且大部分不能通过试验直接获取，只能采用类比或试算的方法间接确定．本文通过调整细观参数，使数值模拟得到的应变应力曲线和接近室内三轴试验成果，如图3所示．表1为最终的细观参数．室内试验成果来自长江科学院所做的双江口堆石料三轴试验．2.2 试验方案

为了研究堆石料在不同应力路径下的力学特性，分别进行了常规三轴试验、等应力比记载试验的细观数值模拟．p-q平面内的加载应力比路径见图 4，各参数的定义见表2．

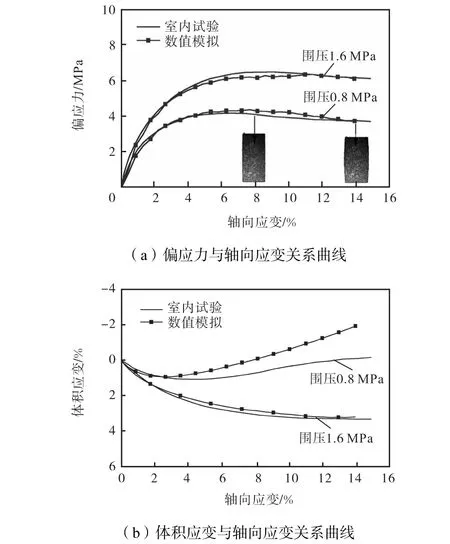
图3 数值模拟结果与试验结果的比较Fig.3 Comparison of numerical simulation results and test results

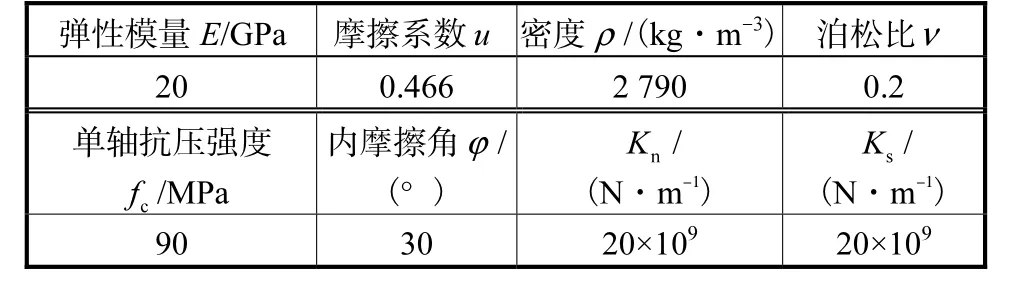
表1 细观参数Tab.1 Mechanical parameters

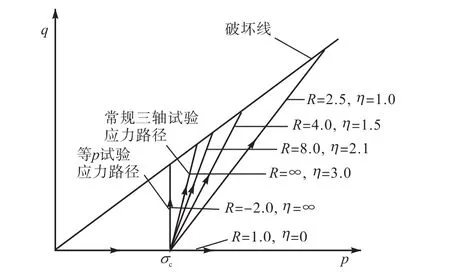
图4 p-q平面内的加载应力路径Fig.4 Loading stress paths in p-q plane

常规三轴试验选取4个固结应力 σc，分别为0.4,MPa、0.8,MPa、1.2,MPa、1.6,MPa．在常规三轴试验中，σ3保持不变，即 dσ3为 0，对应于

等应力比加载试验选取 4个主应力比R，分别为 1.5、2.5、4.0、8.0，对应的应力比η分别为 0.43、1.0、1.5、2.1．

表2 参数定义Tab.2 Definition of parameters

数值模拟时，先对试样施加固结应力 σc，固结完成后再剪切，剪切速率为 0.000,1,mm/步．大主应力方向采用位移控制加载，提取上一时步大主应力方向的反作用力计算得到 σ1，再根据主应力比计算出 σ3，将其施加到试样上．

3 宏观力学响应分析

3.1 应力应变关系

不同固结应力 σc下，各个加载应力路径的偏应力与剪应变、平均主应力与体积应变、偏应力与轴向应变的关系曲线分别如图5～图7所示，受篇幅限制只列出固结应力为 0.4,MPa和 1.2,MPa的模拟结果．分析试验结果，可以得到应力路径下堆石料应力应变的规律如下．

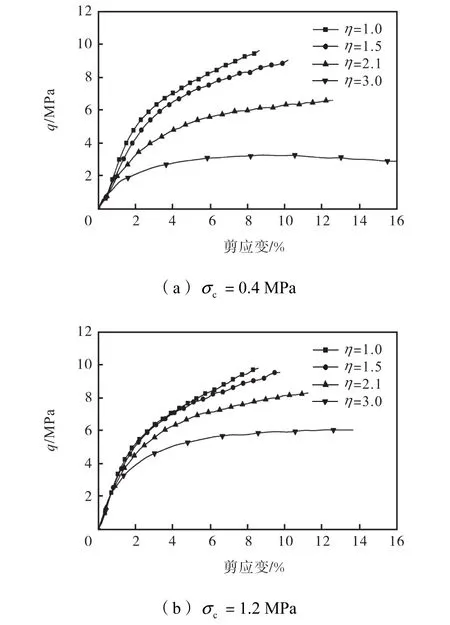
图5 不同固结应力下偏应力与剪应变关系曲线Fig.5 Relationship curves of deviational stress and shear strain under different consolidation stresses

(1) 峰值偏应力随固结应力的增大而增大；试样在低固结应力、高加载应力比(如时应力应变曲线表现为弱应变软化型，达到强度峰值后强度有所降低，但软化的程度较小，说明粗粒料的应变软化没有细粒土那么显著，其在峰值后仍可承受较大应力作用；随着固结应力的增加、加载应力比的减小，应力应变曲线由应变软化型向硬化型转化；高固结应力、低加载应力比(如应力应变曲线几乎都是应变硬化型．

(2) 当加载应力比较大时，如常规三轴试验应力路径，体积应变由低压剪胀向高压剪缩发展；当加载应力比较小时，试样始终为剪缩变形．

(3) 如图7所示，固结应力 σc一定时，对于相同的轴向应变，试样的偏应力随加载应力比的增加而逐渐减小；固结应力较小时，加载应力比对应力应变曲线的影响较大，对于相同的轴向应变，不同加载应力比对应的偏应力差别显著；而固结应力较大时，加载应力比的影响就比较小；加载应力比对试样应力应变曲线的影响也随应力比的减小而逐渐衰弱．3.2 抗剪强度特性

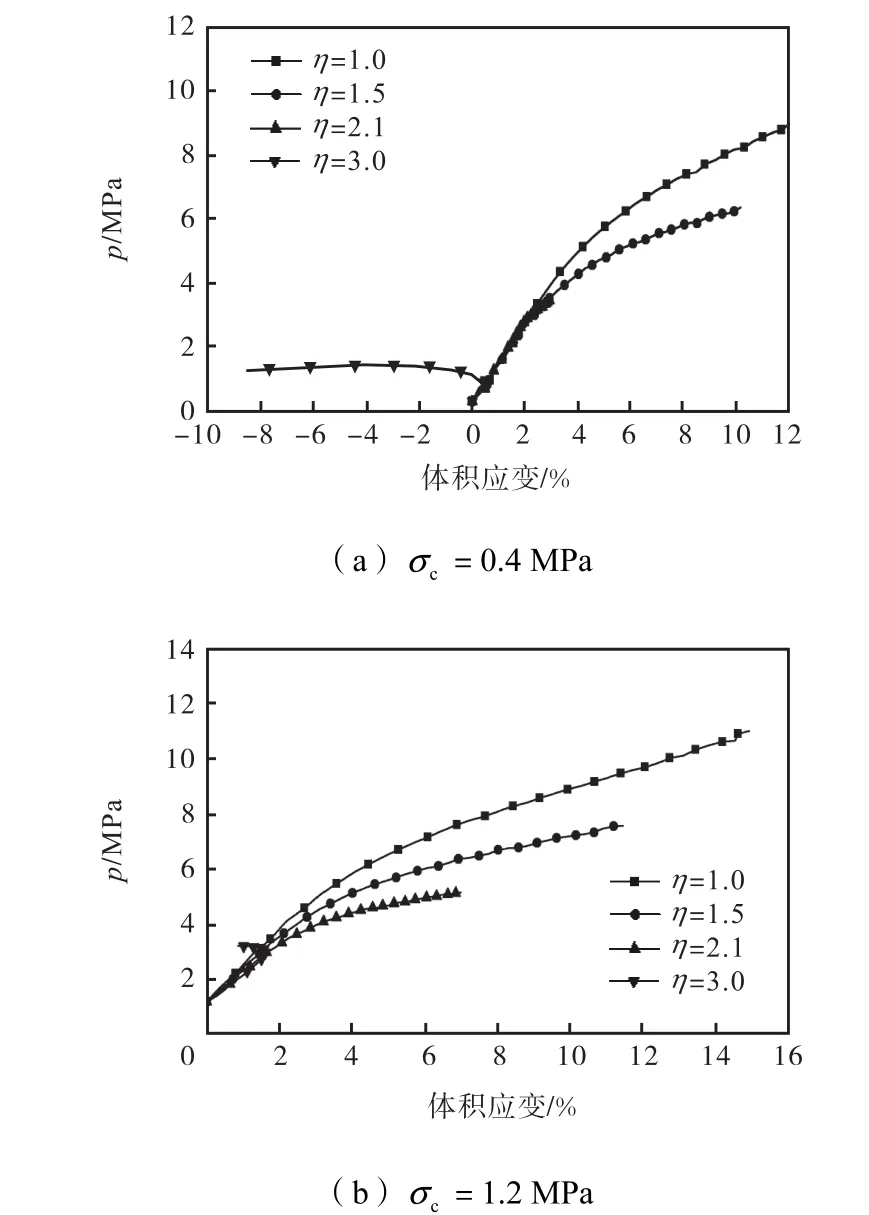
图6 不同固结应力下平均应力与体积应变关系曲线Fig.6 Relationship curves of mean stress and volumetric strain under different consolidation stresses

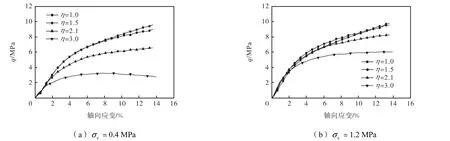
图7 不同固结应力下偏应力与轴向应变关系曲线Fig.7 Relationship curves of deviational stress and axial strain under different consolidation stresses

由不同应力路径下试样破坏时的应力状态计算破坏时的内摩擦角 ϕf和应力比 Mf分别为

式中 σ1,f和 σ3,f分别为试样的峰值大主应力和小主应力．计算结果见表3．

将不同应力路径下试样破坏时的应力状态绘于p-q平面，见图 8．从图 8可以看出，堆石料具有剪切和压缩两种破坏形式，在高平均应力下，破坏类型不再是剪切破坏，而是剪切和压缩共同作用导致的破坏．这是由于随着应力比的减小，试样逐渐呈各向等压应力状态，此时堆石颗粒在高应力作用下破碎明显，小颗粒填充试样的孔隙，在应力应变曲线上表现出较强的剪缩和应变硬化特征．在本文的数值模拟中，当 p< 9.5MPa时，强度包络线为剪切破坏面，而p≥ 9.5MPa为压缩破坏面．

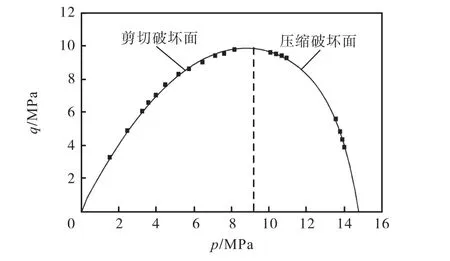
图8 p-q平面上的强度包络线Fig.8 Strength envelope in p-q plane

堆石料的剪切强度包络线具有明显的非线性，随着平均应力的增加强度包络线明显下弯，低围压下堆石料表现出较强的剪胀性，强度较高；随着平均应力的增加，颗粒接触应力超过其破碎强度，颗粒破碎效应逐渐占主导作用，而剪胀效应逐渐衰弱并消失，剪切强度逐渐降低．因此，在应力变化范围较大的情况下，采用非线性强度表达式描述抗剪强度更为合理.不同应力路径下试样破坏时的应力状态均落在图 8所示的强度包络线附近，说明应力路径对强度表达式的参数影响不大，这与刘萌成等[4]进行的应力路径下堆石料剪切特性试验研究的结论相同．

堆石料破坏时的内摩擦角 ϕf与围压 σ3的非线性关系可表示为

式中：ϕ0、Δϕ 为模型参数，Δϕ 反映了非线性程度；pa为一个标准大气压．

如图9所示，在不同应力比η下的加载应力路径试验中，内摩擦角 ϕf与固结应力 σc(常规三轴应力路径中的关系均可以用式(4)描述．值得注意的是，内摩擦角不仅与固结应力 σc有关，还与加载应力比有关，固结应力 σc相同时，应力比η越小，内摩擦角 ϕf越小．以 σc= 0.8MPa 为例，η = 1.0时 ϕf= 23.57，而 η= 3.0(常规三轴剪切试验所对应的应力比)时 ϕf= 49.02，两者相差超过 1倍．这一现象同样可以用颗粒破碎来解释，应力比η越小，在加载过程中施加在试样上的围压 σ3越大，限制了试样侧向的变形，导致颗粒间的约束作用增强，使颗粒之间不易发生翻越、错动等相对运动，增大了轴向的承载能力．然而颗粒间的约束作用越强，其接触力也越大，超过堆石料母岩强度时，颗粒发生破碎，弱化了堆石料的剪胀效应，导致抗剪强度参数降低．由图9(a)可以看出，试样破坏时的内摩擦角 ϕf和相应的平均应力p落在同一条曲线附近，它们的关系可以用一个表达式描述，这里采用与式(4)相似的表达式，不同的是式(4)中的围压 σ3替换为破坏时的平均应力p，即，拟合得到14.46，相关系数为0.9918．

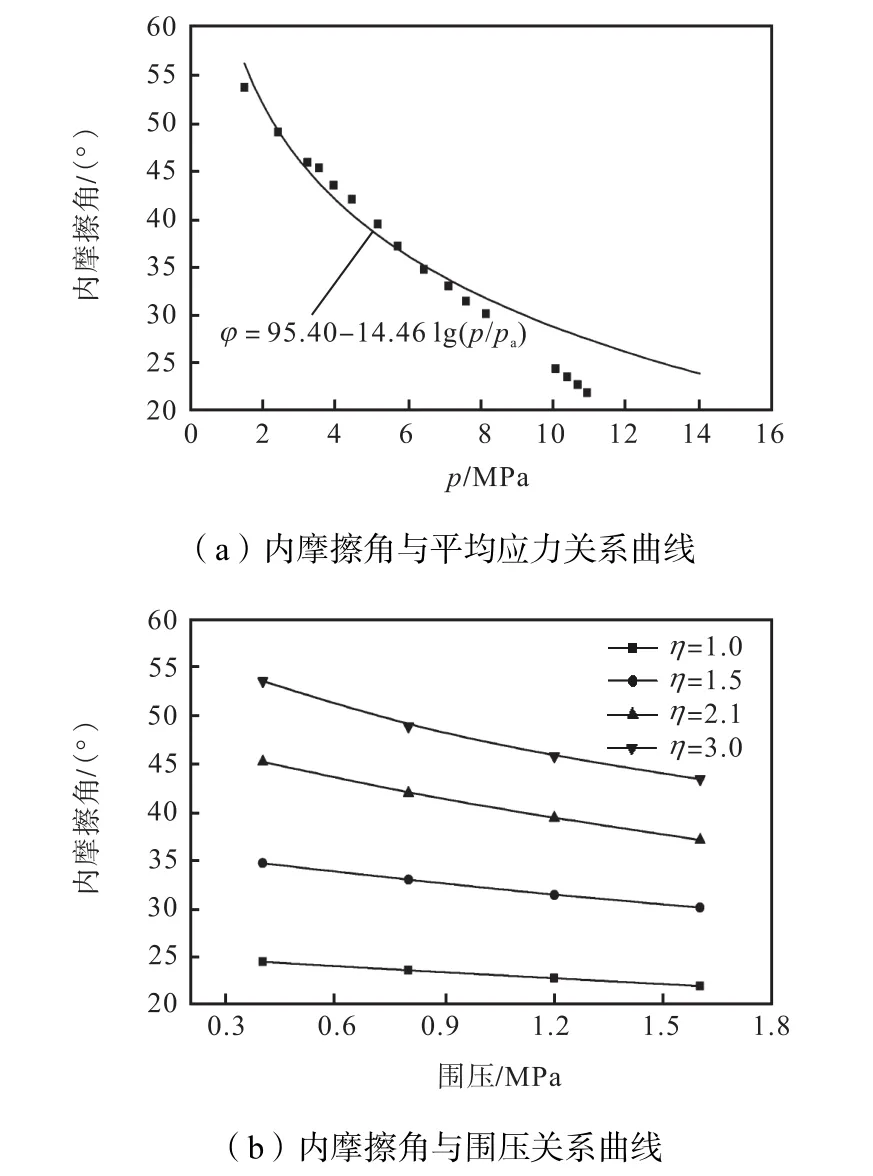
图9 内摩擦角与平均应力和围压的关系曲线Fig.9 Relationship curves of internal friction angel and mean stress，hydrostatic pressure

将不同固结应力 σc、应力比η下试样的破坏应力比 Mf′与平均应力p绘于图10，其规律与图9所示的内摩擦角 ϕf与平均应力p的关系相似，采用如下表达式可以较好地描述发生剪切破坏时试样的破坏应力比

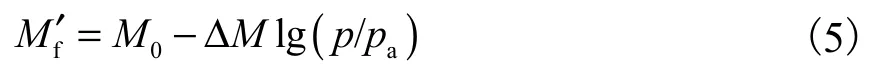
式中：Mf′为破坏应力比；M0、ΔM 为模型参数．

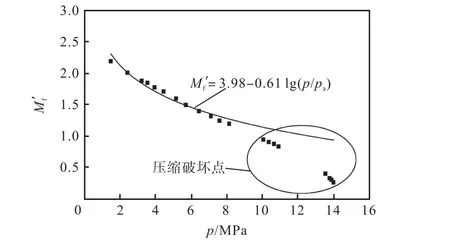
图10 破坏应力比与平均应力的关系曲线Fig.10 Relationship curves of failure stress ratio and mean stress

联立式(2)和(5)可以得到 p-q面上剪切破坏线的表达式

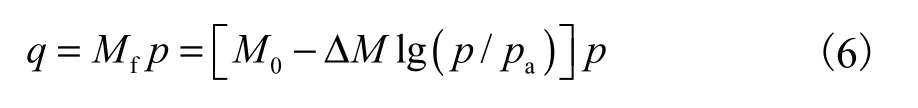
p-q平面上剪切破坏线的各种表达式拟合曲线见图11．采用线性强度表达式的拟合精度较差；幂函数表达式(B为拟合参数)的拟合精度也不高；式(6)拟合出的剪切破坏线与破坏点比较吻合，但是其不满足 p→ 0时 q→ 0的条件，故不适用于描述堆石料剪切强度；双曲线型表达式拟合出的剪切破坏线与试验点较吻合，而且表达式无奇异性，是描述堆石体抗剪强度的理想选择之一．

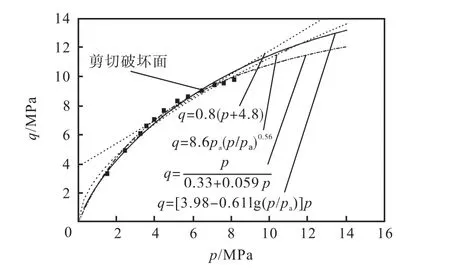
图11 p-q平面上剪切破坏线的拟合曲线Fig.11 Fitting curves of shear strength line in p-q plane

压缩破坏线是封闭的，一端与 p轴相接，另一端与剪切破坏面相接，其形状通常是椭圆形，其表达式为

从图 12可以看出，采用双曲线型的剪切破坏线和椭圆形的压缩破坏线与数值试验结果比较吻合．

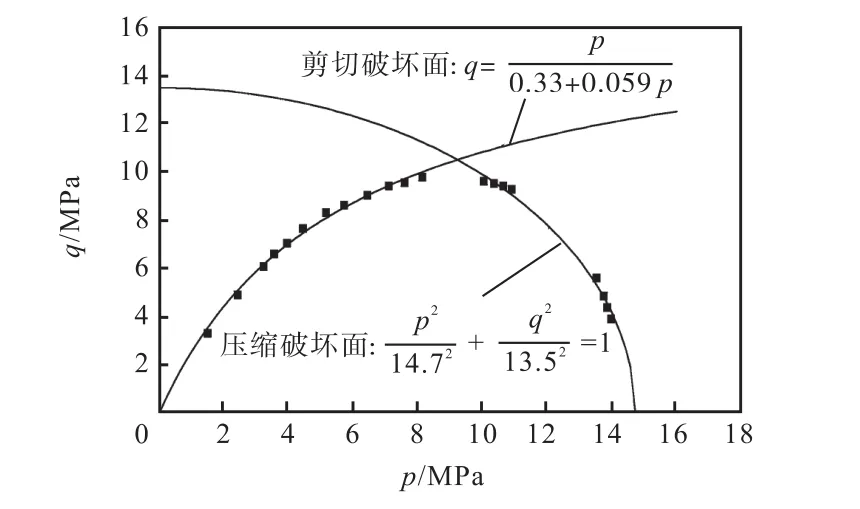
图12 p-q平面上强度包络线的双破坏面拟合曲线Fig.12 Fitting curves of double yield surface in p-qplane

4 细观组构演化分析

堆石料的颗粒组成、颗粒排列方式和粒间接触力是决定其宏观力学特性的重要因素，而数值模拟最明显的优势在于可以实时地观察颗粒在加载过程中的运动规律，提取试样的细观组构参数，如颗粒配位数、长轴的定向、组构各向异性演化等．

图 13为固结应力一定时，不同加载应力路径下试样的颗粒配位数在剪切过程中的演化过程．低应力比加载路径下试样的颗粒配位数大于高应力比加载路径，这是由于试样在低应力比加载路径下颗粒破碎明显，破碎产生的小颗粒与其周围颗粒产生新的接触关系，试样更加密实，产生明显的剪缩特性．而在高应力比加载路径试验中，由于施加在试样上的围压相对较小，颗粒间的约束作用较弱，颗粒在剪切过程中容易发生翻转，导致颗粒之间的有效接触数减少，试样的孔隙率增大，试样的细观结构更加松散，这种现象在剪切带附近更为明显．

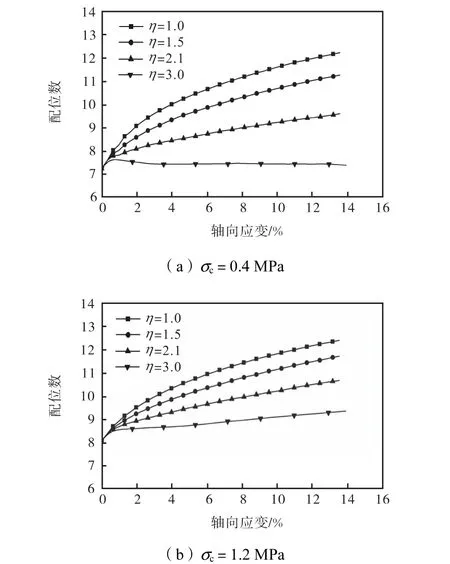
图13 不同加载应力路径下的颗粒配位数演化过程Fig.13 Evolution of coordination number under different loading stress paths

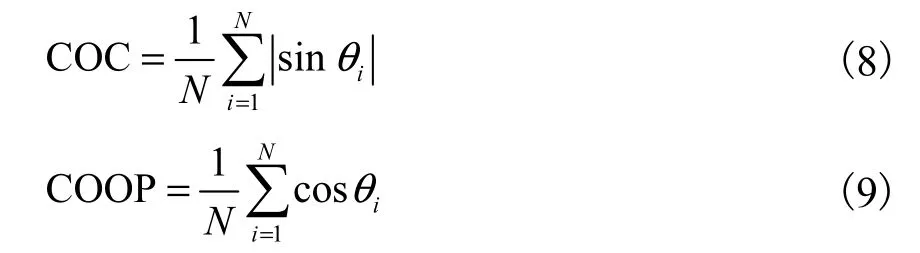
为了研究颗粒接触法向的演化规律与颗粒形状的关系，定义颗粒的接触法向系数(contact orientation coefficient，COC)和颗粒的接触法向向列数(contact orientation order parameter，COOP)为

式中：N为颗粒接触数；θi为颗粒接触法向与水平向的夹角；COC反映了颗粒接触法向的主方向，COC接近于 1，表明颗粒接触法向以竖直向居多，COC接近于 0，表明颗粒接触法向以水平向居多；COOP反映了颗粒接触法向的各向异性，COOP越小，各向异性越明显．

图 14为固结应力一定时，不同加载应力路径下试样的接触法向系数COC在加载过程中的演化过程．在加载过程中，接触法向系数COC逐渐增大，表明颗粒接触的法线方向逐渐向加载方向倾斜；在高应力比加载路径中，由于试样周边的约束作用相对较小，接触方向向轴向加载方向演化的趋势更为明显；而在低应力比加载路径中，试样的应力状态趋近于各向等压，轴向和侧向施加在试样上的作用差别较小，没有一个明显的主方向．

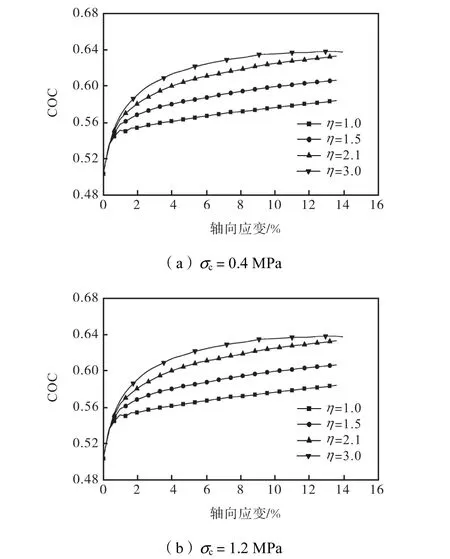
图14 不同加载应力路径下的COC演化过程Fig.14 Evolution of COC under different loading stress paths

图 15为固结应力一定时，不同加载应力路径下COOP在加载过程中的演化过程．在加载过程中，COOP逐渐减小，表明颗粒间接触的各向异性程度逐渐增强，试样表现出明显的应力诱导各向异性；应力比η越大，施加在试样上的各向应力差别越大，由此产生的各向异性程度越明显．

综合以上分析，堆石料的宏观力学特性与加载过程中细观组构的演化规律密切相关．在低固结应力、高应力比加载路径下，作用在试样上的侧向约束较小，轴向和侧向应力差别较大，导致颗粒容易产生相对运动，细观组构的各个要素发生演化，具体来说颗粒的配位数先增加后减小，颗粒间接触方向逐渐向轴向旋转，颗粒间接触的各向异性程度增强，在宏观上试样的应力应变曲线表现出明显的软化和剪胀特性；而在高固结应力、低应力比加载路径下，作用在试样上的侧向约束增强，颗粒接触紧密，限制了颗粒间的相对运动，同时颗粒破碎明显，在细观组构的演化上，颗粒配位数逐渐增加，颗粒间的接触方向向轴向加载方向旋转的趋势不太明显，由于应力诱导的各向异性程度较低，在宏观上试样的应力应变曲线呈现出应变硬化和剪缩特性．

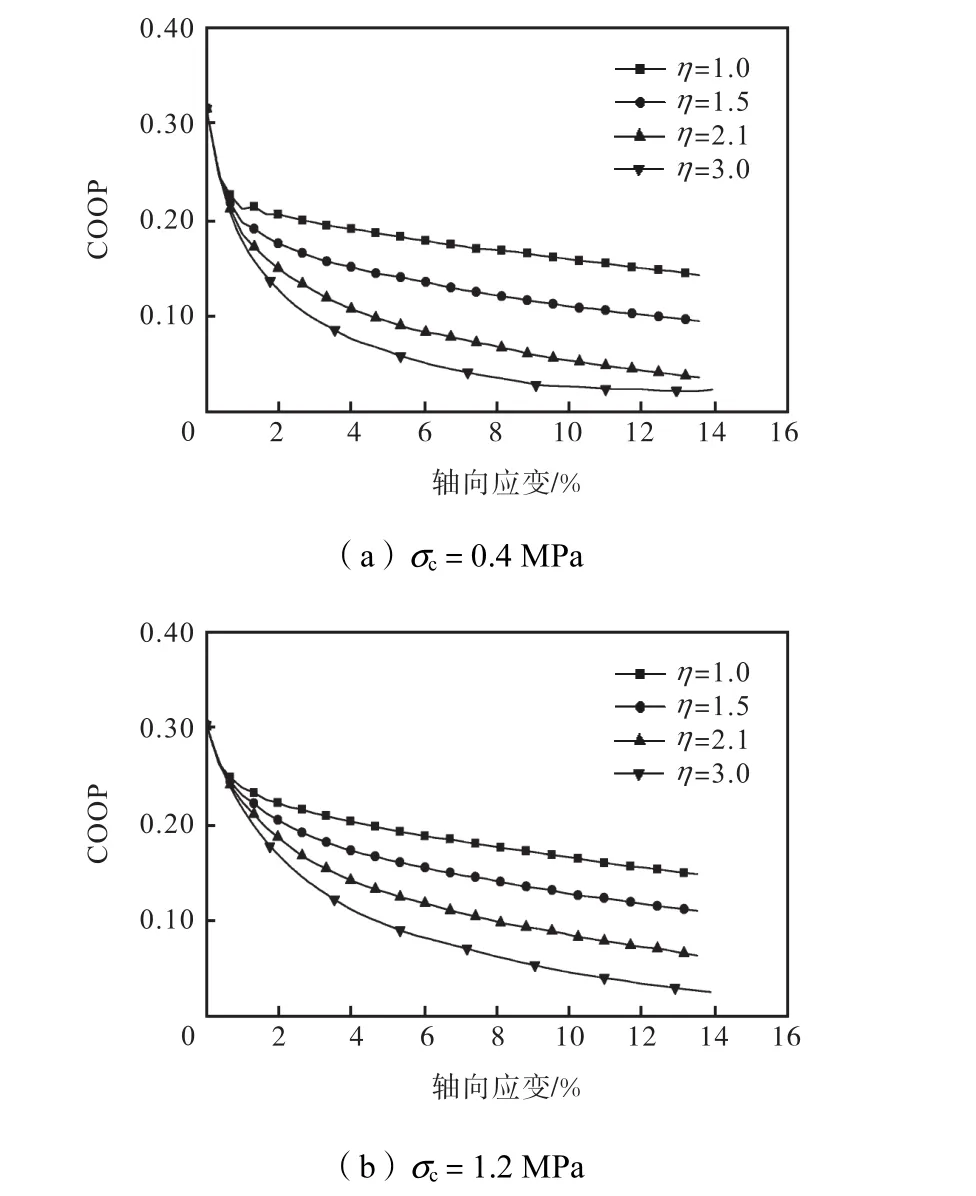
图15 不同加载应力路径下的COOP演化过程Fig.15 Evolution of COOP under different loading stress paths

5 结 论

本文采用考虑颗粒破碎效应的 SGDD方法对堆石料进行等应力比加载路径的细观数值模拟，研究固结应力和加载应力比对堆石料力学特性的影响，得出了以下结论．

(1) 试样在低固结应力、高加载应力比时应力应变曲线表现为弱应变软化型，达到强度峰值后强度有所降低，但降低幅度不大；随着固结应力的增加、加载应力比的减小，应力应变曲线由应变软化型向硬化型转化；高固结应力、低加载应力比应力应变曲线几乎都是应变硬化型．

(2) 当加载应力比较大时，如常规三轴试验应力路径，体积应变由低压剪胀向高压剪缩发展；当加载应力比较小时，试样始终为剪缩变形．

(3) 堆石料颗粒在高应力下破碎明显，使得强度包络线明显下弯，呈强非线性．因此，在应力变化范围较大的情况下，采用非线性强度模型描述抗剪强度更为合理．在高平均应力下，堆石料的破坏不再是剪切破坏，而是剪切和压缩共同作用导致的破坏．

(4) 堆石料的宏观力学特性与加载过程中细观组构的演化规律密切相关，细观组构量的演化规律与宏观的应力应变曲线的变化相对应．

［1］ 柏树田，周晓光，晁华怡. 应力路径对堆石变形特性的影响[J]. 水力发电学报，1999(4)：76-80.

Bai Shutian，Zhou Xiaoguang，Chao Huayi. Effects of stress path on the deformation of rockfill materials[J]. Journal of Hydroelectric Engineering，1999(4)：76-80 (in Chinese).

［2］ 柏树田，周晓光. 堆石在平面应变条件下的强度和应力-应变关系[J]. 岩土工程学报，1991，13(4)：33-40.

Bai Shutian，Zhou Xiaoguang. Strength and stress strain relationship of rockfill under plane strain condition[J]. Chinese Journal of Geotechnical Engineering，1991，13(4)：33-40(in Chinese).

［3］ 陈生水，沈珠江，郦能惠. 复杂应力路径下无粘性土的弹塑性数值模拟[J]. 岩土工程学报，1995，17(2)：20-28.

Chen Shengshui，Shen Zhujiang，Li Nenghui. An elastoplastic model for cohesionless soils under complex stress paths[J]. Chinese Journal of Geotechnical Engineering，1995，17(2)：20-28(in Chinese).

［4］ 刘萌成，高玉峰，刘汉龙. 应力路径条件下堆石料剪切特性大型三轴试验研究[J]. 岩石力学与工程学报，2008，27(1)：176-186.

Liu Mengcheng，Gao Yufeng，Liu Hanlong. Study on shear behaviors of rockfill in large-scale triaxial tests under different stress paths[J]. Chinese Journal of Rock Mechanics and Engineering，2008，27(1)：176-186 (in Chinese).

［5］ 古兴伟，沈 蓉，张永全. 复杂应力路径下糯扎渡堆石料应力-应变特征研究[J]. 岩石力学与工程学报，2008，27(增1)：3251-3260.

Gu Xingwei，Shen Rong，Zhang Yongquan. Study on stress-strain properties of rockfill materials under different stress paths in Nozhadu project[J]. Chinese Journal of Rock Mechanics and Engineering，2008，27(Suppl 1)：3251-3260(in Chinese).

［6］ 张宗亮，贾延安，张丙印. 复杂应力路径下堆石体本构模型比较验证[J]. 岩土力学，2008，29(5)：1147-1151.

Zhang Zongliang，Jia Yan′an，Zhang Bingyin. Comparison and verification of constitutive models for rockfill materials under complex stress path[J]. Rock and Soil Mechanics，2008，29(5)：1147-1151(in Chinese).

［7］ 相 彪，张宗亮，迟世春. 堆石料等应力比路径三模量增量非线性模型[J]. 岩土工程学报，2008，30 (9)：1322-1326.

Xiang Biao，Zhang Zongliang，Chi Shichun. Threemodulus incremental nonlinear model of rockfill under paths of constant stress ratio[J]. Chinese Journal of Geotechnical Engineering，2008，30(9)：1322-1326(in Chinese).

［8］ 杨 光，孙 逊，于玉贞，等. 不同应力路径下粗粒土力学特性试验研究[J]. 岩土力学，2010，31(4)：1118-1121.

Yang Guang，Sun Xun，Yu Yuzhen，et al. The testing research of mechanical properties of coarse-grained soil in different stress paths[J]. Rock and Soil Mechanics，2010，31(4)：1118-1121(in Chinese).

［9］ 相 彪，张宗亮，迟世春，等. 复杂应力路径下堆石料本构关系研究[J]. 岩土力学，2010，31(6)：1716-1722.

Xiang Biao，Zhang Zongliang，Chi Shichun，et al. Study of constitutive relations of rockfill under complex stress path[J]. Rock and Soil Mechanics，2010，31(6)：1716-1722(in Chinese).

［10］ 朱俊高，王元龙，贾 华，等. 粗粒土回弹特性试验研究[J]. 岩土工程学报，2011，33(6)：950-954.

Zhu Jungao，Wang Yuanlong，Jia Hua，et al. Experimental study on resilience behaviour of coarse grained soils[J]. Chinese Journal of Geotechnical Engineering，2011，33(6)：950-954(in Chinese).

［11］ Munjiza A. The Combined Finite-Discrete Element Method[M]. New York：John Wiley and Sons，2004：20-25.

［12］ 周 伟，常晓林，周创兵，等. 堆石体应力变形细观模拟的随机散粒体不连续变形模型及其应用[J]. 岩石力学与工程学报，2009，28(3)：491-499.

Zhou Wei，Chang Xiaolin，Zhou Chuangbing，et al. Stochastic granule discontinuous deformation model of rockfill and its application[J]. Chinese Journal of Rock Mechanics and Engineering，2009，28(3)：491-499(in Chinese).

［13］ 马 刚，周 伟，常晓林，等. 锚杆加固散粒体的作用机制研究[J]. 岩石力学与工程学报，2010，29(8)：1577-1584.

Ma Gang，Zhou Wei，Chang Xiaolin，et al. Study of anchorage mechanism of granular mixture[J]. Chinese Journal of Rock Mechanics and Engineering，2010，29(8)：1577-1584(in Chinese).

［14］ 马 刚，周 伟，常晓林，等. 堆石体三轴剪切试验的三维细观数值模拟[J]. 岩土工程学报，2011，33(5)：746-753.

Ma Gang，Zhou Wei，Chang Xiaolin，et al. 3D mesoscopic numerical simulation of triaxial shear tests for rockfill[J]. Chinese Journal of Geotechnical Engineering，2011，33(5)：746-753(in Chinese).

［15］ 马 刚，周 伟，常晓林，等. 考虑颗粒破碎的堆石体三维随机多面体细观数值模拟[J]. 岩石力学与工程学报，2011，30(8)：1671-1682.

Ma Gang，Zhou Wei，Chang Xiaolin，et al. Mesoscopic numerical simulation of rockfill considering particle breakage by using three-dimensional stochastic polyhedrons[J]. Chinese Journal of Rock Mechanics and Engineering，2011，30(8)：1671-1682(in Chinese).

［16］ 江 权，冯夏庭，陈国庆. 考虑高地应力下围岩劣化的硬岩本构模型研究[J]. 岩石力学与工程学报，2008，27(1)：144-152.

Jiang Quan，Feng Xiating，Chen Guoqing. Study on constitutive model of hard rock considering surrounding rock deterioration under high geostresses[J]. Chinese Journal of Rock Mechanics and Engineering，2008，27(1)：144-152(in Chinese).

［17］ 日本土质工学会. 粗粒料的现场压实[M]. 郭熙灵，文 丹，译. 北京：中国水利水电出版社，1998.

Japanese Society of Soil Mechanics and Foundation Engineering. Field Compaction of Coarse-Grained Materials[M]. Guo Xiling，Wen Dan，trans. Beijing：China Water Power Press，1998(in Chinese).

［18］ 李广信. 高等土力学[M]. 北京：清华大学出版社，2004.

Li Guangxin. Advanced Soil Mechanics[M]. Beijing：Tsinghua University Press，2004(in Chinese).

（责任编辑：樊素英）

Meso-Scale Numerical Analysis on Mechanical Properties of Rockfill Under Loading Path of Constant Stress Ratio

Ma Gang1，Jing Xiangyang2，Hu Chao1，Chang Xiaolin1，Zhou Wei1
(1. State Key Laboratory of Water Resources and Hydropower Engineering Science，Wuhan University，Wuhan 430072，China；2. PowerChina Chengdu Engineering Corporation Limited，Chengdu 610072，China)

The mechanical properties of rockfill are dependent on stress path, while the stress path in conventional triaxial test is different from that of rockfill during dam construction. Regarding this, the stochastic granular discontinuous deformation(SGDD)method is employed to study the rockfill at mesomechanical level. This study is aimed at exploring the relationship between the consolidation stress, loading stress ratio and macroscopic response of rockfill．Simulation results show that the consolidation stress and loading stress ratio exert a significant impact on the strength and deformation characteristics of rockfill. As the consolidation stress increases and loading stress ratio decreases，the type of stress strain relationship transfers from strain softening to hardening, meanwhile，the volumetric response transfers from dilation at low confining pressure to compaction at high confining pressure. The strength envelope in p-q plane shows obvious non-linear features. The evolution of mesoscopic fabric exhibits good uniformity with macroscopic response of rockfill.

rockfill；stress path；constant stress ratio；meso-scale numerical simulation；nonlinear strength；meso-scopic fabric

TV641

A

0493-2137(2015)03-0209-10

10.11784/tdxbz201308004

2013-08-01；

2014-04-05.

国家自然科学基金资助项目(51379161)；国家优秀青年科学基金资助项目(51322905).

马 刚（1985— ），男，博士，讲师，magang630@163.com.

周 伟，zw_mxx@163.com.