命题到底该怎样考查概念——以七年级上学期一些习题为例

☉江苏省如东县岔河中学 严冬梅

命题到底该怎样考查概念
——以七年级上学期一些习题为例

☉江苏省如东县岔河中学 严冬梅

命题研究一直是数学教学研究的重点之一，也是很多老师的兴趣点，加以各种各样名目繁多的考试，特别是中考、学期（年）期末统考的“现实引领”，各种命题“成果”在网络上传播得热闹非凡，客观地讲，绝大部分命题体现了数学老师的心血和智慧，但有些命题存在着一定的缺陷，特别是越往“底层”的学案单、周测、单元练的试题更是缺陷明显，有些试题的考查立意是关注概念，其实却是在歪曲、丑化数学概念，使得数学以一种怪怪的形象呈现在学生眼前，一定程度上让学生讨厌数学，影响着数学的形象.笔者列举一些“常见”的习题，商榷这些习题的命题立意，期待得到大家的批评指正.

一、考查概念的常见题及其商榷

例1式子-|π-3|等于（）.

A.π-3B.π+3C.3-πD.-3-π

商榷：这道题立意是考查有理数意义部分绝对值的化简，然而命题者为了增加所谓的解题层次，引入了无理数π进来，让学生辨析π-3的正负，再化简绝对值符号，然后前面再来一个“-”，使得习题的效度、信度下降，因为学生在任何一个环节出现阻碍，都难以成功解题.再说，除了个别版本的教材外，在有理数的意义部分，并没有引入无理数，一般都是在实数部分才引入这个概念，所以这里将π引入化简考查也是不恰当的，事实上，检索教材上的绝对值符号的化简，没有这样的习题.

例2单项式-3×102x2y的系数、次数分别为（）.

A.-3×102、二B.-3、五

C.-3、四D.-3×102、三

商榷：本意是考查单项式的系数、次数，出发点很好，但是命题者为了搞晕学生，综合了科学记数法进来，使得单项式“不伦不类”.如果认真思考单项式概念在全章的位置就会发现，单项式的概念是为多项式的概念服务的，只要学生能辨别数字因数、字母次数的和就行了，不必在此基础上再综合一些其他的知识点，搞晕学生，把数学引入繁杂、难理解的境地.

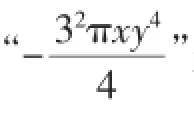
例4下列说法：①a为任意有理数，a2+1总是正数；②方程x+2＝是一元一次方程；③若ab＞0，a+b＜0，则a＜ 0，b＜0；④代数式都是整式；⑤若a2＝（-2）2，则a＝-2.其中错误的有（）.

A.4个B.3个C.2个D.1个

商榷：这道选择题是七年级期末考试中某套试卷选择题中的最后一题.首先，这是一种品味不高的选择题型，原因是五个命题只要有一个判断出错，都会影响最后的答案，造成试题信度、效度不高.其次，对于说法②，学生在七年级还没有接触分式，但方程x+2＝中已出现分式，这是不恰当的，现阶段应该回避这种形式.说法④也出现分式.

例5（1）若关于x的方程+1=0是一元一次方程，则m的值为_________.

（2）若关于x的方程（m-2）x|m|-1=5是一元一次方程，则m的值为_________.

（3）若方程（2-m）x2+3mx-（5-2m）=0是关于x的一元一次方程，则m的值为_________.

商榷：这类问题随处可见，不仅在七年级，在后续方程定义的练习中也存在.题目看似渐次变式，由易到难，实质上却是把一元一次方程的概念引向细枝末节，走向繁难.其实，只要学生了解了数学概念，学会识别一元一次方程，知道一元一次方程的一般形式，就不会影响后续学习，没有必要拓展到（2）、（3）两问上.

例6阅读材料：我们知道|x|的几何意义是在数轴上的数x对应的点与原点的距离，即|x|＝|x-0|，也就是说|x|表示在数轴上数x与数0对应的点之间的距离.这个结论可以推广为|x1-x2|表示在数轴上数x1与x2对应的点之间的距离.

问题1：已知|x|＝2，求x的值.

解：容易看出，在数轴上与原点的距离为2的点对应的数为-2和2，即x的值为-2和2.

问题2：已知|x-1|＝2，求x的值.

解：在数轴上与数1对应的点之间的距离为2的点对应的数为3和-1，即x的值为3和-1.

仿照阅读材料的解法，求下列各式中的x的值.

（1）|x|＝3；（2）|x+2|＝4.

商榷：《义务教育数学课程标准（2011年版）》对初中阶段绝对值的学习有明确的要求：“借助数轴理解相反数和绝对值的意义，掌握求有理数的相反数与绝对值的方法，知道|a|的含义（这里a表示有理数）.”然而现实教学和同步测试时，像“例6”这样的习题层出不穷，很多老师热衷于将绝对值“深挖洞”，非得把绝对值的学习引向繁难；其实，思考一下七年级学生刚入初中时学习绝对值的目的就容易发现，绝对值的出现是为了后续有理数的运算服务的，理解这一点后，就知道没有必要将绝对值的训练、考试难度盲目拔高了.

二、进一步的思考

1.多思考数学概念在数学上的地位，努力开发“真正的数学题”

关于“真正的数学题”，章建跃教授认为：“真正的数学题目应该满足一些基本条件，例如：反映数学本质，与重要的数学概念和性质相关，不纠缠于细枝末节，体现基础知识和联系性，解题方法自然、多样，具有发展性，表述形式简洁、流畅且好懂.”上述例1~例4的问题出在“纠缠细枝末节”上，对基本概念的联系性、发展性思考不多.

例7我们把形如ax＋b＝0（a≠0）的方程称为一元一次方程的“一般形式”.以下4个方程：4x＝24；1700＋150x＝2450；0.52x-（1-0.52）x＝80；-x＋4＝0.

（1）上述方程中哪些形式符合“一般形式”，请找出来，并指出a，b的值；

（2）上述方程中哪些不符合“一般形式”，请将它们变形为“一般形式”.

命题意图：关注一元一次方程概念，训练学生学会高效变形.所选的4个方程都来自教材79页第1节.

2.认真研读教材中例习题的价值，构思在此基础上变式生长

江苏刘东升老师在他的《经历问题生成，深刻理解教材——人教八上“每日一题”命题实践与思考》一文中简介了“每日一题”的实践与思考，笔者很受启发，特别是文章强调要重视研读教材中例习题的观点，确实值得倾听，当前很多学案、考卷脱离教材的现象并不是个例，比如上文提及的例1~例6在教材上都难找到对应的原型.作为本文的结束，笔者提供一个由教材例习题出发，构思变式生长的尝试，供研讨.

例8如图1，数轴上的两个点A、B所表示的数分别是a，b.

图1

（1）请写出从图1中能看出的一些信息（至少4条）.

（2）有人从两点间距离公式的角度思考了点A、B之间的距离，请设计一个相关问题，并简答.

（3）若现在图中有A、O、B三个点，进行如下的操作，在每相邻两点间插入1个点，经过5次这样的操作后，数轴上共有几个点？

（4）练习上述问题后，从一个数轴图形出发，能研究这么多的问题，你有什么体会？

三、结束语

命题研究是每个数学教师都应该大力培养的基本功，而不仅仅是出几份试卷，扎实的命题功夫常常可以体现在教学设计上，特别是例习题的改编、生长和追问上.本文选取一些常见考题，并逐题给出商榷的意见，个性化成分多，供批评指正.

1.章建跃.发挥数学的内在力量，为学生谋取长期利益［J］.数学通报，2013（2）.

2.刘东升.经历问题生成，深刻理解教材——人教八上“每日一题”命题实践与思考［J］.中学数学（下），2014（4）.

3.中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

4.许卫兵.简约：数学课堂教学理性回归［J］.课程·教材·教法，2009（5）.