中考命题需谨慎一石三鸟当思量——以2014年滨州市中考数学试题为例

☉山东省滨州市教研室 王文清

☉山东省滨州市北镇中学初中部邢成云

中考命题需谨慎一石三鸟当思量
——以2014年滨州市中考数学试题为例

☉山东省滨州市教研室 王文清

☉山东省滨州市北镇中学初中部邢成云

一、写在前面

大家都知道，命题活动是一件严肃且重要的工作，是一项艰苦的、创造性的脑力劳动，身处其中的每一个人都要经过炼狱般的智能活动，才有可能成就一份好的试题，尤其是中考试题，它除了承载着初中学业水平的认定外，还担负着为高中入学甄别选拔之功能，同时还调适着教学的价值走向（此所谓“一石三鸟”），这就需要我们命制的试题要尽可能地客观、公正、全面、准确.

笔者认为，我们需要对命题人的包容与尊重，因为做这项工作着实不容易，但我们不能对题目包容，不能容忍题目的不适切、不科学、不规范.为了更好地服务于学生、更好地关注学生的可持续发展，需要我们教育同仁的质疑声，唯此，中考命题的方向才不会迷失！

二、命题当需关注

1.板块考查要布局

三大知识板块（课题研究归属到相应板块），在中考题中的考查比例要得当，要精选对学生全面发展和终身发展有用的内容，使得这些数学主干知识、有代表性的内容具有较高的抽样价值，谨防布局偏失带来试题信度、效度的降低.按板块的课时数确定考查的百分数，代数、几何和概率统计依次约为46%、42%、12%，而2014年滨州市的中考试题呈现的比例分别为：代数52.5%（64分），几何38.3%（46分），概率与统计9.2%（11分）.比较可知，比例尚有较大的离差，笔者认为，各大板块的权重分配需要仔细考量，需要探究考查内容领域或知识点的平衡性，以免内容的缺失降低试题的效度.另外，板块内知识点的考查也需要考究，其内容搭配的合理性、考试内容的代表性，都需要关注，而滨州市本年度的中考题，在对数与代数领域内方程体系的考查中，核心知识一元二次方程仅在二次函数（第25题）中作为附属过渡性呈现，且分式方程也见不到，但一元一次方程、二元一次方程组均出现过两次；函数领域内的一次函数也遭遇同样的境况，仅在一个选择题（第9题）里作为干扰支出现过，如此的考查怎不让人质疑！

2.试题命制当严谨

例1（2014年滨州市中考第3题）如图1，是我们学过的用直尺和三角尺画平行线的方法示意图，画图的原理是（）.

A.同位角相等，两直线平行

B.内错角相等，两直线平行

C.两直线平行，同位角相等

D.两直线平行，内错角相等

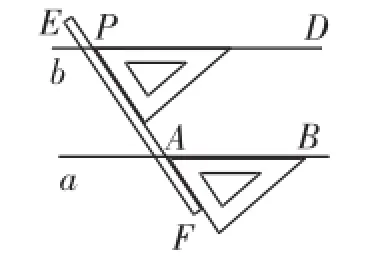
图1

点评：这道题取之人教版七下教材，就教材的语境来说是利用了同位角相等，两直线平行，这无可厚非，但若移植出来变成一道中考题，把答案定为A，还合适吗？选B不可以吗？A、B本来就是等价的！若保持原题考查的意图，可把B项改为：两直线平行，同旁内角互补.

例2（2014年滨州市中考第10题）如图2，如果把△ABC的顶点A先向下平移3格，再向左平移1格到达A′点，连接A′B，则线段A′B与线段AC的关系是（）.

A.垂直B.相等

C.平分D.平分且垂直

图2

点评：本题的选择支有包含关系，A、C、D三个答案都可以认为是正确的.再进一步说，“平分”的说法不确切，是谁平分谁？实际上是互相平分，严格来说，原题的选项可以修改为：

A.垂直但不互相平分B.相等

C.互相平分但不垂直D.互相平分且垂直

例3（2014年滨州市中考第11题）如图3，在Rt△ACB中，∠C=90°，AB=10，sinA=，cosA=，tanA=，则BC的长为（）.

图3

A.6B.7.5C.8D.12.5

点评：典型的条件过剩，给定一个三角函数值就足够了，却弄上三个，显然有两个冗余条件，考查目的何在？让人实在是费解！我们知道，由于条件过剩，往往会使题目的严谨性大打折扣，给考生造成无谓的混乱.有的学生看到条件没有派上用场，可能要反复地琢磨，无端地浪费了考场上的宝贵时间，干扰了学生的正常思维，如此之偏失造成了试题外部认知负荷的加大，这理应是与考查初衷相悖的.但所幸的是，这一过剩条件并没有形成结果的抵触，不论从哪一个三角函数表达式入手解答，获得的答案一致.建议去掉其中任意两个三角函数表达式！

3.偏离考纲为哪般

第12题实际是对不等式组应用的考查，而不等式组的应用在山东省滨州市的《考试说明》里是明令不考的，却在考题中出现了，内容如此偏离考纲降低了试题的效度.

例4（2014年滨州市中考第12题）王芳同学到文具店购买中性笔和笔记本，中性笔每支0.8元，笔记本每本1.2元，王芳同学花了10元钱，则可供她选择的购买方案的个数为（两样都买，余下的钱少于0.8元）（）.

A.6B.7C.8D.9

4.“拿来主义”要不得

作为平时对学生理解知识、应用知识的检测，选用成题倒也无妨，但若是对承载着多重功能，尤其是关乎升学这一敏感的话题时，再简单的拿来主义，选用成题、陈题实不应该！它的出现会严重影响试卷有效考查学生的真实水平的目的，降低了试卷的效度，它会带来新的不公平，给投机钻营者、机械训练者、押题猜题者带来上乘的收益，会加剧“题海”之战，误导教学的价值走向.今年滨州市的中考题就有这个嫌疑，我们抛开选择题不论，从填空题算起，就有以下题目不加改造地照搬照抄：第14题直接照搬2012年滨州市的第15题；第17题只字未动，原本照搬2013年宁夏第13题；第21题抄袭2011年枣庄市第23题；第22题为2012年黄冈市第19题的小改造；除此之外，第19题的自选与滨州市去年的考题如出一辙.

这种赤裸裸的抄袭现象，似乎已名正言顺，不得不引起学术界及有关行政部门的高度重视，否则，负面的影响足以扰乱命题的“局”，小则让一些有真才实学并脚踏实地、孜孜以求的命题者心理失衡，大则殃及学生未来.

坚持试题的原创性是保证中考评价公平性的积极而有效的举措.注重原创，让猜题、押题没有市场，才会真正形成积极的教学导向，才会引领教学健康发展.

5.自选何以显其能

近两年，滨州市在题型设计上，开始关注学生个性化展示学业水平，通过设置自选题，理论上讲，可增加考试对学生的适切性和选择性.学生可以根据自己学习的认知特点，选择适合自己的题目进行解答，在一定程度上发挥了学生的个性化水平，有利于提高考试的信度.这种自选平台的搭建，应该说是人性的表现，也是公平的体现.可惜的是滨州市的自选题并没关注到个性差异，第19题中的两个自选题如出一辙，一个解方程组、一个解方程，同归属于一个领域，在同知识点处周旋，可以说是为形式而设，如此选作，意义何在？难道就是为了一个响亮的名字而已，更让人不解的是今年的这个自选题基本照搬了滨州市去年的自选题，两年并无二致，让人扼腕！如此的坚守是否背离了自选的初衷？

笔者之见，是否兼顾不同的领域，给个性差异的学生以个性的关注.比如最简单的命题形式，一个考查代数内容、一个考查几何内容.

例5（2013年滨州市中考第19题）（请在下列两个小题中，任选其一完成即可）

例6（2014年滨州市中考第19题）（请在下列两个小题中，任选其一完成）

6.考查目的伪落实

A.0～1之间B.1～2之间

C.2～3之间D.3～4之间

例8（2014年滨州市中考第13题）计算-3×2+（-2）2-5=_________.

点评：一个“估计”、一个“计算”都会在计算器进入考场的背景下失去考查的目的，例7的估计是考查无理数的估算的，例8的“计算”是考查有理数混合运算的，若学生拿起计算器就可以一按了之！使试题达不到命题者预期的考查目的和教育价值，不可避免地降低了考试的效度.因此，在计算器进入考场的前提下，题目怎么命，需要我们深入思考！若考查运算，可在算式中加入根式运算或大指数参与运算等，并要求不求近似值；至于估算问题，笔者尚未想到合适的方法，不过可以尝试借鉴国外（如澳大利亚）的方法，把数学分成两部分考试，一部分禁用计算器，一部分可用计算器，这样可以有效避免计算器带来的试题效度问题.

7.压轴之题需斟酌

例9（2014年滨州市中考第25题）如图4，在矩形ABCD中，AB=20，BC=10，点P为AB边上一动点，OP交AC于点Q.

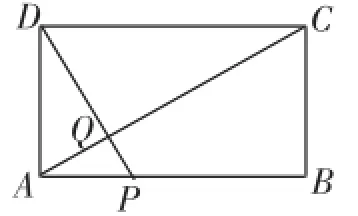
图4

（1）求证：△APQ∽△CDQ.

（2）P点从A点出发沿AB边以每秒1个单位长度的速度向B点移动，移动时间为t秒.

①当t为何值时，DP⊥AC？

②设S△APQ+S△DCQ=y，写出y与t之间的函数解析式，并探究P点运动到第几秒到第几秒之间时，y取得最小值.

限于篇幅，我们只展示最后一小问的解答：

②设△ADP的边AP上的高为h，则△QDC的边DC上的高为10-h.

探究：

t=0，y=100；t=1，y≈95.48；t=2，y≈91.82；t=3，y≈88.91；t=4，y≈86.67；t=5，y=85；t=6，y≈83.85；t=7，y≈83.15；t=8，y≈82.86；t=9，y≈82.93；t=10，y≈83.33；t=11，y≈84.03；t=12，y=85；t=13，y≈86.21；t=14，y≈87.65；t= 15，y≈89.29；t=16，y≈91.11；t=17，y≈93.11；t=18，y≈95.26；t=19，y≈97.56；t=20，y=100.

观察数据知：

当0≤t≤8时，y随t的增大而减小；

当9≤t≤20时，y随t的增大而增大.

故y在第8秒到第9秒之间取得最小值.

点评：解析式的探求暂且不论，单看这个探究过程的重复计算量，这是在干什么？考查目的何在？作为初中学段非基本初等函数的未知函数类型，如何探索其变化趋势是核心内容吗？在这里考查学生的能力是否得当？就是用计算器来完成这个题目的计算会用去多少时间？话又说过来，若离开计算器去计算，会出现什么现象？从抽样统计来看，这个小题的区分度近乎于0，很显然，这相当于一个费题！另外，不看题目在考查中的效用价值等，就这个题而言，也是不科学的、有问题的.试看“并探究P点运动到第几秒到第几秒之间时，y取得最小值”，这句话什么意思？既然是“y取得最小值”，那应该对应着一个固定的时刻，怎么会是“第几秒到第几秒之间”这样的区间呢？再者，“第几秒到第几秒之间”的说法是不确切的，答案给定的是第8秒至第9秒，那第8秒到第10秒不可以吗？进一步说，第0秒到第20秒不行吗？可见，本题是经不起推敲的，其科学性值得质疑！其实本题可以通过高中的基本不等式“a+b≥2”求出当t=20-20秒时，函数取得最小值为200-200.而2020在第8秒与第9秒之间，答案可定.很显然，这道题应用高中知识的常规方法很容易解决，而利用初中知识的话技巧性很高，如此的考查方向，对初中数学教学也是极为不利的.

基于本小题设问的不合理，难于实现设计的意图.若要达到原初的设计意图，可以把设问修改为“并探究P点运动到第n（n为自然数）秒到第（n+1）秒之间时，y能取到最小值”，增强其约束力，使之明确化、具体化，就不会有异议了.纵然如此，这一道压轴偏离了核心内容、核心思想方法及能力的考查，需要调整.

8.尺规作图何时归

通过查阅滨州市近4年中考题，4份试卷没见到一个作图题，我们都知道，尺规作图题是考查学生几何直观能力的题目，是落实三类语言（文字、符号、图形）转换及图形变换的优质载体，是实现图形运动的极佳手段，尤其是2011年版的新课程标准，对尺规作图做了调适，恢复了它的应有地位，可以说实至名归，较之课改初对尺规作图的要求提高了；同时，将“几何直观”正式列为“课程内容”的核心概念，增加了多处有关借助于几何图形了解或理解概念，以及运用几何作图解决问题的内容目标.但今年滨州市的中考题仍然没有走出这个命题“惯性”.如此考查学生图形变换的好载体，为何千呼万唤不出来，真匪夷所思！

三、启示与建议

1.三个利于当须记，最是创新要坚守

中考命题，作为初中学段终端性试题的命制，应该承载着初中数学新课程的理念，赋有带动和促进教学方式的转变，有利于引导教学，引领师生从“题海”中解脱出来，真正地回归教材、强化课堂、涵养思维，改进教学，成就自我；有利于学生展示自己的水平、形成继续学习所需要的素养和能力，落实好以学生为本；有利于高中入学的选拔与甄别，落实好衔接与发展需求.创新是命题的生命线，没有创新，试题就难保客观公平，剽窃抄袭不道德，抱残守缺要不得！

2.数学严谨岂能忘，命题严谨不可丢

一道优质、科学的数学题，题目本身的结构和叙述要满足合理性、严谨性和清晰性.逻辑上要严密，不能为了达到降低试题难度的目的，而给出过多的条件，我们知道，某个条件给定，相对应的一系列条件往往也随之确定，如果命题者只是主观臆断，没有经过反复推敲，给出自相矛盾的多余条件，虽然问题是可解的，但得出的结论却是荒唐的.因此，题目的条件是一个不多、也一个不能少，且各种条件之间又不能存在矛盾冲突，即满足充分性、相容性、独立性；另外，条件与结论也要具有相容性.严谨与科学是命题的底线，以学生的发展为本是命题的基点，基于此，命题者命制试题要怀敬畏心、责任心，一定要字斟句酌、精雕细刻、精益求精、反复打磨，要虔诚地面对每一道题，不要拿来就用，要多研究、多思考，力避因试题陈述与呈现的不合理、不规范、不严密、不准确等带给学生理解上的歧义或无谓的阻滞，使学生遭遇无可挽回的损失，谨防我们的命题偏失害了学生、误导了教师的教学，把数学引向不归路.

四、结束语

“一石三鸟”量力，“三驾马车”齐驱，不折腾、不跟风，坚守创新，锐意进取，走出中考评价的新天地！2014年度滨州市的中考试题是比较有代表性的“问题”试题，命题常见的问题大都于此暴露无遗，个人陋见未免偏颇，恳请指正！

1.韩继琼.一道讲错了几年的中考题［J］.中学数学（下），2013（9）.

2.卧松.计算器不能代替心算［N］.中国教师报，2005-11-16（4）.

3.许云勇.计算器对学生计算能力影响的分析［D］.武汉：华中师范大学，2008.