广义剪切活动准则*
童亨茂,陈正乐, 刘瑞珣
①中国石油大学(北京)油气资源与探测国家重点实验室,北京 102249;②中国地质科学院地质力学研究所,北京 100086;③北京大学地球与空间科学学院,北京 100871
广义剪切活动准则*
童亨茂①†,陈正乐②, 刘瑞珣③
①中国石油大学(北京)油气资源与探测国家重点实验室,北京 102249;②中国地质科学院地质力学研究所,北京 100086;③北京大学地球与空间科学学院,北京 100871
针对经典的剪切破裂准则(Coulomb-Mohr准则和以Byerlee律为代表的滑动摩擦律)存在局限,在Coulomb-Mohr准则和Byerlee律的基础上,从产生剪切破裂的物理本质出发,应用先存构造活动性准则和活动趋势分析理论,提出 “广义剪切活动准则”。该准则可以用来定量判断任意介质、在任意三轴应力状态下、任意方位界面(包括先存薄弱面和非薄弱面)发生剪切活动的可能性,并把Coulomb-Mohr准则从均匀介质扩展到有先存构造的非均匀介质,从临界应力状态扩展到任意应力状态,把Byerlee律为代表的滑动摩擦律从二维应力状态扩展到任意三轴应力状态,具有广阔的应用前景。
剪切活动;先存构造;Coulomb-Mohr准则;Byerlee律;广义剪切活动准则
断层是岩石圈的最基本的构造要素之一[1]。地球上几乎所有的内动力地质作用和大部分外动力地质作用都与断层有关,同时矿产资源(如石油和天然气)和地质灾害(如地震、火山、山体滑坡等)都直接或间接地与断层相关[1-2]。
断层作用的物理本质是岩石的剪切活动。岩石发生剪切破裂的经典准则是Coulomb-Mohr准则[1]。然而,Coulomb-Mohr准则只适用于均匀介质,产生的断层是方位优选的[3],而且只能预测破裂发生前的瞬间趋势,不能用来分析破裂发生后的递进变形过程。为了克服均匀介质的限制,不同学者先后提出了沿先存构造面滑动的摩擦滑动定律[4-6]和滑动趋势分析理论[7],但这些理论依然不能很好地解决自然界非均匀介质断层作用的力学机理问题。
本文在Coulomb-Mohr准则的基础上,从产生剪切破裂的物理本质(作用在介质潜在剪破裂面上的剪应力克服该界面上的内聚力和(内)摩擦力,即可产生剪切破裂)出发,应用先存构造活动性准则(activation criterion of pre-existing fabric)[8]和活动趋势分析理论(theory of activation tendency analysis)[9],提出了适用于任意应力状态、任意介质的脆性剪切活动准则,即“广义剪切活动准则”,并进一步讨论与经典剪切破裂准则的关系及应用前景。
1 Coulomb-Mohr准则
岩石发生剪切破裂的基本准则是Coulomb-Mohr准则[1,6]。
Coulomb剪切破裂准则是Coulomb于1776年提出的[10]。该准则认为:岩石发生剪切破坏不仅与作用在截面上的剪应力有关,而且还与作用在该截面上的正应力有关,可以用下式表示[1-2]:

其中t为临界剪应力,σn为该截面上的正应力,μ为介质的内摩擦系数(常数)。式(1)在t-σn坐标系中为一直线(图1),称为库仑剪破裂线, μ为该直线的斜率。若μ用库仑剪破裂线的倾斜角φ表示,则μ= tanφ,φ为岩石的内摩擦角。发生Coulomb剪破裂的临界应力状态被称为Coulomb应力状态。
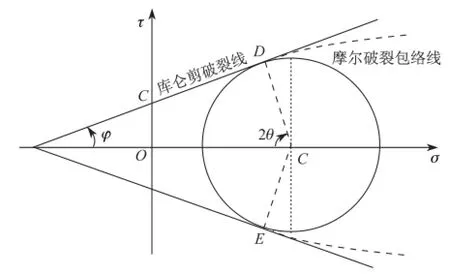
图1 Coulomb-Mohr准则的摩尔圆图解[1-2]
Mohr剪切破裂准则认为,内摩擦系数μ及内摩擦角φ并不是一常数,它与σn相关,一般随着σn的增大而减小。这样,摩尔剪切破裂线是曲线,被称之为摩尔破裂包络线(图1)[1-2]。
Coulomb准则针对均匀介质[3]。Anderson根据Coulomb剪切破裂准则,指出均匀介质的岩石在应力作用下发生的剪切破裂是方位优选的,即剪切破裂面与最大主压应力轴σ1的夹角(剪裂角)等于±(45°-φ/2)(其中φ为摩擦角),并与中间主应力轴σ2平行,是一对共轭的破裂面[3]。在此基础上,他又进一步提出了Anderson断层模式,成为构造地质学的世纪经典理论,至今还产生重要影响[10]。但该断层模式基于均匀介质,实际应用中具有显著的局限性[8,11]。
2 滑动摩擦律(Byerlee律)
基于Coulomb-Mohr准则的 Anderson模式被广泛深入应用后,发现有很多实际地质现象无法用Anderson模式来解释,主要存在三个方面的问题[8,11]。其中之一,它不符合沿先存构造面上滑动的断层作用。
Anderson断层模式假定地质体是均匀介质,预测的断层是方位优选的,只与主应力的方位有关,与其他(如先存构造面)无关。然而,实际地质体是非均质的。
地质体的非均质性存在多种形式,如沉积盆地中沉积岩的层理、基底中先存断裂构造、面理等。砂箱实验研究表明,在沉积盆地中,先存构造(主要是先存断裂)对非均质性的影响一般最为显著,是造成地质体非均质的主导因素[8,12]。一般情况下(如露头尺度),地壳岩石的非均质性是很强的,这是造成Anderson模式存在局限,无法很好地解释自然界断层作用现象的根本原因。
为了克服上述问题,先后提出了滑动摩擦律[4-6,13-14]和滑动趋势分析理论[7]。摩擦律认为,先存断裂在地应力作用下,当作用在先存断裂面上的剪应力克服其内聚力和摩擦力后,先存断裂可以重新活动[4-5,14],其中最著名的是在实验基础上提出的Byerlee 律[5],可以用下式表示:

其中tW为临界剪应力,CW为先存断裂面的内聚力,σn为先存断裂面上的正应力,μW为先存断面上的摩擦系数。
滑动摩擦律提出沿先存构造面滑动的断层作用克服了Anderson断层模式中均质体的假设和斜向滑动的问题[4-5,13],但这些模型都局限于二维应力分析[7]。滑动趋势分析理论[7]把沿薄弱面的摩擦滑动分析从二维扩展到三维,在三轴应力已知的情况下(主应力值确定,方向直立或水平,即Anderson应力状态),定量分析了先存薄弱面发生活动的可能性,并用来分析不同先存构造地震活动的可能性。但该模型只考虑Anderson应力状态(一个主应力轴直立),而忽略了薄弱面的内聚力,也没有考虑岩石内摩擦系数的变化[9],因此也具有一定的局限性。
滑动摩擦律在一定程度上克服了Anderson模式的局限性,但也没有从根本上解决自然界复杂介质条件下断层作用的力学机制问题。
3 剪切活动的物理本质与广义剪切活动准则
3. 1 剪切活动的物理本质
分析Coulomb-Mohr准则和Byerlee律可以看出,不论是均匀介质还是非均匀介质,产生剪切活动的物理本质是共同的,即作用在界面上的剪应力只要能克服该界面上的内聚力和(内)摩擦力,即可产生剪切活动。本文使用“剪切活动”而非“剪切破裂”一词,是因为沿失去内聚力(已经破坏)的构造面发生剪切活动不需要再发生剪切破坏,即“剪切活动”存在两种情况:①产生剪切活动的潜在界面是有内聚力的,则剪切活动通过剪切破坏而产生,需要克服内聚力和内摩擦力;②产生剪切活动的界面无内聚力(如先存断裂面),则剪切活动只需克服界面的摩擦力即可产生。
这样,从剪切活动的物理本质出发,对于任意介质中的任意界面,发生剪切活动的临界剪应力[tn]可以用下式表示:

式中, [tn]为沿界面的临界剪应力,CP、μP和σn分别为该界面的内聚力、(内)摩擦系数和正应力。当界面没有内聚力时,CP取0。
3.2 剪切活动趋势因子及其数学表达
通过上述剪切活动物理本质的分析,对任意介质中的任意界面,定义一参数 fs称之为剪切活动趋势因子,用来描述任意界面发生剪切活动的可能性。fs可表示为

式中,tn为沿界面的剪应力,[tn]为沿该界面产生剪切活动时的临界剪应力。很显然,当 fs=1时,该界面处于临界剪切活动状态;当 fs>1时,处于已活动状态;当 fs<1时,处于稳定状态。
结合式(3)和(4),得到
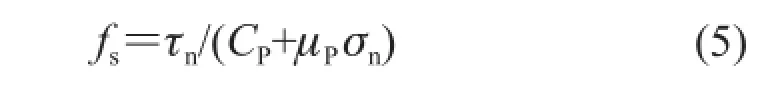
在任意三轴应力状态下,童亨茂等[8]给出了σn和tn的定量计算公式[8]:

结合式(5)~(8),在任意三轴应力状态下,得到剪切活动趋势因子 fs的计算公式:

其中σ1、σ2和σ3分别为最大、中间和最小主压应力,θ为界面与σ1的夹角,α为界面在σ2-σ3平面上的交线与σ3的夹角。界面的地理方位(如倾向和倾角)与θ和α之间的关系可以通过坐标转换来建立[9]。
很容易看出,这里的剪切活动趋势因子fs和童亨茂等[8]提出的先存构造活动性准则中的先存构造活动性系数 fa具有相同形式的表达式,只是 fa针对的是先存构造面,而 fs针对任何界面。用式(9)可以定量计算在任意三轴应力状态下、任意方位界面(包括先存薄弱面和非薄弱面)发生剪切活动的可能性。
3.3 剪切活动趋势因子在摩尔空间中的表达
据式(9),剪切活动趋势因子 fs与应力状态(3个主应力值)、界面相对主应力的方位(θ和α)及其界面的力学性质(CP,μP)有关,但由于 fs的计算公式(式9)比较复杂,不方便对各影响因素进行定量分析。然而,利用Tong和Yin[9]提出的“摩尔空间”图解,则可以很直观地解决这一问题,也就是可以很直观地分析剪切活动趋势因子fs与应力状态、界面方位和界面力学性质等之间的定量关系。
在任一应力状态下,应用摩尔空间可以十分直观地表达任一确定方位界面的正应力、剪应力以及界面的力学性质(图2)[15]:①按照界面的方位(θ和α)找到该界面在摩尔空间中的极点,该极点的横坐标和纵坐标分别对应界面上正应力(σn)和剪应力(tn);②界面的临界剪切活动线(式3的图形表达)的起点(CP, 0)决定于界面的内聚力 CP,斜率决定于(内)摩擦系数μP。这样,当应力状态(决定摩尔空间)、界面的力学性质(决定界面的临界活动线)和界面的方位(决定界面在摩尔空间中极点的位置)确定时,应用摩尔空间就可以十分方便、直观地表达和预测任一界面的剪切活动性(图2)。剪切活动趋势因子 fs由其极点P(σn, tn)与其相对应的临界活动点(σn,)的相对位置决定,等于tn和的比值(图2),即当界面的极点位于:①临界剪切活动线上时(如图2中的P3),界面处于临界活动状态;②临界剪切活动线之外时(图2中有横线的黄色区域,如P1),界面已经活动;③临界剪切活动线之内(图2中没有横线的黄色区域,如P2),界面处于稳定状态。这种判别方法适用于任何界面(包括薄弱面和非薄弱面):当界面为非薄弱界面时,临界剪切活动线为Coulomb-Mohr包络线;当界面为先存薄弱面时,临界剪切活动线为先存构造活动线(如图2中的a和a′)[8]。

图2 “摩尔空间”及剪切活动趋势因子fs的表达(据文献[15]修改)(σ1-σ3、σ1-σ2和 σ2-σ3三个摩尔圆以及黄色区域构成“摩尔空间”;绿色虚线和粉色虚线为界面方位角θ和φ的等值线;a和a′为先存构造活动线;P1、P2和P3分别为3个先存构造界面(其力学性质CW、μW一致)在摩尔空间中的极点(σ, t)、(σ, t)和(σ, t),tW、n1n1n2n2n3n3n1tn2W和分别为对应的临界剪应力,对应的剪切活动趋势因子fs分别为fS1>1.0、fS2<1.0和 fS3=1.0;CW为先存构造界面的内聚力;A和A′为Coulomb剪切破裂点)
3.4 广义剪切活动准则及其与Coulomb-Mohr准则、Byerlee律之间的关系
3.4.1 剪切活动趋势因子 fs算式在实际地质体中的适用性
从前面的分析可以看出,剪切活动趋势因子fs的算式(式9)理论上适用于任何介质,但式(9)隐含了两个条件:计算区域内的应力场是均匀的;界面是一平面,而且其力学性质是一样的。只有包含平面(板)状先存构造的非均匀介质(先存构造为平面(板)状,且不同位置的力学性质一致;母质为均匀介质),才能满足上述两个条件。那么,式(9)是否适用于实际的非均匀地质体呢?
研究表明,先存构造对地质体非均质性的影响最为显著[8,12]。Morley等[16]把先存构造分为分隔性构造和透入性构造:前者是指介质中存在一个截然的破裂面,相当于先存断层,内聚力很小或为零;后者是由一系列弥漫性构造组成,力学性质上为一相对薄弱带,内聚力小于周围介质。
按照有限单元的思想,任何类型的实际非均匀地质体,只要进行有限单元的划分,都可以看作是含平面(板)状先存构造的介质和均匀介质的组合体。例如:砂泥岩互层、层内均匀的沉积岩,可以看作是有先存薄弱带(泥岩)的均匀砂岩;复杂形态的先存断裂面,只要把断面分割成足够小的有限单元,单元内的断面可以看作是平面;被不规则岩脉侵入的岩体,不管侵入接触的边界多么复杂,只要把边界附近的岩体分割成足够小的有限单元,单元内就可以看作是有分隔性先存构造(侵入接触面)的均匀岩体。
从上面的分析可以看出,任何实际的非均匀地质体,从力学上均可以看作是含平面(板)状先存构造(薄弱带)的均匀介质(如含一条平面状断层的均匀地质体)及其组合体。因此从理论上说,式(9)适用于任何实际的地质体。
3.4.2 式(9)与Coulomb-Mohr准则的关系
很容易验证,当Cp=C,μP=μ,即在均匀介质的情况下,若fs=1(发生临界剪切活动),式(9)可以简化成式(1),即Coulomb-Mohr准则。这样,Coulomb-Mohr准则是式(9)在均匀介质和临界剪切活动情况下的端元。
Coulomb-Mohr准则是式(9)端元的情况还可以用摩尔空间来直观地说明。图2中的摩尔空间代表临界Coulomb应力状态,大摩尔圆与Coulomb剪破裂线相切,切点为A和A′。在此摩尔空间中,极点位于先存构造活动线(a和a′)上及其以外区域(图2中有横线的黄色区域)的先存构造界面(CW、μW均一致)都达到了剪切活动的条件(fs≥1),即在临界Coulomb应力状态下,存在无数个潜在的先存薄弱面满足剪切活动条件。随着CW的变大,先存构造活动线(图2中的a和a′)向外移动,满足剪切活动条件的区间(图2中有横线的黄色区域)逐渐变小;当CW=C,且μP=μ,即有先存构造的介质转化为均匀介质后,该区间退缩成两个点(如图2中的A和A′,代表一对共轭剪切破裂),转化为Coulomb-Mohr准则(fs=1),同时先存构造活动线(如图中的a和a′)转化为Coulomb-Mohr剪破裂包络线。这样,式(9)把Coulomb-Mohr准则从均匀介质扩展到有先存构造的非均匀介质,从临界应力状态扩展到任意应力状态。同时,式(9)也揭示了按Coulomb-Mohr准则产生的剪破裂为方位优选(optimal)[3]的物理本质:在均匀介质所有方位的界面中,只有方位优选的界面才能达到临界剪切活动的条件fs=1。
3.4.3 式(9)与滑动摩擦律的关系
很容易验证,滑动摩擦律的代表Byerlee律是式(9)在二维应力状态下(界面与中间主应力σ2轴平行),先存薄弱面处于临界剪切活动状态(fs=1)的端元。在图2的摩尔空间中,Byerlee律代表先存构造活动线a和a′和大摩尔圆相交的4个点。这表明式(9)把以Byerlee律为代表的滑动摩擦律扩展到任意三轴应力状态。
前面的分析表明,剪切活动趋势因子 fs的算式(9)一方面把经典的剪切破裂准则Coulomb-Mohr准则和Byerlee律统一起来,并把它们作为其中的端元;另一方面,理论上式(9)适用于任何非均匀介质和任意应力状态。为此,称剪切活动趋势因子 fs的算式(9)为“广义剪切活动准则”,可以定量判断任意介质、在任意三轴应力状态下、任意方位界面(包括先存薄弱面和非薄弱面)发生剪切活动的可能性。
4 广义剪切活动准则的应用前景分析
4.1 断层作用研究中的应用
断层作用的物理本质是地质体沿界面发生剪切活动。Anderson于1905年基于Coloumb准则,建立了岩石圈在Anderson应力状态(其中一个主应力直立)和均匀介质的假定条件下的断层作用模式,即Anderson断层模式[3]。但实际地质体存在不同程度的非均质性,造成Anderson模式存在局限,无法很好地解释自然界断层作用现象[8]。由于广义剪切破裂准则适用于任何非均匀介质和任意应力状态,这样,基于广义剪切活动准则建立的“广义断层模式”(将在另文中介绍)适用于岩石圈中的任意应力状态和任何类型的地质体,可以合理地解决自然界的各种断层作用现象,使得断层作用的理论模型更加符合地质实际,具有更好的理论指导作用。
4.2 其他方面的应用
理论上,广义剪切活动准则可以应用到与剪切活动相关的各种作用的分析研究中,如边坡稳定性分析和预测,断层的地震活动性分析,油气开发过程中的注水、注气和热采等能否导致断层的重新活动(断层的重新活动导致钻井和套管的破坏)的研究分析,隧道(或坑道)开挖时断裂的稳定性分析,以及与大型工程地基相关的断层稳定性分析等。具体的分析方法不在这里一一详述。
5 讨论
广义剪切活动准则隐含了两个条件:①计算区域内的应力场是均匀的;②界面是一平面,而且其力学性质是一致的。在要求十分精确的情况下,只有把非均匀介质分割成足够小的微元后,才能达到广义剪切活动准则的应用条件。
由于地质体的非均质性和地质作用的复杂性,到目前为止,还未有任何一个理论能精确分析和预测地质作用过程,但这并不影响相关地质理论的应用和价值。适当的误差是允许的,对广义剪切活动准则也是如此。任何理论应用均需对实际地质体和地质作用过程作适当和必要的简化,但只要新的理论所对应的模型相对更加符合地质实际,得到的认识更为深化,预测相对更为准确,就能体现该理论的意义和价值。例如:①自然界实际的断层面都是曲面,但并非需要分割成无限小后才能看作是平面,而是综合考虑相关数据的误差情况和工作需要后,把断层面分割成若干段落,每个段落的断面即可认为是平面,其内的应力场可以认为是均匀的,即可达到广义剪切活动准则的应用条件。②在岩石圈应力状态下,由于重力的作用,主应力值随深度是不断变化的,应力场必然是非均匀的;但如果只分析断层的方位,在介质是均匀的情况下,应力场也可以被看作是均匀的[3]。如童亨茂等[9,18]在砂箱实验时,发现砂箱内按均匀应力场预测得到的结果与模拟实验结果具有惊人的一致性。
当然,在条件具备的情况下,单元分割得越精细,用广义剪切活动准则预测的结果就相对越准确。如一条断层面上的应力分析和力学性质分析达到很精细的情况下,就可以应用广义剪切活动准则实现对断面上不同区域的剪切活动趋势作出更为精细的预测结果。
值得注意的是,剪切活动一旦产生,剪切面附近就会产生应力降,形成局部应力场[17-20]。另外,在剪切活动过程中(断层作用过程),随着地质体的变形和变位,局部应力场也会不断发生变化[18]。因此,应力和应变是紧密关联的两个方面,即应力导致应变,应变又引起应力的变化,构成应力-应变体系(stress-strain system)。在递进变形过程中,应力场的演化过程十分复杂,其研究目前还刚起步。广义剪切破裂准则是联系应力和剪切应变(断层作用)的桥梁,而褶皱变形往往与断层作用紧密相关。随着观测资料的不断精细(如高精度三维地震资料),变形结果(构造几何特征)的可观测性和变形过程(构造的运动学过程)的可解析性不断增强,广义剪切破裂准则理论有望在递进变形过程中应力场演化这一研究领域发挥重要作用。
6 结论
广义剪切活动准则,从理论上可以定量判断任意介质、在任意三轴应力状态下、任意方位界面(包括先存薄弱面和非薄弱面)发生剪切活动的可能性,并可对不同区域进行对比分析。广义剪切活动准则把Coulomb-Mohr准则从均匀介质扩展到有先存构造的非均匀介质,从临界应力状态扩展到任意应力状态,以及把Byerlee律为代表的滑动摩擦律从二维应力状态扩展到任意三轴应力状态。
在实际应用中,综合考虑相关数据的误差情况和工作需要,把要研究的界面(如断层面)分割成若干段落后,认为满足①计算区域内的应力场是均匀的;②界面是一平面,而且其力学性质是统一的这两个条件后,即可应用广义剪切活动准则,来定量分析和预测界面不同段落发生剪切活动的可能性。
(2015年9月23日收稿)
[1] TWISS R J, MOORES E M. Structural geology [M]. New York: W. H. Freeman and Company, 1992: 532.
[2] 徐开礼, 朱志澄. 构造地质学[M]. 北京: 地质出版社, 1998: 270.
[3] ANDERSON E M. The dynamics of faulting [M]. 2nd ed. Edingburgh: Oliver and Boyd, 1951.
[4] BOTT M H P. The mechanics of oblique slip faulting [J]. Geol Mag, 1959, 96: 109-117.
[5] BYERLEE J D. Friction of rocks [J]. Pure and Application Geophysics, 1978, 116: 615-626.
[6] JAEGER J C, COOK N G W. Fundamentals of rock mechanics [M]. 3rd ed. London: Chapman and Hall, 1979: 593.
[7] MORRIS A, DAVID A F, HENDERSON B. Slip-tendency analysis and fault reactivation [J]. Geology, 1996, 24: 275-278.
[8] TONG H, CAI D, WU Y, et al. Activity criterion of pre-existing fabrics in non-homogeneous deformation domain [J]. Science China (Earth Sciences), 2010, 53(8): 1115-1125.
[9] TONG H, YIN A. Reactivation tendency analysis: A theory for predicting the temporal evolution of preexisting weakness under uniform stress state [J]. Tectonophysics, 2011, 503: 195-200.
[10] CÉLÉRIER B. Seeking Anderson’s faulting in seismicity: a centennial celebration [J]. Reviews of Geophysics, 2008, 46: 1-34.
[11] 童亨茂. “不协调伸展”作用下裂陷盆地断层的形成和演化模式[J]. 地质通报, 2011, 29(11): 1606-1613.
[12] 童亨茂, 孟令箭, 蔡东升, 等. 裂陷盆地断层的形成和演化——目标砂箱模拟实验与认识[J]. 地质学报, 2009, 83(6): 759-774.
[13] WALLACE R E. Geometry of shearing stress and relation to faulting [J]. J Geol, 1951, 59: 118-130.
[14] MCKENZIE D P. The relation between fault plane solutions for earthquakes and the directions of the principal stresses [J]. Bull Seismol Soc Am, 1969, 59: 591-601.
[15] 童亨茂, 王建君, 赵海涛, 等. “摩尔空间”及其在先存构造活动性预测中的应用[J]. 中国科学: 地球科学, 2014, 44(9): 1948-1957.
[16] MORLEY C K, HARANYA C, PHOOSONGSEE W S. Activation of rift oblique and rift parallel pre-existing fabrics during extension and their effect on deformation style: examples from the rifts of Thailand [J]. J Structural Geology, 2004, 26: 1803-1829.
[17] GUDMUNDSSON A, SIMMENES T H, LARSEN B, et al. Effects of internal structure and local stresses on fracture propagation, deflection, and arrest in fault zones [J]. J Structural Geology, 2010, 32: 1643-1655.
[18] TONG H, KOYI H, HUANG S, et al. The effect of multiple preexisting weaknesses on formation and evolution of faults in extendedsandbox models [J]. Tectonophysics, 2014, 626: 197-212.
[19] MORLEY C K, SEUSUTTHIY G K. Fault superimposition and linkage resulting from stress changes during rifting: Examples from 3D seismic data, Phitsanulok Basin, Thailand [J]. J Structural Geology, 2007, 29: 646-663.
[20] YIN A. Mechanics of monoclonal systems in the Colorado plateau during the Laramide orogen [J]. J Geophys Res, 1994, 99: 22043-22058.
Generalized shear activation criterion
TONG Hengmao①, CHEN Zhengle②, LIU Ruixun③
①Key National Laboratories of Oil and Gas Resources and Exploration, China University of Petroleum, Beijing 102249, China;②Institute of Geomechanics, Chinese Academy of Geological Sciences, Beijing 100086, China; ③School of Earth and Space Sciences, Peking University, Beijing 100871, China
There are some limitations in classic shear fracture criteria such as Coulomb-Mohr criterion and sliding friction law represented by Byerlee law. On the base of Coulomb-Mohr criterion and Byerlee law, starting from the physical nature of shear fracture, and applying the activation criterion of pre-existing weakness and the theory of activation tendency analysis, a generalized shear activation criterion is proposed. The criterion can be used to quantitatively determine the probability of shear activation for any medium, any stress state, any orientation plane. It extends not only Coulomb-Mohr criterion from homogeneous media to inhomogeneous media with pre-existing weakness, but the sliding friction law represented by Byerlee law from 2D stress state to any triaxial stress state, and shows broad application prospects.
shear activation, pre-existing weakness, Coulomb-Mohr criterion, Byerlee law, generalized shear activation criterion
(编辑:沈美芳)
10.3969/j.issn.0253-9608.2015.06.007
*国家自然科学基金 (41272160、40772086) 和国家油气重大专项(2011ZX05006-006-02-01、2011ZX5023-004-012)资助
†通信作者,E-mail:tong-hm@163.com

