普通高中教育经费支出效率研究——基于我国中部省份的数据

朱茂勇

（南京师范大学 教育科学学院，江苏 南京210000）

长期以来，学者们把研究重点都集中在义务教育和高等教育经费的使用上，往往忽视了我国普通高中教育经费使用效率这一领域。随着普通高中教育经费收入的不断增加，探讨普通高中教育经费的使用效率问题至关重要。考虑到部分西部地区省份普通高中教育经费领域数据的缺失，故本研究的样本我们只选择了我国中部地区省份。我们利用DEA规模报酬可变模型和二次相对效率法对中部地区普通高中教育经费支出效率进行了分析，从而精确计算中部地区普通高中教育经费支出效率大小，以便可以提出针对性更强的解决措施，这对优化我国相对不足的教育资源配置效率、教育财政支出效率都具有重要意义。

一、文献综述

纵观国内外研究文献，学者们采用了各种类型的方法来研究教育效率问题。这其中有利用参数法来研究教育效率的，比如Barrow在1991年利用前沿生产函数法对英国20世纪中期中学学校效率进行了研究。［1］Cooper和Cohn在1997年利用前沿生产函数法对南卡罗来纳州中小学学校效率进行了研究。［2］也有学者利用非参数法来计算教育效率的，其中DEA方法就是典型的非参数法。DEA是利用运筹学中线性规划理论估计生产前沿面，然后相对于这个前沿面来计算各种效率。DEA无需预设函数，无需设计权重，并且可以同时对多投入与多产出的领域进行研究，而教育领域就是典型的多投入与多产出的领域。国内外在这方面的研究有很多：Bessent以美国加州某城市学区小学为样本，以学生1976年的阅读和数学成绩、家庭社会经济背景、生均教育经费等作为投入指标，以1977年学生的年阅读和数学测试成绩作为产出指标，从而建立DEA模型进行研究。［3］Ludwin和Guthrie同样也是利用DEA方法建立模型来研究，他们选择学生的能力、阅读、数学和语言测试成绩这4项作为产出指标，选择学生智力水平排名等作为投入指标。［4］

国内有关研究，有梁文艳、杜育红对西部农村小学效率的研究，他们利用DEA数据包络分析法对西部农村小学进行了效率研究，同时还建立了To bit回归模型，分析了农村小学办学效率的影响因素。［5］（P22～34）胡敏、卢振家在《基于DEA模型的教育财政支出效率研究——以广东省为例》一文中，构建了教育财政支出效率的DEA分析模型，选择各级教育毛入学率为输出指标，以生均预算内教育事业费支出为输入指标，分析了广东省2000—2007年教育财政支出效率，发现广东省教育财政支出效率总体不高。［6］（P9～13）也有学者利用数据包络分析法研究了江苏省学前教育财政投入效率，他们选择了江苏省51个县作为样本，研究发现所有样本在学校教育财政投入效率有效方面的占比很低，其中技术效率有效的只有4%，纯技术效率有效的为28%。［7］（P4～8）李玲等人对我国农村义务教育经费配置效率进行了研究，他们的研究是基于DEA和Malmquist指数法，研究我国东中西三个地区以及全国的农村义务教育经费配置效率，研究发现东部地区农村义务教育经费配置效率要低于中西部地区。［8］（P3～7）余游利用数据包络分析不变规模报酬CCR模型、可变规模报酬BCC模型和非增规模报酬FG模型，对云南省2003—2008年城乡义务教育经费投入产出进行了研究，发现云南省城乡义务教育支出有较大差异，并且农村义务教育经费支出效率较低。［9］（P167～170）

综上所述，针对教育经费使用效率的研究主要集中在基础教育经费使用效率，同时研究某个省份的或者全国的教育经费使用效率也比较多，但是针对我国普通高中教育经费使用效率的研究，尤其是针对某个地区的教育经费使用效率研究还比较少。我国中部地区省份都是人口大省，如何优化教育财政资源的配置和使用日趋重要，因此探讨中部地区普通高中教育经费的使用效率具有重要意义。

二、研究方法、数据来源与指标选取

1.数据包络分析法

我们选择DEA数据包络分析法，DEA数据包络分析是由著名运筹学家A.Charnes和 W.W.Cooper以及Rhodes正式提出来，1978年他们在权威的欧洲运筹学杂志上刊登了一篇文章《Measuring the Efficiency of Decision Making Units》，由此开拓了运筹学的一个新领域。DEA主要用来评价相同类型部门中的各个成员间的相对有效性，这也就是被三位作者称为的决策单元，即DMU（Decision Making Unit）。使用DEA进行各决策单元DMUj（j＝1，2，3，……n）之间相对有效性的评价时，首先要根据实际情况和要求确定指标体系，这个指标分为输入指标和输出指标。

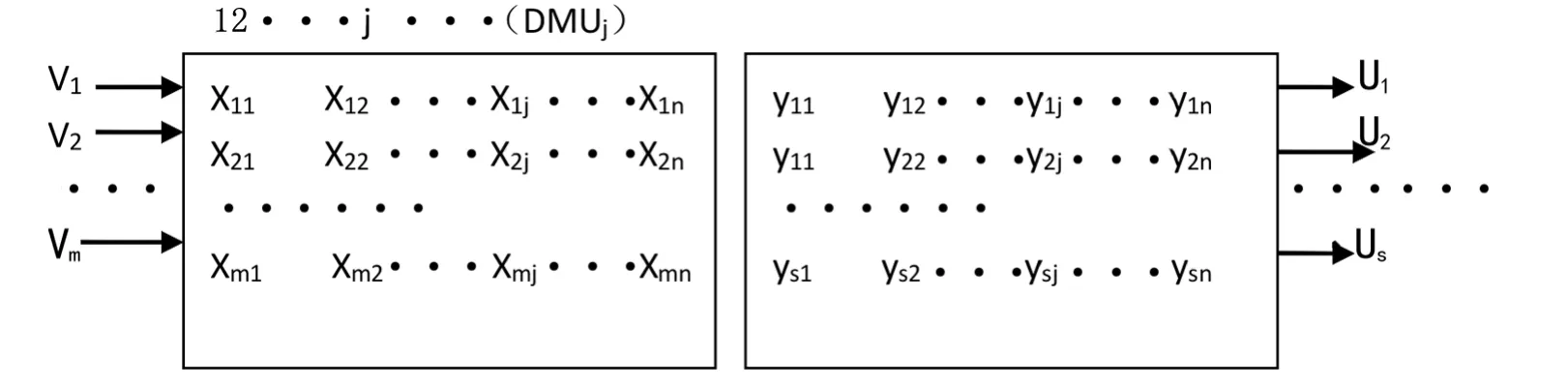
图1 DEA指标体系

Xij代表决策单元j第i项的投入数量，yrj代表决策单元j第r项产出的数量，Vm表示第m决策单元的一种度量权重，Us代表第s决策单元产出的一种度量权重。其中Xij＞0，yrj＞0，i＝1，2，……m；j＝1，2，……n，r＝1，2，……s。DEA在处理多输入与多输出的有效性方面具有很大优势，即使各指标数据的量纲不同，这也不会影响DEA的计算。DEA经典模型有CCR模型和BCC模型。CCR模型是假设规模报酬不变，最终计算出技术效率值，而BCC模型是假设规模报酬可变，最后计算出纯技术效率值，而规模效率值＝技术效率值/纯技术效率值。另外，在DEA模型中的计算还存在投入角度和输出角度，投入角度是指在产出一定的时候，以最小化投入来估计效率，而产出角度是在投入一定时，以最大化产出来估计效率。因为，我们知道普通高中教育经费的来源比较固定，所以应该考虑如何最大化产出，因而本研究中我们选择规模报酬可变下的产出模型。

设有n项的决策单元，每个决策单元都有m种不同输入和s种不同的输出。xij表示决策单元j第i种投入，ykj表示决策单元j第k种产出。决策单元j的投入和产出向量分别为Xj＝ （x1jx2j……xmj）T＞0，Yj＝ （y1jy2j……ysj）T＞0，其中j＝1，2，……n。利用输出角度的可变规模报酬模型评价决策单元的技术有效性时，只是在评价的视角上，当投入为x0时，希望产出由原来y0增大为zy0，也即：

可以写成如下线性规划模型：

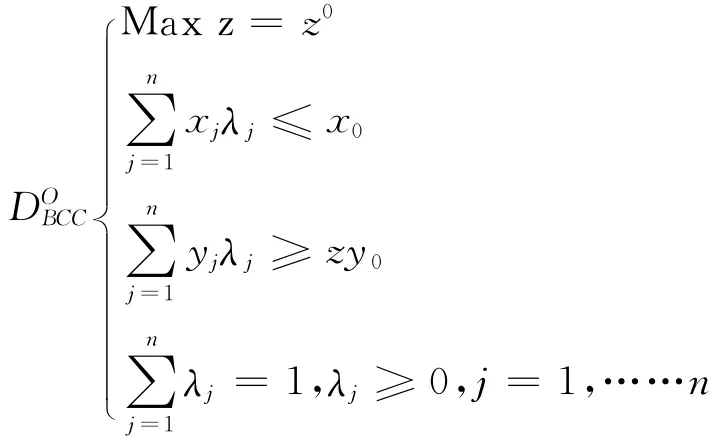
对每一个决策单元，根据上述BCC线性规划模型，都可得出最优解θ·λj·s＊－·s＊＋，DMU效率的有效性判定如下：如果θ＝1，且s＊－＝0，s＊＋＝0时，表示第j决策单元是DEA有效的，但这只是说明该决策单元在这些决策单元中相对有效，并不代表其没有改进的余地。只是相对其他决策单元来说，这个决策单元没有投入冗余造成的资源浪费，也没有产出不足而导致资源分配上的效率损失，只是其相对效率最优，资源配置最好。如果θ＝1，s＊－≠0，或者s＊＋≠0，表示第j决策单元为弱DEA有效，说明其存在着改进的空间。而当θ＜1时，表示第j决策单元为非DEA有效，表明其资源配置未达到最优。

2.二次相对效率法

我们用2010年纯技术效率得分代表基期效率，用2011年纯技术效率得分代表当期效率。然后以2010年纯技术效率得分为投入指标，以2011年纯技术效率得分为输出指标，采用规模收益可变模型得出的效率值，可以称之为管理效率得分。因为这是从一个动态的角度来测量的，其本质上也就是反映经费使用效率有无改善。

3.数据来源与指标选取

本研究所选的数据是最新教育统计年鉴和教育经费统计年鉴中的数据，由于这两个统计年鉴最新出版的是2012年，所以我们采用截止到2012年的年鉴数据。其中各地区普通高中经费收入数据来自于2011—2012年《中国教育经费统计年鉴》，其他数据是来自2010—2011年《中国教育统计年鉴》以及教育部与国家统计局网站上的数据。我们选取了中部地区普通高中教育经费收入作为投入指标；选取学校数、在校学生数、专任教师数以及普通高中师生比为产出指标。对于师生比产出指标而言，由于在年鉴中我们查到的是生师比数据，但是生师比是一个逆指标，所以我们取其倒数。本研究选取的数据是从2005—2011年所组成的面板数据，考虑到文章篇幅与原始数据的繁杂，所以未在文章中列出原始数据。

三、普通高中教育经费支出效率实证分析

使用DEA方法进行效率评价所得到的结果，与投入和产出指标的量纲没有关系，尽管原始数据中有大到百万级别的数，也有小到低于0.1的数，但我们也不必对其进行无量纲处理。根据表中的原始数据我们借助DEAP－xp1软件，运用产出导向型DEA，计算了中部地区8个决策单元2005－2011年的效率得分、纯技术效率得分以及规模效率得分。最后利用二次相对效率法对最近两年（2010－2011年）的普通高中教育经费的管理效率进行了计算。

1.规模收益不变假设下的技术效率得分

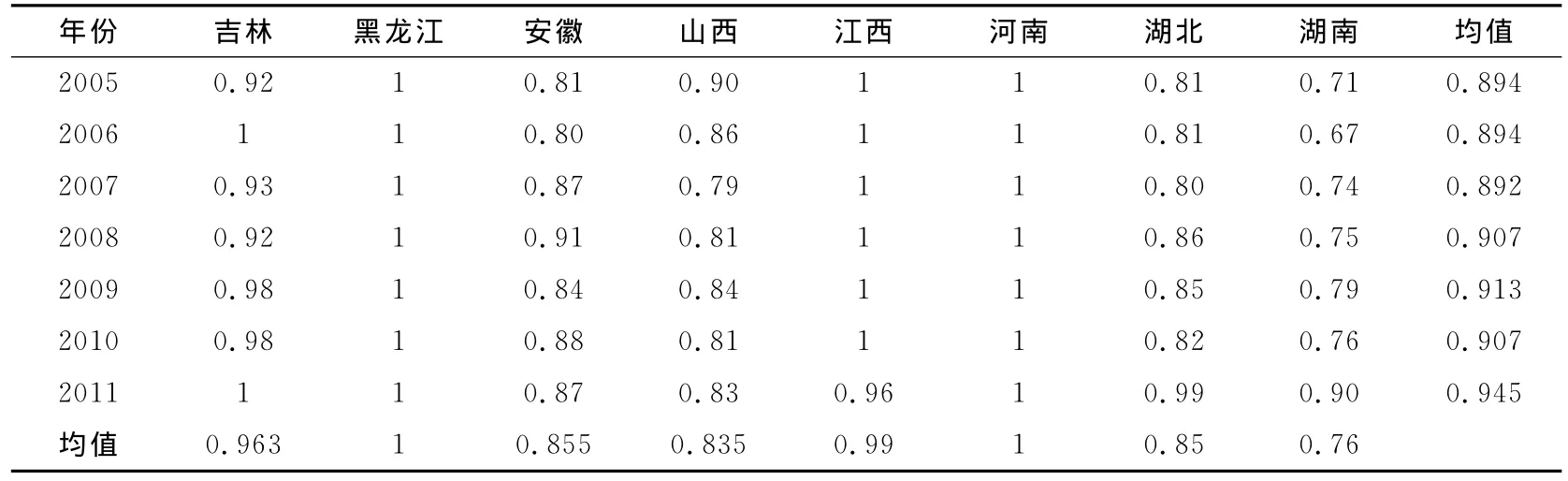
表1 2005—2011年中部地区规模收益不变下的技术效率分值

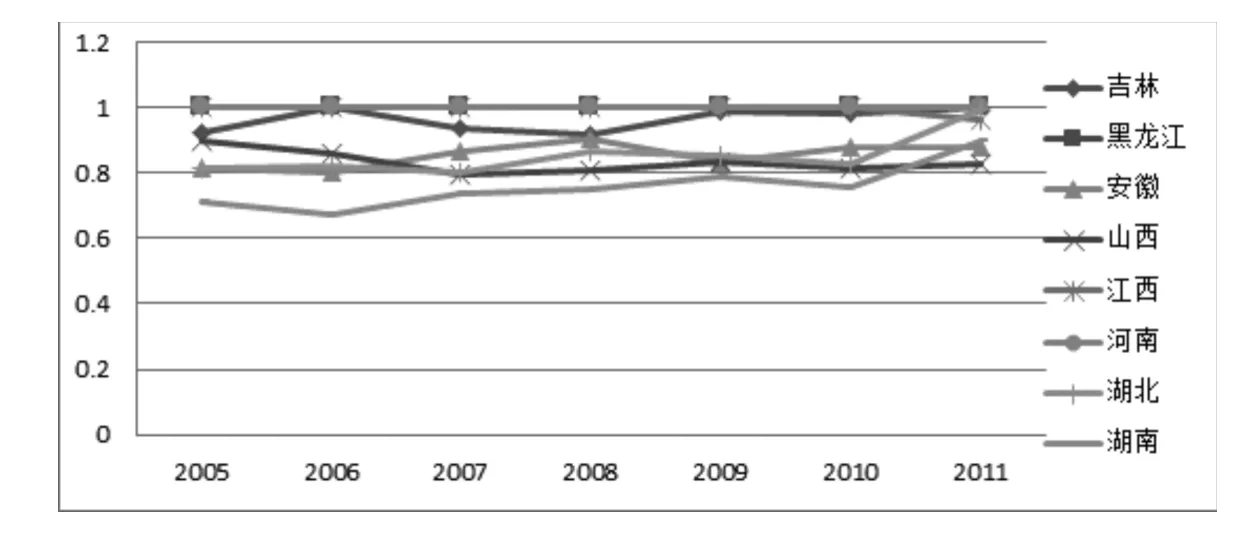
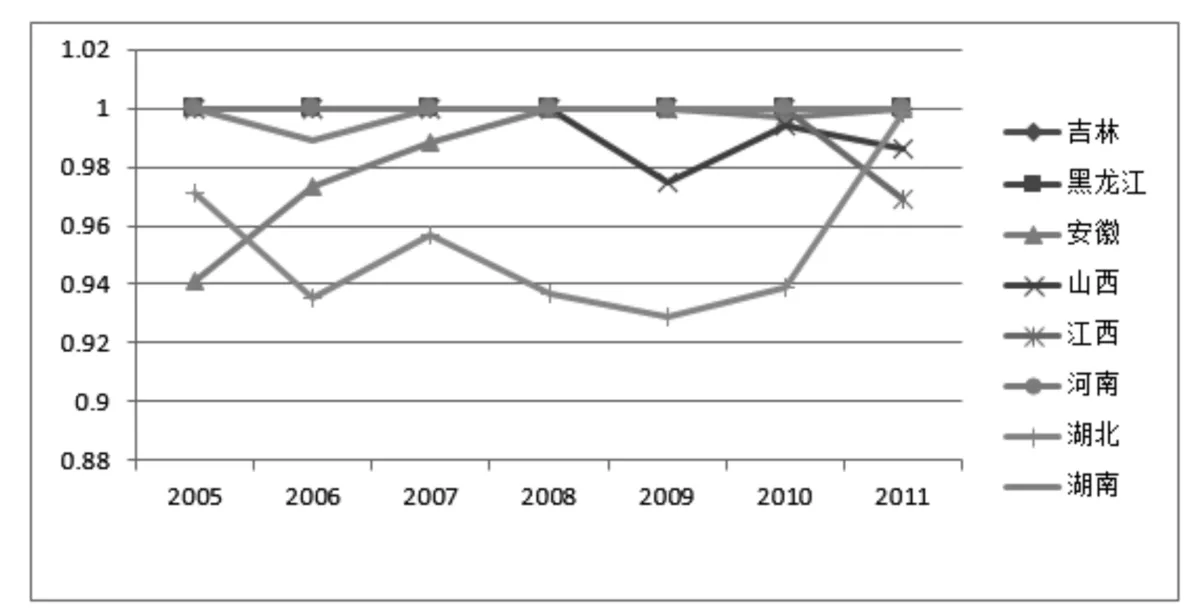
图2 2005—2011年中部地区技术效率得分

各地区技术效率得分计算结果于表1和图2中所示。从结果可以看出，2005—2011年中部地区整体技术效率得分均值呈现递增趋势，分别为0.894、0.894、0.892、0.907、0.913、0.907、0.945。而且每年也都有技术效率达到最优的省份。其中黑龙江省与河南省连续7年来都是技术效率得分为1。吉林省在2006年和2011年技术效率达到最优，而江西省从2005—2010年一直都是技术效率得分为1，但是在2011年技术效率却出现了下降，技术效率得分为0.96。而对于安徽、湖北和湖南三省来说，总体上这三个省份的技术效率得分呈上涨趋势，尤其对湖北省和湖南省来说2011年的技术效率得分都达到0.9，特别是湖北省的效率得分已经为0.99，这说明近年来湖北与湖南两省在经费支出效率上减少了资源浪费并且增加了产出。另外，从各地区平均技术效率得分的横向角度来比较，可以看出黑龙江省与河南省均值为1，紧随其后的是江西省，均值为0.99。平均技术效率得分最低的是湖南省，均值为0.76，最高与最低效率得分相差为0.24。

2.规模收益可变假设下的纯技术效率得分

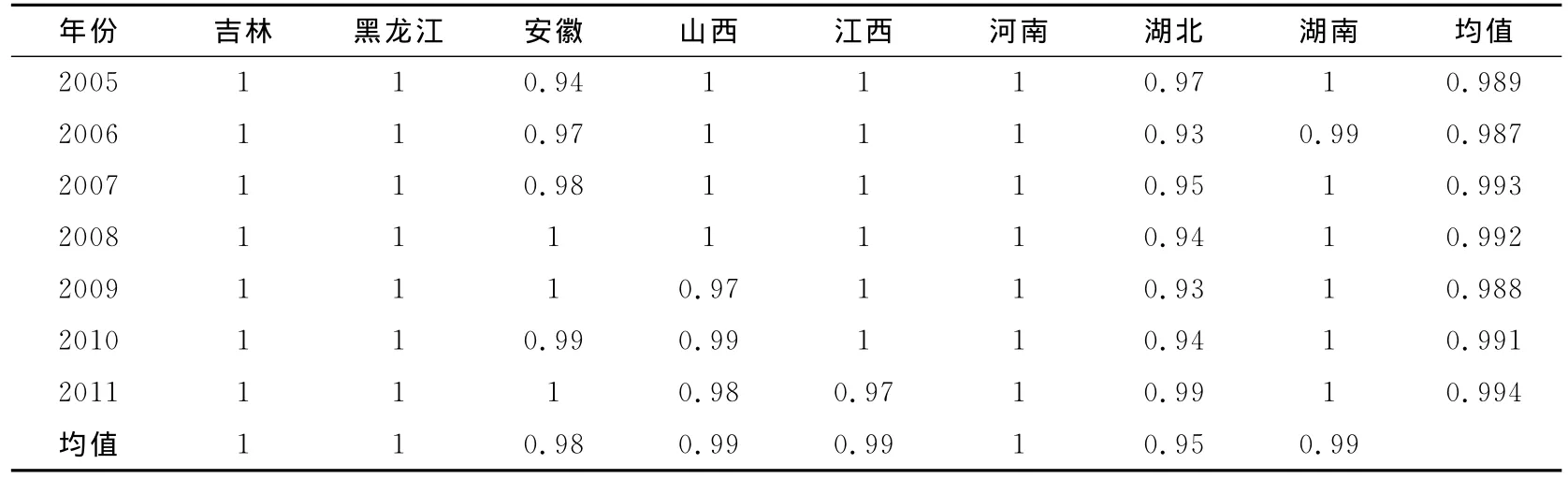
表2 2005—2011年中部地区规模收益可变下的纯技术效率分值

规模收益可变下的纯技术效率计算结果见表2所示。可以看出从2005—2011年，中部地区整体上纯技术效率值基本保持稳定，分别为0.989、0.987、0.993、0.992、0.988、0.991、0.994。从规模收益可变下的纯技术效率得分来看，每年达到纯技术效率有效的省份，要远多过于规模收益不变下的技术效率得分的省份。而且从2005－2011年以来，各省份的平均纯技术效率得分都在0.95以上，并且得分相差也不大。这表明中部地区普通高中教育经费的投入（普通高中教育经费收入）相对于其产出（在校学生数、专任教师数等）而言是很适当的，既没有投入冗余也没有产出不足现象。从上述结果可以看到，在规模收益不变的假设下，达到有效的省份是黑龙江与河南；而在规模收益可变假设下，纯技术效率得分为1的是吉林、黑龙江与河南三省。

3.规模效率得分

按照DEA模型，规模效率得分等于技术效率得分与纯技术效率得分之比，由此可以计算2005—2011年中部地区各省份的规模效率值，并且可以判断各个省份是处于规模报酬递增阶段、规模报酬递减阶段还是规模报酬不变阶段。由表3结果显示，在2005—2011年期间，黑龙江省与河南省一直处于规模报酬不变阶段，而吉林省从2005—2010年间一直处于规模报酬递增阶段，而2011年处于规模报酬不变阶段。而安徽、山西、湖北与湖南四省一直处于规模报酬递减阶段，这说明大部份省份的效率上升空间已经不大，所以国家在经费投入不减少的情况下，应该要督促这些地区尽量增加产出，同时避免浪费。

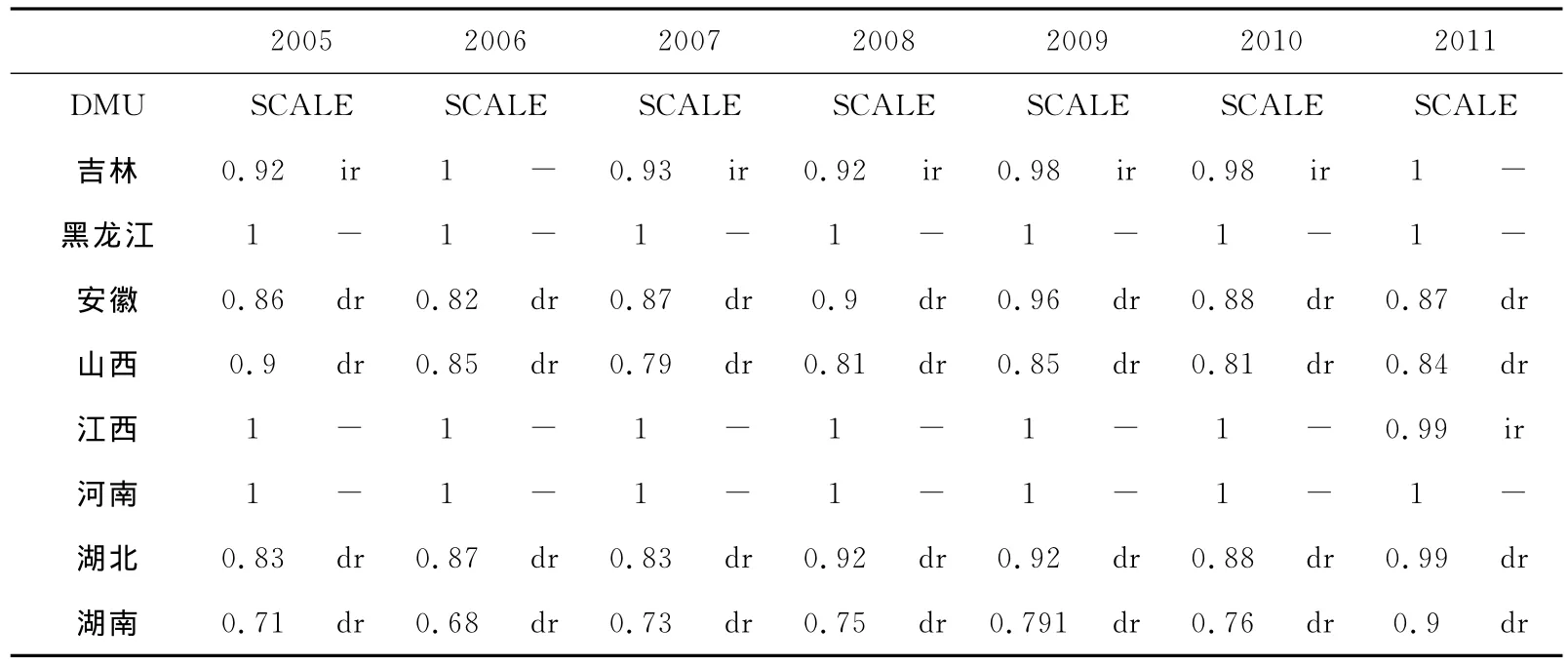
表3 2005—2011年中部地区规模收益可变下的规模效率分值

4.二次相对效率分析结果

再以2010年纯技术效率得分为投入指标，以2011年纯技术效率得分为输出指标，采用规模报酬可变模型计算出管理效率得分。其投入与输出指标数据如表4所示：

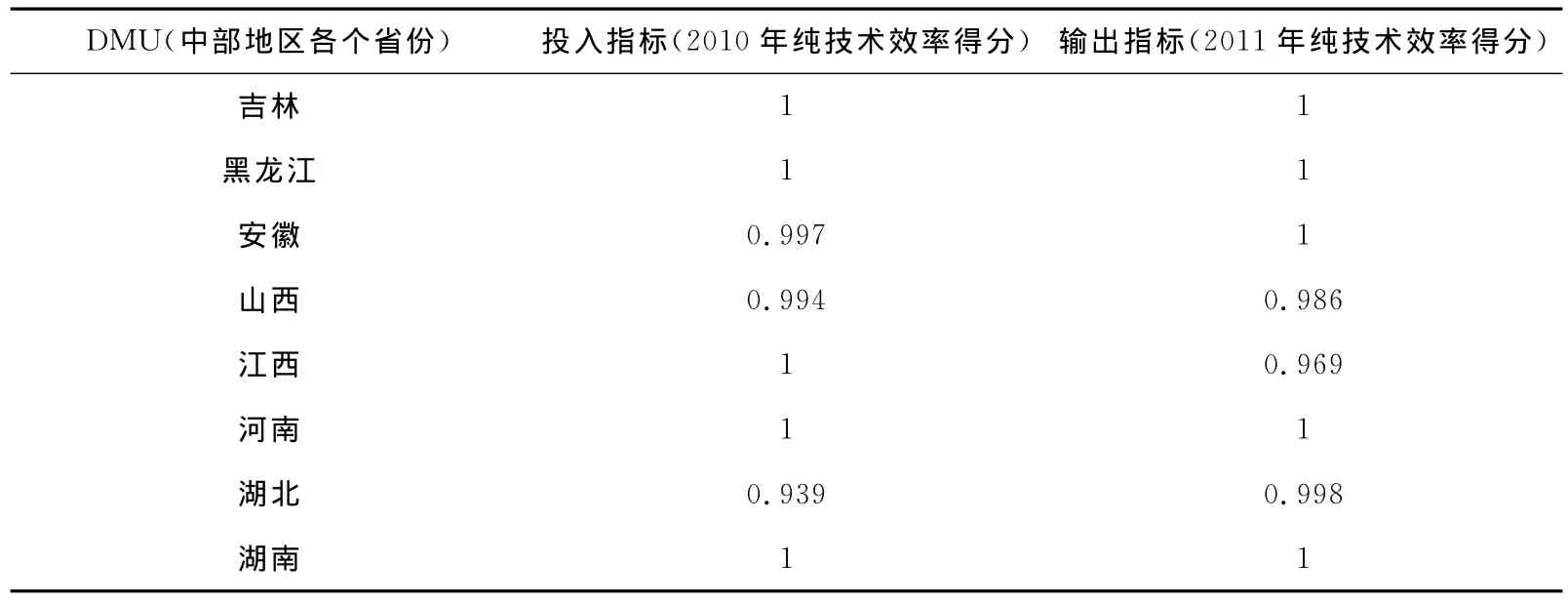
表4 二次相对效率法的投入与产出指标

基于基期效率和当期效率得分结果，我们从动态角度计算出中部地区省份普通高中教育经费支出的管理效率得分，也就是各省普通高中教育经费使用的改善情况。再者，我们从静态的角度将基期效率与当期效率得分求平均值，以此来评价教育经费的配置效率。其结果如表5和图4所示：

表5 决策单元管理效率和配置效率得分

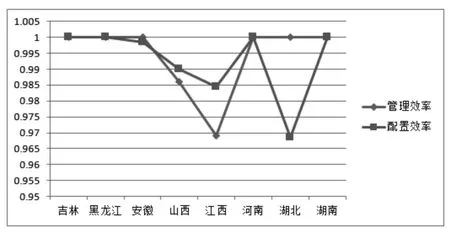
上述结果表明，中部地区省份在管理效率得分上相差不大，并且有6个省份管理效率都达到1，说明其资金使用有所改善。在这8个省份中，只有山西省和江西省的管理效率得分小于配置效率得分，说明这两个省份忽视了自身改善教育经费的使用效率，证明其普通高中教育经费支出效率存在着较大的改善空间。

四、结论与政策建议

通过此次研究，我们发现从整体上来说，中部地区从2005年到2011年普通高中教育经费支出效率得分呈上升趋势。但是在中部8个省份之间普通高中教育经费的使用效率也存在着差距，如安徽、山西、湖南和湖北四省连续7年都是非DEA有效。

我们从2011年三个效率得分结果来看，只有吉林、黑龙江以及河南三省技术效率值、纯技术效率值和规模效率值得分都为1。而其余5个省份中，像安徽和湖南两个省份，尽管他们的纯技术效率得分都为1，但规模效率不高。由于技术效率＝纯技术效率×规模效率，所以安徽省与湖南省的普通高中教育经费未达到有效，是源于其规模的无效。并且从规模报酬结果来看，他们都属于规模报酬递减阶段，这也就表明安徽省和湖南省效率得分无效，源自经费投入过多但却没能有效利用。

江西省应该继续增大投入力度，因为江西省仍然处于规模报酬递增阶段，其技术效率得分和纯技术效率得分虽然没有达到1，但是已经非常接近DEA有效了。应该要继续增加经费投入，从而扩大学校规模。而对于处在规模报酬递减阶段，并且效率得分小于1的山西与湖北两个省份来说，应当要适当减少教育资源的投入。近年来，随着普通高中教育经费的不断加大，各级政府更应当注意经费使用效率问题，要督促各地区学校努力改善学校教学质量，调整学校的布局，从结构上优化普通高中教育资源的配置，同时，还应当从外部加强对普通高中教育经费使用的监督，加大普通高中教育财政资金的审计工作，努力减少普通高中教育经费乱用浪费的现象，从而才能保证经费的有效合理利用。

［1］ Barrow.Measuring Local Education Authority Performance：A Frontier Approach［J］.Economics of Education Review，1991.

［2］ Cooper S.T.，COHN.Estimation of a Frontier Production Function for the South Carolina Educational Process［J］.Economic of Education Review，1997.

［3］ Bessent A.，Bessent.Determining the Comparative Efficiency of Schools through Data Envelopment Analysis［J］.Educational Administration Quarterly，1980.

［4］ Ludwin W.G.，Guthrie T.L.Assessing Productivity with Data Envelopment Analysis［J］.Public Productivity Review，1989.

［5］ 梁文艳，杜育红.基于DEA－Tobit模型的中国西部农村小学效率研究［J］.北京大学教育评论，2009，（4）.

［6］ 胡敏，卢振家.基于DEA模型得教育财政支出效率研究——以广东省为例［J］.肇庆学院学报，2010，（1）.

［7］ 王水娟，柏檀.学前教育财政投入的效率问题与政府责任［J］.教育与经济，2012，（3）.

［8］ 李玲，阎德明，黄宸.我国农村义务教育经费配置效率研究——基于DEA和 Malmquist指数的实证分析［J］.教育与经济，2014，（3）.

［9］ 余游.云南省义务教育经费支出效率的城乡差异分析［J］.学术探索，2012，（3）.