双生命状态下住房反抵押贷款定价研究

■ 周海珍，金逸娟，陈秉正

一、引言

我国已经进入老龄化社会。至2014年末我国60岁及以上人口为2.12亿，占总人口的15.5%，其中65岁及以上人口为1.38亿，占总人口的10.1%①国家统计局.2014年国民经济在新常态下平稳运行[EB/OL].http://www.stats.gov.cn/tjsj/zxfb/201501/t20150120_671037.htm l.。随着老龄人口的快速增加以及我国家庭呈现的“4-2-1”结构和整个国家“未富先老”等特点，老年人的经济保障问题日益引起各界的广泛重视。作为可以提高老年人经济保障水平的一种财务安排，住房反抵押贷款已经引起了社会的广泛关注。2013年9月，国务院在 《关于加快发展养老服务业的若干意见》（国发（2013）35号）中明确提出要“鼓励探索开展老年人住房反向抵押养老保险试点”，并决定从2014年开始在北京、上海等城市试点。

近年来，国内外学界已经对住房反抵押贷款的相关问题进行广泛深入的研究，其中定价问题是最主要的内容之一。最早给出反抵押贷款定价模型的是Szymanoski（1994），该文章用随机游走过程描述了房屋价值的波动；Peter Chinloy等（1994）设计的支付因子定价模型极具代表性，在综合考虑了贷款利率、通货膨胀率、房产波动率和调整精算系数等因素后计算出了支付因子，用该因子乘以住房价值即可得到借款人能够获得的贷款额度；Olivia S.Mitchell等（2004）则提出了保险精算定价模型，根据这个模型，在已知一定的贷款利率、房价增长率和借款人生存率的前提下，可计算出借款人的趸领金额和按期领取的年金金额；Bardhan，Karapanda和Urosevic（2006）构建了BKU模型，该模型是在风险中性的前提条件下，利用欧式看跌期权对住房反向抵押贷款进行了定价；Seungryul Ma等（2007）则在BKU模型的基础上，根据保费收入现值与预期损失现值平衡的原则，构建了住房反向抵押贷款定价模型。

国内学者也对住房反抵押进行了很多研究，但较多集中在对必要性、可行性及运行模式等方面的研究，对定价问题则研究得较少。刘春杰和谭竞（2005）以支付因子定价方法为基础探讨了反抵押贷款合约的定价问题；奚俊芳（2007）介绍了终身年金给付模式下单生命体和双生命体的定价方法，并构建了不同递增方式的年金给付定价模型；范子文（2006)和柴效武（2008）研究了基于无赎回权的年金产品定价模型；同时，范子文（2006)首次在国内提出了有赎回权的反向抵押贷款定价模型，并利用BS模型的定价方法对赎回权进行了分析；此外，陈秉正（2014）等构建了包含随机动态房价和随机动态利率的具有赎回选择权的住房反抵押贷款定价模型，并将住房反抵押贷款和长期护理保险相结合，建立了具有长期护理保障功能的住房反抵押产品定价模型。

根据对国内外住房反抵押贷款定价研究的综合分析我们发现，现有的研究基本上是假定借款人为一个老年人，而现实中很多老年家庭是夫妇二人共同生活，共同拥有一套房屋。因此，以家庭作为借款单位会更适合现实情况，这就需要研究双生命状态下的住房反向抵押贷款定价模型。基于这一考虑，本文研究了双生命状态下住房反抵押贷款定价问题，建立了相关定价模型，并进行了价格测算。我们的研究结果表明，和以往的单生命状态假设下的定价模型相比，根据双生命状态假设得到的定价结果可以为老年人提供更高程度的经济保障。

二、双生命状态下住房反抵押贷款的定价模型

（一）单生命状态下的反抵押贷款定价模型

为简单起见，我们假设反抵押贷款市场是一个完全竞争的市场。对于贷款人来说，被抵押房屋的终期价值是其可获得的收入，在期初向借款人发放的贷款额是其所支付的成本。根据无超额收益原则，两者的精算现值应该相等。

记tPx为x岁的人于第t年后仍然生存的概率，亡的概率，H （t）为所抵押的房屋在第t年的价值，r为贷款利率，是无风险利率与风险升水成本和一定利润率之和，a为发起费，β为保险费，γ为其他交易费用，如第三方服务费、手续费等。若借款人在第T年死亡，贷款人将房屋价值变现所得收入的精算现值为：

根据贷款人期望收支相等的原则，式（1）的值即为借款人可得到的贷款总额LSx：

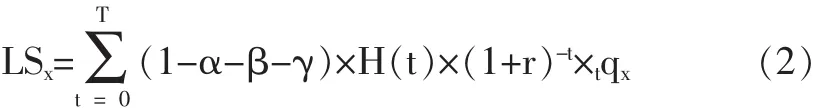
假设贷款机构在每年年初给付借款人一笔等额的贷款额，直至借款人死亡当年即第T年为止。若以Ax表示年龄为x岁的借款人每年年初可获得的贷款金额，则根据该借款人在整个生存期内获得的贷款的期初现值应该等于其可以得到的总贷款金额这一原则，可以得出：

（二）双生命状态下的反抵押贷款定价模型

在现实生活中，很多老年家庭都是夫妇双方一起生活的，在反抵押贷款合同签订后，假如一位老人去世，另一位老人仍然健在的话，此时贷款机构强行将住房收回是很不合情理的。因此，我们假设可以家庭为申请贷款的单位，当夫妻双方均死亡后贷款机构才将房屋收回，据此可以建立双生命状态下的住房反抵押贷款定价模型。根据两个老人中有一个去世后贷款是否继续发放，可以将双生命状态下的反抵押贷款细分为联合生存发放方式和最后生存者发放方式，我们下面分别对这两种方式的定价模型进行阐述。

1.联合生存（xy）发放方式下的定价模型

在此状态下，房屋进行反抵押后，如果两位老人中一方去世，贷款机构将停止给付年金，但房屋一直保留到另一方去世后再收回。这种情况适用于有收入但收入不足以承担两个人生活的家庭。

我们用Axy表示申请住房反抵押的家庭每年所能领取的贷款金额，其中x表示申请时男方的年龄，y表示申请时女方的年龄，根据期望收支平衡原则，申请反抵押贷款的家庭可获得的贷款总额LSxy或分配到各年所能领取的贷款金额Axy分别为：

其中tqxy为初始年龄为x和y的借款组合在第t年内有一人死亡的概率，tpxy表示初始年龄为x和y的借款组合在年内存活的概率。

2.最后生存者（xy）发放方式下的定价模型

在此状态下，房屋进行反抵押后，假如两人都生存，则每年可以获得的贷款金额为Axy，如果其中一方去世另一方健在的话，贷款将继续发放但金额有所降低，直至另一方去世后贷款机构再将房屋收回，这种设计特别适用于无其他经济来源的家庭。

同样，用x表示申请时男方的年龄，y表示申请时女方的年龄，最后生存者状态下借款者可获得的贷款LSxy与联合生存者状态下是一样的，如式（6）所示：

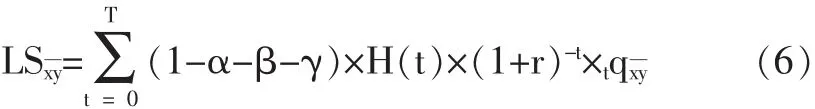
假定一方去世后，贷款发放数额为原先的1/2，则该状态下每年贷款的发放方式相当于联合生存发放方式和最后生存者发放方式的组合，即由50%的最后生存者状态下发放的贷款加上50%的联合生存者状态下发放的贷款，即：

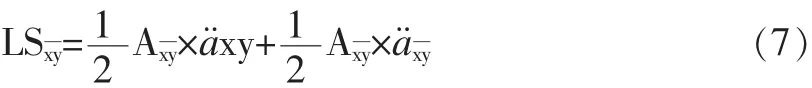
将式（4）代入式（7）可得：

其中tpxy表示初始年龄为x和y的借款组合在t年内至少有一人存活的概率。

由式（8）可以得出最后生存者状态下每年贷款的发放额：

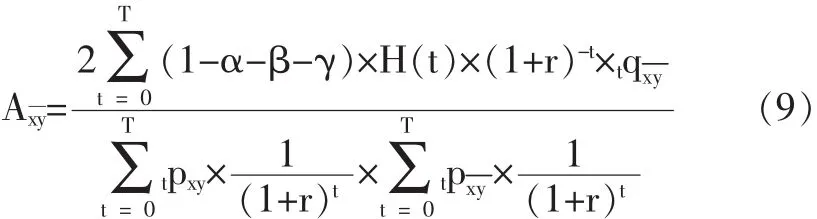
三、双生命状态下住房反抵押贷款定价的模拟分析

我们假设借款人在生日当天签订反抵押产品合约；借贷双方此后均不存在违约行为；借款人选择于期初一次性获得贷款或每年获得一定数额的贷款金额；借款人或借款人夫妇去世后，房屋产权转移给贷款人用以清偿贷款，不存在赎回选择权，且贷款人拿到房屋所有权后即以市场价出售，两者间不存在时间差。

（一）参数假设与选择

1.房产价格及发展趋势。假设借款人所拥有的房屋的初始评估价值H （0）为100万，根据中国1998～2014年的商品房平均销售价格，我们计算得出过去17年间房价平均年增长率为7.20%，其中2004年、2005年以及2007年房价增长率均超过了14%，2009年甚至超过了23%。一般认为，房价波动与国家政策、GDP以及人均收入增长幅度等因素相关。随着国家对房价调控力度的加大，未来房价的增长不太可能会维持在如此高位，因而在考虑国家调控政策、GDP以及人均收入增长速度的基础上，我们假设未来中国长期房价平均的增长率为6.50%；同时按照住房70年的使用年限并采用直线法折旧，并考虑到房屋拥有者将房屋办理反抵押后可能会疏于维修保养等道德风险因素，将年折旧率定为2%。因此，最终设定房价年均增长率的均值为6.5%-2%=4.5%。

2.贷款利率。本模型中的利率由无风险利率、风险报酬率和贷款机构合理的利润率三部分构成。我们假设无风险利率为一固定值，以2015年1月某日上海银行间同业拆放7天利率3.88%作为无风险利率，风险报酬率为2%①因为我国目前尚未开始实施住房反抵押贷款，只能参照现有文献研究结果确定风险报酬率（范子文，2011）。；同时根据银监会发布的数据，2013年我国商业银行的平均资产利润率为1.345%②中国银监会.2013年商业银行主要监管指标情况表.[EB/OL].http://www.cbrc.gov.cn/chinese/home/docView/123C72BD103540C2B679F0A4BA19E903.htm l.2014-02-13.。由于考虑到住房反向抵押贷款的期限较长，风险较大，本文将贷款机构的利润率取为1.5%。因此，贷款利率r=rf+2%+1.5%=7.38%。

3.其他参数，包括发起费、保费和其他交易费用。目前我国还没有正式实施住房反向抵押贷款业务，所以本文参照美国的运作标准确定一些交易费用。其中发起费全部由申请人支付，为房屋初始价值的1%；保险费为房屋初始价值的2%；其他交易费用如第三方服务费、手续费等，假设为房屋初始价值的 3%③因为我国目前尚未开始实施住房反抵押贷款，只能参照现有文献研究结果确定其他参数（范子文，2011）。。

4.死亡率。本文的死亡率数据源自《中国人寿保险业经验生命表（2000～2003）》。假设借款夫妇二人的预期寿命相互独立，且在各年度内的死亡服从均匀分布（UDD），根据生存率与死亡率之间的关系，可分别计算式（4）至式（9）中各生存率和死亡率的数值①由于篇幅关系，计算结果不在文中一一列出。。

5.从借款人签订合约到死亡的年数T。我们以生命表中的终极寿命105岁为借款人的预期寿命，即如果借款人在60岁时将房屋进行反抵押，则T=45；如果在70岁时办理房屋抵押，则T=35，依此类推。

（二）数值模拟结果分析

1.单生命状态下借款人所能获得的贷款金额

根据上文的假设，我们能得出一男性在60岁、65岁、70岁、75岁时申请住房反抵押贷款所能从贷款机构获得的趸领金额 （保险合同中保险金领取方式的一种，即保险合同到期后一次领取全部保险金）或年领金额的数值如表1所示。

表1 不同年龄男性借款人可获得的贷款金额（房屋初始价格为100万元）单位：元

从表1可以看出，借款人可获得的贷款金额与申请人的年龄成正比关系，随着借款人年龄的增加，所获得的贷款金额也随之增加，这是因为年龄越大，预期余寿越短，贷款可能归还的期限也越短，从而所获得的贷款金额也就越大。

2.双生命状态下借款人所能获得的贷款金额

（1）联合生存者发放方式

根据上文的假设，我们可以得出当一对夫妇在（60,55）（65,60）（70,65）（75,70）等四种不同年龄组合下②假设年龄组合中第一个数字为男方年龄，第二个为女方年龄。申请反抵押贷款时可从贷款机构获得的贷款金额，如表2所示。

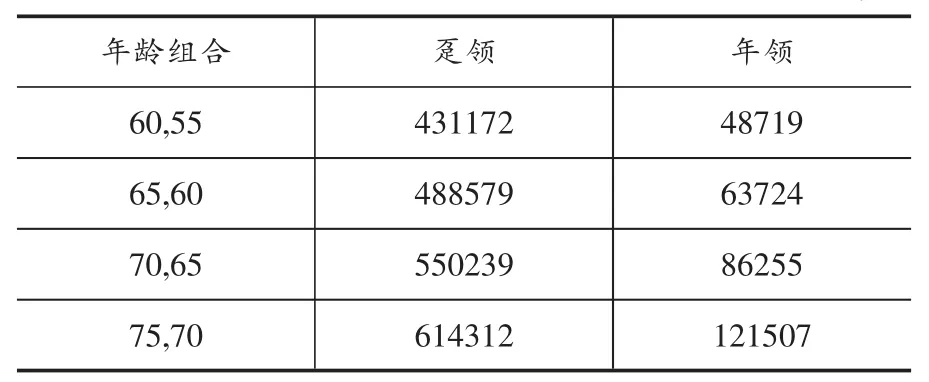
表2 联合生存状态不同年龄组合借款人的贷款金额（房屋初始价格为100万元）单位：元

（2）最后生存者发放方式

如果一对夫妇同样在上述四个年龄组合下申请反抵押贷款，但选择了最后生存者发放方式，一方去世后贷款发放额为原来的1/2，则该夫妇可以获得的贷款金额如表3所示。

表3 最后生存者状态不同年龄组合借款人的贷款金额（房屋初始价格为100万元）单位：元

在双生命状态下，虽然相同年龄组合的借款夫妇选择两种不同发放方式能获得的总贷款金额的期初现值是相同的，但若选择联合生存者发放方式，在夫妇两人均存活时，每年从贷款机构领取的金额比选择最后生存者发放方式获得的贷款要多，且该差额随着申请年龄的增加而增加。当年龄组合为（60，55）时，选择联合生存者发放方式的借款人每年从贷款机构领取的金额比选择最后生存者发放方式获得的贷款要多15.6%，当年龄组合为（65，60）时为21.03%，当年龄组合为（70，65）时为 28.1%%，而当年龄组合为（75，70）时则为37.23%，这主要是因为联合生存者发放方式下，只有当夫妇二人均存活时，贷款机构才继续发放贷款，只要其中一人去世则贷款机构将停止发放贷款；而在最后生存者发放方式下，夫妇二人中只要有人存活，贷款机构就会一直发放贷款，直至最后一人去世，即联合生存的贷款发放期会短于最后生存者的贷款发放期，每期可获得的金额自然要多一点；且随着年龄的增长，贷款发放的年数减少，因而两者的差距会加大。

四、主要影响因素的敏感性分析

从前述住房反向抵押贷款定价模型可以看出，房屋价格、利率等因素会对住房反抵押贷款的经营带来巨大影响。由于我国经济仍处于一个较快发展的阶段，房价和利率等均会受到经济发展和政府政策的较大影响，具有较大的不确定性。因此，有必要对前面的数值模拟结果进行了必要的敏感性分析，以检验房价和利率的变动对贷款金额的影响。

（一）房价波动的敏感性分析

作为住房反向抵押贷款定价的最主要影响因素之一，房价在贷款期内的波动会直接影响房产未来的变现价值，进而会对经营反抵押贷款的机构的经营结果带来显著影响。为了分析未来房价变化对住房反抵押贷款的影响，我们假设房屋的初始价值H（0）为100万，但未来的增长可能出现多种情形，并计算出不同房价增长率情形下借款人应获得的贷款金额，具体数值如表4所示。

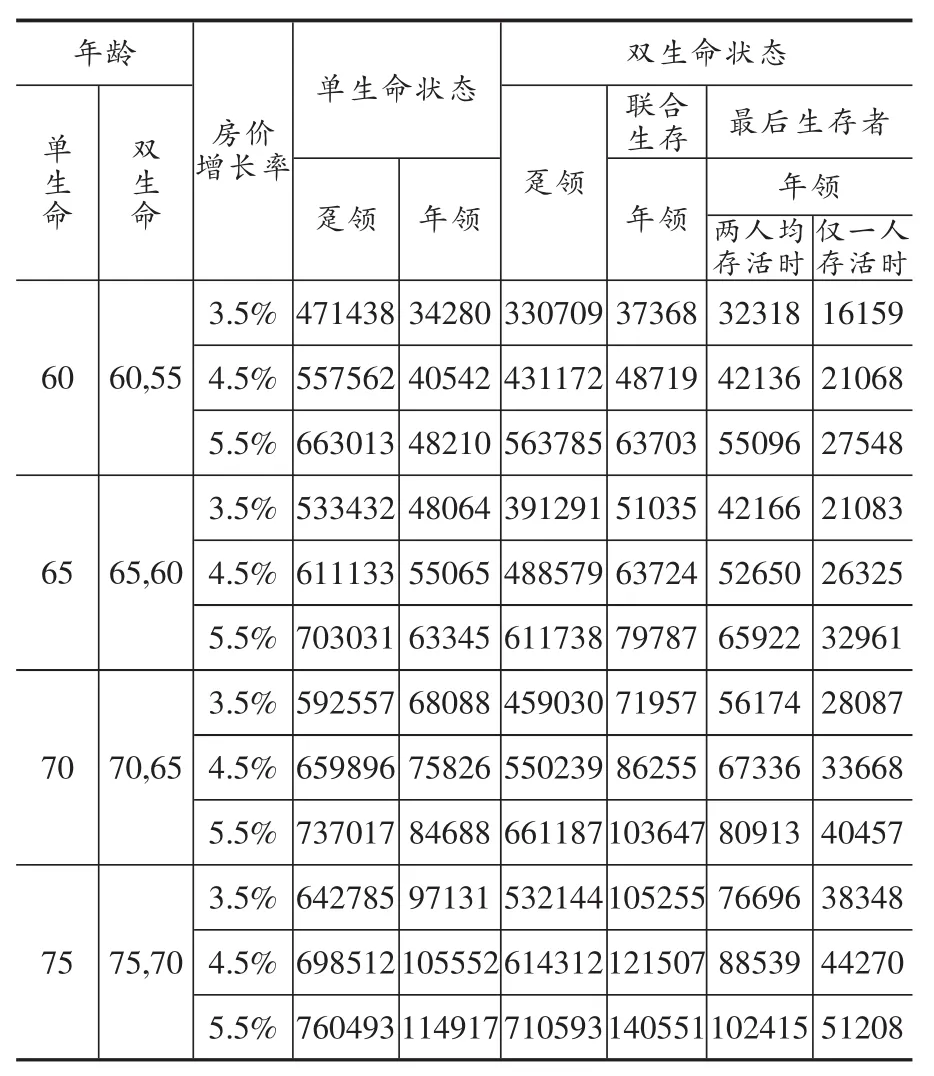
表4 不同房价增长率下借款人的贷款金额（房屋初始价格为100万元）单位：元

从表4可以看出，房价增长率与贷款金额呈同方向变动，房价增长率越高，相应的贷款金额也越高。以单一借款人为例。当借款人年龄为60岁时，当房价增长率由4.5%变为5.5%时，借款人每年可获得的贷款额由40542元增加到48210元，增长了18.9%，敏感度系数为0.85；在同样条件下，当借款人年龄为65岁时，所获得的贷款额由55065元增加到63345元，增长了15%，敏感度系数为0.68。这说明，随着房价的增长，借款人所获得的贷款金额随之增加，但随着借款人年龄的增大，贷款金额对房价增长率变化的敏感性在逐渐降低。这是因为借款人年龄越大，平均余寿越短，因此房价波动的积累效应相对较小，对贷款额的影响也较小。

再以借款人组合（60，55）为例。在其他参数不变的情况下，如果房价增长率假设由4.5%变为5.5%，则双生命状态下的两种贷款发放方式每年可获得贷款金额对房价变化的敏感度系数均为1.38，大于单生命状态下的敏感度系数，说明双生命状态下可获得贷款金额对房价的变动更为敏感。这是因为双生命状态下，贷款机构要等到夫妇二人均去世后才将房屋收回，因而贷款期限是借款组合中寿命较长者的剩余寿命，较单生命状态的贷款期限长，因而受房价波动的影响会更大。

同样在双生命状态下，如果我们将（60，55）借款组合和（65，60）借款组合进行比较会发现，（65，60）借款组合在两种贷款发放方式下年可获得贷款金额对房价变化的敏感度系数均为1.13，略低于（60，55）借款组合下的敏感度系数。这说明借款人年龄越大，其平均余寿越短，因而房价波动所带来的影响也相对较小。

（二）利率波动的敏感性分析

利率假设是影响住房反向抵押贷款定价的另一主要因素。为了分析不同利率假设对住房反向抵押贷款的影响，我们假设房屋的初始价值H（0）为100万，计算了不同利率假设水平下单、双生命状态下不同的贷款金额，具体数值如表5所示。

从表5可以看出，利率与贷款金额呈反方向变动，利率越高，所能获得的贷款金额就越低。具体而言，当借款人年龄为60岁时，当假设利率由7.38%变为8.38%时，每年可以获得的贷款金额由40542元变为35876元，减少了11.51%，敏感度系数为-0.85；而同样的条件下，当借款人年龄变为65岁时，每年可获得的贷款额55065元变为50235元，敏感度系数为-0.65。这说明，随着借款人年龄的增大，利率对贷款金额的影响是逐渐减小的。

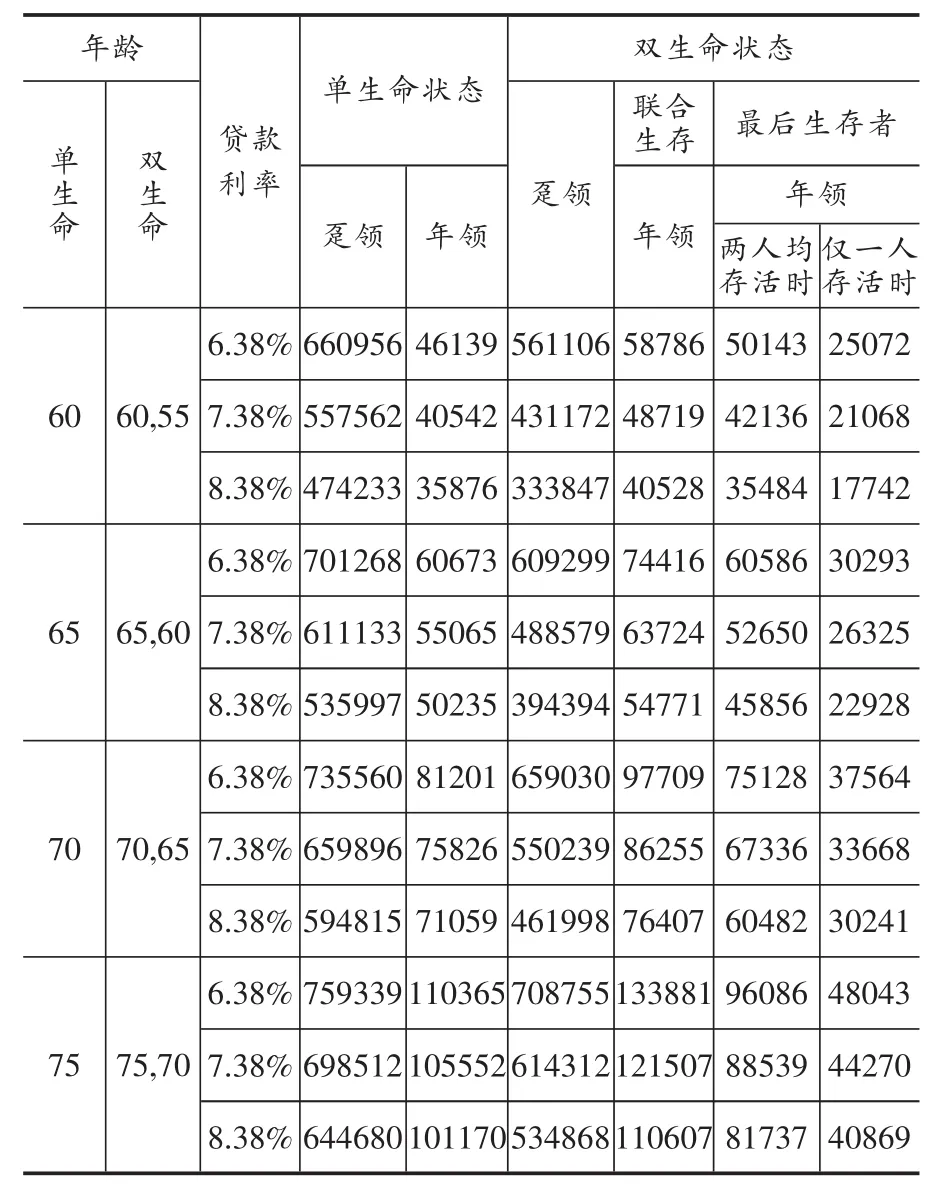
表5 不同贷款利率下借款人的贷款金额（房屋初始价格为100万元）单位：元

再以60岁的单个借款人和（60，55）的借款组合为例，双生命状态下每年可获得贷款额对利率的敏感度系数为-1.24，其绝对值大于单生命状态下的敏感度系数的绝对值，说明相对于单生命状态而言，双生命状态下可获得的贷款金额对利率的变动更加敏感。这是由于双生命状态下的贷款期限是借款组合中寿命较长者的剩余寿命，一般比单生命状态下的贷款期限要长一些，因而受利率变动的影响也就更大。

同样在双生命状态下，以（60，55）的借款组合为例，当假设的利率增加一个百分点即由7.38%增加到8.38%时，在联合生存和最后生存者给付方式下，每年可获贷款额年对利率的敏感度系数为-1.24；而（65，60）借款组合在两种给付方式下可获得贷款额对利率变动的敏感度系数为-1.04，其绝对值略低于（60，55）借款组合下的敏感度系数的绝对值。这是因为借款人年龄越大，平均剩余寿命越短，因此利率波动的积累效应相对较小。

从上述敏感性分析结果还可以看出，不管是单生命状态还是双生命状态，可获得的贷款额都对房价的波动表现得更加敏感，这是因为虽然利率波动对未来房产价值的现值和累积贷款总额的现值都有影响，但其中有部分影响会相互抵消；而房价波动只对未来房产价值产生影响，累积效果较大，所以影响程度也较大。

五、结论与展望

本文建立了双生命状态下反抵押贷款的定价模型，同时利用中国房地产市场、死亡率和利率等数据，计算了住房反抵押贷款的金额。此外，我们还对影响反抵押贷款金额的主要因素如利率和房价等进行了敏感性分析，所得结果有助于金融保险机构在设计住房反抵押产品时了解各类风险因素的影响并进行有效的风险管理。

我们的数值测算结果表明，住房反抵押产品的推出可以使老年人在不丧失房屋使用权的同时，让他们增加一笔可观的经济收入，显著改善退休后的生活水平。这种安排在中国人口老龄化日趋严重、社会保险提供的养老金水平较低的背景下显得尤为重要。

对重要影响因素的敏感性分析的结果表明，反抵押贷款的金额对利率和房产价格的变化十分敏感；但随着借款人申请反抵押贷款时的年龄越大，房价和利率变动对贷款金额的影响越小；而且不管是对于房价变动还是利率变动，双生命状态下贷款金额的变动都表现得比单生命状态下贷款金额的变动更加敏感。

本文的模型和数值模拟分析中所采用的死亡率、房价增长率、利率等均为固定数值，并没有考虑这些因素的随机动态变化，这是未来研究需要进一步拓展的方面。

[1]Szymanoski，E.J.,Risk and Home Equity Conversion Mortgage [J].Journal of American Real Estate and Urban Economics Association,1994(22):347～366.

[2]Peter Chinloy，Isaac F Megbolughe,Reverse Mortgage：Contractions and Crossover Risk[J].Journal of American Real Estate and Urban Economics Association,1994(2):367～386．

[3]Olivias Mitchell，John Piggott, Unlocking Housing Equity in Japan[J].Journal of Japanese Int．Economics,2004(18):466～505．

[4]Bardhan，Karapanda，Urosevic,Valuing Mortgage Insurance Contracts in Emerging Market Economies[J].Journal of Real Estate Finance and Economics,2006(32):9～20．

[5]Seungryul Ma.,Gabtae Kim&Keunoak Lew,Estimating Reverse Mortgage Insurer’s Risk Using Stochastic Models[R].Conference of Asia-Pacific risk and Insurance Association,Taipei,Taiwan,2007:22～25.

[6]刘春杰，谭竞.反抵押贷款支付额度的确定[J].浙江金融,2005，(5):19～20．

[7]奚俊芳.反向抵押贷款定价模型研究[D].上海：华东师范大学，2007.

[8]范子文.“以房养老”住房反向抵押贷款的国际经验与现实选择[M].北京：中国金融出版社，2006.

[9]柴效武.反向抵押贷款产品定价[M].杭州：浙江大学出版社，2008.

[10]陈秉正，秦鹏，邓颍璐.具有赎回选择权的住房反抵押贷款定价[J].投资研究,2014，(5):97～109.

[11]陈秉正，秦鹏，邓颍璐.具有长期护理保障功能的住房反抵押产品研究[J].保险研究,2014，(5):49～59.