正弦机构在球面展开中的运用

2015-05-10 05:52龚凌云

龚凌云

（广州铁路职业技术学院机电工程学院，广东广州 510430）

1 引言

实现钢球表面展开也就使钢球在展开机构的作用下，连续、高速的运动，并将其表面各区完全的送到传感器下进行检测，在这一过程中球表面不能有盲区。钢球表面展开运动实际上是钢球受两套独立驱动机构的作用，完成一种比较复杂空间螺旋运动。本文利用正弦机构原理提出了一种新的球面运动展开方法。

正弦机构如图1所示。在此机构中，从动件2与3（实为钢球，其球心固定不动）只有滚动而无滑动，故为同步运动[1]。从动件2与原动件1的转角α的正弦成正比，即

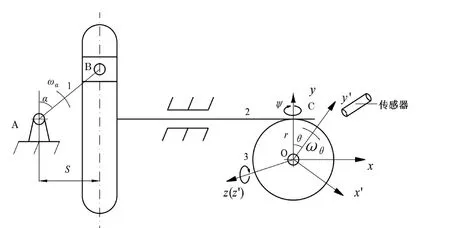
图1 正弦机构

上式中， lAB为杆AB的长度，α为杆AB的转角，ωα为杆AB的转动角速度， t为转动时间。对从动件3而言，则有：

上式中，r为球O的半径，θ为球O的转角。

由（2）式可得：

由此可知，当主动件1匀速转动时，钢球的转角θ是按正弦规律变化的，转角θ的最大值θmax取决于杆 AB的长度lAB与钢球的半径r，即

正弦机构实现了球绕Oz的来回偏转，如果球同时绕Oy回转，那么就能实现球体的偏转，即也就实现球面的运动展开，即为球面的运动展开法。

钢球在展开运动中，钢球的球心O在空间的位置保持不变。选取O-xyz为固定坐标系，取O-x’y’z’为动坐标系与球固结，在初始位置与固定坐标系重合。如图1所示。球绕固定坐标系Oy旋转的同时，绕Oz旋转，球绕Oy’与绕Oz’的转角分别为ψ和θ。

钢球在这整个运动过程中必须连续。因此，球对这两个轴的转动是有规律地定时重复，这样球面上一点运动的轨迹曲线才能是闭合的[2]。在正弦机构的作用下，θ绕Oz’(Oz)规律做往复运动，即

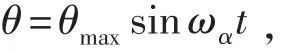
角速度大小

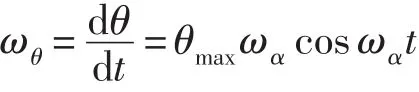
角速度矢量方向与OZ’(OZ)轴一致。转角ψ为钢球绕OY’轴在匀速运动时发生的转角，即ψ=ωψt，ωψ为钢球绕Oy/轴在匀速运动时的角速度，角速度矢量方向与Oy/轴一致。

钢球上点的位置用矢量r表示，设半径为R球面上一点P的初始坐标为(x0，y0，z0)，经时间t变换后的坐标为(x，y，z)。则有

球面上P点的瞬时速度

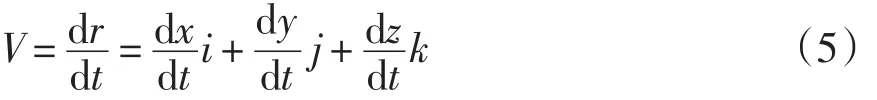
而

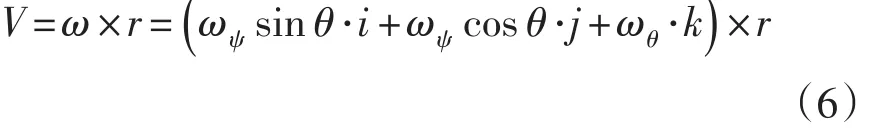
由以上二式得：

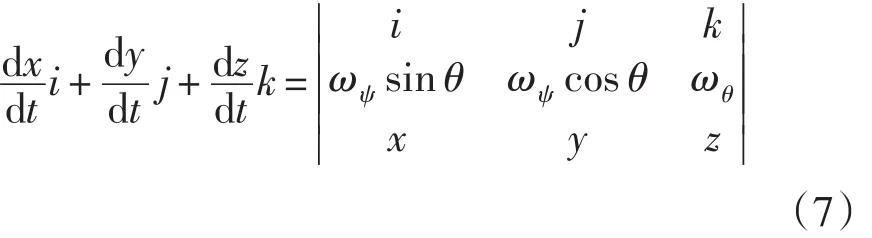
可知运动学方程为：

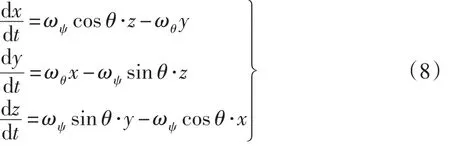
而动坐标系O-XYZ与静坐标系O-X/Y′Z′之间的转换矩阵为

球做自转运动时，其上的任一点的坐标变换矩阵为

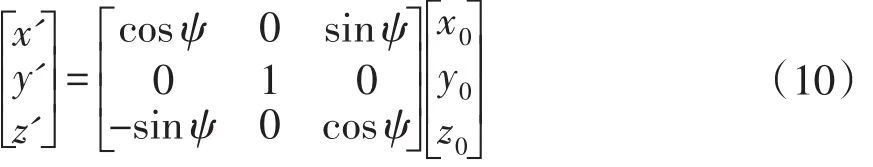
将（10）式代入（9）式，并引入初始解条件（（x ， y，z|t=0=(x0，y0，z0)，可得P点运动的轨迹方程即

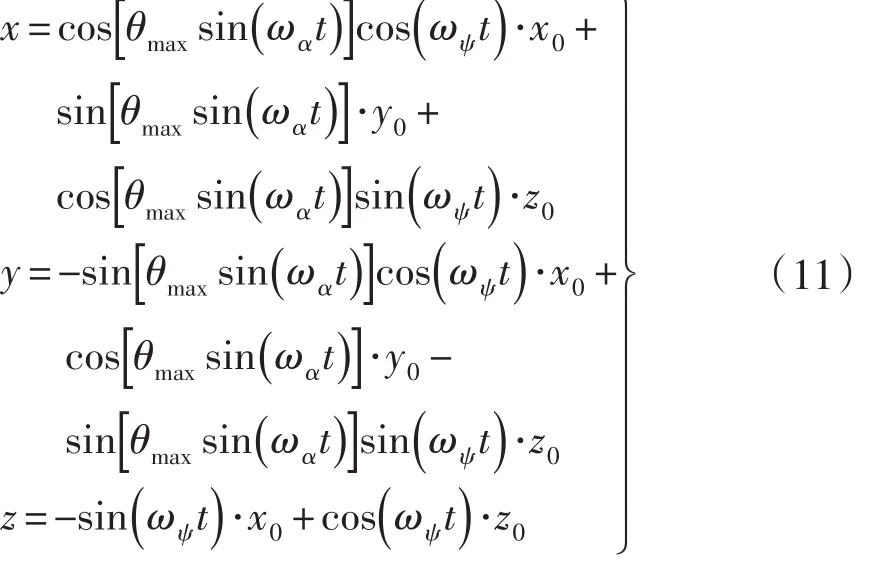
（11）式精确地给出了钢球在正弦机构(ωα)与匀速运动机构(ωψ)综合作用下，其上的一点P(x0，y0，z0经过时间t后，运动到球面上另一点（x，y，z）处的运动学方程。这一研究为钢球展开机构的优化提供了必要的数学工具与理论基础。

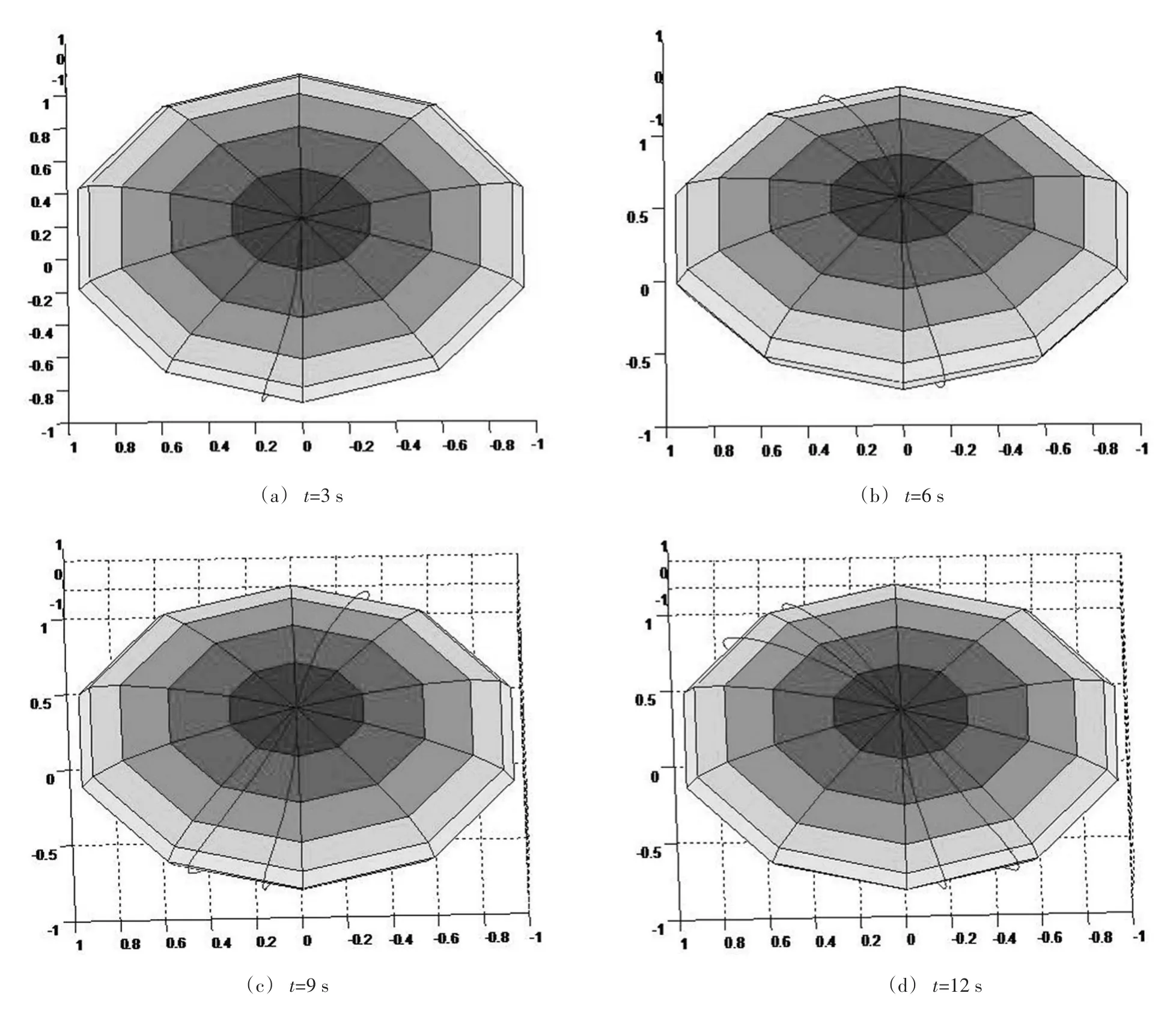
图2 不同时刻P点的运动轨迹

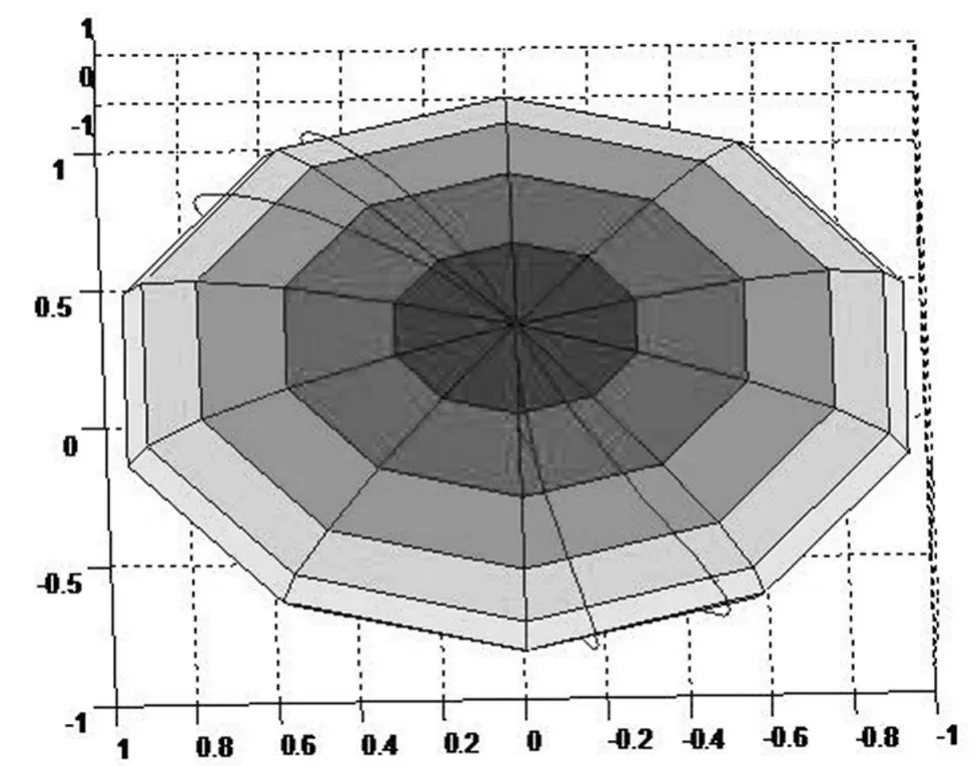
图3 P点的综合运动轨迹图

本文利用展开轮推动钢球转角呈现正弦规律变化的趋势，得出了钢球运动变化的解析式（11）。为实现钢球展开机构的优化，以此两种特定的运动定量地研究钢球的运动规律，建立一套更为准确、有效、简便的数学工具是本文研究的重点。

为了验证（11）式的正确同时利用MATLAB的数值计算功能和函数可视化功能，根据上面所提供的解析式得出球面上P点在不同时刻的运动轨迹图如图2所示。当球按照上述运动规律连续运动，直至完成一次全面展开，球面上P点的运动轨迹如图3所示，可以看出时间化分得越小，P点的运动轨迹包络成的曲线就是一个球面。

［1］苏步青，华宣积，忻元龙.实用微分几何引论［M］.北京：科学出版社，1986.

［2］J.B.Marion.质点与系统的经典动力学［M］.北京：高等教育出版社，1985.