基于多边形最佳平方逼近形式的边坡稳定上限有限元法

何玉红

(濮阳职业技术学院 建筑工程系, 河南 濮阳 457000)

基于多边形最佳平方逼近形式的边坡稳定上限有限元法

何玉红

(濮阳职业技术学院 建筑工程系, 河南 濮阳 457000)

边坡的极限分析上限法具有较严谨的理论基础和物理意义，且可以在得到安全系数的同时找到最危险的临界失稳速度场，因此具有较广阔的应用前景。针对目前上限有限元法中被广泛采用的外切多边形逼近摩尔库伦屈服圆所带来的收敛速度慢的缺点，放松边坡内任一点需严格满足上限性质的要求，将多边形采用最佳平方逼近的形式逼近屈服圆，并系统地推导出了最佳平方逼近形式的上限有限元法的整个计算模型。算例表明：该方法不仅继承了外接多边形从上方逼近解析解的优点，而且采用较少的多边形边数即可得到较为精确的结果，收敛速度大大提高。

极限分析；上限有限元法；摩尔库伦屈服圆；多边形最佳平方逼近；解析解；边坡稳定

1 研究背景

目前常用的边坡稳定性分析方法主要有极限平衡法和有限元强度折减法。极限平衡法虽然概念简单，易于被工程师掌握，但为了消除问题的不静定性，引入了大量假设，力学性质上缺乏严密性。不同的条间力关系假设形成了不同的极限平衡法，如Janbu法、MP法等；再者，极限平衡条分法的数值特性较差，有的算例表明，不同的条分法结果相差达35%[1]。有限元强度折减法虽能在一定程度上弥补极限平衡法的不足，可以考虑边坡的应力应变关系，但其对边坡进入极限状态的判据尚未达成统一[2-3]。事实上，工程中我们关心的并不是边坡失稳破坏的整个过程，而是它的安全程度如何，以及可能产生破坏的临界滑动面是怎样构成的，即边坡的破坏方式和破坏范围有多大。极限分析能有效地解决这一问题，它最大的优点就是回避了工程中较为模糊的本构关系，放松力或者位移的约束，直接研究边坡的极限状态，从不同角度去逼近真实解。极限分析理论在1951年被Drucker等[4]首次提出，1975年，陈惠发等[5]阐明和论述了其在土工问题中的应用，随后，极限分析理论被学者们广泛研究，成为了土工领域解决问题的有力工具。最初的极限分析上限法仍需要划分条块，R.L.Michalowski[6]，Orang Farzaneh等[7]和陈祖煜等[8]分别采用这一模式对边坡的稳定性进行过分析，该方法对特定破坏模式的研究十分有效，但当边界条件复杂时将难以进行。S.W.Sloan[9-10]在前人工作的基础上，将有限元和线性规划技术结合起来应用到了极限分析上限法之中，考虑单元之间相邻边上的速度间断条件，提出了用外切多边形来逼近摩尔库伦屈服圆，将非线性规划问题巧妙地转化成了线性规划问题。国内学者中王均星[11]、杨小礼[12]、王敬林[13]等均是沿着这一思路进行极限分析上限法的研究。

我们注意到，在用外切正多边形对屈服圆逼近的时候，只有多边形的边数足够多时，才能得到合理的结果，这就造成了约束方程的未知变量过于庞大，严重影响计算的效率。其实，从本质上来讲，只要所求极限荷载是从它的上方收敛的，就是它的一个上限解，从这点出发，我们放松上限法需严格满足上限性质的约束，对正多边形采用最佳平方逼近的形式来逼近摩尔库伦屈服圆，得到了新的线性拟合方程。算例表明该逼近方式可以大大提高收敛速度，且具有和外接多边形相同的收敛值。

2 极限分析上限法基本原理

假设结构物有多种破坏形式，且每个机动容许的速度场对应着一个外荷载，则在所有的与机动容许速度场对应的荷载中，最小的荷载即为极限荷载，与最小荷载对应的机动容许速度场为破坏速度场。

把上限定理写成数学模型，即为

(1)

3 最佳平方逼近多边形方程

对平面应变问题，假设拉正压负，摩尔库伦屈服准则可表示为

F=(σx-σy)2+(2τxy)2-

[2ccosφ-(σx-σy)sinφ]2=0 。

(2)

式中c和φ分别为土体黏聚力和内摩擦角。在以σx-σy为x轴、2τxy为y轴的坐标系中，摩尔库伦屈服函数为1个圆，圆心位于原点，半径为

R=2ccosφ-(σx+σy)sinφ。

(3)

如图1，当采用外切正p边形对屈服圆进行逼近时，那么容易求出每条边的方程表达式为

Fk=Akσx+Bkσy+Ckτxy-Dk。

(4)

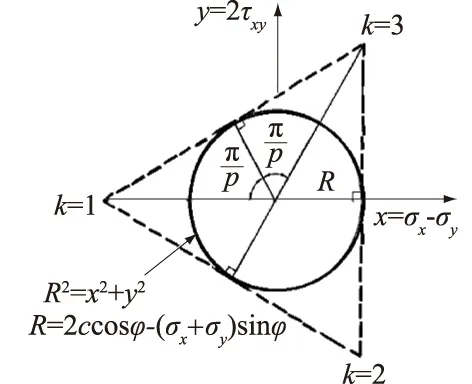
图1 外切多边形逼近摩尔库伦屈服圆(p=3)Fig.1 Circumscribed polygon approximation to the Mohr-Coulomb yield circle (p=3)

式中：

(5)

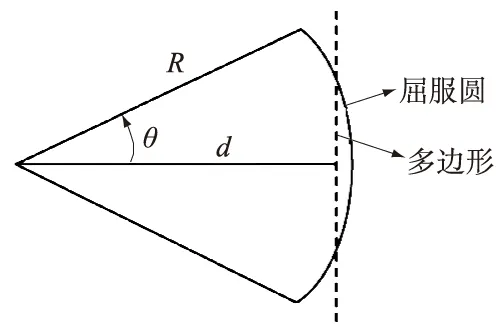
图2 最佳平方逼近模型Fig.2 Model of optimal square approximation

在求解最佳平方逼近屈服圆每条边的方程之前，首先需要介绍最佳平方逼近的基本概念：对于已知函数f(x)，x∈[a，b]，令Qn为由 {1,x,x2,…,xn}构成的n+1维空间，如果P*(x)∈Qn，且满足

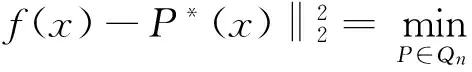
则称P*(x)为f(x)在[a，b]上的最佳平方逼近多项式[14]。

如图2所示，为一极坐标下屈服圆的一部分，d为圆心到多边形一条边的距离，R为屈服圆半径，若以θ为自变量，且多边形边数为p，则最佳平方逼近多边形一条边的方程在极坐标系下可写为

r=d/cosθ。

(7)

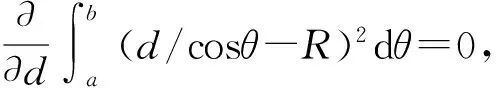
(8)

因为最佳平方逼近多边形的内切圆半径R′=d，用R′替换R即可求得最佳平方逼近多边形的每条边方程表达式为

(9)

式中:

(10)

4 单元内最佳平方逼近多边形塑性流动约束方程

对于理想刚塑性体，相关流动法则结合线性化的摩尔库伦屈服准则可表示为

(11)

(12)

将式(9)、式(10)和式(12)代入式(11)可得矩阵形式表示的塑性流动约束方程，即

a11x1-a12x2=0 。

(13)

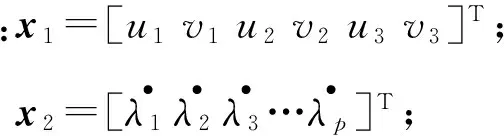
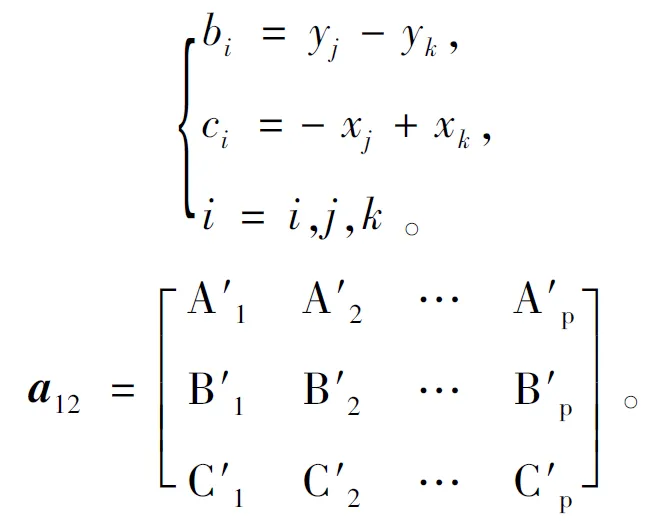
式中：Ae为三角形单元面积；(xi，yi)为节点坐标;T表示求转置;(u,v)为速度间断点坐标。

5 其他约束方程

5.1 速度间断线上约束方程

如图3所示，节点1,2和3,4所在的速度间断线与x轴夹角为θ,则对于摩尔库伦屈服准则，速度间断线上的法向Δv与切向Δu相对速度满足

Δv=|Δu|tanφ。

(14)

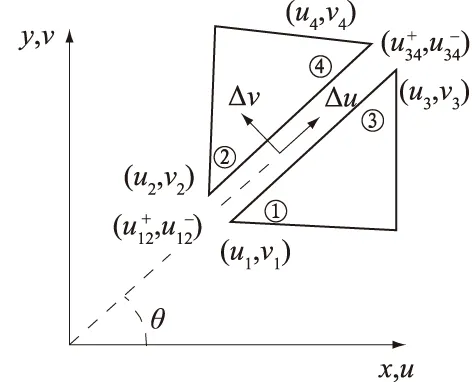
图3 三角形单元速度间断线Fig.3 Velocity discontinuity of triangle element

参照文献[10]，对每对速度间断点引入非负变量u+和u-，且满足

(15)

将式(15)代入式(14)，为了去除速度间断线上的塑性流动方程中的绝对值符号，在求解法向相对速度Δv时， 用(u++u-)代替|u+-u-|可得

(16)

于是，对于每条速度间断线，需要施加的塑性流动约束条件为

a21x1-a23x3=0 。

(17)

式中a21，a23分别为坐标转换矩阵和参数矩阵，表达式见文献[10]。

5.2 速度边界条件

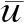
a31x1=b。

(18)

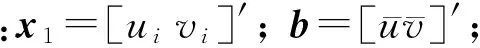
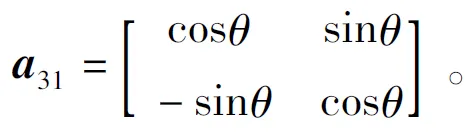
5.3 外力功率及内部耗散功率

5.3.1 单元内部耗散功率

每个单元内部的耗散功率Pc为

(19)

将式(11)代入式(19)，可得

(20)

将式(20)写成矩阵的形式，即

Pc=c2x2。

(21)

式中c2=2Aeccosφ[l1l2…lp]。

5.3.2 速度间断上耗散功率

每条速度间断线上的耗散功率Pd为

(22)

式中l为间断线长度，令Δu=u++u-,则式(22)写成矩阵形式，即

Pd=c3x3。

(23)

式中c3=0.5cl[1 1 1 1]。

5.3.3 外力功率

外力功率是塑性流动刚发生时，所有外部荷载对破坏区域的速度场所做的功率。现仅以体力为例进行说明，如

(24)

对于三角形单元，由于体力在单元内部为线性分布，于是式(24)可写成

Pt=c1x1。

(25)

式中c1=-γ/3[0Ae0Ae0Ae]。

6 上限有限元法数学模型

在得到了上限有限元的所有约束条件后，根据功率平衡方程可得到目标函数，即耗散能减去外力功率的差值，优化变量为单元节点速度分量、塑性乘子及速度间断线引入的辅助变量。

根据参考文献[15]的做法，对强度参数进行调整，使超载系数逼近于1，从而可以得到不易直接求解的强度折减系数。由于我们求解的只是破坏时结构的破坏形式，它仅与x1的相对大小有关，因此令c1x1=1，此时上限有限元的规划模型可表示为:

Min:c2x2+c3x3。

(26)

(27)

7 算 例

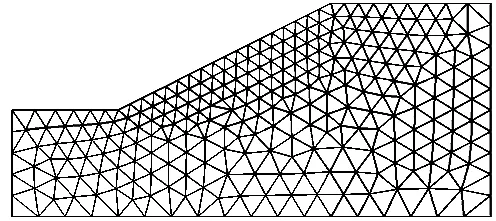
图4 边坡网格划分Fig.4 Meshing of the slope

本文算例的优化模型是借助于Matlab来求解的。一均质边坡，引自文献[16]，坡比为1∶2，坡高20m，重度γ=16 kN/m3，黏聚力c=20 kPa，内摩擦角φ=20°，网格划分如图4所示。

当多边形边数分别采用4，8，15，20，30时，2种屈服圆逼近形式得到的结果如表1和图5。

表1 不同边数正多边形逼近时的安全系数Table 1 Safety factor in the presence of different edge numbers of regular polygon

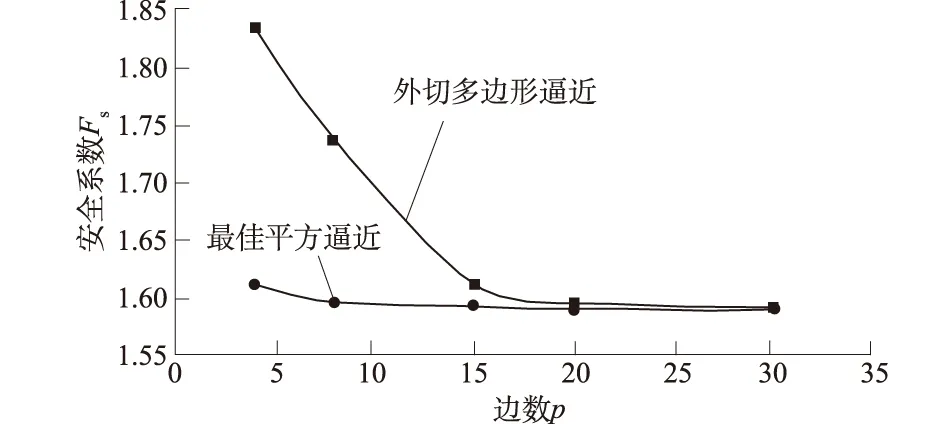
图5 安全系数Fs与多边形边数p的关系Fig.5 Curves of safety factor Fs vs. edge number p

从图5可以看到，上限有限元中，在进行屈服圆线性化时，多边形采用最佳平方逼近的形式收敛速度非常快，在边数p=8时，即可达到一定的收敛要求，而采用外切多边形逼近时，达到相同的精度多边形边数p需取20，这就大大增加了耗时，减少了计算效率。文献[16]对本算例采用M-P方法并取正弦条间力函数时得到的安全系数为1.588，用Spencer法得到的安全系数为1.589，均与本文上限法最终收敛结果1.589较为接近，说明了本文方法的有效性。

图6为p=8时，采用多边形最佳平方逼近的边坡极限状态失稳速度场，从图6中可以清晰地看出边坡的临界滑动面及破坏模式，这可为后续的边坡支护提供帮助。

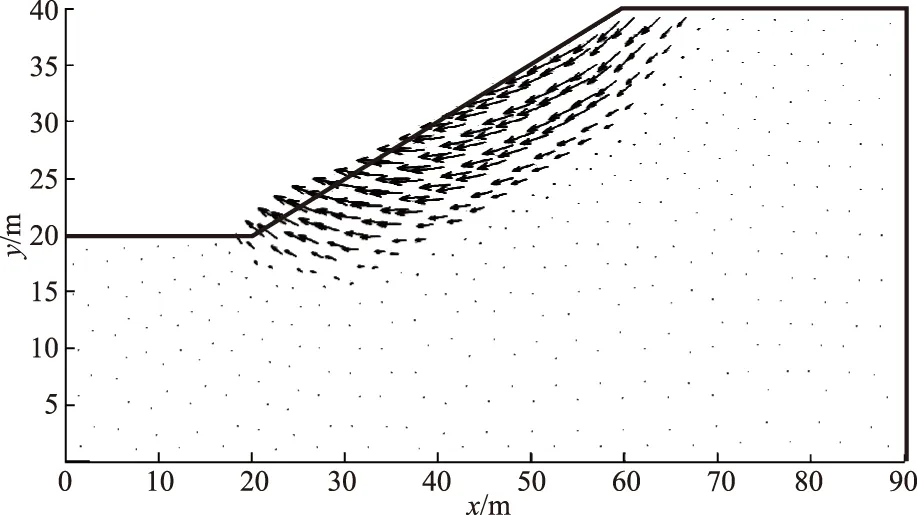
图6 边坡极限状态失稳速度场Fig.6 Velocity field of the slope’s limit state

8 结 论

(1) 极限分析上限法具有较强的理论基础和物理意义，从边坡破坏的角度出发，通过优化求解在得到边坡安全系数的同时，还可以得到最易失稳的破坏形式和速度场，具有较广阔的应用前景。

(2) 针对外接多边形线性化拟合MC屈服圆所形成的性规划模型求解效率慢、待优化变量过多的问题，放松边坡内任一点均需满足上限性质的约束，将多边形通过最佳平方逼近的形式逼近MC屈服圆，推出了最佳平方逼近多边形每条边的函数方程，并得到了单元内的新的塑性流动约束条件。算例表明该方法不仅继承了外接多边形从上方逼近解析解的优点，而且求解规模更少，收敛速度大大提高，节约时间成本，建议在工程运用中推广。

[1] YU H S, SALGADO R, SLOAN S W,etal. Limit Analysis Versus Limit Equilibrium for Slope Stability[J]. Journal of Geotechnical and Geoenvironmental Engineering, 1998, 124(1): 1-11.

[2] GRIFFITHS D V, LANE P A. Slope Stability Analysis by Finite Elements[J]. Geotechnique, 1999, 49(3):387-403.

[3] 宋二祥. 土工结构安全系数的有限元计算[J]. 岩土工程学报, 1997, 19(1):1-7.(SONG Er-xiang. Finite Element Analysis of Safety for Soil Structure[J]. Chinese Journal of Geotechnical Engineering, 1997, 19(1):1-7.(in Chinese))

[4] DRUCKER D C, GREENBERG H J, PRAGER W. The Safety Factor of an Elastic-plastic Body in Plane Strain[J]. Journal of Applied Mechanics Transactions of the ASME, 1951, 18(4): 371-378.

[5] CHEN W F. Soil Mechanics and Theorems of Limit Analysis[J]. Journal of Soil Mechanics & Foundations Division, 1969, 95(2): 493-518.

[6] MICHALOWSKI R L. Slope Stability Analysis: A Kinematical Approach[J]. Geotechnique, 1995, 45(2):283-293.

[7] FARZANEH O, ASKARI F. Three Dimensional Analysis of Nonhomogeneous Slopes[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2003, 129(2): 137-145.

[8] 陈祖煜.土质边坡稳定分析[M].北京:中国水利水电出版社，2003. (CHEN Zu-yu. Stability Analysis on Soil Slope[M]. Beijing: China Water Power Press, 2003. (in Chinese))

[9] SLOAN S W. Upper Bound Limit Analysis Using Finite Element and Linear Programming[J]. International Journal of Analytical Methods in Geomechanics, 1989,13(3): 263-282.

[10]SLOAN S W. Upper Bound Limit Analysis Using Discontinuous Velocity Fields[J]. Journal of Computer Methods in Applied Mechanics and Engineering, 1995, 127(4): 293-314.

[11]王均星，王汉辉，张优秀，等.非均质土坡的有限元塑性极限分析[J].岩土力学，2004，25(3):415-421.(WANG Jun-xing, WANG Han-hui, ZHANG You-xiu,etal. Plastic Limit Analysis of Heterogeneous Soil Slope Using Finite Elements[J]. Rock and Soil Mechanics, 2004, 25(3):415-421. (in Chinese))

[12]杨小礼，李 亮，李克坤.上限原理法及其在陆地稳定性分析中的应用[J].长沙铁道学院学报，2002，20(l):41-45. (YANG Xiao-li, LI Liang, LI Ke-kun. Bearing Capacity Analysis of Subgrade Soil Using Upper Bound Finite Element Method[J]. Journal of Changsha Railway University, 2002, 20(l):41-45. (in Chinese))

[13]王敬林，钱开东，陈壁强.广义塑性理论上限法及其在边坡工程中的应用[J].重庆建筑，2002，(2):20-23. (WANG Jing-lin, QIAN Kai-dong, CHEN Bi-qiang. Generalized Plastic Upper Bound Method and Its Application in Slope Engineering[J]. Chongqing Architecture, 2002, (2):20-23. (in Chinese))

[14]李庆扬，王能超，易大义. 数值分析[M]. 北京：清华大学出版社，2001. (LI Qing-yang, WANG Neng-chao, YI Da-yi. Numerical Analysis[M]. Beijing: Tsinghua University Press, 2001. (in Chinese))

[15]李国英, 沈珠江.下限原理有限单元法及其在土工问题中的应用[J]. 岩土工程学报, 1997, 19(5): 84-89. (LI Guo-ying, SHEN Zhu-jiang. Lower Bound Finite Element Method and Its Application in Geotechnical Problems[J]. Chinese Journal of Geotechnical Engineering, 1997, 19(5): 84-89. (in Chinese))

[16]ABRAMSON L W, LEE T S, SHARMA S. Slope Stability and Stabilization Methods[M]. New York: Wiley, 1996.

(编辑：姜小兰)

Upper Bound Finite Element of Slope Analysis Based onOptimal Square Polygon Approximation

HE Yu-hong

(Department of Building Engineering, Puyang Vocational and Technical College, Puyang 457000, China)

The upper bound limit analysis has broad application prospect as it has rigorous theoretical basis and clear physical meaning, and could give the safety factor as well as the critical velocity field at the same time. But it has slow convergence speed because of circumscribed polygon approximation (which is widely used) to Mohr-Coulomb yield circle. In view of this, we alleviated the requirement that all the points must strictly meet the limit properties, adopted the optimal square polygon approximation to the yield circle, and finally obtained the systematic calculation model of upper bound finite element based on optimal square polygon approximation. Numerical example shows that the method not only inherits the advantage circumscribed polygon have which approximates analytic solution from the upper, but also gets a precise result by less number of polygon edges, and also greatly improves the convergence speed.

limit analysis; upper bound finite element method; Mohr-Coulomb yield circle; optimal square approximation; analytical solution; slope stability

2014-03-08；

2014-04-30

何玉红(1970-)，女，河南濮阳人，副教授，国家注册造价师，主要从事土木工程计算方面的研究，(电话)15203935876(电子信箱)heyuhong000@163.com。

10.3969/j.issn.1001-5485.2015.08.015

TU47

A

1001-5485(2015)08-0084-05

2015,32(08):84-88