步进梁液压控制系统PID参数的整定与优化

(中冶南方工程技术有限公司 热轧分公司， 湖北 武汉 430223)

引言

步进式加热炉是热轧厂中使用最广、发展最快的一种连续式加热炉。步进梁运动负载大，一般采用液压驱动。步进梁运动要求周期短、运行平稳，同时还要保证位置精度，对液压控制系统的设计提出了较高的要求。

以某热轧厂升降液压缸控制系统作为研究对象，建立其闭环位置控制系统的动态数学模型。针对位置和速度控制要求较高的特点，采用Ziegler-Nichols法和遗传算法对升降液压缸控制系统的PID参数进行整定，通过比较得出最优的控制参数。

1 步进梁的传动机构及液压原理图

步进梁传动机构按矩形轨迹运动，一个运动周期由4个动作组成：上升、前进、下降、后退。大中型步进加热炉多采用斜块滑轮式，主要由上动梁、下动梁、升降斜轨、液压驱动机构等组成。如图1所示。

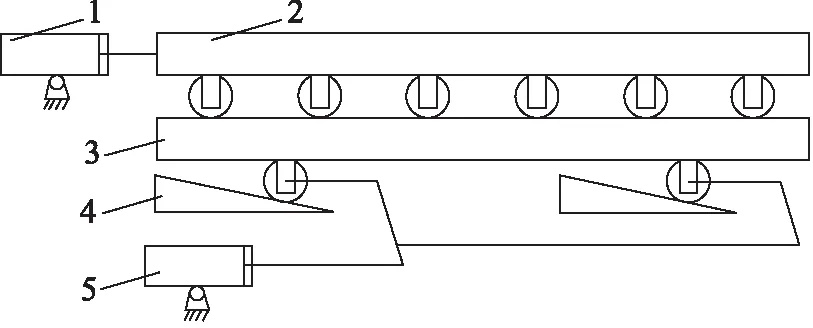
1.横移液压缸 2.上动梁 3.下动梁 4.升降斜轨 5.升降液压缸图1 步进加热炉传动机构示意图

为了实现步进动梁平稳地启动、加速、减速、停止，即在动梁上升或下降到与固定梁相平时，运动速度要较慢，以便轻抬或轻放钢坯，防止冲击；当上升到最高点时要减速，移动时运动要平稳，防止钢坯产生晃动。

图2为升降液压缸液压原理图，系统的流量大，采用插装式二通比例流量阀。两升降液压缸采用机械同步，通过两缸驱动滚轮沿着斜轨作升降运动。

图2 升降液压缸液压原理图

2 液压控制系统建模及动态分析

在升降液压缸液压系统中，液压缸处均设有位移传感器，用来对液压缸的位置进行精确检测和反馈，是典型的位置反馈控制系统。

频率特性分析是经典控制理论中研究与分析系统的主要方法。为了通过频率特性来分析该系统，现将该步进梁液压系统中的相关参数带入闭环比例控制系统模型中，得出系统在Simulink中的开环模型框图(如图3)及系统开环Bode图(如图4)。

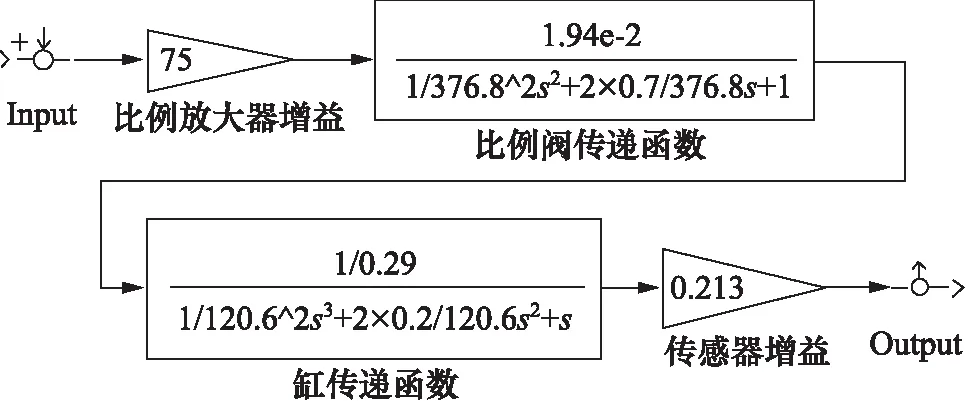
图3 系统在Simulink中的开环模型框图

从图4可以看出，该系统的幅值裕度为32.3 dB，相位裕度为89.6°，闭环系统是稳定的。

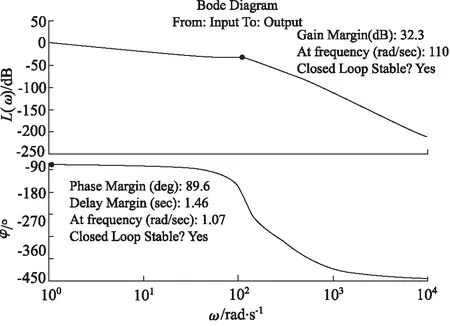
图4 系统的开环Bode图

在工控领域，为达到较好的控制效果，要求系统具有一定的稳定裕量，通常要求：幅值裕度大于6 dB，相位裕度在30°～70°之间。该系统相位裕度大，导致系统动态响应慢，应对其进行适当校正以改善系统性能。

3 闭环控制系统PID参数的整定

PID控制器由于其机构简单，操作方便、可靠性高，被广泛应用于冶金、机械等工业过程控制中。PID成传递函数的形式为：

(1)

式中，Kp为比例系数；Ti为积分时间常数；Td为微分时间常数。

3.1 Ziegler-Nichols法的PID整定

根轨迹法与伯德图设计的方法均不能被直接用于PID整定。Ziegler与Nichols发展了PID调节器设计方法，该方法基于简单的稳定性分析方法。设Ti=∞,Td=0,只采用比例控制作用，使Kp从0增加到临界Kc，其中Kc是使系统的输出首次呈现持续震荡的增益值。其他参数根据Ziegler-Nichols调整法则确定，如表1所示。

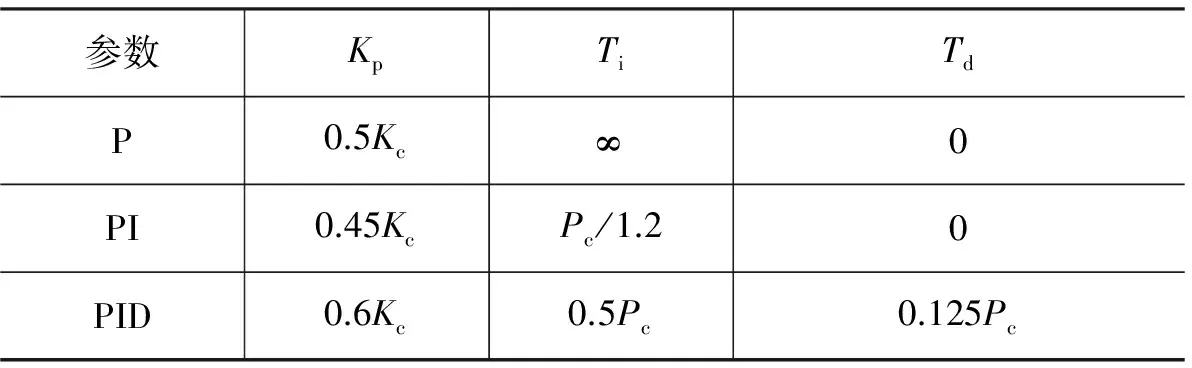
表1 基本临界增益和临界周期的

(2)

式中，Kc为系统开始振荡时的比例系数值；ωm为振荡频率；Pc为临界振荡周期。

在MATLAB中，通过调用命令rlocus()，得到如图5所示的根轨迹图，与jω轴相交点的增益值41.4就是Kc值，此时的振荡频率ωm值为110 rad/s,将Kc及ωm值代入式(2)得：Kp=24.84，Ki=870.2，Kd=0.1773。

图5 系统的根轨迹图

为了得出校正后的阶跃响应，在Simulink中建立系统PID校正闭环模型框图(如图6)，其阶跃响应如图7所示。经过Ziegler-Nichols法PID整定校正后，系统阶跃响应的上升时间为0.0181 s，系统停留在稳态值±2%内的时间为0.302 s，并达到稳定值。

可见，在保证系统快速响应中，Ziegler-Nichols法PID整定的确是一种好的经验方法。然而系统超调较大，最大超调量为57.3%。对于步进梁而言，将会造成较大的冲击，因而应尽量避免。

图7 Ziegler-Nichols法PID整定后的阶跃响应

3.2 遗传算法的PID整定

在PID控制器中，需要优化的参数为：比例系数Kp、积分系数Ki和微分系数Kd。根据Ziegler-Nichols法PID整定的参数值，可以大概设置三个参数的取值范围：Kp∈[0,50]，Ki∈[0,10]，Kd∈ [0,1]。

个体适应度评价，即根据优化目标设计出目标函数，映射为适应度函数后，然后按个体的适应度函数值(即适配值)来进行评价，适配值越大，适应度越好。对于PID参数取值的优劣，可由偏差积分指标衡量。常用的指标有如下几种：

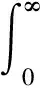
对于本控制系统，为了抑制过程中的小偏差，采用IAE形式作为目标函数的指标之一，加入调整时间项来缩短系统的调整时间。另外，为防止控制能量过大，在目标函数中加入输入的平方项。选用下式作为参数选取的最优指标：

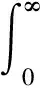
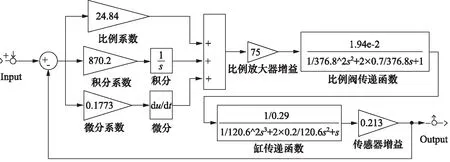
图6 Simulink中PID校正闭环模型框图

式中，e(t)为系统误差；u(t)为控制器的输出；ts为系统调整时间；w1、w2、w3为调整权值。

为控制超调的大小，加入惩罚控制，一旦系统产生超调，将超调量作为最优指标的一项，此时最优指标为：

Ifey(t)<0，

w4ey(t))dt+w3·ts

式中，w4为权值；y(t)为被控对象的输出，且w4>>w1，ey(t)=y(t)-y(t-1)。

选取初始种群中的样本个数Num=30，遗传终止代数G=200，交叉概率Pc=0.90，变异概率Pm=0.10-[1∶1∶Num]×(0.01)/Num。对于w1、w2、w3、w4四个权值，根据优化的结果调整后，确定取w1=12、w2=0.1、w3=100、w4=1000，采样时间为0.5 s。运行程序，目标函数优化过程如图8，在遗传约130代时收敛，PID整定结果为：Kp=20.9828，Ki=0.0377,Kd=0.4728。

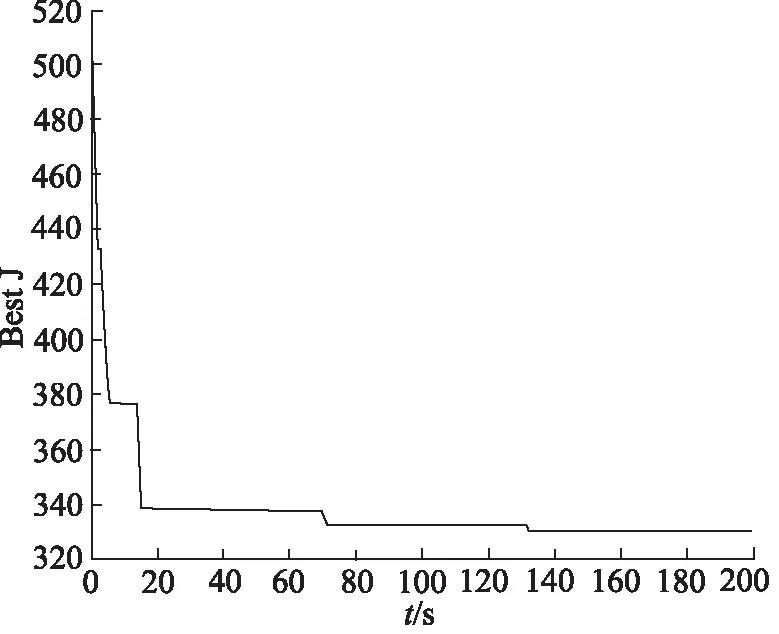
图8目标函数的优化过程

现对比一下两种PID整定方法的阶跃响应，如图9。从阶跃响应的曲线来看，遗传算法PID整定的结果响应比较平稳，几乎没有超调，明显优于Ziegler-Nichols法PID整定的结果。

经过遗传算法的PID校正后，系统的开环Bode图如图10所示。可见，系统的幅值裕度为7.4 dB，相位裕度为82°，闭环系统稳定。与为校正前相比，相位裕度由89.6°变为82°，系统稳定时间缩短。最后确定PID参数为：Kp=20.9828，Ki=0.0377,Kd=0.4728。

可见，遗传算法PID整定操作简单，能够并行对参数实现优化，是一种高效的搜索方式。在合理设计目标函数的前提下，遗传算法能很快得到参数的最优值，具有很强的实用性。

图9 两种方法PID整定结果阶跃响应

图10 PID校正后系统开环Bode图

4 基于MATLAB和AMESim的联合模拟仿真

在工程领域中,Simulink已发展成为主流的仿真软件，然而其仿真效率过低。现在，可以利用AMESim和MATLAB的接口技术，将AMESim强大的流体仿真能力与MATLAB强大的数字处理能力联合起来使用，效果更好。

在控制过程中，PLC根据液压缸动作所需流量给比例阀以相应的电流信号。AMESim中可调用数字量化模块对模拟信号进行数字化，通过设置阶梯的幅度，就可以实现信号的阶梯式输入，模拟PLC的给定信号。在计算处理方面，MATLAB更加可靠，为了不失准确性，直接将MATLAB中经校正后的线性系统导入到AMESim中，进行联合仿真。

设置AMESim和MATLAB的接口后，在MATLAB中，将系统中的PID校正环节、比例放大器、比例阀串联成传递函数sys,然后分别输入[num,den]=tfdata(sys,‘v’)和tf2ame(num，den，‘function.ssp’)命令，function.ssp即为可以被AMESim直接调用的文件。在AMESim环境中，通过菜单Modeling/Import linear model将该文件导入后，出现如图11所示的对话框，进行相关输入后，建立系统的闭环模型如图12所示。

图11 导入线性模型对话框

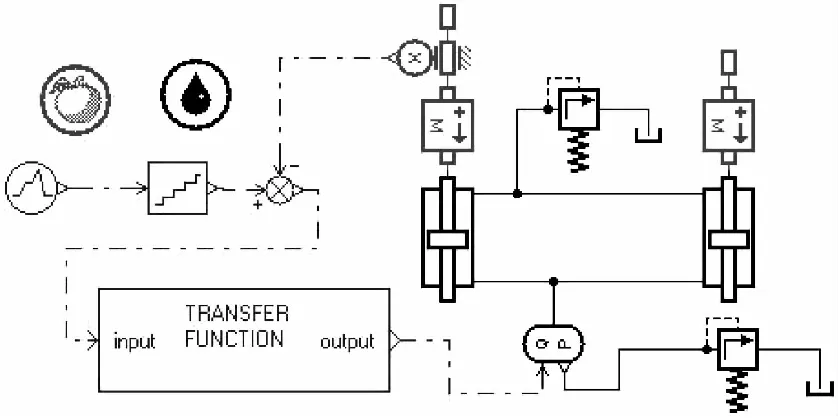
图12 AMESim中闭环系统框图

二通插装比例阀的输入信号为4～20 mA,可调范围为0～16 mA。该比例阀的灵敏度小于0.1%，阶梯信号的梯度增量设置为0.2 mA；将升降压缸动作各阶段所需流量换算成比例阀的给定信号，经模块量化后，阀的阶梯电流信号如图13所示，在16 s内完成上升的动作。设置好提升缸的相关参数及位移传感器的增益，为了较清楚观察该阶梯信号，提取前1.8 s的电流阶梯信号，如图14。运行仿真后，可得升降液压缸的优化速度曲线如图15所示。

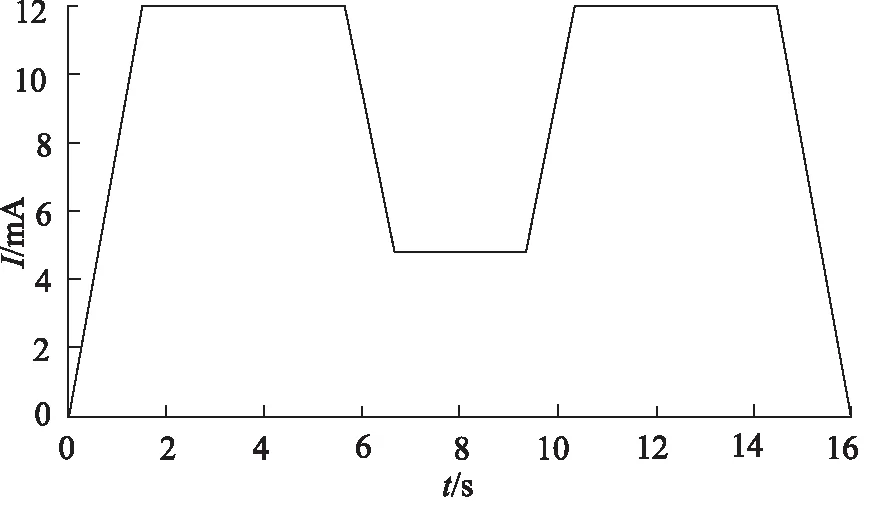
图13 阶梯电流信号

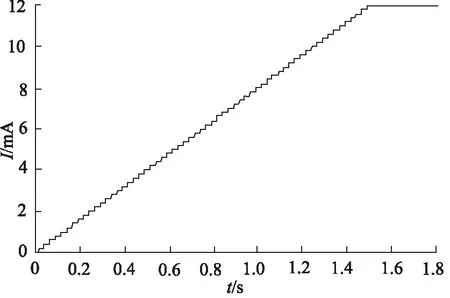
图14 0～1.8 s的阶梯电流信号

图15 升降液压缸上升速度图

升降液压缸能按照设计的要求，在规定的时间内，完成上升运动过程中的加速、定速、减速等动作，并且速度的过渡平稳。可见，该设计可靠性强、自动化程度高，很好地满足了工况的要求。

5 结论

可见，Ziegler-Nichols法整定的结果为遗传算法对PID三个参数的搜寻范围提供了参考，减少了遗传算法搜寻的盲目性。

最后运用MATLAB和AMESim进行了联合模拟仿真，得出了液压缸的优化速度曲线，证明了遗传算法的寻优功能。另外，联合仿真为系统的设计提供了一个很好的实验平台，具有很强的研究指导意义。

参考文献：

[1] 杨叔子,杨克冲.机械工程控制基础[M].武汉:华中科技大学出版社,2000.

[2] 刘金琨.先进PID控制MATLAB仿真[M].北京:电子工业出版社,2007.

[3] 付永领，祁晓野.AMESim系统建模和仿真——从入门到精通[M].北京:北京航天航空出版社,2006.