水土耦合对盾构土拱效应及最小支护力的影响分析

宋锦虎，陈坤福，李宁娜，梁 静

(1. 河南城建学院 土木工程学院，河南 平顶山 467044；2. 中国矿业大学 力学与建筑工程学院，江苏 徐州 210096)

近年来，由于各大城市交通压力的增加及土地资源的稀缺，地铁和地下通行隧道成为主要解决措施。但由于开挖面支护力控制不当导致地表过大沉降及地表坍塌事故多次发生，给正常施工带来较大影响。盾构隧道开挖面稳定性研究的关键在于支护力的确定，工程实践更关注维持开挖面稳定所需要的最小支护力，即极限支护力。开挖面附近土体可分为松动破坏区和土拱区[1]，如图1所示，极限支护力的确定与开挖面上方土拱效应密切相关[2]。由于土拱区的存在，松动破坏区受到上方土体压力小于上覆土体自重，在极限支护力计算时需考虑土拱效应的影响。

图1 开挖面失稳变形分区示意

众多学者对盾构开挖面稳定性进行过试验研究。ATKINSON 等[3]利用离心机研究密砂中二维盾构开挖面稳定性问题。CHAMBON等[4]进行干砂开挖面稳定性离心试验，得到开挖面支护力与位移关系曲线及地表横断面沉降曲线。MAIR等[5]进行关于盾构的一系列离心试验，研究饱和软土开挖面稳定性问题。KAMATA等[6]采用离心试验方法研究砂土开挖面超前导管的支护作用。但上述研究均未对开挖面上方应力变化引起的土拱效应进行分析，鉴于此，陈仁朋等[1]在模型试验中监测开挖面附近土压力的变化，并根据试验结果将开挖面前方土体的变形归纳为不同分区，包括土拱区、松动破坏区、整体失稳破坏区等，如图1所示。

开挖面支护力减小导致开挖面前方土体应力重分布，引起的土拱效应对开挖面稳定性及地表沉降产生重要影响，对开挖面上方的土拱效应需进行深入分析。地下水存在会对土拱效应产生明显影响。对于砂土地层，地下水的存在由于浮力作用降低了砂土的“视重”，并且会改变砂土内摩擦角，因此将对开挖面上方的土拱产生影响，进而影响开挖面最小支护力的大小。

因此，本文针对水土耦合作用对开挖面上方土拱效应的影响进行综合分析，研究地下水对土拱高度的影响原理，并结合楔形体模型分析地下水对开挖面最小支护力的影响。

1 地下水对土拱高度影响的试验结果

1.1 模型试验方法

针对干砂情况下土拱对开挖面所需最小支护力的影响，KIRSCH[7]在常重力情况下进行模型试验。IDINGER等[8]采用离心机进行模型试验。陈仁朋等[1]采用直径为1 m的盾构模型进行常重力下大尺寸模型试验研究。本文主要分析地下水对开挖面上方土拱效应的影响，参考KIRSCH的试验方法，设计如图2所示的试验系统，在常重力下进行模型试验。试验系统由玻璃模型槽、隧道装置以及照相系统组成，通过透明的玻璃模型槽对隧道装置附近砂土进行照相，再通过数字照相量测软件分析开挖面前方砂土位移[9]，研究土拱高度变化规律。

图2 模型试验示意

1.2 地下水对开挖面上方土拱高度的影响

土拱效应的产生原因是砂土之间存在相对位移[10]。本文主要分析地下水的存在对开挖面上方土拱高度的影响，因此设定土拱边界的判断标准为：砂土位移大于1 mm和小于1 mm的分界线。由此得到不同情况下的土拱高度见表1，表1中土拱高度减小比例η的计算见式( 1 )。

( 1 )

表1 不同埋深时地下水对土拱高度影响的试验结果

说明：本表为开挖面位移为3 mm时的结果。

根据表1试验结果可知，地下水的存在可减小开挖面上方土拱高度，在相同的开挖面情况下，地下水使土拱高度减小的比例为10%～15%。

2 地下水对开挖面土拱效应影响数值计算分析

2.1 数值计算模型

为分析地下水对土拱高度的影响原理，本文进行数值分析。根据工程实际情况，建立尺寸为80 m×50 m×51 m的计算模型，隧道直径为6 m，模型共包含38 125个单元，共40 570个节点，计算模型如图3所示。采用分步开挖的计算方法，每步开挖长度为1.2 m。隧道开挖至模型一半长度位置处，即25 m。隧道开挖面支护力取0.6倍侧土压力。模型的左右和前后边界为水平位移约束，底部为垂直位移约束，顶部为自由面。当隧道开挖至模型中部时，逐渐减小开挖面支护力，依次取值为0.5倍、0.4倍、0.3倍侧土压力，由此与模型试验相对应，分析支护力逐渐减小过程中开挖面土体的位移情况。

图3 数值计算模型示意

根据相关试验研究，地下水的存在将减小砂土内摩擦角。在数值计算中，通过减小砂土的内摩擦角来体现地下水的影响。

2.2 不同砂土内摩擦角对土拱高度的影响

在数值计算中，土拱高度的确定与模型试验类似，为砂土位移超过10 mm的最高点到隧道拱顶的垂直距离(图4)。为便于分析，将此土拱高度与隧道直径的比值定义为相对土拱高度，不同内摩擦角情况下相对土拱高度的计算结果如图5所示。根据图5可知，砂土摩擦角的改变，将影响开挖面附近砂土的位移，进而影响砂土的应力传递过程，最终使土拱的高度和形状发生改变。数值计算结果说明，地下水对土拱高度产生影响的原因是砂土内摩擦角的变化。

图4 内摩擦角为20°时的砂土位移云图

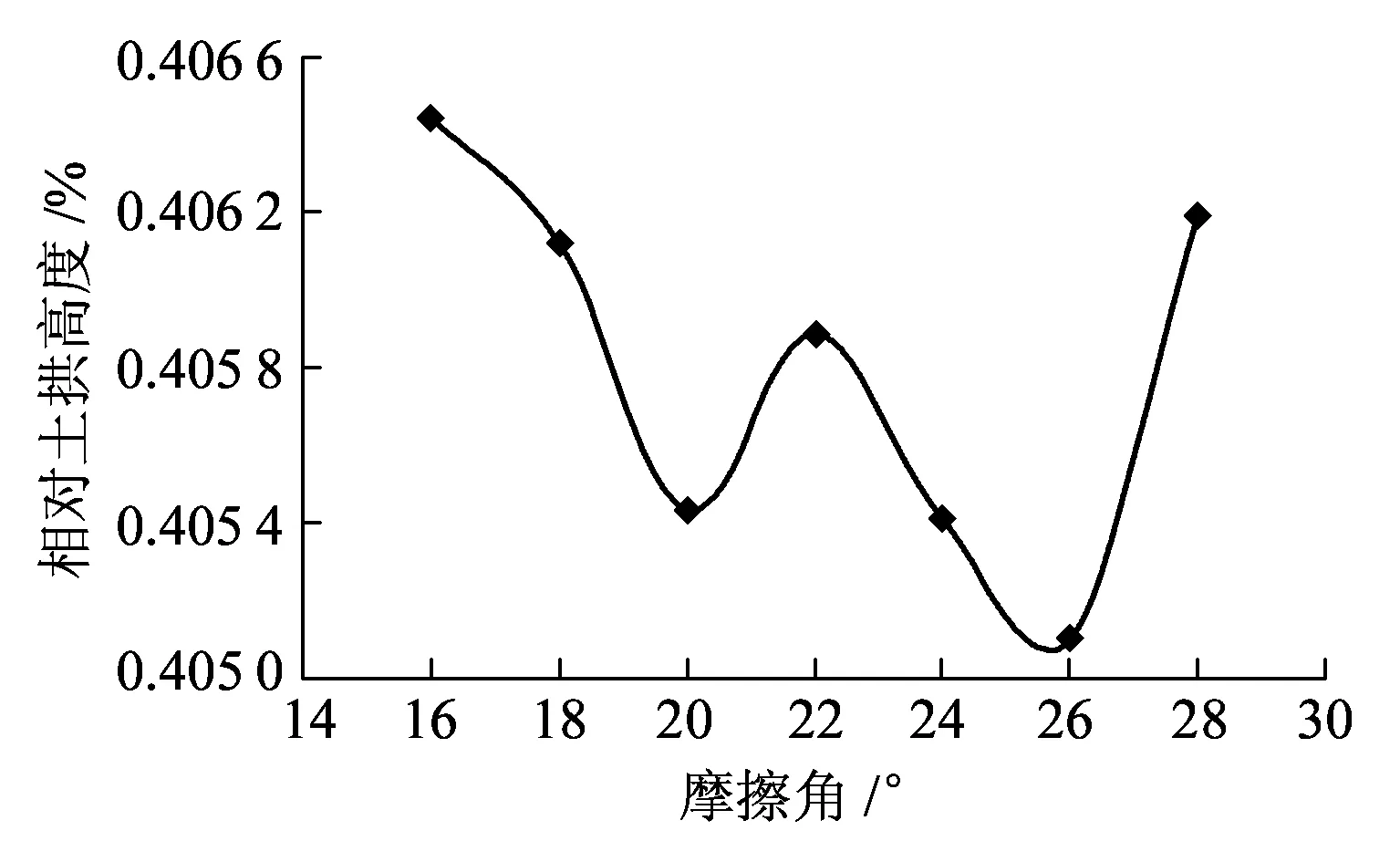
图5 不同砂土内摩擦角对土拱高度系数的影响曲线

3 砂土地层中开挖面最小支护力计算方法修正的讨论

对于开挖面最小支护力的理论研究，最早进行的是塑性极限分析法[11]，但由于塑性极限分析求解较繁琐，近年来相对简单的楔形体计算模型得到广泛应用[12]。基于Janseen的筒仓理论，得到三维楔型体模型[12]，它由一个位于掘进面前方的楔型体和掘进面上方的棱柱体两部分组成，如图6所示。在此基础上，JANCSECZ等[12]假设地层均匀，楔型体上方棱柱体考虑土体的松动土压力，由此计算开挖面的最小支护压力。文献[13-15]考虑到地下水渗流和分层土的影响，对模型进行改进。

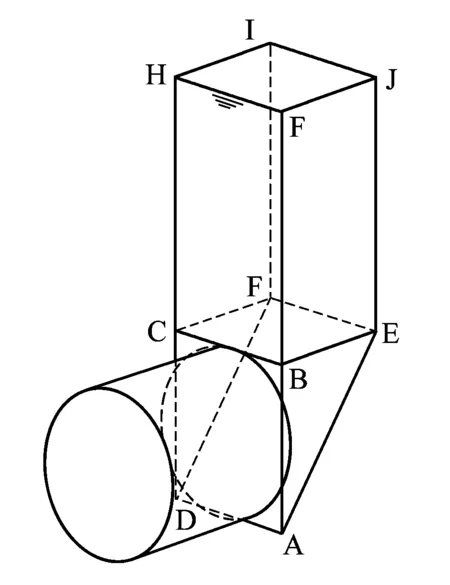
图6 楔形体分析模型示意

在楔形体计算模型中计算上方棱柱体对下方楔形体压力时，考虑的一个重要因素是开挖面上方的土拱效应[14]。相关文献的模型试验结果显示，楔形体上方部分土体荷载并未作用在楔形体上，而是由周围土体承担[14，16]。因此作用在楔形体上的荷载比上覆土体的总重小。在计算时一般通过棱柱体侧土压力系数来体现土拱效应的影响(图6)，进而体现土拱对开挖面稳定性的积极作用，不同学者给出不同的取值方法。文献[10]假设K为一经验常数，建议取值为1。文献[17]假设采用朗肯被动土压力系数。文献[18]分析了土拱区域土体的主应力方向旋转，给出修正侧压力系数。这些分析均未考虑地下水对开挖面上方土拱效应的影响。

3.1 楔形体上覆土压力的确定

在计算开挖面最小推力的楔形体模型中，计算上方棱柱体对下方楔形体的土压力是难点[10]。其中需要考虑的关键因素为开挖面上方的土拱效应，目前对于土拱高度的计算还没有较合适的方法。常用的分析方法为太沙基松动土压力理论[10]，该理论认为在上部土体中沿开挖面两侧形成了剪切面，下部土体受到的压力为土体自重减去剪切面上受到的滑动阻力。太沙基松动土压力理论考虑了隧道尺寸、埋深、土体力学参数等对土体稳定性的影响，因此本文采用太沙基松动土压力理论分析上覆土体压力。

图7 太沙基松动土压力计算模型示意

图7所示分析模型中侧土压力系数K的取值，与开挖面上方的土拱效应密切相关。根据文献[16]的研究，在不考虑地下水对土拱效应影响时K取值为静止侧土压力系数，即K=K0=1-sinφ。

(1)隧道埋深较小时

根据试验结果，当隧道埋深为D时，开挖面前方滑动面发展到地表，此时开挖面需要支护的土体为整个滑动面上方土体，如图8所示，此时不考虑土拱的影响。直接采用ANAGNOSTOU的楔形体模型进行计算即可[13]，有地下水和无地下水时的计算方法相同。

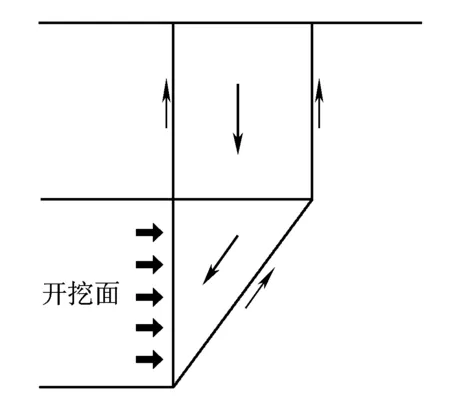
图8 隧道埋深为D时开挖面最小支护力计算示意

(2)隧道埋深较大时

根据试验结果，当隧道埋深为2D和3D时，需考虑开挖面上方的土拱效应。前文模型试验结果显示，地下水的存在降低了土拱高度，因此，在有地下水的情况下对侧土压力系数进行修正，修正系数设为kw。根据模型试验结果，给出式( 2 )所示修正系数kw的建议值。

需要说明的是，式( 2 )为根据实验结果给出的kw建议取值，对此取值的验证需进行进一步试验(包括土压力监测)。根据本文试验结果，可以得知当H/D>1时，kw<1。因此，在式( 2 )中，kw取0.9，式中H为隧道埋深。

( 2 )

如图5所示，厚度为dh土条的平衡方程为

( 3 )

( 4 )

( 5 )

其中土条宽度为

式中：R为隧道半径；φ为土体内摩擦角。

3.2 隧道开挖面最小支护力的计算

(1)水土分算说明

采用水土分算方法计算开挖面最小支护力F，即开挖面所需支护力分为两部分，对土的有效支护力和水压力，如式( 6 )所示。

F=Pw+P′

( 6 )

式中：Pw为开挖面受到的水压力，在本文分析中，假设开挖面为不透水边界，即不考虑开挖面地下水渗流的影响，因此Pw为静水压力，即Pw=γw×(C+D/2)；P′为根据楔形体模型计算出的开挖面所需最小有效支护力，计算方法见下文。

需要注意的是，对于干砂与饱和砂的计算，在滑动面上需采用不同的计算参数，对于饱和砂需采用其浮重度γ′和有效内摩擦角φ′。

(2)开挖面最小支护力的计算方法

通过分析滑动面前方楔形体的平衡(图9)来确定极限支护压力。

图9 作用在楔形体上的力

滑动面上各点的抗剪强度为

τ=c′/v+σ′tanφ′/v

( 7 )

式中：c′为有效内聚力；φ′为有效内摩擦角；v为安全系数。

楔形体水平力的平衡：

2T′cosα+P+(C+Ntanφ)·cosα=Nsinα

楔形体竖向力平衡：

Pv+W=(C+Ntanφ)sinα+Ncosα+2T′sinα

以上两式进行变换消去N得

(tanφsinα+cosα)+2T′sinα

最终可求解极限有效支护压力P′计算公式为

( 8 )

其中：

因此最终需要的开挖面最小支护力为

F=Pw+P′=

( 9 )

其中T′的计算需考虑到地下水对开挖面上方土拱的影响。

通过不同楔形体角度α的试算即可确定开挖面所需最小支护力。

3.3 干砂与饱和砂最小支护力计算结果对比分析

根据上文得到的方法，计算不同参数对开挖面最小支护力计算结果的影响。

(1)埋深的影响

不同埋深情况下的计算结果如图10所示。当隧道埋深较浅(D)时，开挖面前方滑动面滑动到地表，未考虑地下水对土拱效应的影响，同时由于水压力的作用，饱和砂得到的计算结果较干砂大。当隧道埋深较大时(3D)，由于通过修正系数kw考虑了地下水对开挖面上方土拱效应的影响，减小了饱和砂需要的最小支护力，因此饱和砂与干砂最小支护力的差值减小。

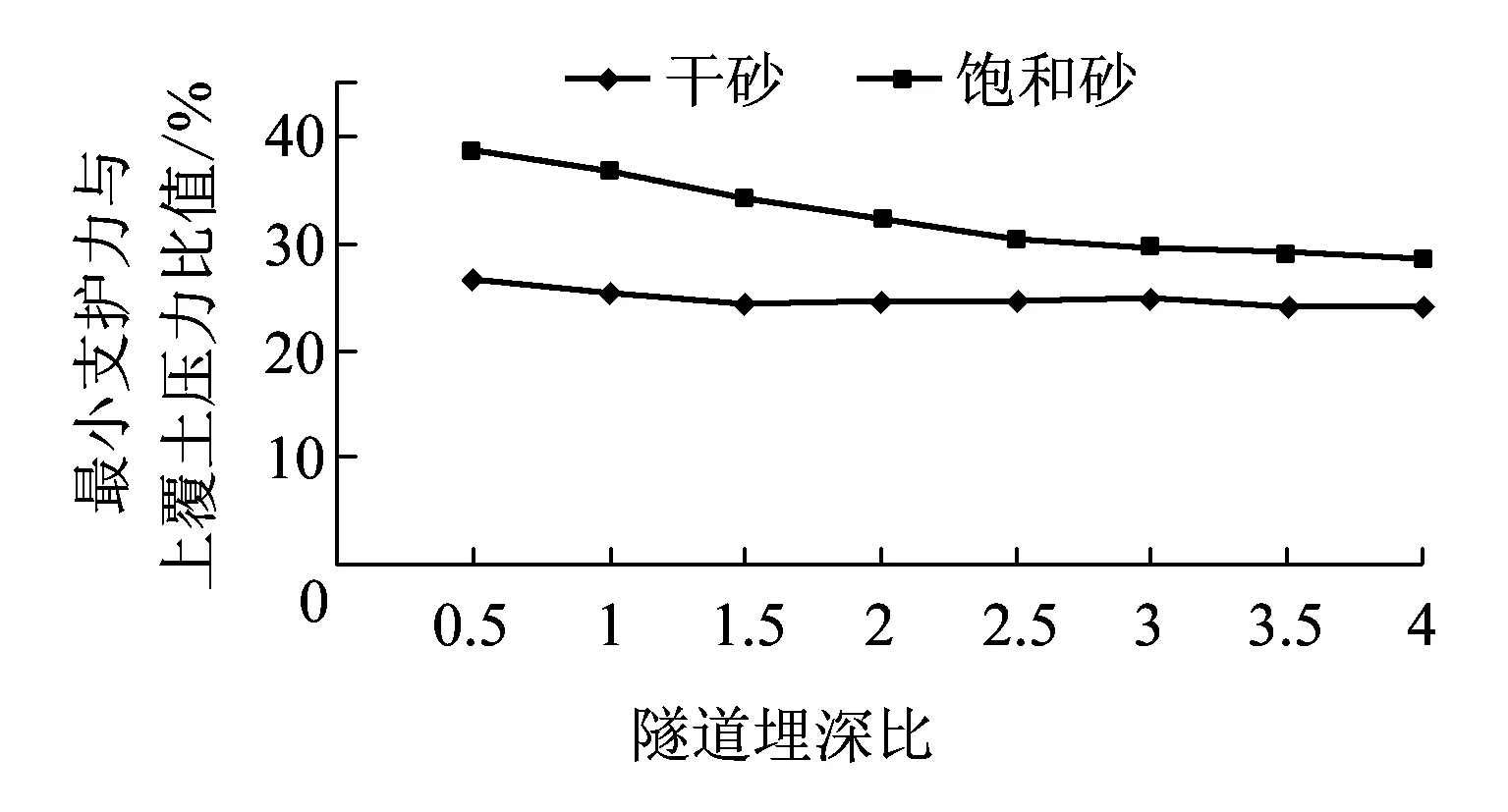
图10 不同埋深情况下开挖面最小支护力计算结果

(2)修正系数kw对计算结果的影响

不同修正系数情况下的计算结果如图11所示。由图11可知，修正系数的取值对开挖面最小支护力的影响明显，当修正系数取值为2时，最小支护力减小16.5%。由此说明，地下水的存在降低了最小支护力与上覆土压力的比值，修正系数的物理意义为考虑地下水对开挖面上方土拱形成的有利作用，因此在计算开挖面最小支护力时需考虑地下水对土拱效应的影响。

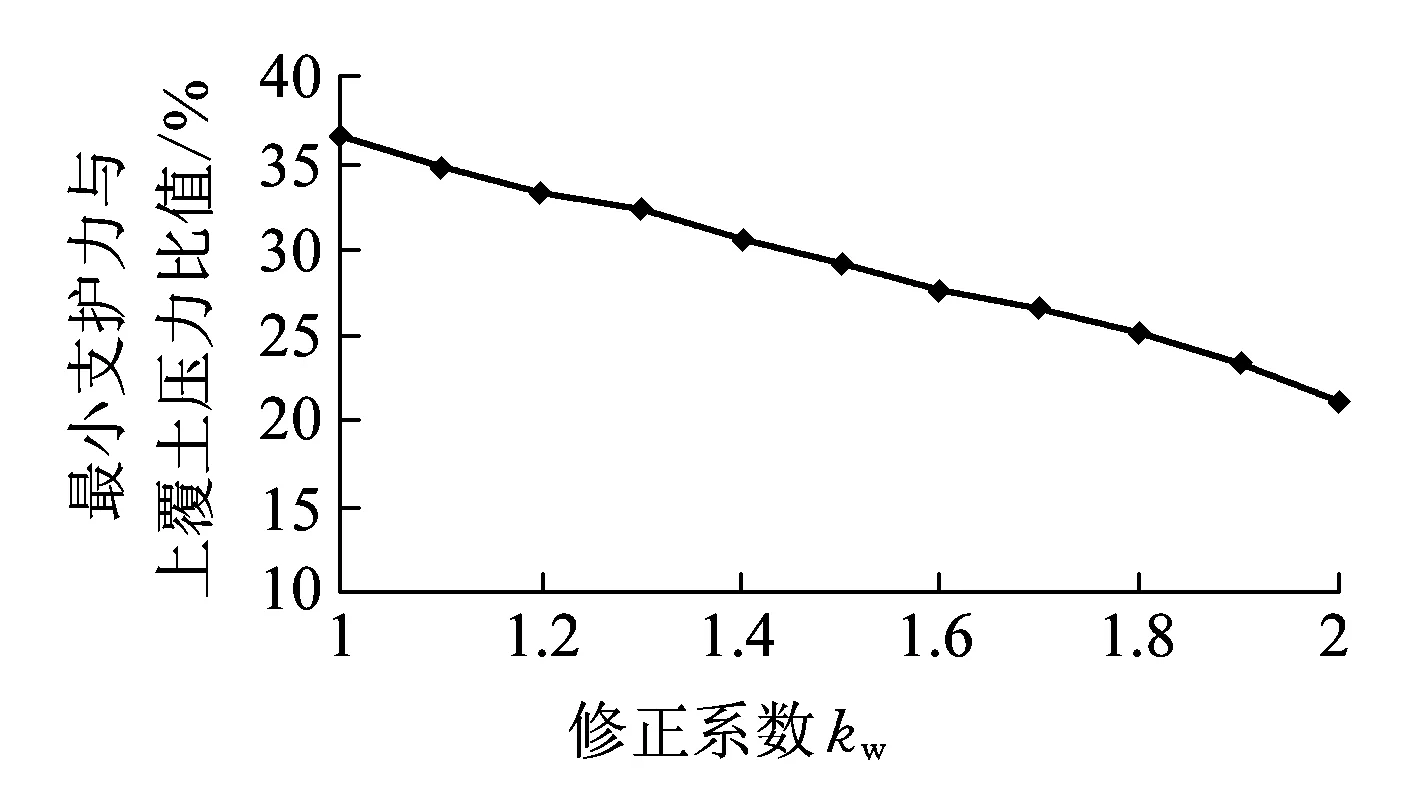
图11 修正系数kw取值对开挖面最小支护力计算结果的影响(C/D=2)

(3)干砂与饱和砂不同内摩擦角取值对计算结果的影响

相同砂土在饱和状态时的力学参数与干燥状态的力学参数不同，通常情况下饱和砂的内摩擦角比干砂小，在模型试验中砂土摩擦角的测量结果即为如此，见表2。为分析此现象对开挖面最小支护力计算结果的影响，特设定饱和砂内摩擦角与干砂内摩擦角的不同比值(即图12中横坐标所示饱和砂内摩擦角降低系数)，分析此比值对计算结果的影响，并绘制于图12中。

表2 砂土内摩擦角测试结果

图12 饱和砂内摩擦角降低系数对最小支护力的影响

计算结果显示，饱和砂内摩擦角的降低可明显增大最小支护力的计算结果，因此在计算开挖面支护力时需采用饱和砂的力学参数；仍采用干砂的力学参数将降低开挖面安全系数。

4 结论

本文针对水土耦合对盾构隧道开挖面上方土拱效应的影响进行综合分析，得到如下结论：

(1)试验结果显示地下水的存在会减小土拱的发展高度；在相同开挖面位移时，相对于干砂情况地下水减小土拱高度的比例为10%～15%。

(2)在三维数值计算中，通过砂土内摩擦角的变化体现地下水的影响。由计算结果可知，内摩擦角的变化会影响土拱高度，说明地下水对土拱高度的影响是通过砂土内摩擦角的变化体现的。

(3)由于地下水的存在降低了砂土地层中的土拱高度，本文结合楔形体模型提出针对土拱效应的计算修正系数kw，即对上方棱柱体受到的侧土压力系数进行修正来体现地下水对开挖面上方土拱效应的影响。

(4)分析结果显示，地下水的存在降低了最小支护力与上覆土压力的比值，有利于土体稳定；在最小支护力计算中需采用饱和砂土的有效内摩擦角，否则将降低开挖面安全系数。

参考文献：

[1]陈仁朋，李君，陈云敏,等.干砂盾构开挖面稳定性模型试验研究[J].岩土工程学报，2011,33(1)：117-122.

CHEN Ren-peng, LI Jun,CHEN Yun-min,et al.Large-scale Tests on Face Stability of Shield Tunnelling in Dry Cohesionless Soil[J].Chinese Journal of Geotechnical Engineering,2011,33(1):117-122.

[2]武军，廖少明，时振昊.考虑土拱效应的盾构隧道开挖面稳定性[J].同济大学学报，2015，43(2)：213-220.

WU Jun,LIAO Shao-ming,SHI Zhen-hao.Work Face Stability of Shield Tunnel Considering Arching Effect[J].Journal of Tongji University,2015,43(2)：213-220.

[3]ATKINSON J H,POTTS D M.Stability of a Shallow Circular Tunnel in Cohesionless Soil[J].Geotechnique,1997,27(2):203-215.

[4]CHAMBON P,CORTE J F.Shallow Tunnels in Cohesionless Soil:Stability of Tunnel Face[J].Journal of Geotechnical Engineering,1994,120(7):1148-1165.

[5]MAIR R J,TAYLOR R N.Theme Lecture:Bored Tunnelling in the Urban Environment[C]// Proceedings of the 14th International Conference on Soil Mechanics and Foundation Engineering,Hamburg,1997:2353-2385.

[6]KAMATA H,MASIMO H.Centrifuge Model Test of Tunnel Face Reinforcement by Bolting[J].Tunnnelling and Underground Space Technology,2003,18(2-3):205-212.

[7]KIRSCH A.Experimental Investigation of Face Stability of Shallow Tunnels in Sand[J].Acta Geotechnica,2010,(5)：110-116.

[8]IDINGER G,AKLIK P,WU W,et al.Centrifuge Model Test on the Face Stability of Shallow Tunnel[J].Acta Geotechnica,2011,6(2):105-117.

[9]李元海，靖洪文，朱合华,等.数字照相量测在砂土地基离心试验中的应用[J].岩土工程学报，2006,28(3)：306-311.

LI Yuan-hai,JING Hong-wen,ZHU He-hua,et al.Experimental Investigation on Progressive Deformation Patterns of Sand Foundation in Centrifuge Test Using Digital Photogrammetry[J].Chinese Journal of Geotechnical Engineering,2006,28(3)：306-311.

[10]TERZAGHI K.Theoretical Soil Mechanics[M].New York:John Wiley and Sons,1943:37-42.

[11]LECA E,DOMIEUX L.Upper and Lower Bound Solutions for the Face Stability of Shallow Circular Tunnels in Frictional Material[J].Geotechnique,1990,40(4):581-606.

[12]JANCSECZ S,STEINER W.Face Support for a Large Mix-shield in Heterogeneous Ground Conditions[C]//Tunnelling 94,London,1994:531-550.

[13]ANAGNOSTOU G,KOVARI K.Face Stability Conditions with Earth-pressure-balanced Shields[J].Tunnelling and Underground Space Technology,1996,11(2):165-173.

[14]BROERE W.Face Stability Calculation for a Slurry Shield in Heterogeneous Soft Soils[C]//Proceedings of the World Tunnel Congress 98 on Tunnels and Metropolises.Sao Paolo,1998:215-218.

[15]LEE I M,NAM S W,AHN J H.Effect of Seepage Forces on Tunnel Face Stability[J].Canadian Geotechnical Journal,2003,40(2):342-350.

[16]BROERE W.Tunnel Face Stability & New CPT Applications[M].Netherlands:Delft University Press,2001:32-36.

[17]Anonymous.Interaction Between Backfill and Rock Mass in Narrow Stopes[J].Tikoubelem.uqat.ca,2003:1157-1164.

[18]HANDY R L.The Arch in Soil Arching[J].Journal of Geotechnical Engineering,ASCE,1985,111(3):302-318.