带悬臂板薄壁箱梁的扭转和畸变分析

徐 勋，叶华文，强士中

(西南交通大学 土木工程学院，四川 成都 610031)

改进和发展薄壁箱梁的扭转和畸变效应分析，一直是国内外学者的研究课题。经典的闭口薄壁杆件扭转和畸变理论建立在不带悬臂板基础上，而目前箱形桥梁几乎都带有悬臂板，尤其是公路混凝土箱梁和组合箱梁，其悬臂板占整个顶板较大比例[1，2]，因此经典理论需进一步改进和发展才能适用于目前的箱梁结构。

薄壁杆件扭转分析的通用理论只涉及纯开口截面[3]或纯闭口截面[4]，这两种理论从基本假设到最终结果均有差别[5]。文献[6，7]将开口和闭口薄壁梁扭转理论统一在乌曼斯基假定下，建立开口和闭口薄壁梁扭转的统一基本微分方程。文献[8，9]将薄壁截面中线用多边形近似拟合，推导出一种开口和闭口薄壁梁的扭转理论，其最终的微分方程组较复杂，没有解析解。文献[10]对悬臂板在薄壁箱形梁扭转中的作用进行研究，但未对畸变效应进行分析。薄壁箱梁畸变分析的通用理论只涉及纯闭口截面[11，12]。文献[13，14]建立了任意截面薄壁梁的畸变分析方法。已有研究很少就悬臂板在薄壁箱梁中的抗扭和抗畸变作用问题进行分析，但悬臂板是薄壁箱梁扭转和畸变的控制构件。

对此，本文基于广义坐标法，建立带悬臂板薄壁箱梁扭转、畸变的位移模式和几何方程，采用混合变分原理，建立新的开闭口混合截面杆件扭转和畸变分析理论。由于该理论以位移和应力作为变分参量，可以充分考虑剪切效应。基于该理论，分析薄壁箱梁剪力流的分布和组成，比较统一了剪力流的两种计算方法。在对悬臂板内力状态分析基础上，研究悬臂板对整个截面剪切变形的影响及对整个截面抗扭和抗畸变的贡献。

1 基本方程

以图1中带4悬臂板的对称薄壁梯形箱梁为分析对象。在分析薄壁箱梁扭转和畸变效应时，作如下假设：①悬臂板在其根部与闭口部分刚性连接；②开口和闭口部分具有同样的扭转翘曲函数和畸变翘曲函数；③忽略壁板厚度对翘曲的影响；④箱梁各壁板沿板平面切向不可伸缩；⑤忽略扭转翘曲和畸变翘曲的耦联效应[14]。

注：O、S、N分别为截面形心、扭转中心、畸变中心。

图1 典型截面

图2 坐标系和积分路径

基于图2所规定的坐标系和位移方向，箱壁中面上任一点的纵向位移uz(s，z)、周向位移us(s，z)及法向位移un(s，z)分别为

(1a)

(1b)

(1c)

翘曲位移模式由∂uz/∂s+∂us/∂z=q/(Gt)得到。

(2a)

(2b)

其中

(3a)

(3b)

图3 截面位移

(4a)

(4b)

(4c)

式中：n为箱壁任一点M1的法向坐标。

箱壁应变由几何方程确定。

(5a)

(5b)

(5c)

基于式( 5 )，由胡克定律得出扭转翘曲正应力σw、畸变翘曲正应力σd和畸变横向弯曲应力σs为

σz=σw+σd=E1εz，σs=E1εs

( 6 )

引入扭转和畸变双力矩Bw、Bd及畸变剪力Qd

(7a)

(7b)

(7c)

从而可得

( 8 )

2 剪应力分析

由微元纵向平衡条件∂(σzt)/∂z+∂(τzst)/∂s=0得

( 9 )

式中：(τzst)0为待定剪力流，记为q(0，z)。

剪力流q(s，z)可分解成扭转剪力流qw(s，z)和畸变剪力流qd(s，z)。将式( 5 )、式( 6 )代入式( 9 )，考虑到各分支悬臂板外端点ID0i剪力流q(0，z)为零，可得i分支悬臂板剪力流为

(10)

其中

(11)

可以看出，qi(s，z)的值与主扇形零点的位置无关。

对于闭口区段，考虑到有来自i分支悬臂板内端点IDi的剪力流qi(si，z)参与平衡，并设闭口区段上s在点IDi和IDi+1之间，可得闭口区段上剪力流为

(12)

式中：q(0，z)为主扇形零点待定的超静定剪力流。

将式( 5 )、式( 6 )和式(10)代入式(12)可得

(13)

式中

(14)

将超静定剪力流q(0，z)分解成扭转剪力流qw(0，z)和畸变剪力流qd(0，z)。文献[15-18]中，关于超静定剪力流q(0，z)计算有两种方法：对于扭转剪力流qw(0，z)，第一种方法按照qw(0，z)使整个截面的扭转剪力流满足扭矩平衡求得；第二种方法按照qw(0，z)满足闭口位移连续条件求得。对于畸变剪力流qd(0，z)，第一种方法按照qd(0，z)使整个截面的畸变剪力流对扭转中心不形成扭矩求得；第二种方法按照qd(0，z)满足闭口位移连续条件求得。下面就两种计算方法进行对比分析。

2.1 第一种方法

第一种方法可表示为

(15a)

(15b)

(16a)

(16b)

则箱梁截面的开口部分或闭口部分上任意s处剪力流可表示为

(17)

(18a)

(18b)

(19a)

(19b)

2.2 第二种方法

第二种方法可表示为

(20a)

(20b)

将式(10)、式(13)代入式(15)可得

(21a)

(21b)

箱梁截面的开口部分或闭口部分上任意s处剪力流可表示为

(22)

(23)

(24a)

(24b)

2.3 对比分析

(25)

分析可知，箱梁截面的剪力流由4部分组成，如表1 和图4所示：①平衡闭口部分翘曲正应力的剪力流，表示为qw1和qd1；②平衡开口分支悬臂板翘曲正应力的剪力流，即从分支悬臂板流入的剪力流，表示为qw2和qd2；③扭转剪力流是使第一部分剪力流满足截面的扭矩平衡或满足闭口连续条件的剪力流，畸变剪力流是使第一部分剪力流满足闭口连续条件的剪力流，表示为qw3和qd3；④扭转剪力流是使第二部分剪力流满足截面的扭矩平衡或满足闭口连续条件的剪力流，畸变剪力流是使第二部分剪力流满足闭口连续条件的剪力流，表示为qw4和qd4。如果不考虑分支悬臂板的贡献，第二、四部分剪力流将消失。

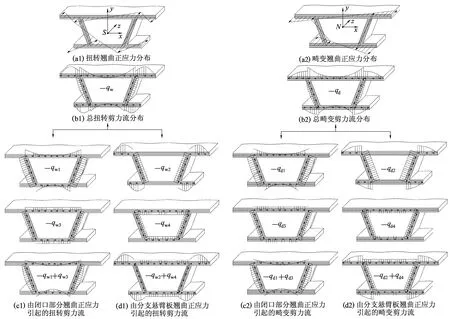
图4 截面剪力流分布

qw计算式qd计算式qw1-MwIθwwSθw(s)[]cqd1-MdIχwwSχw(s)[]cqw2-MwIθww∑im=1Sθw(si)[]iqd2-MdIχww∑im=1Sχw(si)[]iqw3MwIθww·∮Sθw(s)[]ctds∮1tdsqd3MdIχww·∮Sχw(s)[]ctds∮1tdsqw4MwIθww·∮∑im=1Sθw(si)[]i{}tds∮1tdsqd4MdIχww·∮∑im=1Sχw(si)[]i{}tds∮1tds

3 考虑剪切变形的控制微分方程

基于混合变分原理[19]，广义泛函为

(26)

式中：∏H-R(σ，u)为两个独立变分参量σ(应力向量)和u(位移向量)的能量泛函；ε(u)为应变向量；V*(σ)为余能密度；F为体力向量，此处为零；T为面力向量。

(27)

将式( 5 )代入式(27)整理得

(28)

余能函数为

(29)

将式( 8 )和式(22)代入式(29)整理得

(30)

反映剪切变形影响的剪切系数为

(31a)

(31b)

外荷载势能为

(32)

将式(28)、式(30)和式(32)代入式(26)变分可得

(33)

式(33)广义泛函变分的约束条件可写为：

①力的平衡方程

(34)

(35)

②力与位移的关系式

(36)

(37)

③控制微分方程

将式(36)代入式(34)得截面扭矩平衡方程

(38)

(39)

由式(38)和式(39)联立得到控制微分方程

(40)

在上述分析基础上，将控制微分方程式(40)中与悬臂有关的系数项取为0后，即与无悬臂箱梁的控制微分方程完全一致。微分方程(40)可采用初参数法[3]求解。

4 数值算例

4.1 算例1

以桥梁工程中典型的双悬臂对称薄壁矩形截面直线箱梁为研究对象，如图5所示。为分析悬臂板对结构扭转效应的影响，分别计算两种高宽比的模型：模型M1的高宽比h/b=0.5，b=5 m，h=2.5 m；模型M2的高宽比h/b=2，b=2.5 m，h=5 m；箱梁各壁板厚度均为t=0.2 m。以两悬臂板宽度与顶板宽度的比值d/b作为参量进行系列计算。

图5 计算模型

图6 截面特性比值随d/b变化曲线

图7 翘曲程度比值随d/b变化曲线

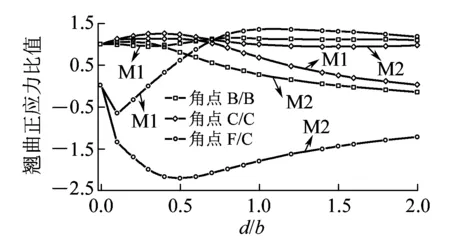
图8 翘曲正应力比值随d/b变化曲线

图9 翘曲系数比值随d/b变化曲线

对图6～图9曲线进行对比分析，得出如下结论：

(1)从图6可以看出，常规的双悬臂箱梁(d/b=0.5～1)，悬臂板的翘曲惯矩一般占全截面翘曲惯矩的30%～50%，即悬臂板分担了30%～50%约束扭矩，尤其是当闭口部分接近无翘曲截面[14](h/b渐近1)时，该比例将更大，因此悬臂板对截面约束扭转效应的贡献不应忽略。

(2)根据图6中的扭心位置比值曲线可以发现，对于模型M1，在d/b=0～0.5时，随着悬臂板的增长，扭心反而向底板移动；对于模型M2，随着悬臂板的增长，扭心一直向顶板移动。

(3)从图7可以看出，悬臂板的存在使截面翘曲系数增大，一般情况下，增幅约20%～70%，这表明悬臂板使剪切变形的影响增大。悬臂板增长也使全截面的翘曲惯矩增大，导致截面(Uθ)″降低。

(4)从图8可以发现，悬臂板使闭口箱的翘曲正应力发生明显重分布，闭口部分翘曲正应力整体减小。悬臂板端点F的翘曲正应力比闭口部分大，可达闭口部分的1.2～2.5倍，因此悬臂板通常是整个截面翘曲正应力的控制构件。

(5)从图9可以看出，对于开闭混合截面，乌曼斯基第二理论所得结果比较保守，如常见的悬臂比例d/b=1，两种翘曲系数比值分别为1.499(模型M1)和1.784(模型M2)，是乌曼斯基第二理论未考虑悬臂板的次生剪应力影响所致，可见乌曼斯基理论不宜用于开闭混合截面。

4.2 算例2

图10 截面特性比值随d/b变化曲线

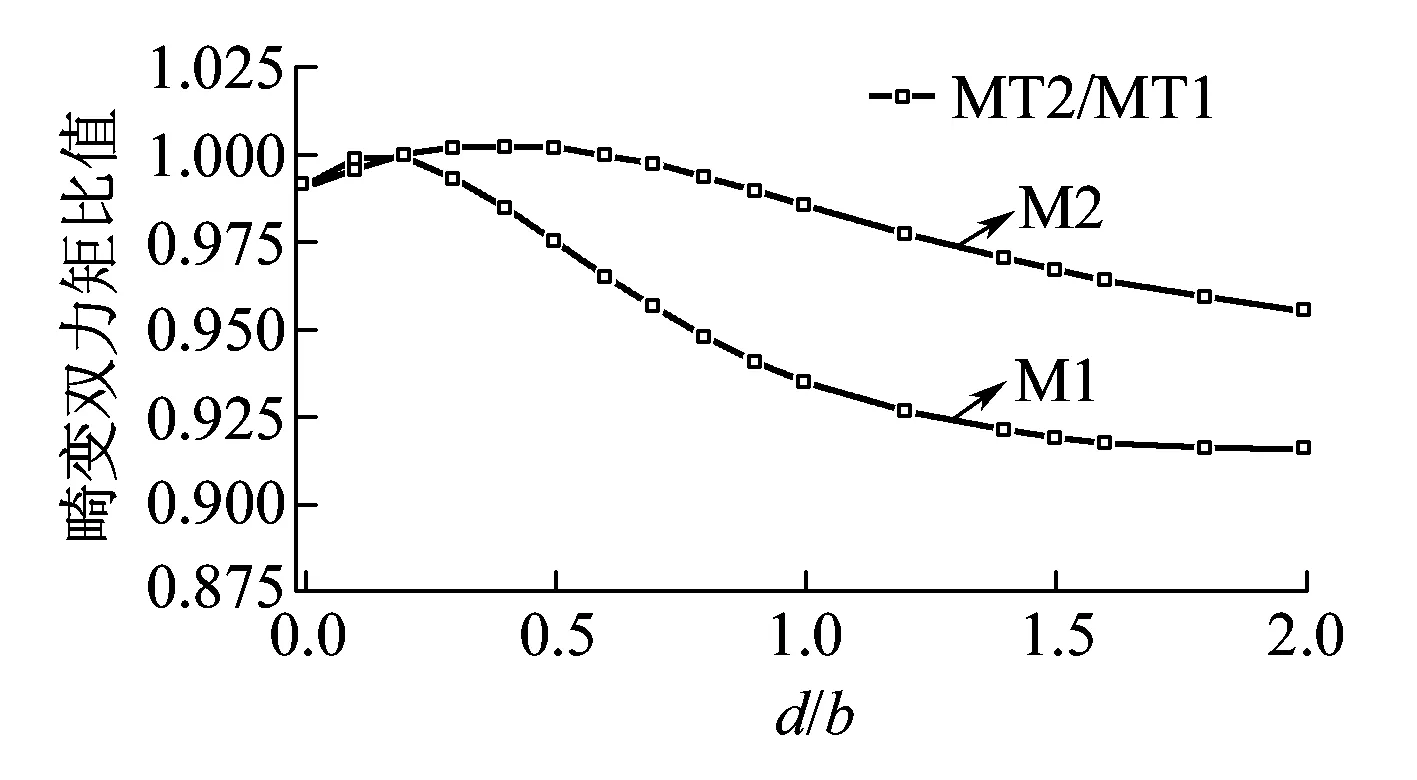
图11 畸变双力矩比值随d/b变化曲线

图12 翘曲正应力比值随d/b变化曲线

图13 剪切系数随d/b变化曲线

对图10～图13曲线进行对比分析，得出如下结论：

(1)从图10可以看出，对于常规双悬臂箱梁(d/b=0.5～1)，悬臂板的畸变惯矩通常占全截面畸变惯矩的30%以下，即悬臂板分担30%以下畸变力矩；悬臂板对截面畸变效应的贡献比对扭转效应的贡献小。

(2)从图10可以看出，随着悬臂板的增长，畸变中心位置始终向顶板移动，没有出现反复。

(3)从图11可以发现，悬臂板使闭口箱的畸变正应力发生明显重分布，随着悬臂翼缘板的增长，顶板角点B的畸变正应力逐渐减小，底板角点C的畸变正应力逐渐增大，底板角点C是整个截面畸变正应力的控制点。

(4)从图13可以看出，畸变剪切系数整体上均大于1，且悬臂板长度在一定范围时，该比值远超过1。但从图11可以发现，方法MT1、MT2所得畸变双力矩的相对误差在10%以下，这说明对于带悬臂板箱梁，次生剪应力对中面剪切变形的影响相对扭转效应要小得多。

5 结论

本文基于广义坐标法，建立带悬臂板薄壁箱梁扭转和畸变的位移模式与几何方程，采用混和变分原理，建立新的开闭口混合截面杆件扭转和畸变分析理论，得到如下结论：

(1)比较按照力矩平衡条件和闭口连续条件求解薄壁箱梁剪力流的两种方法，证明两种方法计算扭转剪力流结果一致，评价了两种方法计算畸变剪力流的合理性。

(2)分析薄壁箱梁剪力流的组成和分布，研究了悬臂板对整个截面扭转和畸变效应的影响及对整个截面剪切变形的影响。

(3)悬臂板对薄壁箱梁扭转和畸变效应的贡献主要体现在悬臂板扇形惯矩所占的比例；悬臂板使闭口箱翘曲应力发生明显的重分布；悬臂板使剪切变形影响增大，且这种影响随着悬臂翼缘板的增长而增大；常规薄壁箱梁桥中悬臂板的贡献不可忽略。

参考文献：

[1]任红伟.波纹钢腹板预应力混凝土箱梁弯曲性能试验研究[J].铁道学报,2008,30(1):60-64.

REN Hong-wei.Experimental Study on Prestressed Concrete Box-girders with Corrugated Steel Webs under Symmetrical Loads[J].Journal of the China Railway Society,2008,30(1):60-64.

[2]彭大文,颜海.曲线脊骨箱梁的剪力滞效应分析[J].铁道学报,2001,23(4):76-80.

PENG Da-wen,YAN Hai.Analysis of Shear Lag Effect in Curved Shine Box Girder[J].Journal of the China Railway Society,2001,23(4):76-80.

[3]VLASOV V Z.Thin-walled Elastic Beams[M].Washington,D.C.:National Science Foundation,1961.

[4]УМАНСКИЙ А А.Онормальных напряжениях лри кручении самолёга[J].Техника Воэлшного Флота,1940,(12):1-28.

[5]强士中,李乔.关于闭口薄壁杆件约束扭转的周边不变形理论[J].桥梁建设,1985,(1):63-75.

QIANG Shi-zhong,LI Qiao.Restraint Rigid-Torsion Theories of Thin-walled Girder with Closed Cross-Section[J].Bridge Construction,1985,(1):63-75.

[6]GUO Z H.A Unitied Theory of Thin-walled Elastic Structures[J].Journal of Structural Mechanical,1981,9(2):273-281.

[7]SHAKOURZADEH H,GUO Y Q,BATOZ J-L.A Torsion Bending Element for Thin-walled Beams with Open and Closed Cross Sections[J].Computers & Structures,1995,55(6):1045-1054.

[8]PROKIC A.Thin-walled Beams with Open and Closed Cross Sections[J].Computers & Structures,1993,47(6):1065-1070.

[9]PROKIC A.Computer Program for Determination of Geometrical Properties of Thin-walled Beams with Open-Closed Section[J].Computers & Structures,2000,74(6):705-715.

[10]周履.关于薄壁箱形梁的悬臂翼缘板在翘曲扭转中作用的探讨[J].世界桥梁,2003,(3):28-33.

ZHOU Lü.Exploration of Contribution of Cantilever Flanges of Thin-walled Box Girder to Its Behavior in Warping Torsion[J].World Bridges,2003,(3):28-33.

[11]WRIGHT R N,ABDEL-SAMAD S R,ROBINSON A R.BEF Analogy for Analysis of Box Girders[J].Jounal of the Structural Division,ASCE,1968,94(7):1719-1743.

[12]STEINLE A.Torsion und Profilverformung Beim Einzelligen Kastentraeger[J].Beton und Stahlhetonbau,1970,65(9):215-222.

[13]KIM J H,KIM Y Y.Analysis of Thin-walled Closed Beams with General Quadrilateral Cross Sections[J].Transportation of the Korean Society of Mechanical Engineerings A,ASME,1999,66(4):904-912.

[14]JONSSON J.Distortional Warping Functions and Shear Distributions in Thin-walled Beams[J].Thin-walled Structures,1999,33(4):245-268.

[15]RACHED E F.Non-uniform Warping Including the Effects of Torsion and Shear Forces.Part I:A General Beam Theory[J].International Journal of Solids and Structures,2007,44(18-19):5912-5929.

[16]平岛政治,臼木恒雄,廖庚甫,等.考虑剪切变形的任意四边形截面箱形梁畸变理论[J].世界桥梁,1980,(22):1-29.

PINDONG Zhen-zhi,JIUMU Heng-xiong,LIAO Geng-fu,et al.Distortion Theory of Box Girder with Arbitrary Quadrilateral Section Taking Account of Shear Deformation[J].World Bridges,1980,22(1):1-29.

[17]BOSWELL L F,LI Q.Consideration of the Relationships Between Torsion,Distortion and Warping of Thin-walled Beams[J].Thin-walled Structures,1995,21(2):147-161.

[18]ROBERT K D,TIMOTHY P J.Closed-form Shear Flow Solution For Box-girder Bridges under Torsion[J].Engineering Structures,2012,34:383-390.

[19]王勖成.有限单元法[M].北京:清华大学出版社,2003.