微纳卫星共面伴飞相对运动椭圆短半轴最省燃料控制

周美江 吴会英 齐金玲

(上海微小卫星工程中心,上海201203)

微纳卫星共面伴飞相对运动椭圆短半轴最省燃料控制

周美江 吴会英 齐金玲

(上海微小卫星工程中心,上海201203)

针对伴随微纳卫星资源受限、轨控需要尽可能节省燃料的现实问题,基于希尔(Hill)方程,研究推导了共面编队伴飞卫星的轨控时机和轨控方向对相对运动椭圆短半轴控制效率的影响。理论推导和仿真均表明:当控制量大小｜ΔV｜与相对运动椭圆短半轴b满足｜ΔV｜≤nb/2关系时(n为参考星平均轨道角速度),在相对运动椭圆上下点进行横向或反横向控制,最大效率地将相对运动椭圆短半轴改变了｜Δb｜=2｜ΔV｜/n。其中,在上点反横向或下点横向进行控制,可以最大效率地增大椭圆短半轴;在上点横向或下点反横向进行控制,可以最大效率地减小椭圆短半轴。

共面伴飞;希尔方程;椭圆短半轴;最省燃料控制;控制时机;控制方向;微纳卫星

1 引言

随着航天技术的不断发展和航天器应用水平的逐渐提高,多颗小卫星编队飞行协同开展航天任务已从概念验证转向实际应用。尤其是共面编队伴飞技术。由于在航天器故障诊断、空间目标立体成像等方面的巨大应用价值,该概念一提出就受到高度重视,以美国为代表的航天强国,更是将微纳卫星伴飞技术应用于空间目标监视和空间攻防对抗等领域[1-3]。

由于编队卫星功能的实现很大程度上依赖于编队构型,编队构型控制已成为编队卫星发展的关键技术之一。编队飞行的航天器间相对距离较近,可在相对运动框架下进行分析。常用的相对运动描述方法有两种[4]:一是基于两航天器轨道要素的运动学方法;二是基于两航天器相对位置速度状态的动力学方法,也称希尔(Hill)方程。运动学方法以两航天器的轨道要素为输入,适用范围广,外推精度高,目前很多编队构型控制以此为基础[5-6]。但由于轨道要素是随时间逐渐累积的慢变量,其抗扰动性能较差,对于有星间相对实时测量的编队构型控制问题,观测状态量需要进行转换,应用复杂。对于主星为圆轨道、相对距离较近的编队构型控制问题,将Hill方程进行线性化处理,可得到解析解。基于Hill方程解析解进行编队构型控制,模型物理含义清晰,相对观测量实时输入,计算量小,鲁棒性强,非常适用于有星间实时相对测量的星上自主编队构型控制问题。

对于共面编队伴飞构型控制来讲,相对运动椭圆短半轴的控制尤为重要。笔者所在团队前期基于微纳卫星只能进行横向或径向控制,对最高效率的相对运动椭圆短半轴控制时机进行了求解[7-8],本文将在前期工作的基础上,对共面编队伴飞构型控制中相对运动椭圆短半轴最省燃料控制的控制方向和控制时机进行系统求解,并用仿真去验证理论推导。

2 相对运动方程解

由Hill方程可知,伴随卫星在轨道面内相对参考星的相对运动解为相对轨道坐标系(x轴由地心指向参考星质心,为径向;y轴在轨道面内垂直于x轴沿飞行方向,为横向;z轴为轨道面法向)下长半轴为短半轴两倍的横向漂移椭圆,得到相对运动的几何解和参数解如下[9]:

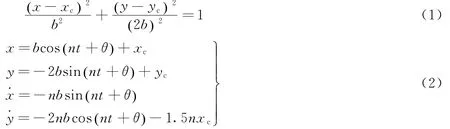
式中 n为参考星平均轨道角速度;(xc,yc)为相对运动椭圆中心;b为相对运动椭圆短半轴; Θ=nt+θ为伴随卫星在相对运动椭圆上的相位[10],θ为初始相位。

任一时刻t伴随卫星相对参考星在轨道面内相对状态分量(x,y,˙x,˙y) 已知,椭圆中心、椭圆短半轴和相位可写成:

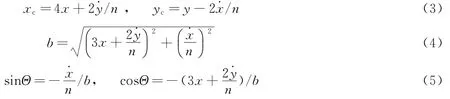
3 最省燃料控制问题的提出

推进系统消耗燃料转化为推力,一段时间内的推力作用使航天器动量(速度)改变,即燃料消耗相当于为航天器提供了一速度增量,所以最省燃料控制问题可等效为最小速度增量(也称控制量)控制问题。

将轨道面内的控制量ΔV分解为横向控制量ΔVy=ΔV cosφ和径向控制量ΔVx=ΔV sinφ(ΔV为控制量的大小;φ为控制方向角,从相对轨道坐标系的正y轴起算,逆时针旋转为正)。由式(4)可知,横向控制和径向控制均会改变椭圆短半轴。设横向控制量ΔVy与径向控制量ΔVx使椭圆短半轴改变Δb,由式(4)可知

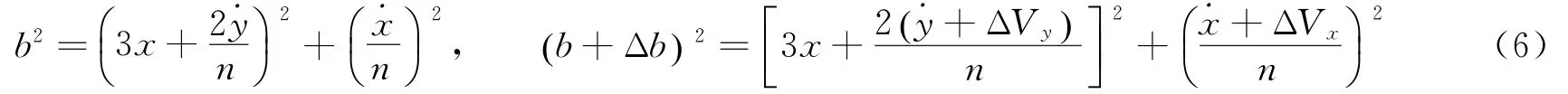
式(6)中两式相减并考虑式(2),可得

式(7)为Δb的一元二次方程,有两个数学解

引入中间变量

则式(8)可写为

由式(11)可知,控制量大小ΔV一定时,椭圆短半轴改变量Δb与控制时机Θ和控制方向φ相关。

微纳卫星资源和能源都严重受限,希望控制时尽可能节省燃料。对椭圆短半轴大小的控制来讲,即希望选择合适的控制方向和控制时机匹配,使控制量一定时控制效率最高(即ΔV一定时,求解使Δb最大的φ与Θ的匹配)。引入中间变量λ=ΔV/(nb)＞0,式(9)进一步化简为

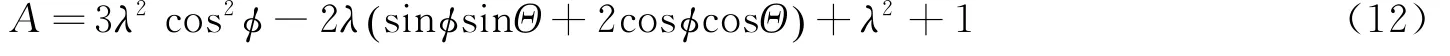
由式(12)可知,中间变量A为控制方向φ和控制时机Θ的二元连续函数,求其最大值。

A对控制时机Θ求一阶偏导数

A对控制方向φ求一阶偏导数

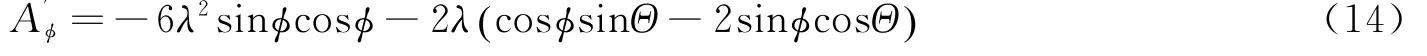
A对控制时机Θ求二阶偏导数

A对控制方向φ求二阶偏导数

A对控制时机Θ和控制方向φ求二阶混合偏导数,由于二阶混合偏导数连续,有

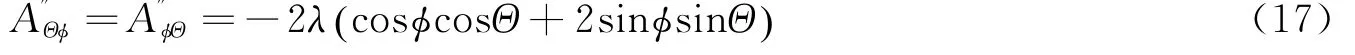
A取极值的必要条件之一为“一阶偏导数为0”,即

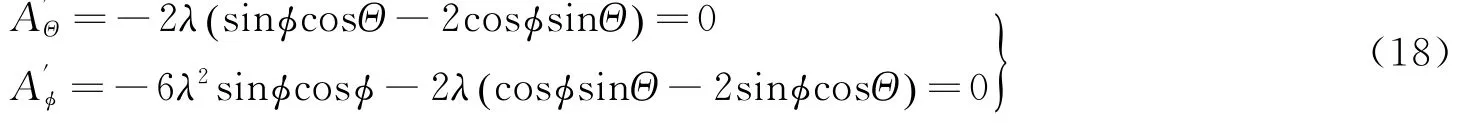
推得

4 最省燃料控制问题解的讨论

对式(19)的解分情况讨论如下。

4.1 cosΘ=0或cosφ=0

由式(18)可知,cosΘ=0与cosφ=0同时成立,即在左右点径向或反径向施加控制。

(1)Θ=90°,φ=90°(左点径向)或Θ=-90°,φ=-90°(右点反径向)

若A取极值,则必有

此时

当λ=1时,从物理意义上判定也为极值。即当λ≥1时,取极小值,此时椭圆短半轴改变量为

可能增大也可能减小椭圆。即在左点径向或右点反径向控制,当λ≥1,即ΔV≥nb时,考虑控制量从零逐渐加到ΔV,椭圆短半轴先减小到0后又增大,最终结果可能比初始椭圆短半轴小,也可能比初始椭圆短半轴大:

1)当1≤λ≤2,即nb≤ΔV≤2nb时,椭圆短半轴最终比初始椭圆短半轴小或等于初始椭圆短半轴;

2)当λ＞2,即ΔV＞2nb时,椭圆短半轴最终比初始椭圆短半轴大。

(2)Θ=90°,φ=-90°(左点反径向)或Θ=-90°,φ=90°(右点径向)

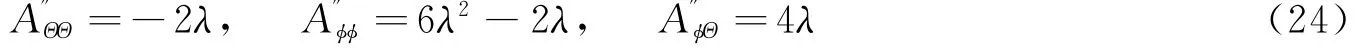
此时

恒成立,非极值,此时椭圆短半轴改变量为

肯定使椭圆短半轴增大。

4.2 cosΘ≠0且cosφ≠0(非左右点径向或反径向控制)

由式(19)可得

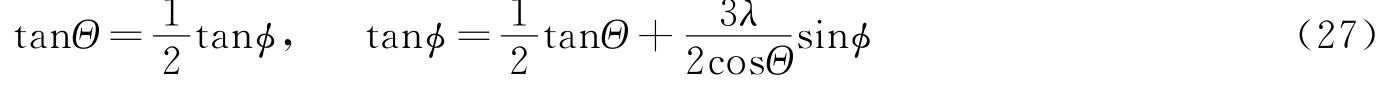
解算得到

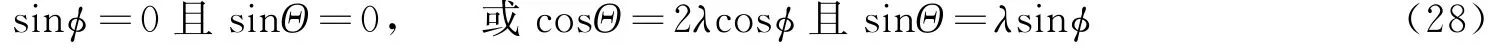
讨论两个解的情况如下。

(1)sinφ=0且sinΘ=0,即在上下点横向或反横向施加控制

1)φ=0°,Θ=0°(上点横向控制)或φ=180°,Θ=180°(下点反横向控制)时:

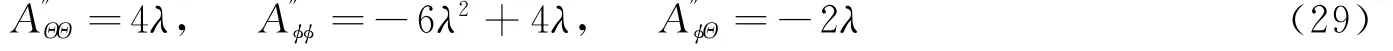
若A取极值,则必有

此时

当λ=1/2时,从物理意义上判定也为极值。即当λ≤1/2时,取极小值,此时椭圆短半轴改变量为

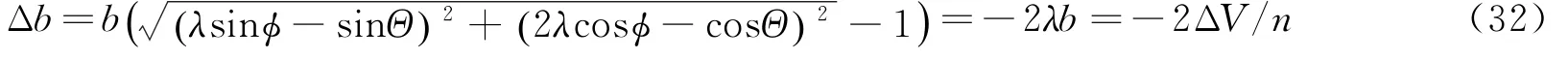
肯定减小椭圆。即当0＜λ≤1/2,0＜ΔV≤nb/2时,上点横向或下点反横向控制是极大效率减小椭圆的控制方向和控制时机匹配,此时椭圆短半轴减小2ΔV/n。

2)φ=180°,Θ=0°(上点反横向控制)或φ=0°,Θ=180°(下点横向控制)时:

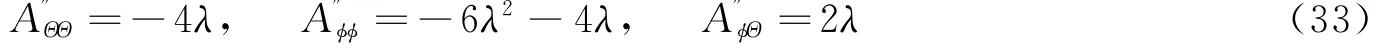
此时

恒成立,且

A取极大值。此时椭圆短半轴改变量为

肯定增大椭圆。即在上点反横向或下点横向控制时,极大效率地将椭圆短半轴增大2ΔV/n。

(2)cosΘ=2λcosφ且sinΘ=λsinφ

由式(2)可知,相对运动椭圆的矢径(起点为瞬时相对运动椭圆中心,终点为伴随卫星在椭圆上的位置)斜率为

控制量矢量斜率为

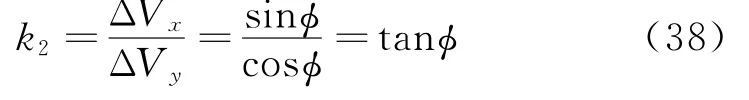
式(37)与式(38)相乘并考虑前提条件cosΘ=2λcosφ且sinΘ=λsinφ,得到

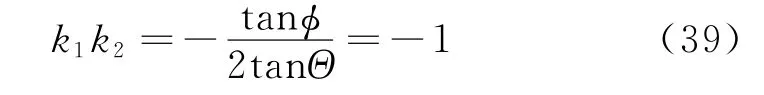
即控制方向垂直于矢径方向,且与相对运动方向成钝角,如图1所示,实线箭头表示矢径方向,虚线单箭头表示控制方向,虚线双箭头表示相对运动方向。

图1 控制方向垂直于矢径方向示意Fig.1 Control direction vertical to the radius vector

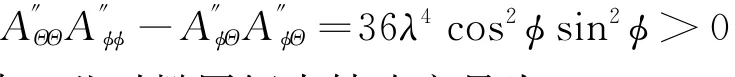
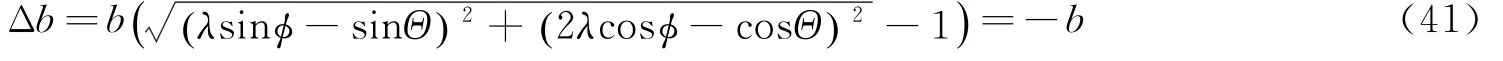
将椭圆减小为零。

由

得到1/2＜λ＜1,即当nb/2＜ΔV＜nb时,在任何时机,控制方向垂直于矢径方向进行控制(此时控制方向与相对运动方向成钝角),椭圆短半轴减小为零。控制量ΔV的大小即λ的值,由具体的控制时机Θ或控制方向φ按公式cosΘ=2λcosφ及sinΘ=λsinφ进行求解。

此外,由λ2=1/4+(3/4)sin2Θ可知:

1)当sin2Θ→0时,Θ→0°或180°,在趋于相对椭圆上下点进行控制,λ→1/2极小值,即ΔV→nb/2;

2)当sin2Θ→1时,Θ→±90°,在趋于相对椭圆左右点进行控制,λ→1极大值,即ΔV→nb;

5 理论推导结论

对所有推导总结如下:

结论1 无论λ取何值,即ΔV=λnb取何值,在上点反横向控制,或在下点横向控制,都是最大效率增大椭圆短半轴的控制方式。

结论2 当0＜λ≤1/2,即0＜ΔV≤nb/2时,在上点横向控制,或在下点反横向控制,最大效率减小椭圆短半轴。

结论3 当1/2＜λ＜1,即nb/2＜ΔV＜nb时,在非上下左右点的其他控制时机,垂直于矢径方向(且满足控制方向与相对运动方向成钝角)进行控制,最大效率减小椭圆短半轴至0,此时,控制量与控制时机满足cosΘ=2λcosφ且sinΘ=λsinφ。

结论4 当λ≥1,即ΔV≥nb时,在左点径向控制,或在右点反径向控制:

1)当1≤λ≤2,即nb≤ΔV≤2nb时,若控制量从0逐渐加到ΔV,椭圆短半轴先减小到0后又增大,但椭圆短半轴最终比初始值小,属于极大浪费燃料减小椭圆的控制方式。

2)当λ＞2,即ΔV＞2nb时,若控制量从0逐渐加到ΔV,椭圆短半轴先减小到0后又增大,但椭圆短半轴最终比初始值大,属于极大浪费燃料增大椭圆的控制方式。

也就是说,最大效率增大椭圆短半轴的控制方向和控制时机匹配是一定的,最大效率减小椭圆短半轴的控制方向和控制时机匹配则与控制量的取值区间有关。

6 仿真验证

设置一组仿真算例:参考星O为500 km圆轨道,交点周期T=5 676.978 s,伴随卫星A相对参考星O共面伴飞,初始伴飞椭圆短半轴b=5 158.606 m。在二体模型下,利用STK导出A相对O的初始轨道数据,基于Hill方程,对A在不同控制时机施加大小一定、方向不同的控制量,用Matlab编程求解椭圆短半轴的变化量。

针对不同λ取值区间对应结论不同的情况,设置λ=0.25、λ=0.75、λ=1.5、λ=2.5四组算例,对应不同λ取值区间,得到椭圆短半轴改变量与控制方向和控制时机的三维曲面和对应的二维投影如图2～图17所示。

图2 λ=0.25时Δb与φ和Θ的关系Fig.2 Relationship betweenΔb and φ,Θwhileλ=0.25

图3 λ=0.25时Δb在φ和Θ平面内的投影Fig.3 Δb projection in control direction-control time plane whileλ=0.25

图4 λ=0.25时Δb与φ和Θ的关系(Δb和φ面内投影)Fig.4 Projection relationship betweenΔb andφ,Θ: inΔb-φplane whileλ=0.25

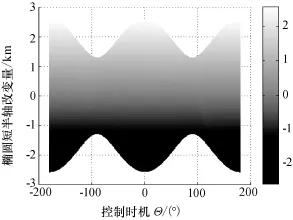
图5 λ=0.25时Δb与φ和Θ的关系(Δb和Θ面内投影)Fig.5 Projection relationship betweenΔb与φ,Θ: inΔb-Θplane whileλ=0.25

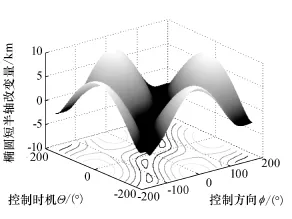
图6 λ=0.75时Δb与φ和Θ的关系Fig.6 Relationship betweenΔb and φ,Θwhileλ=0.75

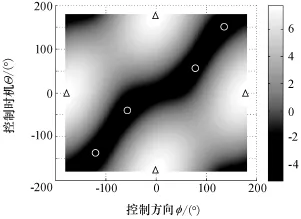
图7 λ=0.75时Δb在φ和Θ平面内的投影Fig.7 Δb projection in control direction-control time plane whileλ=0.75

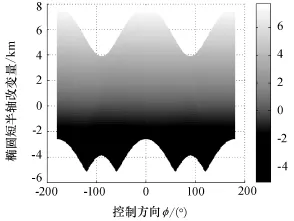
图8 λ=0.75时Δb与φ和Θ的关系(Δb和φ面内投影)Fig.8 Projection relationship betweenΔb andφ,Θ: inΔb-φplane whileλ=0.75

图9 λ=0.75时Δb与φ和Θ的关系(Δb和Θ面内投影)Fig.9 Projection relationship betweenΔb andφ,Θ: inΔb-Θplane whileλ=0.75

图10 λ=1.5时Δb与φ和Θ的关系Fig.10 Relationship betweenΔb and φ,Θwhileλ=1.5

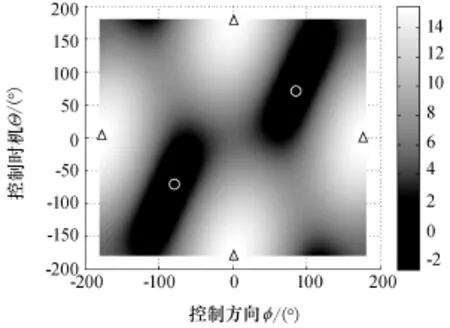
图11 λ=1.5时Δb在φ和Θ平面内的投影Fig.11 Δb projection in control direction-control time plane whileλ=1.5

图12 λ=1.5时Δb与φ和Θ的关系(Δb和φ面内投影)Fig.12 Projection relationship betweenΔb andφ,Θ: inΔb-φplane whileλ=1.5

图13 λ=1.5时Δb与φ和Θ的关系(Δb和Θ面内投影)Fig.13 Projection relationship betweenΔb andφ,Θ: inΔb-Θplane whileλ=1.5

图14 λ=2.5时Δb与φ和Θ的关系Fig.14 Relationship betweenΔb and φ,Θwhileλ=2.5

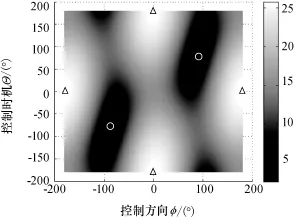
图15 λ=2.5时Δb在φ和Θ平面内的投影Fig.15 Δb projection in control direction-control time plane whileλ=2.5

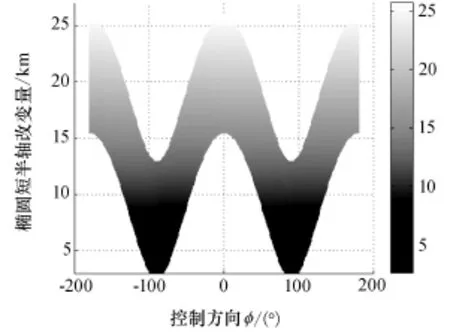
图16 λ=2.5时Δb与φ和Θ的关系(Δb和φ面内投影)Fig.16 Projection relationship betweenΔb andφ,Θ: inΔb-φplane whileλ=2.5

图17 λ=2.5时Δb与φ和Θ的关系(Δb和Θ面内投影)Fig.17 Projection relationship betweenΔb andφ,Θ: inΔb-Θplane whileλ=2.5

图3、图7、图11和图15具有分布相同的四个极大值点(图中用△标出):φ=0°,Θ=±180° (下点横向控制)和φ=±180°,Θ=0°(上点反横向控制),表明无论λ取值如何,在上点反横向或下点横向控制都是最大效率增大椭圆短半轴的方式,与结论1相符。

图3中五个极小值点(图中用○标出):φ=0°,Θ=0°(上点横向控制)和φ=±180°,Θ=±180° (下点反横向控制),表明当λ＜1/2时,在上点横向或下点反横向控制是最大效率减小椭圆短半轴的方式,与结论2相符。

图11和图15具有分布相同的两个极小值点:φ=90°,Θ=90°(左点径向控制)和φ=-90°, Θ=-90°(右点反径向控制),表明当λ＞1时,在左点径向或右点反径向控制,对椭圆短半轴大小改变效率最低,与结论4中“极大浪费燃料”改变椭圆大小的理论推导相符。

图7中四个极小值点的相关数据如表1所示。

表1 λ=0.75时四个极小值点控制方向与矢径方向的关系Tab.1 Relationship between control direction and radius vector in 4 minimum points whileλ=0.75

由表1可知,四个极小值点对应控制方向和矢径方向基本垂直(k1k2→-1),k1k2与-1的微小差别与仿真步长相关,当仿真步长趋近于无限小时,k1k2=-1。即当1/2＜λ＜1时,垂直于矢径方向进行控制最大效率减小椭圆短半轴,与结论3相符。

对不同λ取值区间的仿真结果均验证了理论推导的正确性。实际应用时,考虑节省燃料原则,若需减小椭圆短半轴,最多将椭圆短半轴减小到0即可,选择在相对运动椭圆上点横向控制或在下点反横向控制,控制量ΔV=nΔb/2最小。最终得到关于最大效率改变椭圆短半轴的控制方向和控制时机匹配关系:在相对运动椭圆上下点进行横向或反横向控制,是最大效率改变椭圆短半轴的控制方式(其中:在上点反横向或下点横向控制最大效率增大椭圆短半轴;在上点横向或下点反横向控制最大效率减小椭圆短半轴)。

7 结束语

本文在笔者团队前期对共面伴飞相对运动椭圆短半轴大小控制效率问题研究的基础上,基于Hill方程和二元函数极值理论,系统地对共面伴飞问题中控制方向和控制时机对椭圆短半轴大小控制效率的影响进行了推导,并通过仿真对理论推导进行了验证。研究成果可用于航天器共面伴飞控制中相对运动椭圆短半轴的最省燃料控制问题求解。此外,本文提供了一种共面伴飞控制中最省燃料控制问题的求解思路。下一步,笔者将在此基础上继续对航天器共面伴飞控制中其他参量的最省燃料控制问题进行求解,并对各参量的耦合控制问题进行深入研究。

[1] 李焱,康开华.美国空间监视系统最新发展及趋势分析[J].航天器工程,2008,17(2):76-82.

LI YAN,KANG KAIHUA.Research and analysis on development of US space based surveillance system[J]. Spacecraft Engineering,2008,17(2):76-82.

[2] 任飞.美发射近地轨道监视卫星[J].中国航天,2014(10):23-24.

REN FEI.Space surveillance craft launched by Delta 4 rocket[J].Aerospace China,2014(10):23-24.

[3] 张召才.美国深挖小卫星潜力,欲提升军事用天能力[J].卫星应用,2015(2):37-44.

[4] 张育林,曾国强,王兆魁,等.分布式卫星系统理论及应用[M].北京:科学出版社,2008:25-40.

ZHANG YULIN,ZENG GUOQIANG,WANG ZHAOKUI,et al.Fundamentals of near-earth spacecraft orbit[M].Beijing:Science Press,2008:25-40.

[5] 曾国强,张育林.编队飞行队形设计一般化方法[J].中国空间科学技术,2003,23(1):12-16.

ZENG GUOQIANG,ZHANG YULIN.Generalized method of formation flying configuration design[J]. Chinese Space Science and Technology,2003,23(1):12-16.

[6] 韦娟,袁建平.小卫星编队飞行的相对运动学方程研究[J].飞行力学,2002,20(2):29-32.

WEI JUAN,YUAN JIANPING.Research of relative kinematics on small satellite formation flying[J]. Flight Dynamics,2002,20(2):29-32.

[7] 吴会英,陈宏宇,余勇,等.远距离轨道接近及绕飞控制技术研究[J].中国空间科学技术,2010,30(1): 25-33.

WU HUIYING,CHEN HONGYU,YU YONG,et al.Study of long-distance approaching and companion flying technology[J].Chinese Space Science and Technology,2010,30(1):25-33.

[8] 吴会英,陈宏宇,周美江,等.伴随卫星轨控时机与相对运动椭圆大小控制效率的关系 [J].载人航天, 2013,19(5):90-96.

WU HUIYING,CHEN HONGYU,ZHOU MEIJIANG,et al.Research on relation between orbit control time and control efficiency of company satellites[J].Manned Spaceflight,2013,19(5):90-96.

[9] 郗晓宁,王威,高玉东.近地航天器轨道基础[M].长沙:国防科技大学出版社,2003:244-251.

XI XIAONING,WANG WEI,GAO YUDONG.Fundamentals of near-earth spacecraft orbit[M].Changsha: National University of Defense Technology Press,2003:244-251.

[10] 吴会英,周美江,齐金玲.基于迹向控制量的编队星群相位控制[J].空间控制技术与应用,2014,40(6): 31-35.

WU HUIYING,ZHOU MEIJIANG,QI JINLING.Formation phase control based on the along-track control strategy[J].Aerospace Control and Application,2014,40(6):31-35.

作者简介

周美江 1989年生,2012年获哈尔滨工业大学飞行器设计专业硕士学位,工程师。研究方向为航天器轨道动力学与控制。

Minimum Fuel Control of Relative Ellipse Semi-Minor Axis in Micro/nano-Satellite In-Plane Companion-Flying

ZHOU Meijiang WU Huiying QI Jinling
(Shanghai Engineering Center For Microsatellites,Shanghai 201203)

In-plane companion-flying;Hill equation;Ellipse semi-minor axis;Minimum fuel control;Control time;Control direction;Micro/nano satellite

10.3780/j.issn.1000-758X.2015.05.004

(编辑:高珍)

2015-04-01。收修改稿日期:2015-05-26