基于谐波平衡法的微振动被动控制动力学研究

朱恩涌 魏传锋

(中国空间技术研究院载人航天总体部,北京100094)

基于谐波平衡法的微振动被动控制动力学研究

朱恩涌 魏传锋

(中国空间技术研究院载人航天总体部,北京100094)

为了探究航天器被动隔振系统参数对隔振效果的影响,用变形的三次多项式函数描述粘弹性隔振器的非线性刚度,用分数导数阶算子表征隔振器的阻尼特性,建立了微重力状态下被动隔振系统非线性动力学模型,用谐波平衡法对动力学微分方程进行求解,计算隔振系统的振动传递率,然后探讨了隔振器以及隔振对象的刚度、阻尼、质量对隔振效果的影响。研究结果表明,隔振器非线性阻尼项对系统隔振效果影响很大,被隔振对象的质量对隔振系统共振峰值的影响与非线性阻尼系数的大小密切相关。

隔振;动力学模型;谐波平衡法;振动传递率;非线性;航天器

1 引言

航天器的微重力环境将为生命学、材料学、燃烧学、基础物理学等研究提供良好的研究条件[1]。但是航天员活动或散热风扇、各种液气泵、控制力矩陀螺等设备的工作都会产生微振动激扰源,在一定频率范围内会破坏微重力环境[2]。微振动具有幅值低、振动频率较高的特点[3],工程上通常对振源和有效载荷都进行隔振控制[4]以减小其影响。采用粘弹性材料的被动隔振技术由于可靠性高,可实施性强,能有效控制高频振动,已成为航天器隔振设计的热点。

被动隔振系统动力学研究的关键在于建立准确的动力学模型,一些学者已经开始了相关研究[3]。Liu等[5]不考虑非线性因素研究了隔振器参数对整星隔振系统隔振性能的影响。陈安华等[6]研究了隔振材料的非线性刚度对隔振效果的影响。张业伟等[7]建立了离散型隔振系统的非线性等效动力学模型,研究了隔振系统的振动传递率受激励幅值的影响。但目前的研究在建立动力学模型时并不够准确,没有全面考虑隔振器和隔振对象的质量、刚度和阻尼对系统的影响。

本文以对航天器微振动振源隔振为研究对象,在建模过程中,考虑了隔振器和隔振对象的质量、刚度和阻尼对系统的影响,并尝试用变形的三次多项式函数描述粘弹性隔振器的非线性刚度,用分数导数阶算子表征隔振器的阻尼特性,力求建立更为准确的隔振系统非线性动力学模型,用谐波平衡法推导出振动传递率的解析表达式。然后根据数值解探讨隔振器以及隔振对象的刚度系数、阻尼系数、质量对隔振效果的影响,得出相关设计原则,为航天器被动隔振系统设计提供理论参考。

2 微重力下隔振系统动力学模型

目前,针对复杂结构的动力学分析主要有两种方法:模态参数分析和有限元分析。有限元分析方法简单直观,易于操作[8],但不利于参数修改,也不能得到各参数间的解析表达式。因此本文采用模态参数进行分析,利用集中质量法建立隔振系统动力学模型。将隔振系统简化为由2个子结构组成,一个为隔振对象结构系统,另一个为隔振器结构系统。假设系统只沿一个方向振动,建立的隔振系统动力学模型如图1所示。

受粘弹性材料特性的影响,隔振器的刚度和阻尼将呈非线性。刚度为相对位移的函数,其描述方式有多种。这里采用三次多项式[9]描述弹性力:Fk1=k1x+βk1x3,其中β为隔振器非线性刚度系数。采用Riemman-Liouville分数导数[10]所描述的分数导数阻尼力Fc1=c1Dq(x),

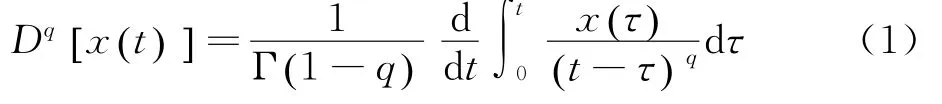
式中 q为分数导数算子的阶数,0＜q＜1。q值越小,表明阻尼的非线性越强。

在与平台固连的坐标系下观察,采用拉格朗日方程,建立系统动力学微分方程:

图1 被动隔振系统动力学模型Fig.1 Passive vibration isolation system dynamic model

对式(2)进行简化后,得到系统动力学微分方程:

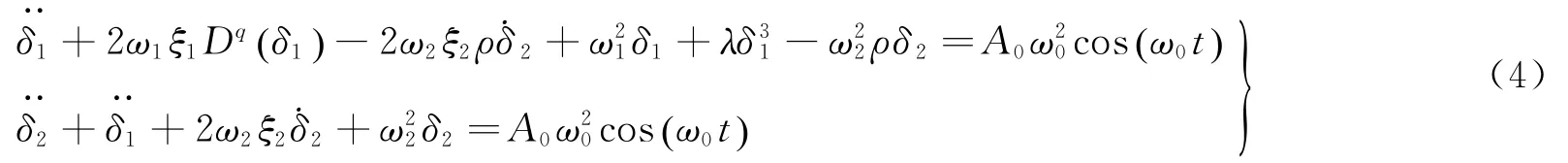
3 振动传递率

系统的隔振性能通常用振动传递率T来描述[11]。T为隔振对象的振动幅值与隔振器底端振动幅值之比。若T＜1,则说明产生隔振效果,并且T的值越小,隔振效果越好。为了得到隔振对象的振动位移,采用谐波平衡法对式(4)进行求解。令

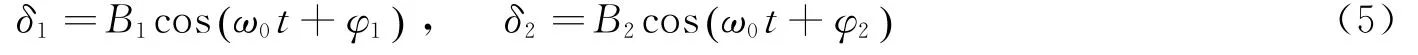
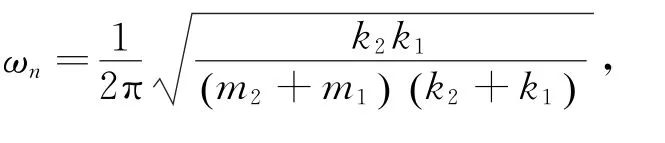
4 参数对振动传递率的影响

在隔振系统的设计中隔振器的刚度、质量和阻尼是重要的设计参数,因此研究三者与隔振效果评价参数振动传递率的之间关系是十分必要的。另外,若掌握隔振对象的参数对振动传递率的影响,也便于在方案设计之初就进行有针对性的设计,从而从设计上主动降低振动响应。为此,通过改变系统激励频率,采用数值法对式(7)和(8)进行求解,并分别改变系统参数,得到一系列数值仿真结果。

首先考察隔振器刚度的变化对系统隔振效果的影响。改变刚度非线性系数β,求解方程组,得到振动传递效率与β的关系,如图2所示。随着频率增加,隔振系统振动传递率从初始值1开始逐渐增大,达到系统共振频率时,产生共振峰,振动传递效率达到最大值,然后再逐渐减小。当T＜1时,隔振系统能产生有效的隔振。随着频率的增大,T越来越小,隔振效果也越强。这也证明了被动隔振系统的隔振效果仅对高频产生隔振效果,而对低频则不能产生隔振[1]。当β分别取不同值时,系统振动传递率并没有发生变化。因此,非线性刚度系数β对振动传递率的影响可以忽略。

求解方程组还可以得到k1对T的影响,如图3所示。从图中可以看出,随着k1的减小,共振峰逐渐前移,这是因为随k1的减小,系统固有频率也减小了。T＜1时,所对应的频率变小,说明能够产生隔振的频率范围变大。另外,随着k1的减小,共振峰值也变小,而且T＜1后,相同频率对应的振动传递率值也变小。因此,减小隔振器刚度有利于提高隔振效果。但是若隔振器刚度降低到一定程度之后,隔振器将呈现明显的柔性特征,隔振系统的运动将不能只用一个自由度表征,所建立的动力学模型将不再适用。

改变隔振对象的刚度k2值,计算振动传递率,得到图4所示关系。从图中可以看出,隔振对象刚度的变化也会造成共振频率的变化,但是由于隔振对象的刚度通常大于隔振器刚度,固有频率对隔振对象刚度敏感度相对降低,因此共振频率变化相对不明显。共振峰值随刚度的增大有所减小,但是变化也不大。

下面再分析隔振器阻尼非线性项与振动传递率的关系。从图5中可以看出,随着阻尼非线性项系数q增大,共振频率没有变化,共振峰的幅值明显减小。因此,降低隔振器阻尼的非线性,有利于减小共振时的振动传递率。

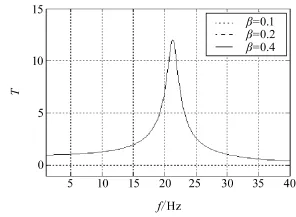
图2 隔振器非线性刚度系数β对振动传递率的影响Fig.2 Effects of vibration isolator nonlinear stiffness coefficientβto vibration transmissibility

图3 隔振器刚度k1对振动传递率的影响(K1为初始刚度)Fig.3 Effects of vibration isolator stiffness k1to vibration transmissibility(K1is initial stiffness)

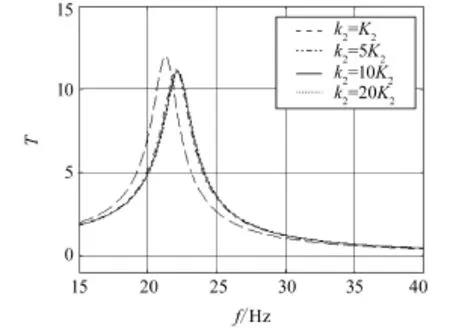
图4 隔振对象刚度k2对振动传递率的影响(K2为初始刚度)Fig.4 Effects of vibration isolation object stiffness k2to vibration transmissibility(K2is initial stiffness)

图5 阻尼非线性项系数q对振动传递率的影响Fig.5 Effects of nonlinear damping coefficient q to vibration transmissibility

改变隔振器阻尼比ξ1的值,得到不同阻尼比对应的振动传递率,如图6所示。从图中可以看出,随着隔振器阻尼比ξ1增大,共振峰的幅值也明显减小。但在高频处,阻尼增大,隔振效果反而变差。因此,与非线性阻尼系数一样,增大隔振器阻尼比能有效抑制共振峰,但在高频处隔振效果变差。

改变隔振对象的阻尼比ξ2的值,得到不同阻尼比对应的振动传递率,如图7所示。从图中可以看出,随着隔振器阻尼比ξ2增大,共振峰的幅值有所减小。因此,增大隔振对象阻尼是有利于抑制共振峰,但效果较弱。

进一步考察隔振器质量变化对振动传递率的影响,如图8所示。随着m1的增大,共振峰明显减小,并且共振频率也减小。这是因为m1的减小,系统固有频率降低。T＜1时所对应的频率变小,T＜1后相同频率对应的振动传递率值也变小。说明能够产生隔振的频率范围变大,并且隔振效果更好。因此增加隔振器质量,能明显提高隔振效果。但是通常隔振器的质量受到航天器质量的限制,因此在设计时需要权衡考虑。

考察隔振对象质量变化对振动传递率的影响,如图9所示。随着m2的变化,固有频率和共振峰都有变化,但是共振峰幅值并不呈现单调的增加或减少。为此,进一步求解非线性阻尼项q取不同值时,不同m2系统振动传递率的共振峰值,如图10所示。

图6 隔振器阻尼比ξ1对振动传递率的影响Fig.6 Effects of vibration isolator ratio of dampingξ1to vibration transmissibility

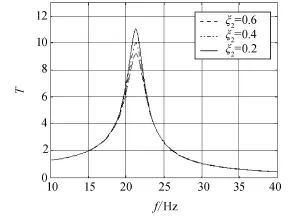
图7 隔振对象阻尼比ξ2对振动传递率的影响Fig.7 Effects of vibration isolation object ratio of dampingξ2to vibration transmissibility

图8 隔振器质量m1对振动传递率的影响(M1为初始质量)Fig.8 Effects of vibration isolator mass m1to vibration transmissibility(M1is initial mass)

从图10中可以看出,当q=1时,隔振器阻尼不存在非线性因素,此时,共振峰的幅值呈单调递增的变化趋势。当q=0.8时,共振峰的幅值呈现先增加而后减小的变化趋势。当q=0.5时,共振峰的幅值呈逐渐减小的变化趋势。因此,说明由于阻尼的非线性,造成振动传递率并不随隔振对象的质量变化而单调变化。不过从图10中看出,即便峰值的变化与q的取值有密切关系,但是由于m2增大后,系统共振频率降低,有效隔振频率范围增大,其对应的振动传递率也减小。

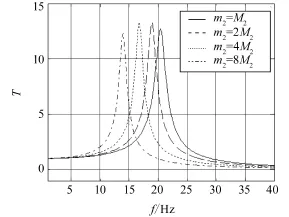
图9 隔振对象质量m2对振动传递率的影响(M2为初始质量)Fig.9 Effects of vibration isolation object mass m2to vibration transmissibility(M2is initial mass)

图10 不同隔振对象质量m2对应的最大振动传递率Fig.10 The most vibration transmissibility among different vibration isolation object mass m2

5 结束语

本文通过建立微重力状态下的隔振系统动力学模型,采用谐波平衡法推导了振动传递率计算公式,综合考虑了隔振器和隔振对象的质量、刚度和阻尼对系统的影响,得出了系统参数对振动传递率的影响,为航天器被动隔振系统设计提供参考。主要有以下结论:

1)隔振器的非线性刚度项对系统隔振效果影响不明显,非线性阻尼项对系统隔振效果影响很大,增大阻尼非线性系数,能有效抑制系统共振峰值,但在高频处隔振效果变差。

2)隔振器的质量和刚度对系统隔振效果影响明显。增大质量或减小刚度,均能有效提高隔振效果,扩大隔振频率范围。

3)增大被隔振对象的阻尼和刚度能降低共振频率处的振动传递率。

4)被隔振对象质量对隔振系统共振峰值的影响与非线性阻尼系数的大小密切相关。但是由于质量增加能减小共振峰频率,因此也有利于提高隔振效果。

[1] GRODSINSKY,CARLOS M,WHORTON MARK S.A survey of active vibration isolation systems for microgravity applications[R].Huntsville:Marshall Space Flight Center,2000.

[2] 邓峰岩,和兴锁,张娟,等.微振动对空间实验室微重力环境的影响研究[J].振动与冲击,2005,24(3):103-107.

DENG FENGYAN,HE XINGSUO,ZHANG JUAN,et al.Research on the effects of microgravity vibration environment in the spacelab[J].Journal of Vibration and Shock,2005,24(3):103-107.

[3] 张振华,杨雷,庞世伟.高精度航天器微振动力学环境分析[J].航天器环境工程,2009,26(6):528-534.

ZHANG ZHENHUA,YANG LEI,PANG SHIWEI.Jitter environment analysis for micro-precision spacecraft[J].Spacecraft Environment Engineering,2009,26(6):528-534.

[4] WHORTON,MARK S.Microgravity vibration isolation for the international space station[R].Huntsville: Marshall Space Flight Center,2000.

[5] L K LIU,G T ZHENG.Parameter analysis of PAF for whole-spacecraft vibration isolation[J].Aerospace Science and Technology,2007,11(6):464-472.

[6] 陈安华,刘德顺,朱萍玉.被动隔振体的非线性振动分析[J].机械工程学报,2001,37(6):99-101,105.

CHEN ANHUA,LIU DESHUN,ZHU PINGYU.Nonlinear response analysis of a passively vibration-isolated body[J].Chinese Journal of Mechanical Engineering,2001,37(6):99-101,105.

[7] 张业伟,方勃,李松,等.整星隔振平台的阻尼非线性对隔振性能影响的物理机理 [J].振动与冲击, 2011,30(10):173-176.

ZHANG YEWEI,FANG BO,LI SONG,et al.Physical mechanism for effect of nonlinear damping of a whole-spacecraft vibration isolation platform on its vibration-isolation behaviors[J].Journal of Vibration and Shock,2011,30(10):173-176.

[8] ANIL K CHOPRA.Dynamics of structures:theory and applications to earthquake engineering[M].3rd ed.New Gersey:Pearson Education Inc.,2007:447-466.

[9] PELEG K.Frequency response of non-linear single degree of systems[J].International Journal of Mechanical Science,1979,21:75-84.

[10] JOSEPH P,YUEHUA G.General response of viscoe lastic systems modeled by fractional operators [J].Franklin Institute,1988,325(2):247-275.

[11] 方勃,李松,黄文虎.新型整星隔振系统动力学分析[J].振动工程学报,2012,25(2):193-198. FANG BO,LI SONG,HUANG WENHU.Analysis of dynamics for the new whole-spacecraft vibration isolator[J].Journal of Vibration Engineering,2012,25(2):193-198.

[12] 闫启方,刘林超,陈哲.分数算子描述的两级粘弹性阻尼隔振系统的幅频特性分析 [J].噪声与振动控制, 2006,26(2):7-10.

YAN QIFANG,LIU LINCHAO,CHEN ZHE.Analysis of magnitude-frequency of two-stage mounting isolation system by fractional derivate operator[J].Noise and Vibration Control,2006,26(2):7-10.

Research on Passive Control Dynamics of Micro-vibration Based on Harmonic Balance Method

ZHU Enyong WEI Chuanfeng
(Institute of Manned Space System Engineering,China Academy of Space Technology,Beijing 100094)

For investigating the effects of passive vibration isolator parameters on the vibration transmissibility,nonlinear stiffness characteristics of the vibration isolating material was described by the cubic polynomial function of its deformation,and the nonlinear damping was characterized by viscoelastic fractional derivative operator.The nonlinear dynamic model in microgravity environment of passive vibration isolator system was developed.The dynamic response characteristics were analyzed by the harmonic balance method,and the vibration transmissibility was obtained.Then the influence of stiffness,damping and mass of the isolator and isolated body on vibration isolation effect were analyzed.The results provide theoretic reference for design of spacecraft isolators.The results show that the effects of vibration isolator nonlinear damping coefficient on vibration transmissibility were obvious and the effects of vibration isolation object mass on resonance vibration peak value have a great deal to do with the vibration isolator nonlinear damping coefficient.

Isolation;Dynamic model;Harmonic balance method;Vibration transmissibility; Nonlinear;Spacecraft

10.3780/j.issn.1000-758X.2015.05.007

(编辑:高珍)

2015-03-07。收修改稿日期:2015-05-21

朱恩涌 1983年生,2010年获武汉大学机械设计及理论专业博士学位,高级工程师。研究方向为载人航天器动力学与总体设计。