上覆土层节理岩质边坡稳定性数值分析

张 建，赵建平

(中南大学 资源与安全工程学院，长沙 410083)

上覆土层节理岩质边坡稳定性数值分析

张 建，赵建平

(中南大学 资源与安全工程学院，长沙 410083)

采用Mohr-Coulomb和Ubiquitous-Joint本构模型，运用强度折减法，研究节理面倾向与倾角、土层与岩层的厚度比例对上覆土层节理岩质边坡稳定性的影响。结果表明： 节理面顺倾角度大小与岩体中岩石的内摩擦角接近时，坡体稳定性较差，破坏区域较大；节理面反倾角度与坡体潜在破坏裂隙近似正交时，坡体稳定性较好； 随着坡角的增大，节理面倾角变化对坡体稳定性的影响逐渐减弱；当节理面倾角大于坡角时，边坡角度是影响坡体稳定性的主要因素； 上覆土层厚度小于4m时，安全系数随土层厚度的增加而增大，土层厚度大于4m时，安全系数随土层厚度的增加而减小；上层土体的厚度较小时，应重点对坡脚处进行支护；上层土体厚度接近或超过坡高一半时，应重点对上层土体临空侧进行支护。

节理岩质边坡；上覆土层；Ubiquitous-Joint模型；强度折减法；稳定性；破坏形式；数值分析

1 研究背景

节理岩质边坡分布广泛，构造复杂，稳定性分析难度较大，对节理岩质边坡稳定性的研究仍然是边坡稳定性分析的重要内容[1-2]。白云峰等[3]、陈从新等[4]、龚文惠等[5]、蔡跃等[6]基于不同方法和视角对节理岩质边坡岩层倾向与坡体破坏形式的关系等问题进行了相关研究。鲁光银等[7]通过数值模拟的方式，对层状岩体的破坏模式和各向异性特征进行了分析。林杭等[8]采用实体单元模拟结构面，将岩体中的结构面作为连续介质处理，分析了优势结构面不同倾角时坡体的破坏形式。柳群义[9]、卢敦华等[10]采用遍布节理模型，分别研究了结构面倾角对坡体破坏形式的影响和结构面参数对边坡稳定性及破坏模式的影响。黄书岭等[11]针对已有本构模型的局限性，开发了层状岩体复合材料硬化-软化模型，实现了非线性数值计算功能。赵炼恒[12]等还研究了动态条件下节理岩质边坡的稳定性问题。

以往对节理岩质边坡的研究，多数研究者将其模型简化为含一组平行贯通结构面的岩质坡体。然而在现实中，即使对于包含了优势节理面的岩质边坡而言，岩体中节理的分布也是不规律的，通常是贯通性参差不齐，走向各异，岩体表现出明显的各向异性特征，而对结构面的简化处理弱化了岩体的各向异性特征，与实际情况有较大偏差。此外，不论是自然边坡还是人工开挖边坡，由于自然风化作用和地质构造作用等原因，岩质边坡在近地表层常常覆盖了一层土体或近似土体的软岩体，土层与岩层的厚度比例不同时，坡体潜在破坏位置也会有差别，以往的研究鲜有涉及类似问题。基于以上分析，本文在已有的研究成果之上，采用数值分析方法，分析散碎非连续节理分布特征对坡体稳定性的影响，以及土层与岩层的厚度比例不同时坡体潜在破坏位置的分布规律，为类似地质状况的边坡治理提供参考。

2 本构模型原理

数值分析采用有限差分软件FLAC3D，上覆土层的计算本构模型选用Mohr-Coulomb模型，节理岩体的本构模型选用Ubiquitous-Joint模型(遍布节理模型)[13]。Ubiquitous-Joint模型是包含了Mohr-Coulomb体内特殊方向上结构面各向异性特征的弹塑性本构模型，它的特点是在数值计算过程中，先计算每个计算时步更新的应力，再应用相应的塑性修正法则判别岩体单元的总体破坏情况，在数值分析过程中同时考虑结构面的剪切与拉伸破坏。

图1 Ubiquitous-Joint模型中结构面破坏准则Fig.1 Failure criterion of structural plane in Ubiquitous-Joint model

在图1中，AB段的破坏包络线表征剪切破坏，BC段表征拉伸破坏，对应的方程分别为：

fs=τ+σ3′3′tanφj-cj=0 ;

(1)

(2)

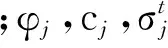
(3)

在计算过程中，程序会根据岩体的应力状态进行塑性修正，当岩体处于弹性状态时，不需要对其进行塑性修正，当岩体处于塑性状态时，会根据相关流动法则对其进行塑性修正。

Ubiquitous-Joint模型对节理面的处理与以往研究中将节理面简化为连续介质的平行贯通结构面的处理方式不同，节理面呈现出散碎非连续特征，均匀分散在岩体内部，与实际情况更接近。

3 数值模型与计算参数

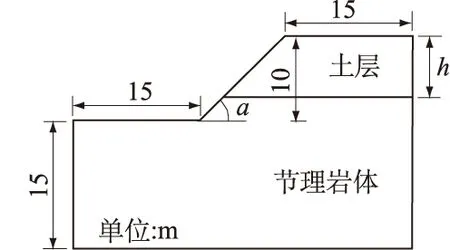
图2 数值分析模型Fig.2 The slope model of numerical analysis

通过试算方法确定分析模型的最佳边界尺寸：边坡高度10m，左边界、右边界、下边界范围均取值15m，模型总高度为25m，坡角α取值[30°, 90°]，土层厚度h的取值范围为[0, 10]。取模型厚度为2m。模型的平面形状及尺寸见图2。

分析中模型下边界采用全约束，左右边界法向约束，上部为自由边界，以解算平衡状态的安全系数和坡体的塑性区分布及剪应变增量云图作为主要分析对象。上层土体的计算本构模型选用Mohr-Coulomb模型，节理岩体的计算本构模型采用Ubiquitous-Joint模型。节理岩体中包含了岩石与结构面，赋值参数各不相同，为使分析结论具有普适性，综合文献[9-11]中选用的一般边坡岩土质参数，确定本文分析的岩、土、节理面参数，具体计算参数见表1。

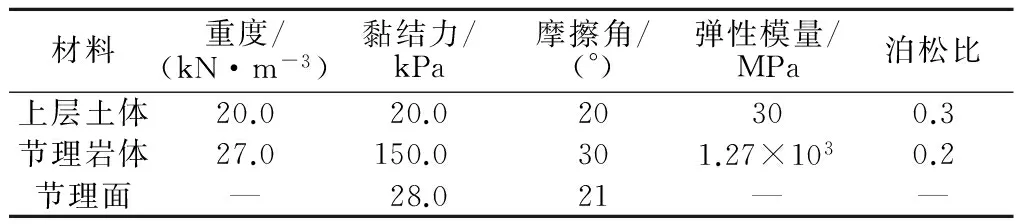
表1 计算参数Table 1 Calculation parameters

4 分析与讨论

4.1 节理面倾向与倾角对坡体稳定性的影响

按照图2的模型，节理面的走向与模型厚度方向平行，顺倾情况下，节理面的倾倒方向向右，反倾情况下，节理面的倾倒方向向左，顺倾节理面倾角定义为β，反倾节理面倾角定义为λ。

为探究坡角与土层厚度一定的情况下节理面倾角变化时坡体的稳定性变化规律及破坏特征，取上覆土层厚度h=5 m，坡角取值α时，顺倾节理面倾角β与反倾节理面倾角λ分别由0°递增至90°，递增幅度为10°，记录各情形下的边坡安全系数取值及临界状态下坡体的剪应变增量云图。其中坡角α有8组取值，分别为30°,40°,45°,50°,60°,70°,80°,90°。

4.1.1 节理面顺倾情形

随着节理面倾角的逐渐增大，计算所得安全系数有如下分布特征： 不同坡角取值时，随着节理倾角的增大，安全系数均呈现减小-增大-减小的变化趋势，所有的节理面倾角与安全系数的函数曲线均存在一个最小值和一个最大值。最小值随着边坡角度的增大逐渐向右偏移。 随着坡角取值的增大，节理面倾角与安全系数的函数曲线越来越平缓。

探讨坡角α一定时节理面与坡面夹角大小对坡体安全系数的影响。由于坡角α一定时，节理面倾角可能大于α，也可能小于α，而且2种情况下夹角大小对坡体稳定性的影响不相同，故作以下定义：将节理面倾角大于坡角时，两者的夹角称之为陡倾夹角；而节理面倾角小于坡角时，两者的夹角称之为缓倾夹角。由于坡角与节理面倾角均在[0°,90°]取值，故不同坡角对应的陡倾夹角个数与缓倾夹角个数不相同。本次分析中，讨论坡角在[30°,70°]之间取值的情况，陡倾夹角与缓倾夹角对边坡稳定性的影响分别见图3(α为坡角，β为顺倾节理面倾角)。

分析图3(a)可知，坡角较小时，安全系数随陡倾夹角的增大呈先增大后减小的变化趋势;坡角取较大值时，安全系数呈递减变化。这是由于坡角较小且节理面陡倾夹角取值较小时，节理面倾角大小与岩体中岩石的内摩擦角取值相近，此时坡体的安全系数最小。当坡角取值较大时，坡体自重作用对下滑力的作用增强，因自重方向竖直向下，陡倾夹角越大，节理面倾角越与重力方向一致，越容易沿节理面产生滑移破坏，安全系数越小。分析图3(b)可得，随着缓倾夹角的增大，安全系数呈先减小后增大的变化趋势，函数曲线存在一个最小值，这是由于当顺倾节理面倾角与岩石内摩擦角接近时，坡体最容易产生沿节理面的滑移破坏，表现为安全系数取最小值，之后随缓倾夹角的增大(即节理面倾角的减小)，坡体越来越稳定，表现为安全系数逐步递增。

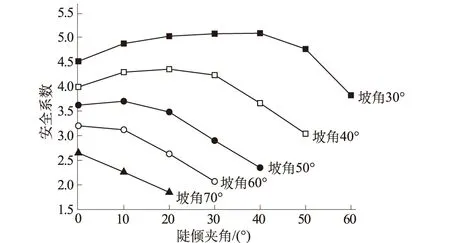
(a) β>α

(b) β<α

图4 反倾情形下节理面与坡面夹角对坡体稳定性的影响Fig.4 Influence of the intersection angle between anti-dip joint and slope surface on the slope stability

4.1.2 节理面反倾情形

分析节理面反倾情形下节理面与坡面夹角对坡体稳定性的影响。讨论坡角在[30°,70°]之间取值的情况，节理面倾角λ的取值范围为[0°,90°]，定义节理面反倾情形下节理面与坡面夹角为γ。计算结果如图4。分析图4可知：坡角α取值一定时，随着节理面与坡面的夹角γ逐渐增大，安全系数均呈现先增大后减小的变化趋势，节理面与坡面夹角取值[80°,120°]时，安全系数相对取值较大，根据莫尔-库伦破坏理论[14]，假定坡体内潜在破坏面优先沿着顺坡向以岩石内摩擦角大小的一半+45°的角度(60°)产生，而此时的节理面与该破坏面的夹角在90°左右，节理面与潜在破坏面近似正交，坡体相对较安全。

4.1.3 节理面分布形式对坡体破坏特征的影响

对坡角α取值为30°,40°,45°,50°,60°,70°,80°,90°，节理面分别顺倾[0°,90°]与反倾[0°,90°]的情况进行分析，以计算平衡状态下坡体的塑性区分布和剪应变增量云图作为主要分析对象。将坡体中存在剪应变增量的区域定义为坡体的潜在破坏区，以计算平衡状态下坡体的剪应变增量云图作为分析对象，分析发现：坡角一定时，节理面顺倾角度在[10°,30°]范围内时，坡体的破坏范围较大，上层土体与下层岩体均存在大面积剪应变增量区域；节理面反倾角度在[60°,80°]时，与顺倾时类似，上层土体与下层岩体均存在大面积剪应变增量区域。在分析过程中发现坡脚(图5中的a(4)，a(5)，b(7)，b(8))和坡面与岩土接触界面的交点(图5中a(2)，a(10)，b(9)，b(10))是下层岩体中较容易被破坏的区域，因为坡脚与基岩存在交角，容易产生应力集中，而坡面与岩土接触界面的交点直接承载上覆土层的作用力，故2处易产生破坏。

注：该图为剪应变增量云图，仅用来表征坡体潜在破坏区域的位置，不表示具体数值大小，故省略图例。

4.2 上覆土层厚度对坡体稳定性的影响

以坡角50°的情形为例，研究上覆土层厚度变化时，坡体的稳定性特征及破坏形式。相同土层厚度情形下，分别分析节理面顺倾和反倾2种情况，顺倾与反倾角度均取45°。随土层厚度增加，计算所得安全系数分布规律如图6示，节理面顺倾与反倾情况下，随着土层厚度的增大，安全系数均呈现先增大后减小的变化趋势。土层厚度<6 m时，节理面反倾情况下的安全系数均大于节理面顺倾情况下的安全系数;土层厚度>6 m时，顺倾与反倾情况的安全系数取值相同。 节理面反倾时，安全系数在土层厚度为4 m时发生转折，节理面顺倾时，安全系数在土层厚度为5 m时发生转折，说明上覆土层达到一定高度后，坡体的稳定性急剧下降。

注：该图为剪应变增量云图，仅用来示意潜在破坏区域的位置，不表示具体数值大小，故省略图例。

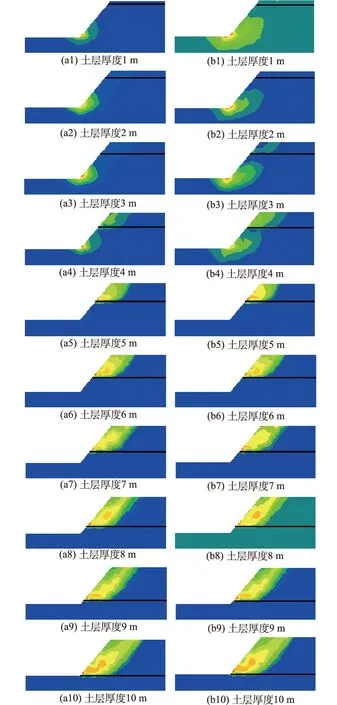
再对土层厚度发生变化时坡体的破坏形式进行分析(如图7)，发现上覆土层厚度<4 m时，坡体的破坏部位主要分布在下层节理岩体中;土层厚度>4 m后，坡体的破坏部位主要分布在上层土体中。结合对图6的分析，上覆土层厚度<4 m时，坡体破坏主要集中在下层节理岩体中，节理面顺倾时，坡体易于破坏，坡体的安全系数较反倾时小。当上覆土层厚度>4 m时，坡体破坏集中在上层土体中，下层岩体较上层土体的破坏难度大，此时的坡体相当于一个匀质土坡，坡体的稳定性取决于上层土体的稳定性，因此节理面的顺倾与反倾状况对坡体的稳定性没有影响，表现为2种情形下的土层厚度与安全系数函数曲线重合在一起。

在图7中，无论节理面顺倾或是反倾，上覆土层厚度<4 m时，坡体的破坏均主要发生在坡脚处，此时坡体的破坏形式主要为剪切破坏。当上覆土层厚度>4 m时，土层成为了坡体的重要组成部分，而其“跟随”岩体破坏而破坏的“依附”特性也随之不存在，此时的土体较下层岩体更容易破坏，在下层岩体发生破坏之前，上层土体已发生显著破坏。经分析此时坡体的破坏形式为拉伸-剪切复合破坏。

通过以上分析，提出以下边坡治理方案：对于覆土节理岩质坡体而言，当土层厚度较小时，边坡重点支护位置为坡脚处;当土层厚度较大(超过边坡高度的一半)时，土层较岩层更容易发生滑坡破坏，应同时对上层土体临空侧和坡脚处进行支护，但重点为上层土体临空侧位置。

5 结 语

(1) 对于上半部分为土质、下半部分为节理岩质的坡体而言，在坡角取值一定、节理面顺倾角度大小与岩体中岩石的内摩擦角接近时，坡体的安全系数最小；反倾节理面倾角变化对坡体稳定性的影响较节理面顺倾时要小。节理面倾向与坡体潜在破坏裂隙近似正交时，坡体稳定性较好。

(2) 节理面在顺倾和反倾情况下，均有坡角越小，坡体稳定性对节理面倾角的变化越敏感;坡角越大，节理面倾角的变化对坡体稳定性的影响越不明显。坡体稳定性受到坡角、节理面、坡体自重等因素的综合作用。当坡角较小时，节理面对坡体稳定性的影响较明显；当坡角较大时，因坡体自重在下滑力中分配比例的增加，节理面对坡体稳定性的影响相对被弱化。

(3) 坡角一定、节理面倾角一定时，无论节理面顺倾还是反倾，上覆土层厚度<4 m时，随土层厚度增加，安全系数越来越大，此时坡体破坏区域主要发生在下层岩体中，坡脚处剪切破坏最严重，应重点支护。土层厚度>4 m时，随土层厚度增加，安全系数越来越小，坡体破坏主要集中在上层土体中，此时坡体的破坏形式为拉伸-剪切复合破坏，需重点对土层临空侧进行加固。

在分析过程中发现结构局部破坏对安全系数的影响较大，仅通过安全系数大小分析边坡稳定性并不十分可靠，尤其对于地质构造复杂、各向异性明显的边坡结构体而言，更应该结合安全系数及其它指标(如关键点的位移量变化特征和剪应变增量云图等)对坡体的稳定性作综合分析。

[1] 赵尚毅, 郑颖人, 邓卫东. 用有限元强度折减法进行节理岩质边坡稳定性分析[J].岩石力学与工程学报,2003,22(2)：254-260. (ZHAO Shang-yi, ZHENG Ying-ren, DENG Wei-dong. Stability Analysis of Jointed Rock Slope by Strength Reduction FEM[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(2):254-260.(in Chinese))

[2] 郑颖人, 陈祖煜, 王恭先, 等. 边坡与滑坡工程治理[M].北京:人民交通出版社,2010:146-193. (ZHENG Ying-ren, CHEN Zu-yu, WANG Gong-xian,etal. Engineering Treatment of Slope & Landslide[M]. Beijing: China Communication Press, 2010:146-193. (in Chinese))

[3] 白云峰, 周德培, 冯 君. 顺向坡岩层走向与边坡走向夹角的上限值[J]. 西南交通大学学报,2005,40(3):326-329. (BAI Yun-feng, ZHOU De-pei, FENG Jun. Upper Limit of Angle between Strikes of Slope and Strata for Dip Slope[J]. Journal of Southwest Jiaotong University, 2005, 40(3): 326-329. (in Chinese))

[4] 陈从新, 黄平路, 卢增木. 岩层倾角影响顺层岩石边坡稳定性的模型试验研究[J].岩土力学, 2007, 28(3):476-481. (CHEN Cong-xin, HUANG Ping-lu, LU Zeng-mu. Study on Correlation between Stability of Consequent Rock Slope and Obliquity of Rock Layer by Simulation Experiment[J]. Rock and Soil Mechanics, 2007, 28(3): 476-481. (in Chinese))

[5] 龚文惠, 王 平, 陈 峰. 顺层岩质路堑边坡稳定性的敏感性因素分析[J]. 岩土力学,2007,28(4):812-816.(GONG Wen-hui, WANG Ping, CHEN Feng. Analysis of Sensitivity Factors to Stability of Bedding Rock Cutting Slope[J]. Rock and Soil Mechanics,2007,28(4):812-816.(in Chinese))

[6] 蔡 跃, 三谷泰浩, 江琦哲郎. 反倾层状岩体边坡稳定性的数值分析[J]. 岩石力学与工程学报,2008,27(12):2517-2522. (CAI Yue, MITANI Y, ESAKI T. Numerical Analysis of Stability for an Antidip Stratified Rock Slope[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(12): 2517-2522.(in Chinese))

[7] LU G Y, ZHU Z Q, LIU Q Y,etal. Failure Mode and Strength Anisotropic Characteristic of Stratified Rock Mass under Uniaxial Compressive Situation[J]. Journal of Central South University, 2009, 16(4): 663-668.

[8] 林 杭, 曹 平, 李江腾, 等.层状岩质边坡破坏模式及稳定性的数值分析[J]. 岩土力学, 2010, 31(10): 3300-3304. (LIN Hang, CAO Ping, LI Jiang-teng,etal. Numerical Analysis of Failure Modes and Stability of Stratified Rock Slopes[J]. Rock and Soil Mechanics, 2010, 31(10): 3300-3304.(in Chinese))

[9] 柳群义.红层路堑边坡稳定性与防治研究[D].长沙: 中南大学, 2010: 54-65.(LIU Qun-yi. Study on the Stability of Road Slope with Red Bedded Rock Mass and Its Reinforcement Technique[D]. Changsha: Central South University, 2010: 54-65.(in Chinese))

[10]卢敦华, 曲艳伟, 何忠明, 等. 结构面强度参数对层状边坡稳定性影响的三维分析[J].中南大学学报(自然科学版), 2011, 42(1)：147-151. (LU Dun-hua, QU Yan-wei, HE Zhong-ming,etal. Three-dimensional Analysis for Effect of Structural Plane Strength Parameters on Stratified Slope Stability[J]. Journal of Central South University (Science and Technology), 2011, 42(1): 147-151. (in Chinese))

[11]黄书岭, 徐劲松, 丁秀丽, 等.考虑结构面特性的层状岩体复合材料模型与应用研究[J]. 岩石力学与工程学报,2010,29(4):743-756. (HUANG Shu-ling, XU Jin-song, DING Xiu-li,etal. Study of Layered Rock Mass Composite Model Based on Characteristics of Structural Plane and Its Application[J]. Chinese Journal of Rock Mechanics and Engineering, 2010,29(4):743-756.(in Chinese))

[12]赵炼恒, 罗 强, 李 亮, 等. 层状岩体边坡动态稳定性拟静力上限分析[J]. 岩土力学,2010,31(11):3627-3634.(ZHAO Lian-heng, LUO Qiang, LI Liang,etal. Upper Bound Quasi-static Analysis of Dynamic Stability of Layered Rock Slopes[J]. Rock and Soil Mechanics, 2010, 31(11): 3627-3634.(in Chinese))

[13]Itasca Consulting Group, Inc. Fast Language Analysis of Continua in 3 Dimensions, Version 3.0, User’s Manual[K]. Minneapolis, MN USA: Itasca Consulting Group, Inc, 2005.

[14]陈仲颐, 周景星, 王洪瑾. 土力学[M]. 北京: 清华大学出版社, 2011: 160-168. (CHEN Zhong-yi, ZHOU Jing-xing, WANG Hong-jin. Soil Mechanics[M]. Beijing: Tsinghua University Press, 2011:160-168. (in Chinese))

(编辑：赵卫兵)

Numerical Analysis of the Stability of JointedRock Slope with Overlying Soil

ZHANG Jian, ZHAO Jian-ping

(School of Resources and Safety Engineering, Central South University, Changsha 410083, China)

The influence of the dip and inclination of joint and the ratio of soil thickness to rock thickness on the stability of jointed rock slope with overlying soil is researched in the present paper. The Mohr-Coulomb and Ubiquitous-Joint constitutive models and strength reduction method are used. Results of numerical simulation reveal that: for consequent-joint slope, when the consequent angle of joint is approximately equal to the internal friction angle of the rock, the safety factor is small and the damage area is large; while for anti-dip rock slope, the safety factor is large when the joint intersects vertically with the potential damage fracture of the slope. The effect of the dip of joint on slope stability reduces with the slope angle increasing. When the dip of joint is larger than the slope angle, slope angle is the main factor affecting the slope stability. When the thickness of soil layer is less than 4 meters, the slope safety factor increases with the thickness of soil layer increasing, and vise versa. When the thickness of the overlying soil is small, the slope toe should be the focus of support work, while the air side of the overlying soil should be supported as the key position when the thickness of the overlying soil is close to or larger than half of the slope height.

jointed rock slope; overlying soil; Ubiquitous-Joint mode; strength reduction method; stability; failure mode; numerical analysis

2014-05-12;

2014-06-17

中南大学中央高校基本科研业务费专项资金资助(2014zzts261)

张 建(1988-),男,河南信阳人, 硕士研究生，从事岩土工程理论与数值分析研究,(电话)15200803993 (电子信箱)zjian29@yeah.net。

10.3969/j.issn.1001-5485.2015.02.022

TU457

A

1001-5485(2015)02-0108-06

2015,32(02):108-113