基于ABAQUS的红黏土地基排水固结沉降分析
赵 蕾,陈 筠,邬忠虎,刘磊磊
(1.贵州大学 资源与环境工程学院,贵阳 550025; 2.中南大学 地球科学与信息物理学院,长沙 410083)
基于ABAQUS的红黏土地基排水固结沉降分析
赵 蕾1,陈 筠1,邬忠虎1,刘磊磊2
(1.贵州大学 资源与环境工程学院,贵阳 550025; 2.中南大学 地球科学与信息物理学院,长沙 410083)
针对红黏土地区地基排水固结过程的复杂性,对红黏土地基排水固结沉降进行数值分析。采用大型通用有限元分析软件ABAQUS/Standard中的固结计算模块Soils和自带的修正剑桥模型,以某铝厂的改造工程项目为算例,对红黏土地基中的沉降随时间的变化规律、孔隙水压力消散规律、孔隙比随深度的非线性分布以及土体的有效应力增长进行了研究。研究表明:计算结果与土力学规律吻合,能准确反映红黏土地基固结沉降的实际情况,可为红黏土地基上的建(构)物改造工程地基处理和工程设计提供参考。
红黏土地基;ABAQUS;修正剑桥模型;固结沉降;孔隙水压力
1 研究背景
20世纪修建的建(构)筑物部分以红黏土为地基,随着城镇化战略的实施,要不断通过对既有建(构)筑物的改造来提高其使用年限,实现可持续发展。为了使既有建(构)筑物改造工程在保证安全的同时,充分利用土体的固结沉降效应[1-2],使设计更加经济合理,首要工作则是需要对红黏土地基固结沉降随时间发展的规律、孔隙水压力消散规律、孔隙比沿着深度分布的规律要有准确的认识。因此,红黏土地基固结沉降计算和沉降规律的研究对指导既有建筑物改造工程中的地基处理和工程设计有着重要的指导意义。
目前,红黏土地基沉降计算方法主要有3类:①理论计算法,如分层总和法[3]、弹性理论公式法等,虽然地基沉降计算理论有了很大的改进,但是由于土性材料的复杂性和各向异性,计算过程中必须采用一些假设作为前提条件,通过理论公式所计算出来的沉降和实测值仍然存在一定差距。②对地基进行沉降观测,根据观测结果可以较准确地预测地基最终沉降量及工后沉降量以指导现场施工,这类方法有:Taylor法、双曲线法[4]、指数曲线法[5]、Asaoka法等[6]。由于这类方法需要现场监测数据,不但操作起来比较困难,而且对施工有一定妨碍,加之施工过程中的很多不确定性因素可能导致监测数据的不准确。③数值计算法,主要有差分法[7]、有限单元法[8]、离散元法。其中,有限元法是目前运用最广泛的数值计算方法,其特点是适应性强,可以较全面地考虑土体的变形及其边界条件,能够方便地处理非均质、非线性、复杂边界条件。基于此,本文利用大型通用有限元软件ABAQUS[9]强大的非线性分析能力,结合工程实例,对红黏土地基固结沉降进行数值分析[10-11]。
2 工程概况
贵州某工厂车间为一层排架结构,高13.5 m,属二类安全等级建筑物,对差异沉降中度敏感。基础埋置深度-1.5 m,基础形式为条形基础。地貌为溶蚀残积地貌。场地土质的分布情况如下。
植物层①:主要由褐黄、灰褐色耕植土组成,含植物根系,结构松散,层厚0.5~1.5 m。红黏土②:褐黄色,硬塑状态,稍湿,层厚0.6~4.30 m,属中等偏低压缩性土。红黏土③:褐黄色,可塑状态,湿,层厚0.9~2.2 m,属中等偏高压缩性土。红黏土④:褐黄色,软塑状态,湿,层厚1.0~3.5 m,属高压缩性土。在地基正式加载前,土体在自重和表面均布荷载10 kPa作用下完成固结,随后地基承受来自于建筑物施加的均布荷载140 kPa,总载荷150 kPa。
为了便于数值分析,依据工程地质勘察报告,将地基影响深度内的主要地层物理力学参数列于表1。

表1 地基土物理力学参数Table 1 Physical and mechanical parameters of foundation soil
3 模型建立
地基变形可简化为平面变形、空间渗流问题,因此,模型选取平面应变进行分析,本构模型选择修正剑桥模型。
3.1 修正剑桥模型
(1)
其中,
(2)

(3)

图1 p-t平面上的修正剑桥模型屈服面Fig.1 Yield surface on p-t plane of modified Cambridge model
式中:pa为初始应力,实际计算中近似取为大气压力;ea为初始孔隙比;λ,κ为剑桥模型的2个参数。λ,κ值可以利用不同的σ3等向压缩与膨胀试验给出。
ABAQUS中的ClayPlasticity模型正是基于塑性理论,在原有的剑桥模型基础上进行了扩展。修正的剑桥模型屈服面如图1所示,屈服面函数与土力学中的表达形式虽略有差异,但实质上都是一样的,屈服面函数[10]为
(4)
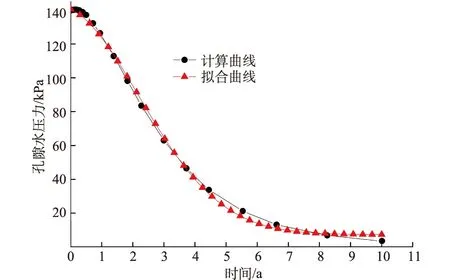
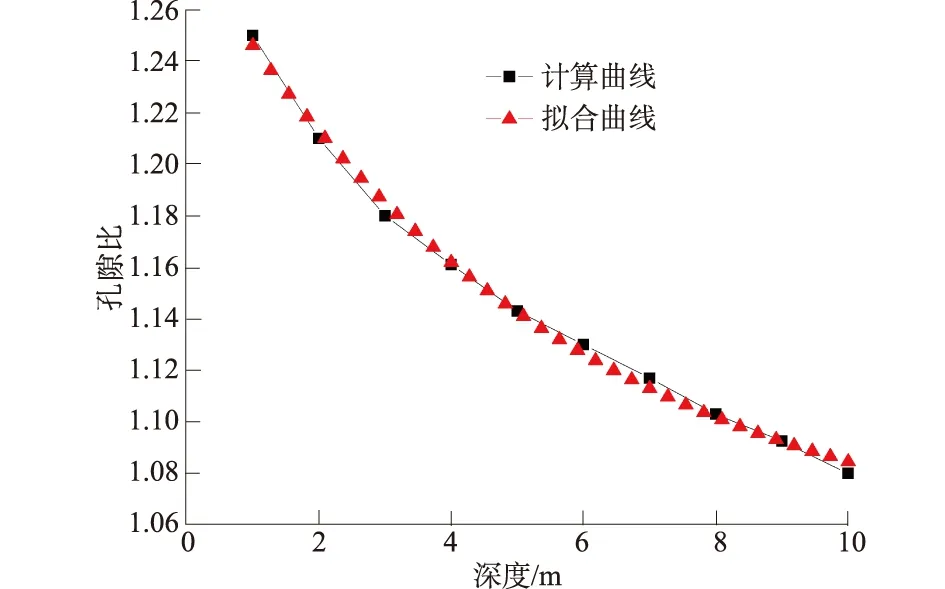
式中:t为偏应力参数;a为椭圆与CSL的交点所对应的p值;β为控制屈服面形状的参数,在t>Mp的一侧β=1,在t 3.2 模型描述 图2 初始平衡状态位移Fig.2 Displacement in initial equilibrium state 该地基的深度影响范围取10m,土层底部不排水,顶面排水,固结时间总长为10a。在基础底部埋设单点沉降计和孔隙水压力计分别对沉降量和孔隙水压力变化值进行监测,由于时间跨度太大,有的监测资料存在缺失,本文仅收集到某几年的实测值,但这并不会对结果产生影响。 土层表面作用的均布荷载150kPa,土体单元采用固体与液体耦合的平面应变单元CPE8RP[16],模型初始平衡状态如图2所示。 3.3 初始条件和边界条件 3.3.1 初始条件 在ABAQUS的Step模块中首先建立名为Ini的Geostatic分析步,通过Geostatic分析步施加一个重力或体积力,使得土体的初始位移为0或近似为0。在Geostatic分析步中,ABAQUS自动获得与给定边界条件相平衡的应力状态,并将这个应力状态作为后续分析的初始应力场。 3.3.2 边界条件 模型中地基的左右两侧水平位移为0,不限竖向位移;地基底部水平位移和竖向位移均为0。除地基表面外,气体边界都为不排水边界。 4.1 地基沉降分析 红黏土地基固结分析中,通过分别定义初始孔隙比、初始有效应力和初始孔隙水压力得到地基在未建造建筑物前的初始应力场,形成地应力平衡状态。由图2可以看出,初始平衡状态地基土层表面处的最大竖向位移为2.22×10-17m,已达到应力平衡状态。 计算的基础下表面随时间沉降曲线如图3所示,从图中可以看出,有限元计算结果与土力学变化规律一样。从图3可以看出,经过1a地基的固结沉降量占总沉降量的50%,所用时间占总时间的10%,当到第5年的时候地基固结沉降量达90%,占总时间的50%,余下10%的沉降大约用了总时间的50%。 对图3中的基础下表面沉降-时间曲线进行拟合,得出基础下表面沉降随时间的规律符合ExpDec2模型,公式为 y=y0+A1e-x/t1+A2e-x/t2。 (5) 式中:y0,t1,A1,t2,A2均为常数,与土的性质有关。 图3 地表沉降-时间曲线Fig.3 Curves of settlement in earth surface vs. time 地基沉降拟合参数如表2所示。从图3中的拟合曲线和表2中的相关系数可以看出,拟合曲线与ABAQUS有限元计算的模拟曲线相关性很好,基础下表面的沉降规律可以用公式(5)进行描述。 表2 地基沉降拟合参数Table 2 Fitted parameters of foundation settlement 4.2 孔隙水压力分析 孔隙水压力是反映固结发展过程的一个重要指标。图4表明:孔隙水压力的衰减可分为2个阶段,即快速衰减阶段和缓慢衰减阶段。在上部建筑物荷载加载初期,土体中的水不能及时排除,产生超孔隙水压力,从图4可以看出,土层底部超孔隙水压力迅速增大到140 kPa左右。在快速衰减阶段,孔隙水压力消散了约80%的压力值,而所用时间为总时间的55%。在缓慢衰减阶段,孔隙水压力的消散时间占整个时间的45%左右,消散量却只占孔隙水压力的20%左右。随着土体固结时间的增长,超孔隙水压力慢慢消散,到第10 a,孔隙水压力基本全部消散。 对图4中的孔隙水压力消散曲线进行拟合,得出孔隙水压力的消散规律符合Gauss模型,公式为 (6) 式中:y0,xc,w,A均为常数,与土的性质有关。 孔压消散拟合参数如表3所示。从图4中的拟合曲线和表3中的相关系数可以看出,拟合曲线与有限元计算的模拟曲线相关性很好,孔隙水压力的消散规律可以用公式(6)进行描述。 图4 孔隙水压力消散曲线Fig.4 Curves of water pressure dissipation 表3 孔压消散拟合参数Table 3 Fitted parameters of pore waterpressure dissipation 4.3 孔隙比随深度变化 在实际工程中,土体的孔隙比并不是一个常数,而是随深度逐渐减小。在许多数值模拟中给出土体顶部和底部的孔隙比,而中间部位的数值则由这2个数值线性插值得到,即土体的孔隙比沿深度线性递减,但这种线性变化不符合实际工程情况。土体中孔隙比随深度增加而不断减小,但却不是线性递减,孔隙比数值的变化曲线近似于二次抛物线。因此编写了孔隙比随土体深度非线性分布的用户子程序VOIDRI,在模型的运算过程中使用这个子程序,主要是为了使模拟计算更加接近工程实际情况。 从图5中可以看到初始地应力平衡后,土体的孔隙比随深度的增加而非线性递减,这与工程实际情况一致。因此可以得到结论:在模拟的初始分析步中添加的子程序已经产生效果,使孔隙比的数值在随土体的深度变化上更加接近于工程实际情况,从而为模拟精度的进一步提高奠定了基础。 图5 孔隙比随深度分布曲线Fig.5 Curves of void ratio vs. depth 对图5中的孔隙比随深度递减曲线进行拟合,得出孔隙比随深度的递减规律符合ExpDec1模型,公式为 y=y0+A1e-x/t。 (7) 式中:y0,t,A1均为常数,与土的性质有关。 拟合参数如表4所示。从图5中的拟合曲线和表4中的相关系数可以看出,拟合曲线与有限元计算的模拟曲线相关性很好,孔隙比递减规律可以用公式(7)进行描述。 表4 孔隙比递减拟合参数Table 4 Fitted parameters of decrease in void ratio 图6 竖向有效应力随时间的变化Fig.6 Variation of vertical effective stress with time 4.4 有效应力随时间的增长规律 图6是初始应力平衡之后的竖向有效应力场随时间的变化,在土体底部,初始竖向有效应力为-90 kPa,经过10 a固结之后,土体的有效应力达到-227 kPa,增长了152%。在第4年左右时,土体的有效应力就达到了-185 kPa,增长了105%,土体有效应力增长了1倍所用的时间约40%,到第7年之后土体有效应力达到-220 kPa,增长了144%,后面3 a增长率越来越小,有效应力无太大变化。计算结果较好地反映了固结的本质,即有效应力随时间的增长而增加的过程。 对图6中的有效应力随时间的增长曲线进行拟合,用多项式拟合的效果较好,拟合公式为 y=0.020 5x5-0.570 8x4+5.630 4x3- 21.234x2+1.080 6x-89.848, R2=0.999 8 。 (8) (1) 对红黏土地基进行有限元分析,土体采用修正剑桥模型,经过10a固结,ABAQUS计算结果为32mm。得出基础下表面随时间沉降的规律符合ExpDec2模型,经过1a地基的固结沉降量占总沉降量的50%,所用时间占总时间的10%,最后10%的沉降大约用了50%的时间,这符合土力学的基本规律,表明了修正剑桥模型模拟红黏土是合理的。 (2) 地基经过1a固结的沉降量占总沉降量的50%,在第5a左右沉降量达到90%,随后的沉降是个缓慢的过程。 (3) 地基土体孔隙水压力消散规律可以用Gauss模型来描述,孔隙比随深度的变化规律可以用ExpDec1模型来描述。 (4) 地基土体的有效应力随着时间的发展是一个逐渐增长的过程,增长率越来越小,在第4a左右时,有效应力增长能达到1倍,在第7a左右,有效应力增长率几乎为0,能较好反映固结本质。 (5) 本文的工程实例分析表明,用ABAQUS自带的修正剑桥模型模拟红黏土固结是完全可行的,具有一定的合理性和实用性,可以应用于同类工程实际工程问题的分析。 [1] 李振明. 地基土随排水固结而强度增长在工程上的应用[J]. 工程勘察,1993,(3):13-17.(LIZhen-ming.ApplicationofSubsoilStrengthGrowthwithDrainageConsolidationinEngineering[J].GeotechnicalInvestigation,1993,(3):13-17.(inChinese)) [2]GB50007—2011,建筑地基基础设计规范[M]. 北京: 中国建筑工业出版社,2011. (GB50007—2011,CodeforDesignofBuildingFoundation[M].Beijing:ChinaArchitectureandBuildingPress,2011.(inChinese)) [3] 甘友文,王志亮,郑 华. 地基沉降预测中的双曲线模型修正[J]. 水文地质工程地质,2004,(1):98-100. (GANYou-wen,WANGZhi-liang,ZHENGHua.HyperbolicFoundationSettlementPredictionModelModification[J].HydrogeologyandEngineeringGeology,2004,(1):98-100. (inChinese)) [4] 杜海伟,张建军,李新生,等. 地基沉降计算指数曲线配合法及其应用[J]. 土工基础,2005,19(1):54-56.(DUHai-wei,ZHANGJian-jun,LIXin-sheng,etal. The Exponential Curve Fitting of the Calculation of the Subsoil Settlement Method and Its Application[J]. Soil Engineering and Foundation,2005,19(1):54-56. (in Chinese)) [5] 王志亮,黄景忠,李永池. 沉降预测中的Asaoka法应用研究[J]. 岩土力学,2006,27(11):2025-2028. (WANG Zhi-liang,HUANG Jing-zhong,LI Yong-chi. Study on Application of Asaoka’s Method to Settlement Prediction[J]. Rock and Soil Mechanics,2006,27(11):2025-2028. (in Chinese)) [6] 李秀珍,许 强,孔纪名,等. 九寨黄龙机场高填方地基沉降的数值模拟分析[J]. 岩石力学与工程学报,2005,24(12):2188-2193. (LI Xiu-zhen,XU Qiang,KONG Ji-ming,etal. Numerical Modeling Analysis of Settlements of High Fill Foundation for Jiuzai Huanglong Airport[J]. Chinese Journal of Rock Mechanics and Engineering,2005,24(12):2188-2193.( in Chinese)) [7] 郭志川,刘 宁. 地基固结沉降随机有限元计算和可靠度分析[J]. 岩土力学,2001,22(4):481-485. (GUO Zhi-chuan,LIU Ning. The SFEM Analysis and Reliability Assessment of Consolidation Settlement Based on Biot Consolidation Theory[J]. Rock and Soil Mechanics,2001,22(4):481-485. (in Chinese)) [8] 杨 坪,杨 军,许德鲜,等. 基于ADINA的软土坝基沉降分析[J]. 工程地质学报,2008,(4): 533-538.(YANG Ping,YANG Jun,XU De-xian,etal. Finite Element Analysis of Settlement of Soft Soil Foundation under Reservoir Dam[J]. Journal of Engineering Geology, 2008,(4): 533-538.(in Chinese)) [9] 费 康,张建伟. ABAQUS在岩土工程中的应用[M]. 北京: 中国水利水电出版社,2010. (FEI Kang,ZHANG Jian-wei. Application of ABAQUS in Geotechnical Engineering[M]. Beijing: China Water Power Press,2010.(in Chinese)) [10]王金昌,陈页开. ABAQUS在土木工程中的应用[M]. 杭州: 浙江大学出版社,2006. (WANG Jin-chang,CHEN Ye-kai. Application of ABAQUS in Civil Engineering[M]. Hangzhou:Zhejiang University Press,2006. (in Chinese)) [11]李广信. 高等土力学[M]. 北京: 清华大学出版社,2004.(LI Guang-xin. Advanced Soil Mechanics[M]. Beijing: Tsinghua University Press,2004.(in Chinese)) [12]龚晓南. 高等土力学[M]. 杭州: 浙江大学出版社,1996.(GONG Xiao-nan. Advanced Soil Mechanics[M]. Hangzhou:Zhejiang University Press,1996. (in Chinese)) [13]廖红建. 岩土工程数值分析[M]. 北京: 机械工业出版社,2009.(LIAO Hong-jian. Numerical Analysis of Geotechnical Engineering[M]. Beijing: China Machine Press,2009. (in Chinese)) [14]周葆春,王靖涛,杨晓东. 武汉黏土修正剑桥模型参数研究[J]. 武汉理工大学学报,2007,29(3):103-107. (ZHOU Bao-chun,WANG Jing-tao,YANG Xiao-dong. Research on Parameters of Modified Cambridge Model for Wuhan Clay[J]. Journal of Wuhan University of Technology,2007,29(3):103-107. (in Chinese)) [15]高 晖. ABAQUS在软基固结过程分析中的应用研究[D]. 武汉:武汉理工大学,2006. (GAO Hui. Study on Application of ABAQUS in Analysis during Consolidation of Soft Soil Foundation[D]. Wuhan:Wuhan University of Technology,2006.(in Chinese)) (编辑:黄 玲) Analysis on Drainage Consolidation Settlement ofRed Clay Foundation by Using ABAQUS ZHAO Lei1,CHEN Jun1, WU Zhong-hu1,LIU Lei-lei2 (1.College of Resource and Environmental Engineering,Guizhou University,Guiyang 550025, China;2.School of Geoscience and Info-Physics,Central South University,Changsha 410083, China) Due to the complexity of drainage consolidation of red clay foundation, we simulated and analyzed the consolidation settlement by using the consolidation calculation module Soils and modified Cambridge model of ABAQUS/Standard. The reconstruction project of an aluminum factory was taken as an example. The variation of red clay foundation’s settlement with time, the dissipation of pore water pressure, the non-linear distribution of void ratio with depth, and the effective stress growth of soil were researched. Results suggest that the calculated results are in good agreement with the law of soil mechanics, and the actual situation of the red clay foundation consolidation settlement could be reflected accurately. This research provides references for the foundation treatment and engineering design of buildings on red clay ground. red clay foundation;ABAQUS;modified cam-clay model;consolidation settlement;pore water pressure 2013-10-11; 2013-11-10 贵州大学2014年研究生创新基金项目(研理工2014019);贵州省地质灾害监测预警与决策支持平台建设项目(z113278) 赵 蕾(1990-),女,贵州贵阳人,硕士研究生,从事岩土力学性质及其应用方面的研究工作,(电话)0851-83621869(电子信箱)361193254@qq.com。 陈 筠(1970-),女,贵州贵阳人,副教授,硕士,主要从事区域稳定与岩体稳定、岩溶工程地质、地基与基础工程、边坡工程等方面的研究,(电话)0851-83621869(电子信箱)409272271@qq.com。 10.3969/j.issn.1001-5485.2015.02.021 TU446 A 1001-5485(2015)02-0103-05 2015,32(02):103-107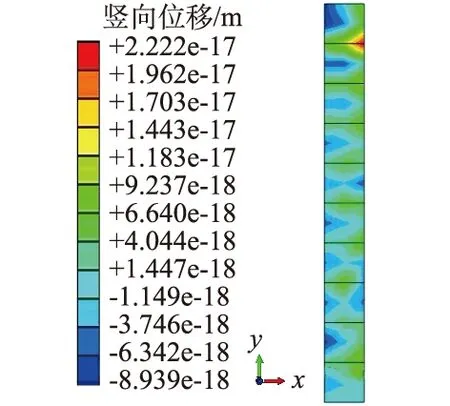
4 计算结果及分析





5 结 论

