向家坝导流底孔回填混凝土温度动态预测

周建兵，黄耀英，何小鹏，田开平

(1.中国长江三峡集团 向家坝工程建设部，四川 宜宾 644600;2.三峡大学 水利与环境学院，湖北 宜昌 423002)

向家坝导流底孔回填混凝土温度动态预测

周建兵1，黄耀英2，何小鹏1，田开平2

(1.中国长江三峡集团 向家坝工程建设部，四川 宜宾 644600;2.三峡大学 水利与环境学院，湖北 宜昌 423002)

导流底孔回填混凝土水泥含量高，温控难度大，一般需要埋设冷却水管进行通水冷却。针对导流底孔回填混凝土的特点，从动态预测角度出发，将有热源水管冷却计算式结合混凝土浇筑仓实测温度，根据浇筑仓当前实测温度动态更新有热源水管冷却计算式中的Ti，然后进行未来n天混凝土浇筑仓温度动态预测，以指导和调控现场通水措施。向家坝导流底孔回填混凝土温度动态预测的实例分析表明，建议的温度动态预测式是可行的。

导流底孔；回填混凝土；初期冷却；动态预测；向家坝水电站

1 研究背景

导流底孔混凝土回填一般施工工期紧，施工难度大[1]，其是影响电站蓄水和发电工期的关键节点。缩短底孔混凝土回填工期具有重要的工程意义。缩短工期可从优化施工工艺和优化温控措施2个方面进行。目前，对施工工艺的优化报道比较多[1-6]，而对温控措施的优化研究很少。对温控措施进行优化，必须要进行快速、准确的温度预测。对于混凝土水管冷却的温度计算，朱伯芳[7]假设等效冷却混凝土柱体的外表面为绝热边界，分别给出了无热源水管冷却计算式和有热源水管冷却计算式。针对中后期冷却期间混凝土浇筑仓顶面已覆盖浇筑若干层混凝土浇筑仓，而且浇筑仓侧面也已经粘贴保温苯板，为此，黄耀英等[8]建议采用无热源水管冷却问题的混凝土平均温度计算式，联合实测温度，对无热源水管冷却问题的混凝土平均温度计算式中的Ti进行动态更新，消除高掺粉煤灰缓慢放热以及上下游表面不是绝热边界等引起的误差，动态预测混凝土浇筑仓的降温过程线。对于一期冷却期间，混凝土存在水泥水化温升、以及混凝土新浇筑仓在间歇期间受外界环境气温影响很大等问题，导致直接采用有热源水管冷却计算式预测的精度较差。

导流底孔回填混凝土可归属于大体积混凝土范畴，其水泥含量高，温控难度大，一般需要埋设冷却水管进行通水冷却。对于混凝土新浇筑仓来说，3个面或5个面暴露在环境温度中，新浇筑仓内部的温度受环境温度影响很大。与混凝土新浇筑仓不同，对于导流底孔回填的混凝土来说，底孔周围为温度相对稳定的大体积混凝土，且底孔内环境气温也相对稳定，考虑到混凝土是热不良导体，底孔内环境气温对回填混凝土内部温度影响较小，即可以采用有热源水管冷却计算式，联合实测温度，较好地进行导流底孔回填混凝土的温度预测。为此，本文采用初冷有热源水管冷却温度预测式，结合向家坝导流底孔回填混凝土实测温度，进行导流底孔回填混凝土的温度动态预测。

2 初冷期间实时动态预测模型原理

2.1 初冷期间有热源水管冷却问题

对于导流底孔回填的混凝土来说，由于混凝土是热不良导体，可以假设导流底孔回填的混凝土处于近似绝热状态。此时，可采用初冷有热源水管冷却温度计算式。混凝土浇筑仓内埋设冷却水管进行通水冷却，设等效冷却水管直径为D，长度为L，有热源，混凝土初温为T0，进口水温为Tw，则混凝土平均温度可表示为[7]：

T(t)=Tw+(T0-Tw)φ(t)+θ0Ψ(t) ;

(1)

φ(t)=e-pt;

(2)

p=dka/D2;

(3)

k=2.09-1.35ξ+0.32ξ2;

(4)

(5)

d=1.947(α1b)2;

(6)

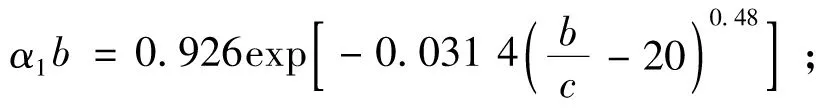
(7)

(8)

式中：t为冷却时间；a为导温系数；D,b,c分别为等效冷却柱体的直径、外半径、内半径；λ为混凝土的导热系数；s1,s2分别为水管水平和垂直向间距；Ψ(t)为与混凝土绝热温升有关的函数。

混凝土绝热温升表达式有指数型、双曲线型和复合指数型等。由于指数型绝热温升便于进行数学运算，为此，朱伯芳院士[7]给出了指数型绝热温升θ(τ)=θ0(1-emτ)下的Ψ(t)为

(9)

进一步分析表明，指数型绝热温升表达式与试验资料吻合得较差，为此，本文采用组合指数式绝热温升进行函数Ψ(t)的推导。

θ(τ)=θ0s(1-e-m1τ)+θ0(1-s)(1-e-m2τ) 。

(10)

式中：s=0.6；m1=1.45/n；m2=0.145/n。

设仅已知混凝土绝热温升试验值，则采用优化的方法来确定组合指数式中的m1,m2,s。

采用组合指数式绝热温升导出的函数Ψ(t)为

(11)

如果在一期冷却期间，采用多档水温进行通水冷却，则混凝土平均温度为

T(t)=Twi+(Ti-Twi)φi(t)+θ0Ψ(t) ;

(12)

φi(t)=e-pit。

(13)

绝热温升采用组合指数式，即

(14)

函数中的Twi为第i档通水温度；Ti为第i-1档水温通水结束且第i档水温开始通水时的混凝土温度；φi为第i档水温通水时的水冷函数；ti为改变水温或流量时刻，当改变水温或流量时时间t需要从0开始。

2.2 基于实测温度的初冷期间浇筑仓温度动态预测模式

由2.1节分析可知，有热源水管冷却计算公式隐含了等效冷却直径为D的混凝土柱体的外表面为绝热边界。虽然底孔周围为温度相对稳定的大体积混凝土，且底孔内环境气温也相对稳定，但对于底孔回填混凝土新浇筑仓来说，仍然一定程度受底孔内环境气温影响，这导致采用有热源水管冷却计算式的预测值与实测温度存在一定的差异。为此，从动态预测角度出发，将有热源水管冷却计算式和混凝土浇筑仓实测温度相结合，根据浇筑仓当前实测温度动态更新有热源水管冷却计算式中的Ti，然后进行未来n天混凝土浇筑仓温度动态预测，以指导和调控现场通水措施。有热源水管冷却问题的一期冷却期间混凝土浇筑仓温度预测如图1。

图1 一期冷却期间混凝土浇筑仓温度动态预测Fig.1 Dynamic temperature forecasting for concrete casting block in first stage cooling

由图1可见，基于浇筑仓当前实测温度动态更新有热源水管冷却计算式中的Ti，可以将浇筑仓层面散热边界等引起的误差，通过动态更新Ti来动态实时修正，从而克服有热源水管冷却计算式温度预测效果不理想的问题。

3 导流底孔回填混凝土绝热温升优化反演

由2.1节可知，混凝土绝热温升是初冷期间有热源水管冷却问题的重要组成部分，为此，本文采用初冷有热源水管冷却温度预测式并结合实测温度对混凝土绝热温升参数进行了优化反演。由式(10)可见组合指数式与双曲线式实际上是等价的，二者的参数可以相互转换，即可用上述方法反演最终绝热温升θ0和双曲线型绝热温升常数n。

对相同空间位置和相同时间上的温度实测值与计算值进行比较，使两者误差最小，可建立目标函数

(15)

使

F(X)→min。

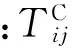
由于目标函数是设计变量的非线性函数，所以该优化模型属于无约束的非线性规划，采用单纯形法进行反演计算。单纯形法在N维空间的几何图形中有N+1个顶点，顶点之间用直线连接。再对各顶点的目标函数逐一进行比较，不断舍弃最坏点，代之以使目标函数值不断降低的新点。不断循环、迭代，直到目标函数满足给定条件时终止计算。本文采用Visual Fortran编制了单纯形法热学参数反分析程序。

4 实例分析

向家坝水电站是金沙江下游梯级开发中最末的一个梯级，坝址位于川滇两省交界的金沙江下游河段上，拦河大坝为混凝土重力坝，坝顶高程384 m，最大坝高162 m，水库正常蓄水位380 m，电站总装机容量为640万kW。左岸非溢流坝段和冲沙孔坝段共设6 个宽×高为10 m×14 m的导流底孔。选取典型导流底孔回填混凝土浇筑仓进行分析，首先基于初冷有热源水管冷却计算式，结合实测温度，采用单纯形法进行导流底孔回填混凝土绝热温升优化反演，然后基于优化反演参数进行导流底孔回填混凝土温度动态预测。

4.1 导流底孔回填混凝土绝热温升参数优化反演

典型仓混凝土位于导流底孔顶拱处，采用的是泵送自密实混凝土，强度等级为C25，混凝土配合比为水泥284 kg/m3,水170 kg/m3，粉煤灰94 kg/m3,砂率50%。其水泥含量比其他部位高，采用DN25铁管进行通水冷却，水管外直径为33.7 mm，水管间距为1 m×1 m(水平向×垂直向)，通水工况如表1。

表1 通水工况Table 1 Cases of water cooling load

基于初冷有热源水管冷却计算式，结合实测温度，采用单纯形法进行导流底孔回填混凝土绝热温升优化反演，反演结果为

θ(τ)=31.08(1-e-0.780τ)+20.72(1-e-0.078τ) 。

(16)

根据文献[7]中给出的绝热温升估算公式估算的最终绝热温升为54℃，由式(10)和式(16)可知，导流底孔回填混凝土优化反演的最终绝热温升为51.8℃，与组合指数型绝热温升等价的双曲线型绝热温升常数n为1.86 d。

4.2 导流底孔回填混凝土温度动态预测

基于优化反演的绝热温升，采用初冷有热源水管冷却温度预测式，按图1的动态预测模式，对典型仓0～28 d龄期混凝土温度进行了动态预测。具体参见通水工况表1，在通水水温和通水流量变化时的第3，11，14，21 d，结合实测温度对式(12)中的Ti进行动态修正。预测温度与实测温度对比如图2所示。

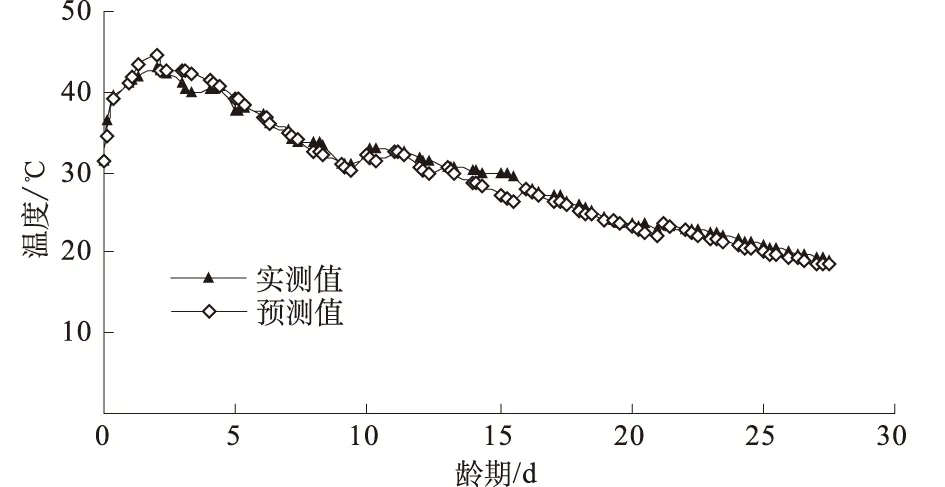
图2 基于反演参数的预测值与实测值对比Fig.2 Comparison between predicted temperature based on parameter inversion and measured temperature

由图2可见，基于优化反演绝热温升的计算温度与实测温度的吻合效果令人满意，这一方面说明绝热温升的反演结果是合理的，另一方面说明采用初冷有热源水管冷却温度动态预测方法可以很好进行导流底孔回填混凝土的温度预测。

5 结 论

本文采用初冷有热源水管冷却温度预测式结合向家坝导流底孔回填混凝土典型仓实测温度进行了绝热温升优化反演，并基于反演参数对典型仓0～28d龄期混凝土温度进行了动态预测，得到如下结论：

(1) 针对导流底孔回填混凝土的特点，从动态预测角度出发，建议将有热源水管冷却计算和混凝土浇筑仓实测温度相结合，基于浇筑仓当前实测温度动态更新有热源水管冷却计算式中的Ti，然后进行未来n天混凝土浇筑仓温度动态预测，以指导和调控现场通水措施。

(2) 根据典型仓混凝土实测温度，运用初冷有热源水管冷却温度预测和优化反分析方法，对自密实混凝土绝热温升进行了反演，优化反演结果与估算结果接近且计算值与实测值吻合效果很好，即绝热温升的反演结果是合理的。

(3) 基于优化反演参数对典型仓混凝土0～28 d龄期进行了动态预测，预测值与实测值吻合得较好，即采用初冷有热源水管冷却温度动态预测方法，可以很好地进行导流底孔回填混凝土的温度预测。

[1] 何小鹏,许光明,王忠民,等.三峡工程导流底孔封堵生产性试验研究[J].人民长江, 2006,37(5):15-18.(HE Xiao-peng, XU Guang-ming, WANG Zhong-ming,etal. Full-scale Experimental Study of Plugging Construction of Bottom Diversion Outlet of TGP[J]. Yangtze River, 2006, 37(5):15-18. (in Chinese))

[2] 杨秀彬.小湾水电站导流底孔封堵混凝土施工[J].水利水电施工, 2012,(5):15-17.(YANG Xiu-bin. Plugging Construction of Bottom Diversion Outlet of Xiaowan Hydropower Station[J]. Construction of Hydraulic Engineering, 2012, (5):15-17. (in Chinese))

[3] 林毅辉.蒙州水电站拦河坝施工导流设计及导流底孔封堵施工方法的探讨[J].小水电, 2005, (5):66-67. (LIN Yi-hui. Discussion of Construction Diversion Design and Plugging Construction Method of Bottom Diversion Outlet of Mengzhou Hydropower Station Dam[J]. Small Hydro Power, 2005, (5):66-67. (in Chinese))

[4] 肖汉江,崔建华,李祖民,等.三峡大坝导流底孔封堵温度应力仿真计算分析[J].长江科学院院报, 2002,19(6):17-20.(XIAO Han-jiang, CUI Jian-hua, LI Zu-ming,etal. Thermal Stress Emulational Calculation on Blockage Body of Bottom Outlet of Spillway Dam Section for TGP[J]. Journal of Yangtze River Scientific Research Institute, 2002, 19(6):17-20.(in Chinese))

[5] 王尚海,陈剑红.隔河岩大坝导流底孔封堵的施工[J].湖北水力发电, 2003, (4):19-21. (WANG Shang-hai, CHEN Jian-hong. Plugging Construction of Bottom Diversion Outlet of Geheyan Dam[J]. Hubei Water Power, 2003, (4):19-21. (in Chinese))

[6] 李 然.小湾水电工程坝身导流底孔封堵施工技术[J].水利水电技术, 2012,43(3):42-46.(LI Ran. Construction Technology for Plugging of Diversion Bottom Outlet of Dam for Xiaowan Hydropower Project[J]. Water Resources and Hydropower Engineering, 2012, 43(3):42-46. (in Chinese))[7] 朱伯芳.大体积混凝土温度应力与温度控制[M].北京:中国电力出版社,1999.(ZHU Bo-fang. Thermal Stresses and Temperature Control of Mass Concrete[M]. Beijing: China Electric Power Press, 1999. (in Chinese))

[8] 黄耀英,周绍武,付学奎,等.中后期冷却期间混凝土浇筑仓温度动态预测模型[J].四川大学学报(工程科学版), 2013,45(4):34-38.(HUANG Yao-ying, ZHOU Shao-wu, FU Xue-kui,etal. Dynamic Forecasting Model of Concrete Casting Warehouse in Middle-late Cooling Age[J]. Journal of Sichuan University (Engineering Science Edition), 2013, 45(4):34-38. (in Chinese))

[9] 朱伯芳.混凝土热学力学性能随龄期变化的组合指数公式[J].水利学报,2011,42(1):1-7.(ZHU Bo-fang. Compound Exponential Formula for Variation of Thermal and Mechanical Properties with Age of Concrete [J]. Journal of Hydraulic Engineering, 2011, 42(1):1-7. (in Chinese))

(编辑：曾小汉)

Dynamic Prediction of Concrete Temperature for the Plugging ofBottom Diversion Outlet of Xiangjiaba Hydropower Project

ZHOU Jian-bing1, HUANG Yao-ying2, HE Xiao-peng1, TIAN Kai-ping2

(1.Xiangjiaba Project Construction Department, Three Gorges Corporation, Yibin 644600, China;2.College of Hydraulic and Environmental Engineering, Three Gorges University, Yichang 443002, China)

The concrete plugging of bottom diversion outlet has high proportion of cement, posing big challenge to the temperature control, therefore pipe cooling is needed. In this research, we recommend to combine the heat pipe cooling calculation formula with the measured temperature of concrete block, which means to dynamically updateTiin the heat pipe cooling calculation formula according to the measured temperature, and then predict the dynamic temperature of concrete block ofndays in the future to guide and control the pipe cooling. The dynamic prediction for concrete temperature is proved to be feasible by the practical example of concrete temperature of plugging of bottom diversion outlet at Xiangjiaba Hydropower Project.

bottom diversion outlet; plugging concrete; initial pipe cooling; dynamic prediction;Xiangjiaba hydropower station

2013-09-24；

2013-11-24

国家自然科学基金项目(51209124)

周建兵(1985- )，男，湖北武汉人，工程师，硕士，主要从事水利工程项目管理工作，(电话)18608319350(电子信箱)zhoujianbing309@163.com。

10.3969/j.issn.1001-5485.2015.02.024

TV544;TV431

A

1001-5485(2015)02-0119-04

2015,32(02):119-122