用于无线传感器网络的节点间协同定位算法的设计*

王 明,孟 赟,李 竞,应可珍,陈庆章

(1.宁波大红鹰学院信息工程学院,浙江 宁波 315175;2.杭州华三通信技术有限公司,杭州 310053;3.浙江工业大学计算机学院,杭州 310023;4.浙江财经大学东方学院,浙江 海宁 314408)



用于无线传感器网络的节点间协同定位算法的设计*

王 明1,孟 赟1,李 竞2,应可珍3,4,陈庆章3*

(1.宁波大红鹰学院信息工程学院,浙江 宁波 315175;2.杭州华三通信技术有限公司,杭州 310053;3.浙江工业大学计算机学院,杭州 310023;4.浙江财经大学东方学院,浙江 海宁 314408)

给出一种无线传感器网络中无锚节点情况下的节点间相互协同定位的算法。它首先将节点进行分簇,把角度测量和距离测量结合起来,通过方位协同,逐步对同步中的节点进行方位调整和坐标调整,从而计算出所有节点的相对坐标。仿真结果表明,在节点随机分布的情况下,该算法比起业界公认的聚类SPA算法在网络覆盖率、定位误差率和通信开销3个方面都有更好的表现。

无线传感器网络;协同定位算法;无锚节点定位;节点分簇

无线传感器网络WSN(Wireless Sensor Network)是大量的静止或移动的传感器以自组织和多跳的方式构成的无线网络,目的是协作地探测、处理和传输网络覆盖区域内感知对象的监测信息,并报告给用户。无线传感器网络被列为2l世纪最有影响的21项技术和改变世界的10大技术之一[1-2]。网络中的节点通常被随机布置在不同的环境中以实现各种监测工作,监测数据有效性与节点所处位置密切相关。因此,用以确定节点位置的节点定位技术是无线传感器网络研究的重点之一。

目前常见的节点定位方法是在所布属的节点中,设置部分具有全球卫星定位系统GPS(Global Positioning System)功能的节点,我们称之为锚节点(beacon node),其他节点的位置则根据锚节点来进行计算。但实际应用中,因为各种原因常常无法设置锚节点,此时的节点定位就必须实现节点之间协同工作的相对定位,也称节点自定位或节点协同定位。这种无锚节点的协同定位算法,其原理是通过无线传感网络内部节点间的相互测距和信息交换,得出节点的相对位置。此类算法虽然无法与基于锚节点定位算法一样可以测出节点的绝对位置信息,其所得到的相对位置信息足可以应用在对象监测、同步、尤其是基于地理位置的路由(geo-routing)[3]等应用上。并且如果以后能够取得3组以上的实体坐标系位置信息时,便可轻易将该相对坐标系统转换为绝对坐标系统,增进了使用上的弹性与便利性。

本文提出的无锚节点的协同定位算法,结合了角度测量和距离测量,通过方位协同逐步对同步中的节点进行方位调整,从而计算出所有节点在区域坐标系统当中的坐标。

1 相关研究

目前关于无锚节点定位算法的研究得到了高度重视,并推出很多研究成果。Motomura S等提出的无锚节点的定位方法,它只需要局部传感器节点的协同交互来确定传感器节点的位置,该方法利用链路质量指示器LQI(Link Quality Indicator)和节点间的跳数进行测量[4]。Chen Yuan-Fang等提出了一种不需要依赖GPS支持的锚节点的室内定位算法,该算法利用一个移动节点,使其在部署区域内沿着特定的轨迹移动并根据起始坐标和移动信息计算实时坐标[5]。傅贤锋等引入锚节点定位算法中共线度的概念,提出一种基于超声波四元阵测距的无锚节点定位算法[6]。Emokpae L等介绍了一种基于表面的反射模型,利用同态反褶积技术建立水表面反射通信链路,在此基础上建立一种可以用于独立节点建立相对坐标系的基于表面的反射无锚节点定位算法[7]。此外,也有结合两者优点开展的研究,如利用多维标度技术MDS(Multidimensional Scaling),采用少量锚节点实现网络定位的MDS-MAP算法[8],并且刘健苗等在此基础上引入Euclidean距离估算思想构建距离矩阵,并优化了最小二乘逼近的坐标转换方法对MDS-MAP算法进行了改进,获得了较好的效果[9]。

分析已经推出的研究成果,比较典型的无锚节点定位算法还是SPA(Self-Positioning Algorithm)[10]、聚类SPA[11]和MAP-Growing[12]3种。在SPA算法中,网络中每一个节点首先选取两个邻居节点建立该节点自身的坐标系统与坐标轴方向,再利用三边定位法,向外推算出其他节点的对应位置。再利用此方法构建其他节点的坐标系。之后再选定其中一个或一群节点作为坐标原点,通过节点合并建立一个整体的坐标系。在此算法中,由于每个节点都需要参与多次的坐标转换,算法的通信开销非常大。由于此算法针对无线自组织网络提出的,不需考虑能耗情况,若移植到无线传感器网络中,这种算法便不适合。为了提高上述SPA算法的扩展性,以及改进通信量过大的问题,Iyengar R等提出了聚类SPA算法。此算法首次引入了聚类思想,加入了分簇阶段,使算法整体的时间、通信开销减少,但存在后期冗余通信多、网络覆盖率不高的问题。Map-Growing算法是一种基于测距的算法,由Missouri-Columbia大学的Xiaoli Li等提出。其基本思想是构建3个内角都大于30°的良好三角形,并采用递归算法,重复地进行三边定位,从而获取节点坐标,最后再转换为全局绝对坐标。该算法实现简单、拓扑结构要求低,但存在累计误差现象,算法收敛速度慢。

针对以上现状,本文在SPA算法的基础上,提出了无锚节点的协同定位算法即CCPA算法(Clustering-based and Collaborative Positioning Algorithm In Anchor-free),该算法对节点进行聚类分簇。与Iyengar r等人提出的聚类SPA算法相比,CCPA算法在性能上将得到明显的提升。

2 无锚节点的协同式定位算法设计

2.1 算法思想

与聚类SPA算法类似,CCPA算法也分为分簇、建立局部坐标和建立全局坐标3个阶段。但聚类SPA算法存在分簇不均匀、簇间交集大、部分节点无法找到合适的邻居节点计算坐标以及因边界节点不足无法转换到全局坐标等问题。为了解决这些不足,CCPA算法在分簇和定位方面采取了不同的方式:

①簇形成阶段:先将网络初始化,在基于节点密度的分簇算法CAND(Clustering Algorithm based on Node Density)[13-14]的基础上,使用改进后的基于节点密度的分簇算法ICAND(Improved CAND)进行分簇,选出主节点,以主节点为中心的周围一跳邻居为从节点,将整个网络分为带有交叉区域的各个簇,把各节点分成3类:主节点、从节点和边界节点。其中边界节点定义为从属于i节点簇(甚至可能是主节点i自身)同时能收听到其他簇节点(主节点或从节点都行)的节点,而聚类SPA算法将边界节点定义为从属于i节点簇同时又能收听到其他簇的主节点的节点,相比而言本算法对边界节点的定义更宽泛。

②簇内同步阶段:节点通过多个超声波接收机或天线阵列感知发射节点信号的到达方向,从而测得对应的相对方位或角度,利用角度测量数据实现簇内节点的方位同步。方向是从节点同步到主节点,主节点依此以自身为坐标原点建立局部坐标系,通过上个阶段所得的角度和距离信息,利用本文推导出的公式计算出各从节点在所属局部坐标系的坐标值。

③全局协同阶段:首先是与全局中心簇相邻的簇的主节点通过与边界节点交换数据包,在此仅需一个边界节点即可完成两簇间的合并,计算出本局部坐标系同步到全局坐标系的相应信息,先实现全局节点的方位同步,再实现距离同步,同步至全局坐标系;与已同步簇相邻的簇同样依此方法同步到全局坐标系,如此重复以全局簇为中心向外同步,直至所有簇都同步到全局坐标系,从而实现节点的自定位。

为了获得节点间的距离信息以及建立坐标系,CCPA算法使用了5种不同的消息类型来进行节点内部通信。每个消息类型包括发送端节点ID(NodeID)、主节点ID(MasterID)、消息类型、消息体(Body)4部分内容。5种消息类型的组成如下:

①DISTANCE[NodeID,MasterID,Distance,Body]:让邻居节点获得与发送节点之间的距离信息。在基于测距的定位中,需要测得相邻节点间的距离或角度,目前的主流技术包括RSSI、AOA、TOA、TAOA等[15]。其中的TOA(Time of Arrival)[16]算法根据到达时间来实现节点间距离的测算,其具有成本低的优点。本算法采用TOA方法来测距,因而Body中的内容是发送节点在发送本消息时的时间戳。

②ANGLESYNC[NodeID,MasterID,AngleSync,Body]:本消息用于簇内同步阶段的角度同步,Body包含的是同步的轮次和主节点测量出从节点相对于自身坐标所在的角度值。

③CENTER[NodeID,MasterID,Center,Body]:本消息用于全局协同阶段。用来选取全局坐标系统的原点,Body中包含的是主节点的连通度。

④BORDER[NodeID,MasterID,Border,Body]:本消息用于全局协同阶段。由边界节点发送给邻居簇的主节点或从节点。Body中包括数组{nodeID,Angle,coordinates1,coordinates2}。nodeID是邻居节点的ID号,Angle是此边界节点测量得相对于nodeID节点的相对方向角,coordinates1是此边界节点在主簇的局部坐标值,coordinates2是此边界节点在以nodeID节点为坐标原点的坐标系中的局部坐标值。

⑤MERGE[NodeID,MasterID,Merge,Body]:本消息用于全局协同阶段。Body中包括的是需逆时针调整的角度和发送节点在全局坐标系中的坐标值。

2.2 簇形成

高效的分簇算法是提高定位算法效率的关键。这里采用的ICAND算法通过降低簇与簇之间的重叠度和对生成簇大小的限制来提高分簇效率。具体分为4阶段:

①网络初始化阶段。节点广播自身ID、当前获得的邻居节点的数目和ID。邻居节点收到消息后,更新自己的邻节点信息表,里面储存着所有的一跳邻节点的ID、此节点到本节点的距离、其邻节点数目、所入簇的数量以及所属簇ID列表共5项,并根据其邻节点数目的大小通过选择排序算法进行排序。

②成簇阶段。各节点设置一个随机定时器,时间一到,便比较自己和所有的一跳邻居节点的连通度,具有最大连通度的那个节点被选取为主节点。然后,当选的主节点判断自己的连通度是否大于网络预先设定的阈值T。连通度如果大于T,则搜索自身邻节点信息表中T个拥有最少邻节点数目的节点发布RECRUIT消息,否则,广播RECRUIT消息给邻节点信息表中的所有节点。收到RECRUIT消息的节点入簇,记录下主节点ID号,成为从节点,如果已经入别的簇,同样入该簇,成为边界节点。通知邻居节点,并更新自己的邻节点信息表。在此处,已选择了主节点的节点称为“covered node”,不再参与主节点的选取。还未选择主节点的节点称为“uncovered node”。

③迁移阶段。主节点计算本簇的冗余度,即边界节点的数目与簇内节点总数的比值。令冗余度阈值为50%。如果冗余度超过阈值,则主节点准备迁移。主节点从邻节点信息表中选取密度即连通度最大的从节点作为候选节点,把主节点的位置让贤给此候选节点。首先通知邻居节点自己成为了普通节点,而候选节点成为了新的主节点。收到此消息的节点,如果为候选节点,则改变自身的状态为簇头,发布RECRUIT消息;如果为旧主节点与新主节点的公共节点,则更新邻节点信息表,更换所属主节点的ID;如果为旧主节点成员而非新主节点的邻居,则更新邻节点信息表,把自身状态改为“uncovered”,完成簇的迁移阶段。

④结束阶段。当前两个阶段结束以后,可能有少量节点还在“uncovered”状态,所以最后需要再进行一次“clean-up”即清理过程,该过程不再进行簇的迁移,其自举成为簇头,发布RECRUIT消息,这样可以保证每个节点都属于一个簇或多个簇。至此整个ICAND算法结束。

2.3 簇内协同

簇内协同是指簇内的方位协同,通过调整簇内从节点的坐标轴方位来实现。在初始条件下,由于节点的随机部署,每个节点都有一个自身认知的Y轴正方位(正北方向),并以自身为坐标原点自行定义一个坐标系,导致各个节点所定义的坐标系的方位与角度都并不一致。因此需要将簇内从节点的坐标轴方位调整为统一的Y轴正方位,并以主节点为坐标原点建立局部坐标系,从节点计算并更新自己的新坐标。

2.3.1 收发节点间方向角的计算

簇内协同需要计算节点间的方向角,每个节点通过内置的超声波接收机或天线阵列来感知信号的到达方向并计算。图1展示了节点A配两个接收设备R1,R2的结构图。R1,R2分别位于节点A的两侧等距离处,距离相隔L。节点A自身认知的坐标系统的Y轴即为R1,R2连线的中垂线,X轴即为R1,R2的连线。R1,R2接收到发送节点B发射过来的信号后,通过TOA技术测量出节点B分别到R1,R2的距离X1,X2,根据几何关系,便可以计算出节点B在节点A自身认知的坐标系统中的方向角θ。若实际运用中有多个超声波接收设备或天线阵列,角度计算仍按上述方法。

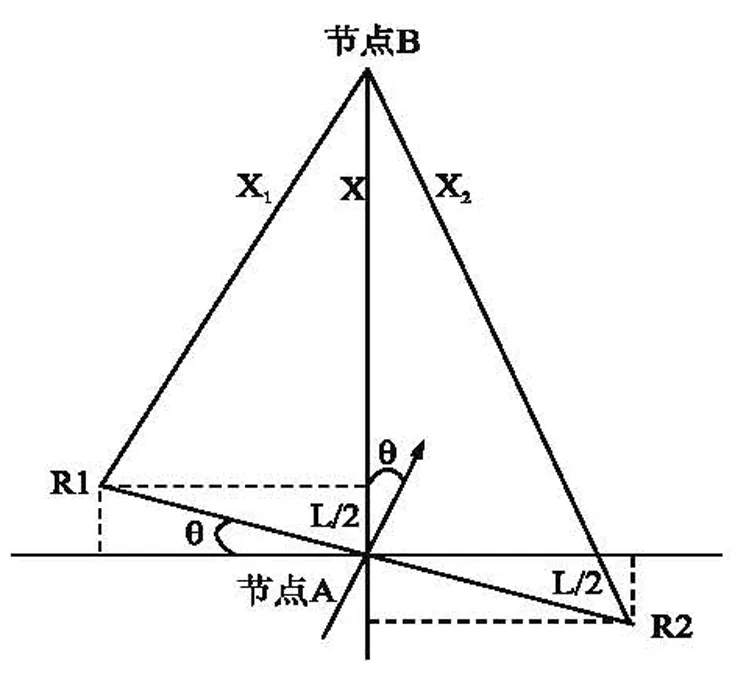
图1 节点结构图

2.3.2 簇内协同

簇内协同由主节点触发,主节点周期性地广播消息ANGLESYNC给它的从节点。从节点根据存储的主节点ID号接收协同信息,非主节点的协同信息将被抛弃。如图2所示,在ANGLESYNC信息中包含角度参数,各个从节点根据该参数并发地进行角度协同。

图2 簇内角度协同开始

图2中,A为主节点,B,C等为从节点。利用角度测量,可得从节点B相对于主节点A的角度WAB以及主节点A相对于从节点B的角度WBA。则从节点B的调整方式按式(1)方式进行:

(1)

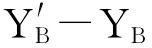
对于两个协同周期内都未收到协同消息的从节点,该节点就认为其主节点处于失效状态,它将接收来自其邻居节点的协同消息,并比较协同轮次的大小。如果邻居节点协同信息包的协同轮次新于自己的协同轮次,它就将自己的方位同步到此邻居节点的方位,从而达到簇内方位的协同。

2.3.3 簇内局部坐标构建

簇内各节点方位协同之后,即可构建簇内局部坐标。如图3所示,主节点以自身为原点建立局部坐标系,于是主节点A的坐标为(0,0)。所有节点的自我认知坐标点初始化也都为(0,0)。dist(A,B)为节点A所测量到的与节点B的距离,由此可得式(2):

(2)

B′:(XB,YB)即为更新后的子节点坐标。其余从节点也依方法更新自己的局部坐标值。

图3 簇内局部坐标系构成

2.4 全局协同

在全局坐标系构建的过程中,通过合并簇并转换节点坐标来实现。本算法从数量少的节点簇逐步向数量多的节点簇转换,初始时每个主节点把自己作为网络的中心,向外广播一条CENTER消息,在主节点间转发,从而选举度数最大的节点作为网络的中心。

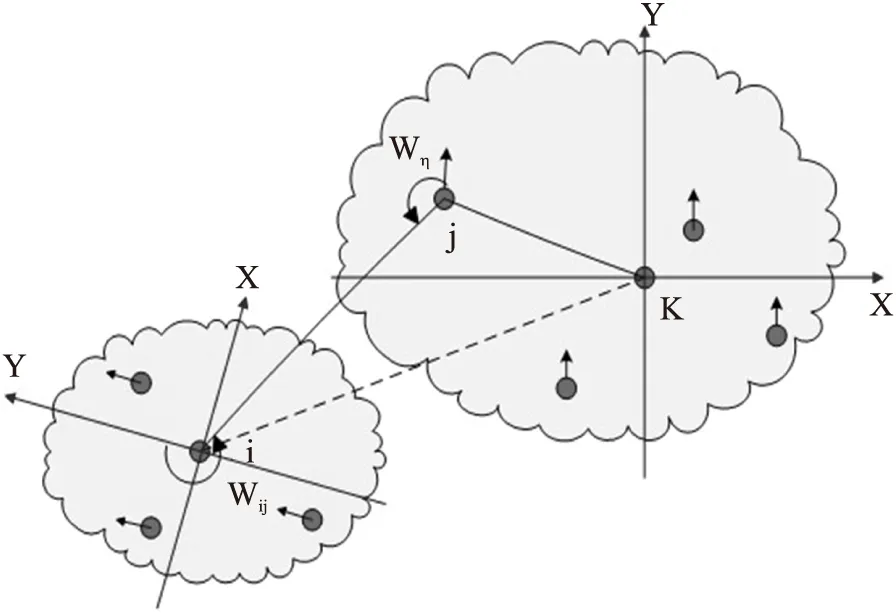
图4 可连通节点簇簇间方位协同前

2.4.1 两类节点簇

在全局协同时,根据簇头节点能否和邻居簇中已定位的边界节点连通将节点簇分为可连通的和不连通的两类。两类节点簇的簇间方位协同前的示意图如图4和图5所示。其中k簇是已定位的全局簇,i簇是未定位的节点簇,需要从i簇向k簇进行转换。在图5中,节点m和节点j分别属于i节点簇和主簇k并无法与其他簇主节点保持连通,但节点m和节点j之间能通信。

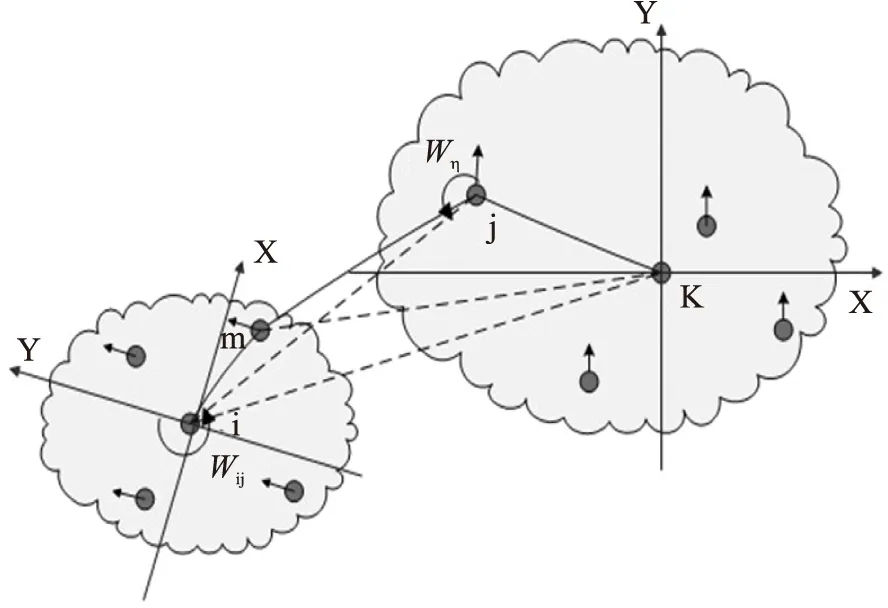
图5 不可连通节点簇簇间方位协同前

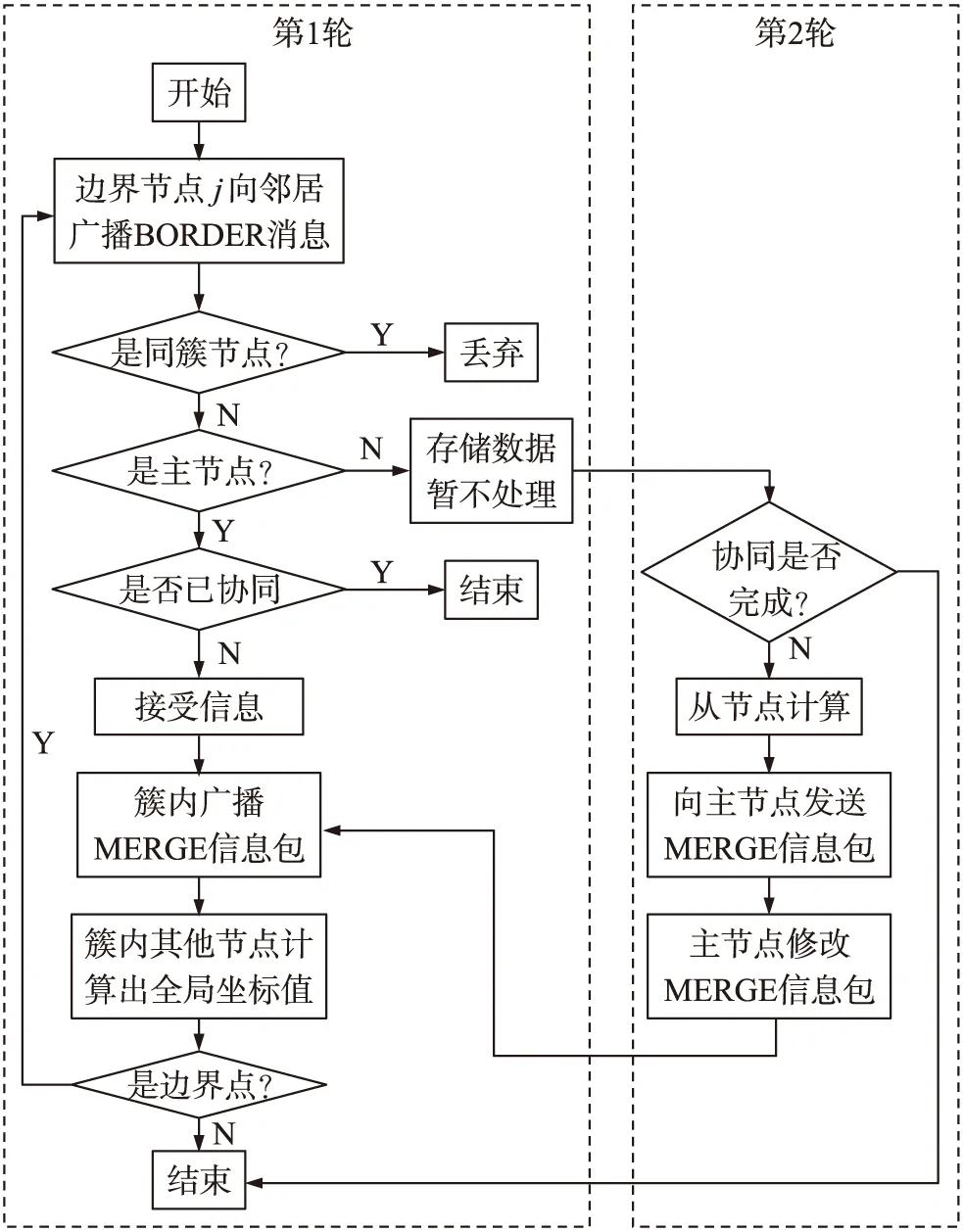
图6 节点簇的簇间协同流程

2.4.2 簇间协同

两类节点簇的簇间协同流程如图6所示,主要涉及两轮协同操作。第1轮协同操作针对可连通节点簇,未同步的主节点需接收BORDER消息并计算出坐标变换所需信息(RA,ki),其中RA为方位需逆时针调整的角度,ki为主节点在全局坐标系中的坐标值(坐标均用向量表示)。之后在簇内广播MERGE信息包,信息包中Body内包含的需逆时针调整的角度即是RA,主节点在全局坐标系中的坐标值即是ki。簇内所有节点根据此信息实现全局的方位协同,并计算出自身的全局坐标值,实现定位的节点簇加入集合S(1)。此时,如果簇内接收到MERGE信息的为边界节点,则在计算自身的全局坐标值之后再广播BORDER消息包,重复上述过程,直至所有符合要求的局部坐标系全部协同至全局坐标系。

若上一轮全局协同完成后,节点簇还未同步到全局节点簇,则启动第2轮全局协同,此时操作的是不可连通的节点簇。在第1轮全局协同时,部分簇的从节点m储存了相关信息暂时没处理。在此轮协同阶段中,图5中的节点m计算出坐标变换所需信息(RA,km),km为节点m在全局坐标系中的坐标值。而后节点m向它的主节点i发送一个MERGE信息包,信息包中包含了(RA,km)信息。主节点i收到MERGE信息包后,将信息包中的发送节点在全局坐标系中的坐标修改成ki,然后在簇内广播此MERGE信息包,之后的过程如同第1轮中的后续过程。同样,实现定位的节点簇加入集合S(1)。

以上全局协同的方法完全是分布式进行的,以DISTANCE,ANGLESYNC,CENTER,BORDER,MERGE等消息驱动,各个节点根据收到的不同消息做出不同的响应动作,每个节点都有自己的周期。

2.4.3 全局坐标值的计算

①计算(RA,ki)和(RA,km)

(RA,ki)和(RA,km)的计算方法一致,此处仅说明(RA,ki)的计算。通过对BORDER信息包的Body中nodeID的查找,可发现跟自身ID一致的nodeID,对应的Angle字段即为边界节点j监测的主节点i的相对方向角Wji,同时主节点i可以监测得边界节点j的相对方向角Wij,可以得出式(3):

RA=[Wij-(Wji-π)]

(3)

式中:RA为方位需逆时针调整的角度,Wij与Wji的范围为0～2π。

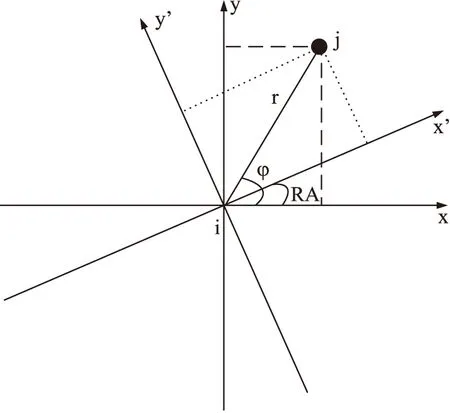
图7 局部坐标系调整方位后边界节点重新计算坐标

由平面坐标和极坐标之间的关系可表示为:

(4)

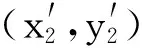
(5)

随后,因为节点i和节点k的局部坐标值都为(0,0),通过如下公式可得式(6):

(6)

②簇内从节点坐标值转换为全局坐标值

从节点根据主节点发来的MERGE信息包计算自己的全局坐标值。在主节点调整了自己的局部坐标值后,从节点的局部坐标值也需要调整,假设m是从属于i的一个从节点,调整之前m的坐标是(x,y),调整之后m的坐标是(x′,y′)。同理,根据(x′,y′)与(x,y)之间的关系,可得调整之后m的坐标如式(7)所示:

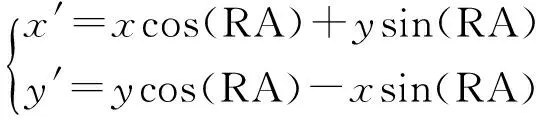
(7)

3 仿真实验与分析

所有的实验环境均在二维环境下所完成,利用MATLAB中的交互式的高级编程语言—M语言完成所有的仿真实验,为方便比较,实验采用的参数与聚类SPA一致:地域范围分别30 m×30 m,节点随机分布于这个方形区域中,通信半径为2 m。

3.1 网络覆盖率的比较

评价一个定位算法性能的重要方面就是看能不能实现网络中绝大部分节点的定位,即网络节点覆盖率的大小。网络覆盖率定义为Cov=(N/M)×100%,其中M表示全网络中传感器节点总数,N表示定位结束后能够获得位置坐标的传感器节点总数。本文所提出的CCPA算法便将网络覆盖率作为最主要改进的指标进行研究,无论是通过使用方位角信息,还是在全局协同阶段改进两簇合并的条件,都是为了提高网络覆盖率。下面对比两种算法在低节点密度区域的性能对比,其中节点密度定义为每平方米的节点个数。

分析图8可知,聚类SPA和本算法的网络覆盖率大体上都与节点密度成正比。聚类SPA算法的节点覆概率在不同节点密度下平均为35%,其中节点密度为0.28时具有最高的网络覆盖率为32%,而在节点密度为0.1时其覆盖率仅为18%。而CCPA算法的平均覆盖率为70%,其中节点密度为0.26时其覆盖率最高约为84%,而最低的网络覆盖率也有39%。在相同节点密度下,相对于聚类SPA算法,CCPA算法的网络覆盖率提升接近一倍。聚类SPA算法在低节点密度的情形下网络覆盖率不高的主要原因是在建立局部坐标系阶段,会出现大量节点无法找到除簇头以外的两个已获取局部坐标的邻居节点来实现定位,从而无法获得自身局部坐标值而导致节点失效,再加上全局协同阶段没有两个以上的边界节点导致出现更多的失效节点,而CCPA算法采用距离加角度信息,使两簇协同的条件放宽了很多,两方面共同作用使得CCPA算法在低节点密度的场景下网络覆盖率也有一个良好的表现。

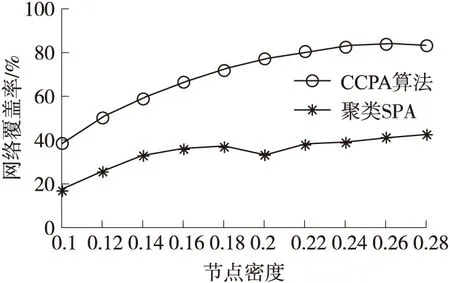
图8 网络覆盖率的比较

3.2 定位误差率的比较

接下来对算法定位误差率进行考察,定位误差率也是定位算法主要考虑的方面,定位误差主要来源于距离测量误差、角度测量误差以及算法计算过程中的误差累计问题。定位误差率定义为式(8):

(8)

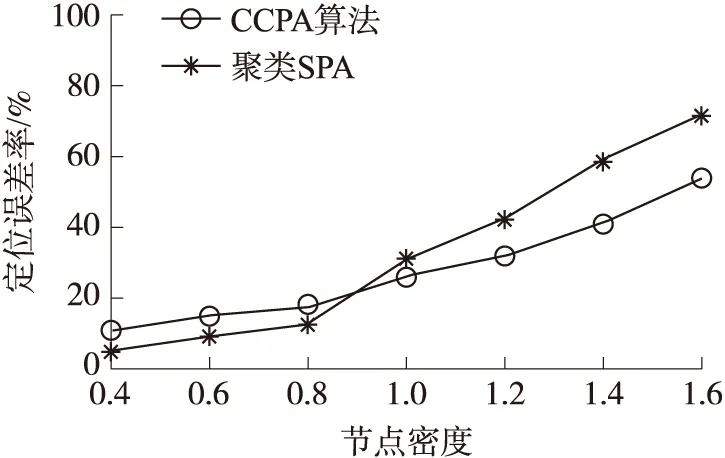
图9 定位误差率的比较

从图9可以得出,两个算法的定位误差率都与节点密度成正比,两条曲线都随着节点密度的上升而上升。聚类SPA算法比CCPA算法上升速度要快,坡度更明显。在节点密度小于一定程度的时候,聚类SPA算法的定位误差率比CCPA算法要小。但在节点密度大于0.9以后,CCPA算法的定位误差率变得比聚类SPA要小,其平均定位误差率比聚类SPA算法减少了22.3%。产生这个现象的主要原因是聚类SPA在节点密度较低的时候网络覆盖率也比较低,能实现定位的这些为数不多的节点主要是位于全局中心簇附近的节点簇,其坐标的转换次数少,导致误差累积比较小;而CCPA在节点密度较低的时候网络覆盖率也比较高,离中心节点簇较远的节点簇也能实现定位,但误差累积相对来说比较大,因此总体上看来,在节点密度比较小的时候聚类SPA算法的定位误差率比CCPA算法要小。然后,随着节点密度的逐渐增大,聚类SPA也会受到离全局中心簇比较远的节点的误差累积的影响,而且影响的比重会逐渐加大。所以在节点密度较高的时候,CCPA算法的定位误差率会变得比聚类SPA要小,并且差距会越来越明显,本算法的优势会逐渐显现。

定位误差率会随着节点密度的增长而变大。这是因为在全局协同阶段会产生误差叠加现象。误差叠加现象指的是,由于距离测量误差和角度测量误差的存在而导致节点计算自身全局坐标值时会产生一定误差,而其他未同步簇又会根据这已有一定误差的坐标值计算自身的坐标,从而导致误差叠加现象。因此可以推出,节点簇参与坐标转换计算的次数越多,误差累积越严重。在分簇阶段CCPA算法比聚类SPA算法形成的簇的数量要少,另外在全局协同阶段的全局协同策略的不同,两方面的共同作用使得CCPA算法比聚类SPA算法减少了很多的坐标转换次数,因此定位误差率方面表现更好。但是由于CCPA算法比聚类SPA算法多了个角度测量误差,两者中和,因此改进不是特别明显。

3.3 通信开销的比较

在不同节点密度值下本算法和聚类SPA算法的通信量及其差距对比如图10所示。从图中可以看出,两算法的通信量随节点密度的上升呈线性增长。那是因为两算法在簇形成阶段与簇内同步阶段都需要收集节点信息,节点数越多,所需的通信量越大。但聚类SPA增加的速度比本算法速度快。并且,在节点密度加剧的时候,这种差异更明显。

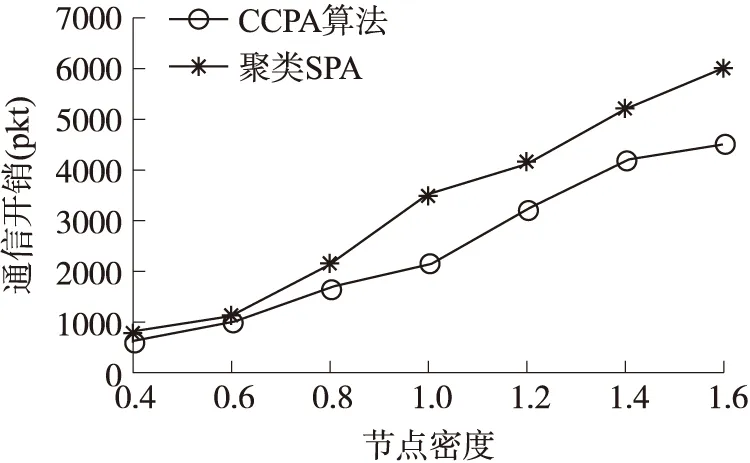
图10 通信开销的比较

4 总结

本文提出了一种无锚节点的无线传感器网络协同定位算法:CCPA算法。在无锚节点存在的情况下,利用改进后的基于节点密度的分簇算法,即ICAND算法进行分簇,通过分布式的定位方式,把角度测量和距离测量结合起来,逐步对同步中的节点进行方位调整和坐标调整,从而计算出所有节点在区域坐标系统当中的坐标。仿真实验数据表明,在节点随机分布的情况下,CCPA算法在网络覆盖率、定位误差率和通信开销方面都有良好的表现,比起业界公认的聚类SPA算法,网络覆盖率提高了接近一倍;另外,在节点密度大于0.9时,其定位误差率平均减少了22.3%。

[1] Byrne J A. 21 Ideas for the 21st Century[J]. Business Week,1999,8(11):78-167.

[2]Borko H,Bernier C. Emerging Technologies that Will Change the World[J]. Technology Review,2003,106(1):2249.

[3]AI-Karaki J N,Kamal A E. Routing Techniques in Wireless Sensor Networks:A Survey[J]. Wireless Communications,IEEE,Dee 2004,11(6):6-28.

[4]Motomura S,Isokawa T,Kawa H,et al. On Improvement of Anchor-Free Localization in ZigBee Sensor Network[C]//Proceedings of the 2012 Third International Conference on Networking and Computing. IEEE Computer Society,2012:362-366.

[5]Chen Yuanfang,Li Mingchun,Sun Weifeng,et al. GPS-Free and Anchor-Free Indoor Localization for Wireless Sensor Networks[J]. International Journal of Advancements in Computing Technology,2012,4(16):64-73.

[6]傅贤锋,黄亮,黄洁,等. 基于超声波四元阵测距的无锚节点定位算法研究[J]. 仪器仪表学报,2013,34(12):2874-2888.

[7]Emokpae L,Younis M. Surface-Reflection-Based Communication and Localization in Underwater Sensor Networks[J]. ACM Transactions on Sensor Networks(TOSN),2014,10(3):50.

[8]Shang Yi,Ruml Wheeler,Zhang Ying. Localization from Mere Connectivity[C]//Proceedings of the 4th ACM International Symposium on Mobile Ad Hoc Networking and Computing. 2003:201-212.

[9]刘健苗,许新忠,黄书广,等. 改进的分布式无线传感器网络多维标度定位算法[J]. 传感技术学报,2014,27(5):692-697.

[10]Capkun S,Hamdi M,Hubaux J P,et al. 2001. GPS-Free Positioning in Mobile Ad-Hoc Networks[C]//Proceedings of Hawaii International Conference on System Sciences. Maui,HW.

[11]Iyengar R,Sikdar B. Scalable and Distributed GPS Free Positioning for Sensor Networks[C]//Proc of IEEE Int’l Conf on Communications 2003. V01.1. Anchorage:IEEE Communications Society,2003,338-342.

[12]Xiaoli Li,Hongchi Slli,Yi Shang. A Map-Growing Localization Algorithm for Ad-Hoc Wireless Sensor Networks[C]//Proceedings of the Tenth International Conference on Parallel and Distributed Systems. 2004:39.

[13]Gerla M,Tsai J T C. Multicluster,Mobile,Ultimedia Radio Network[J]. Wireless Networks,1995,1(3):255-265.

[14]李德识,钟婧. 基于节点密度的传感器网络路由算法研究与设计[J]. 武汉大学学报:工学版,2005,38(4):75-78.

[15]程秀芝,朱达荣,张申,等. 基于RSSI差分校正的最小二乘-拟牛顿定位算法[J]. 传感技术学报,2014,27(1):123-127.

[16]Neal P,Joshua A N. Locating the Nodes:Cooperative Localization in Wireless Sensor Networks[J]. IEEE Signal Processing Magazine,2005,22(4):54-69.

王 明(1968-),男,副教授,全国高校计算机教学研究会理事,浙江省计算机教学研究会常务理事,宁波大红鹰学院物联网研究所常务副所长。近年来,承担或参与多项省部级、市厅级课题,主持宁波市自然科学基金项目。主要研究方向为无线传感器网络、信息系统分析与设计,发表学术论文20余篇,其中11篇论文由SCI/EI/ISTP收录,mr-wm@163.com;

陈庆章(1955-),男,教授,博士生导师,浙江工业大学计算机学院党委书记,主要研究方向是无线传感器网络、分布式处理与协同工作等。主持有国家自然科学基金、浙江省重大科技攻关课题和浙江省自然科学基金等多个项目,发表学术论文50余篇,其中37篇论文由SCI/EI/ISTP收录。

A Cooperative Node Localization Algorithm in Wireless Sensor Networks*

WangMing1,MengYun1,LiJing2,YingKeZhen3,4,ChenQingzhang3*

(1.Ningbo Dahongying University,Ningbo Zhejiang 315175,China;2.H3C Technologies Co.,Limited,Hangzhou 310053,China;3.Zhejiang University of Technology,Hangzhou 310023,China;4.Dongfang College,Zhejiang University of Finance and Economics,Haining Zhejiang 314408,China)

An anchor-free localization algorithm in wireless sensor networks is presented. Using nodes clustering and direction cooperation,the algorithm adjusts nodes’directions and coordinates with angle and range measurement to compute all nodes’ relative coordinates. Simulation results show that the network coverage,localization error rate and communication expense of the algorithm are better than clustering-based self-positioning algorithm.

wireless sensor networks;cooperative localization algorithm;anchor-free localization;nodes clustering

项目来源:宁波市自然科学基金项目(2013A610125);国家自然科学基金项目(61379023)

2014-11-25 修改日期:2015-02-05

C:6150P

10.3969/j.issn.1004-1699.2015.05.017

TP393

A

1004-1699(2015)05-0709-08