压电陶瓷换能器收发系统幅频特性建模与分析验证*

胡志钢,尹 钦,许姝菡

(1.宁波大学海运学院,浙江 宁波 315211;2.中国计量学院材料科学与工程学院,杭州 310018)



压电陶瓷换能器收发系统幅频特性建模与分析验证*

胡志钢1*,尹 钦1,许姝菡2

(1.宁波大学海运学院,浙江 宁波 315211;2.中国计量学院材料科学与工程学院,杭州 310018)

压电陶瓷超声波系统是实现物体探测的重要方法。本文基于压电陶瓷换能器收发系统的等效电路模型,通过引入声波衰减系数建立了发射换能器激励电压与接收换能器输出电压间的关系,并求解出了该等效电路模型的传递函数。实测数据与传递函数仿真数据对比表明,收发系统幅频特性的仿真曲线与实测曲线基本一致,验证了所给等效电路模型与传递函数的正确性。

压电陶瓷换能器;幅频特性;收发系统模型;等效电路

根据压电陶瓷材料的晶体结构、介电性质、弹性性质等物理特性,利用机-电类比、等效网络法等手段[1]构建的等效电路模型在现代压电陶瓷应用研究中得到广泛应用,是研究压电陶瓷特性常用分析方法,通过建立等效电路模型,可以揭示换能器工作原理并指导提高换能器的工作效率[2],早期典型代表有:Sherrit模型[3],Van Dyke模型、Guan模型[4]与复参数模型[5]等,主要研究等效电路对压电陶瓷换能器器件的各项物理性能的描述,使之更符合实际情况。

近年来则主要用于特式换能器的研发中,如:压电陶瓷薄圆片的机电等效模型[2]、切向去耦环形压电陶瓷堆等效电路模型[6]、Cymbal阵元等效电路模型[2,7]、长圆管换能器的机电等效电路[8]、厚度模式下压电等效电路[9]、压电换能器振动阻尼及分流压电换能器控制[10]等。

压电陶瓷换能器的另一研究方向是探伤、测距测速、识别等领域。该领域的换能器应用方式主要有二种:1收发一体,即发射和接收的工作由一只换能器完成;2收发分体,即接收与发射由两只以上的换能器共同完成。这两种应用方式都需要对收发系统进行性能分析、评价。上述等效电路模型应用均未涉及换能器组成收发系统。

参考前人研究[2-10]的基础上,本文基于动态信号分析,根据压电陶瓷换能器的频率特性仿真拟合参数,建立一种压电陶瓷收发系统等效电路模型。籍此实现收发系统的计算机仿真,使系统的规划设计可以先经过仿真测试调整,再由真实系统中实现,简化系统的设计工作和收发换能器匹配流程,提高工作效率。该等效电路模型见图1,图中虚线框内为换能器等效电路,其中接收换能器设置一个内阻为零的理想受激信号电压源Us来模拟压电效应所产生的电压[10-13]。

图1 收发分体换能器系统等效电路

1 发射和接收换能器系统等效电路及分析

通过对收集到的6个种类33只不同时期不同型号不同国家生产的换能器进行频率特性测试,其结果显示绝大多数压电陶瓷换能器的高次谐波中,仅有有限的3次谐波波峰较高,对收发系统性能指标影响较大,其余各次谐波因峰值较小,可忽略。因此为简化计算,收发系统等效电路的信号分析与传递函数求解仅按3次谐波分量来进行[10-13]。由于发射换能器和接收换能器的基波与高次谐波的传递函数计算较复杂,为简化计算过程采用了一些中间变量。

1.1 发射部分等效电路传递函数

发射换能器等效电路的传递函数:

(1)

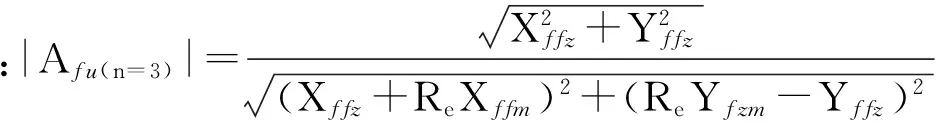
1.2 接收部分等效电路传递函数

接收换能器等效电路的传递函数:

(2)

式中:Z0为接收换能器Cs0和负载RL并联阻抗,Zss为Css的阻抗,Zsn为接收换能器除Rs0外的等效阻抗,

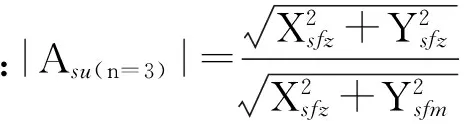
1.3 收发系统

发射换能器的Uf与接收换能器Us的物理作用过程如下:电发射端(Uf)—机发射端—声传导—机接收端—电接收端(Us)。在这个过程中,影响Uf和Us相互作用的因素非常复杂,如受发射换能器的发射功率、配对收发换能器的频率特性、超声波传播介质的衰减特性、被测物体对超声波的反射吸收性质以及换能器的应用方式等诸多因素,都可以影响Uf与Us的物理作用结果,为简化问题的复杂性,将上述因素统一由综合声波衰减系数αrlm来反映,使得Us=αrlmUf成立。

1.3.1 关于综合声波衰减系数αrlm

发射换能器用第1类(d型)压电方程中的第2个方程[1,11-12]描述:

(3)

接收传感器则用第3类(g型)压电方程中的第2个方程[1,11-12]描述:。

g型方程

(4)

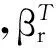
联立d型、g型第2个方程可得到用于描述压电陶瓷换能器收发系统的压电方程:

(5)

式中:式(5)上式为发射方程,下式为接收方程。因发射换能器样品的应力Tl=0,接收换能器的电位移Dr=0,收发系统压电方程可简化为:

(6)

式中:El=Uf/tcl,tcl为发射换能器压电陶瓷片厚度;Er=Us/tcr,tcr为接收换能器压电陶瓷片厚度。

综合声波衰减系数αrlm涵盖的物理过程:由于Uf的变化致使作为发射换能器的压电陶瓷产生应变Sl—逆压电效应(电发射端→机发射端),使介质产生机械振动—声波(机发射端→声传导),经过介质传递后抵达接收传感器生产应力Tr—机械振动(声传导→机接收端),通过压电效应转化为电场Er,产生受激信号源的电压信号Us(机接收端→电接收端),再通过接收换能器与负载的选频产生输出电压U0。根据式(6),接收换能器Us与的发射换能器的Uf关系为:

(7)

1.3.2 收发系统传递函数

根据式(1)、(2)、(7)可得:

则收发系统传递函数为:

模:

(8)

2 收发系统的实测与等效电路仿真验证

实验换能器选型号为:EU1640BCH(直径16mm)的防水型压电陶瓷换能器作为测试样品进行实验。该换能器标称频率为:40kHz;发射声压at10V(0dB=0.02mPa):≥110dB,接收灵敏度at40kHz(0dB=V/μbar):≥-75dB,静电容量at1kHz,<1V):1 800±30%pF,生产年份:2013年,数量:24只。实验结果与对应的换能器等效电路仿真结果进行比较验证。下文将4个样品组成的3对收发系统的实验测试与仿真验证结果进行全面的对比与验证。

2.1 样品的频率特性实测与等效电路仿真验证

样品的静电容量C0使用UT58E数字万用表(基本精度±(3%+40))测量,其值为10次测量平均值,测试环境温度8 ℃,测试样品与相应静电容值C0见表1。

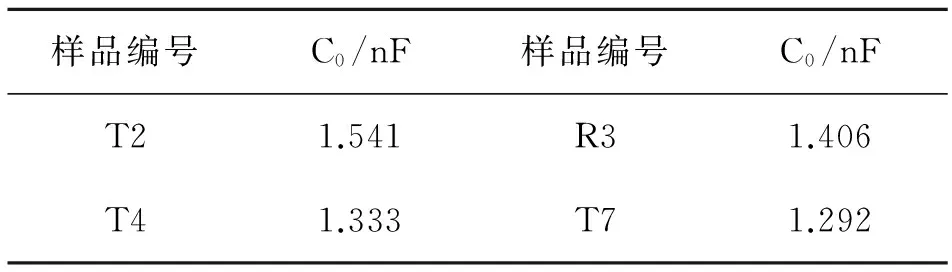
表1 样品静态电容

根据频率特性测试等效电路,见图2,虚线框内为被测换能器的等效电路,ZE为信号发生器内部阻抗,r(10kΩ)为测量电阻。实验仪器:信号发生器WY1640、安捷伦34972A+34901A多路采集卡和泰克TDS1002示波器,实测与仿真结果见图3,样品的3次谐波频率特性实测与仿真拟合参数见表2,从图3可以看出,根据表2参数进行仿真所得结果与实测数据基本吻合,因此我们认为表2中的参数可作为样品换能器收发系统的仿真参数使用。

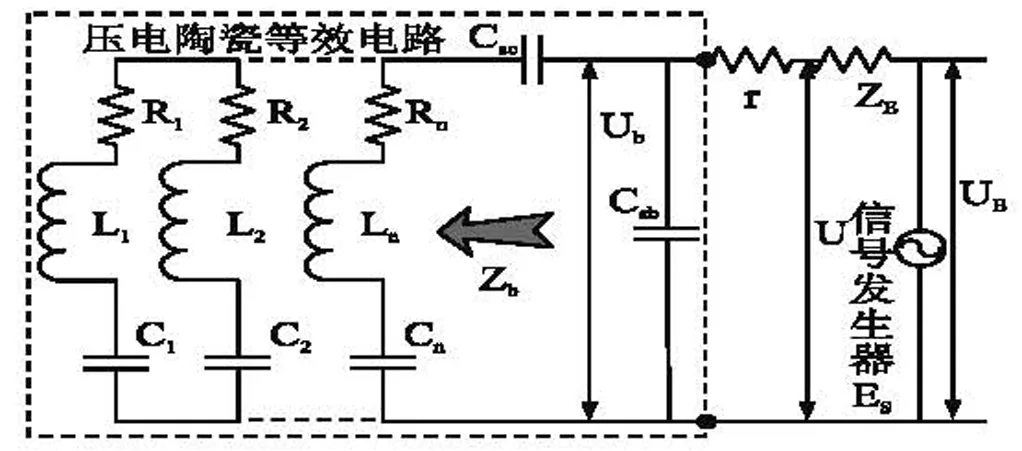
图2 频率特性测试电路

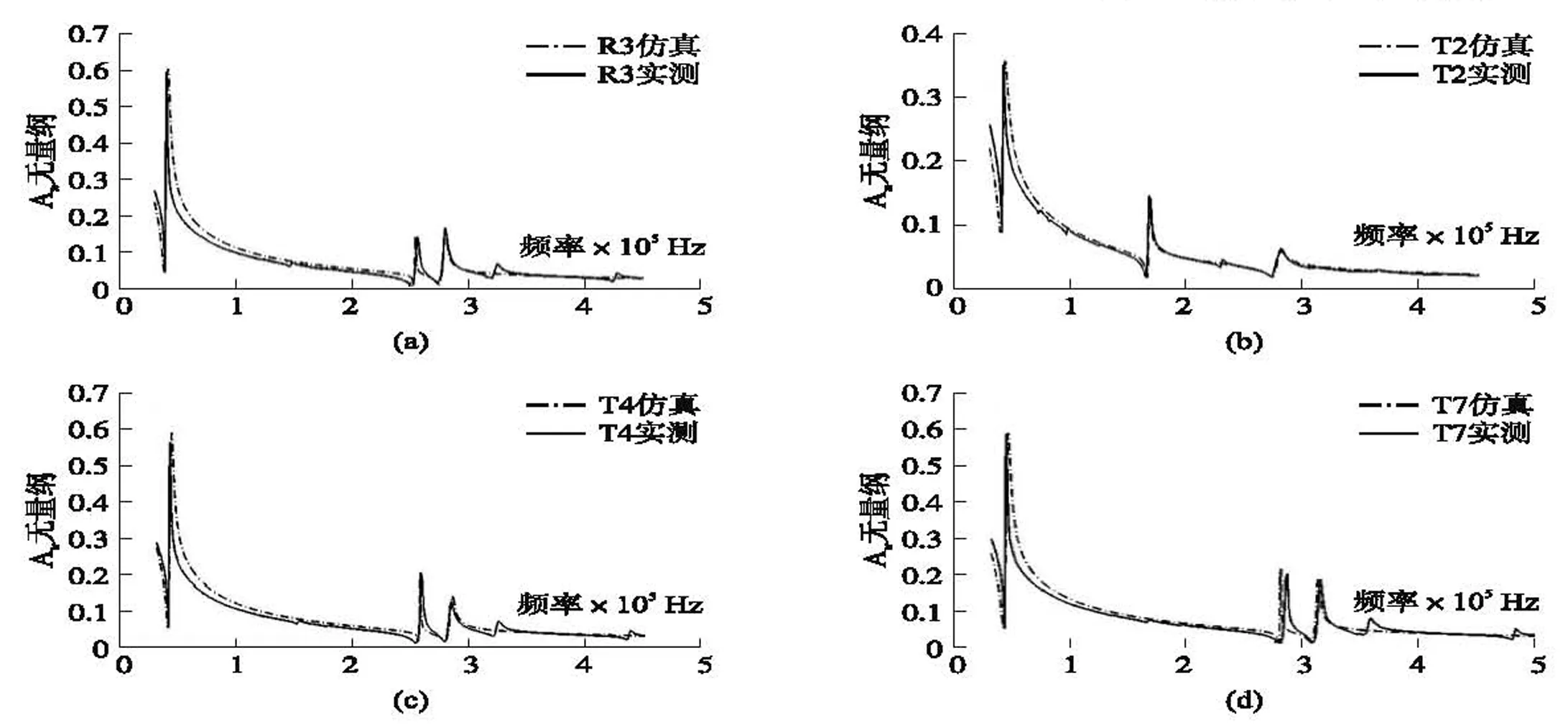
图3 样品换能器频率特性实测与仿真结果

续表2

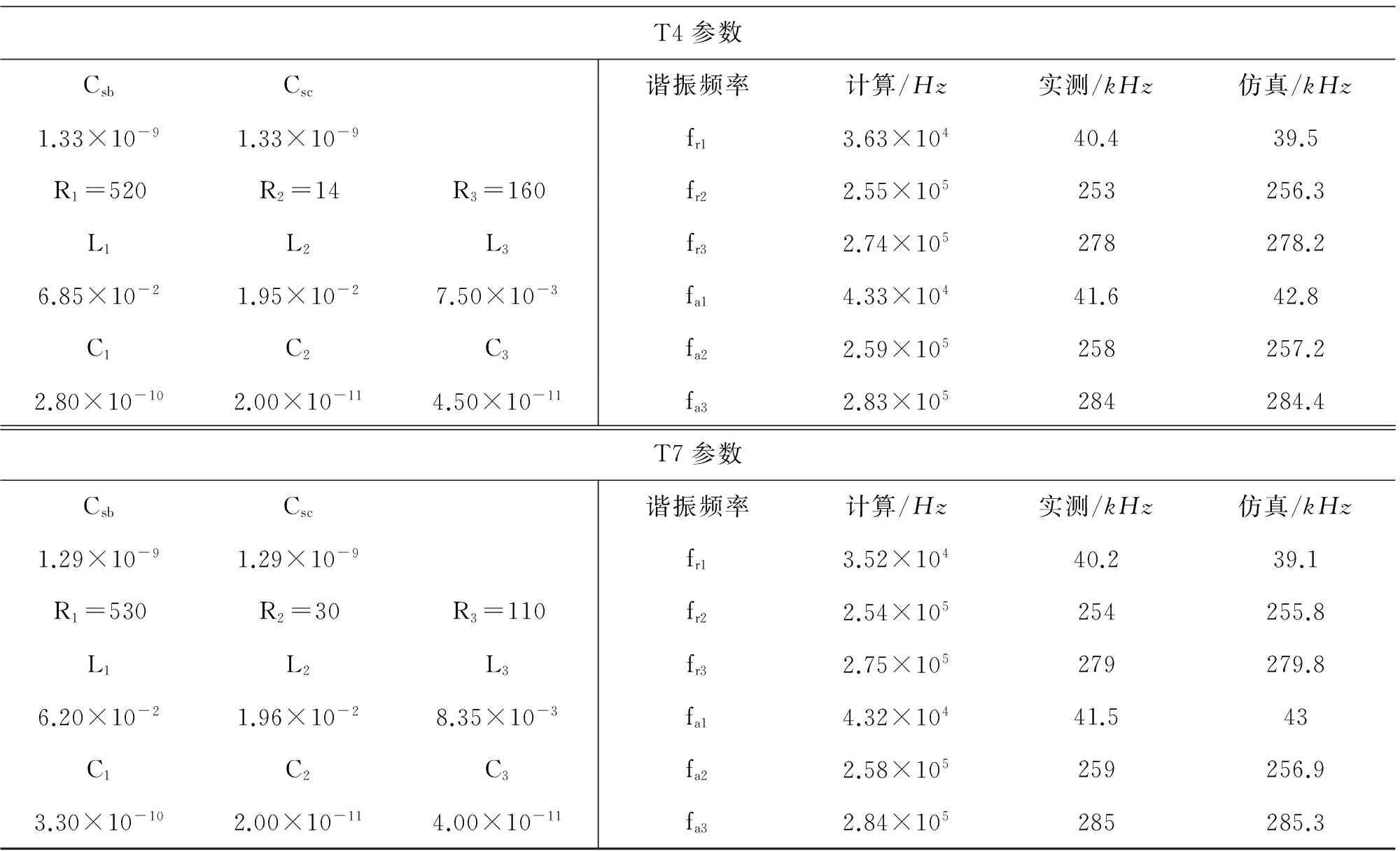
T4参数CsbCsc谐振频率计算/Hz实测/kHz仿真/kHz1.33×10-91.33×10-9fr13.63×10440.439.5R1=520R2=14R3=160fr22.55×105253256.3L1L2L3fr32.74×105278278.26.85×10-21.95×10-27.50×10-3fa14.33×10441.642.8C1C2C3fa22.59×105258257.22.80×10-102.00×10-114.50×10-11fa32.83×105284284.4T7参数CsbCsc谐振频率计算/Hz实测/kHz仿真/kHz1.29×10-91.29×10-9fr13.52×10440.239.1R1=530R2=30R3=110fr22.54×105254255.8L1L2L3fr32.75×105279279.86.20×10-21.96×10-28.35×10-3fa14.32×10441.543C1C2C3fa22.58×105259256.93.30×10-102.00×10-114.00×10-11fa32.84×105285285.3

表2中未注明的物理量量纲:电感H,电容F,电阻Ω,Csc忽略了部分受夹,取Csc=Csb=C0;fr1～fr3为谐振频率,fa1～fa3为反谐振频率。谐振频率计算公式[11,13]:

2.2 发射与接收等效电路的实测与仿真验证

实验测试电声系统[15]见图4。为使换能器实测数据有统一的对比环境,将收发系统放置在相同的环境中进行测试,下面进行的实测与仿真均以空气作为介质(可视为无限空间),发射与接收换能器间距设置在L=30cm进行。

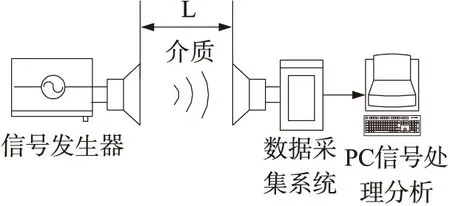
图4 测试环境

根据2.1的结论,以表2参数进行收发等效电路的仿真与样品实测比较,结果见图5。图中发射换能器数据做了归一化处理,并为了便于与接收换能器数据的比较,将发射换能器数据按比例缩小至接收换能器测试数据同一数量级。图5中T7为发射换能器,分别与R3、T2、T4接收换能器组成收发系统。

从图5(a)～(c)可以看出,发射换能器的实测数据与等效电路模型的仿真结果吻合度较高,接收换能器的实测数据与等效电路模型的仿真结果基本吻合,二者的基本幅频一致,但在数值上存在一定的偏差。图6是图5(a)的局部放大,从图6可以看出,无论实测数据还是理论仿真结果都反映了发射换能器对接收信号幅频特性的影响,实测与仿真结果基本一致。图5(d)是收发一体的发射实测与收发系统仿真效果,从中可看出,压电陶瓷换能器发射频率的幅度在fr附近达到极值,而接收频率的幅度在fa附近达到极值,实测与仿真结果相符。

2.3 收发等效电路在换能器配对中的实测与仿真验证

重复2.1、2.2节中的实验,测试了60对换能器组成的收发系统数据。对实测数据进行收发效果统计,并将统计结果与相应的收发系统等效电路仿真结果分别进行基波、2次谐波和3次谐波的收发效果进行对比,对比的结果表明:基波的实测与仿真符合率为73.3%;2次谐波符合率为86.7%;3次谐波符合率为76.7%,综合符合率达到78.9%。

图5 样品发射与接收实测与仿真结果

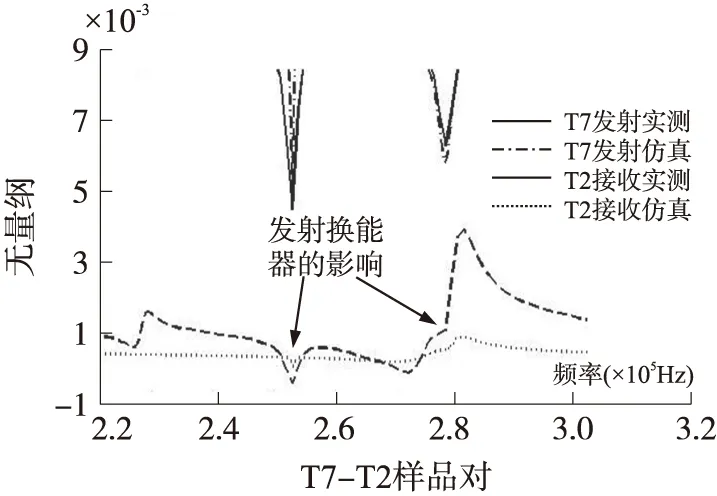
图6 发射换能器对系统频谱特性的影响

3 结论

根据压电陶瓷收/发换能器的频率特性拟合得到相应换能器的仿真拟合参数,以此参数为基础,通过本文提出的换能器收发系统等效电路模型得出仿真结果,与实际测量的收发系统结果进行对比:

①实验证明,在空气作为介质的条件下,不同的收发换能器间距L仅影响接收换能器的信号幅度,不影响实测曲线的变化趋势,模型的仿真与实测曲线基本一致。

②发射换能器端电压Uf与接收换能器响应电压U0的关系综合反映了超声波传输介质环境的衰减特性、发射换能器的逆压电效应与接收换能器的压电效应的综合情况,因而在超声波声波介质环境综合衰减函数αrlm特定的条件下,可实现对收发系统性能的计算机仿真分析,提高系统性能评价的工作效率,简化收发换能器匹配流程。

③在超声波收发系统确定的情况下,可对不同超声波传播介质的衰减函数αrlm进行计算机仿真测试,使系统设计可以先经过仿真测试、修正,再在真实系统中实施,提高系统设计验证效率。

[1] 王春雷,李吉超,赵明磊. 压电铁电物理[M]. 科学出版社,2009:91-95,139-148.

[2]彭海军,贾绍文,杨建新,等. 钹式换能器等效电路模型研究[J]. 传感技术学报,2014,27(6):747-751.

[3]Sherrit S,Wiederick H D,Mukherjee B K,et al. An Accurate Equivalent Circuit for the Unloaded Piezoelectric Vibrator in the Thickness Mode[J]. Journal of Physics D:Applied Physics,1997,30(16):2354-2363.

[4]Jina Kim,Benjamin L Grisso,Jeong K Kim,et al. Electrical Modeling of Piezoelectric Ceramics for Analysis and Evaluation of Sensory Systems[J]. SAS 2008—IEEE Sensors Applications Symposium,Atlanta,GA,2008:12-14.

[5]叶会英,禹延光. 压电振子复参数等效电路模型研究[J]. 电子元件与材料,2004,23(3):10-17.

[6]刘世清,许龙,张志良,等. 夹心式径向复合压电起声换能器[J]. 声学学报,2014,39(1):104-110.

[7]高全芹. Cymbal型压电换能器电压-位移特性建模与分析[J]. 传感技术学报,2012,25(4):492-495.

[8]林书玉,王帅军,付志强,等. 径向极化压电陶瓷长圆管复合超声换能器的径向振动[J]. 声学学报,2013,38(3):354-363.

[9]陈雨,文玉梅,李平,等. 压电换能器耗散因子的等效电路参数表示[J]. 传感技术学报,2006,19(4):1074-1078.

[10]Reza Moheimani S O,Senior Member,IEEE. A Survey of Recent Innovations in Vibration Damping and Control Using Shunted Piezoelectric Transducers[R]. IEEE Transactions on Control Systems Technology,2003,11(4):482-494.

[11]ANSI/IEEE Std 176—1987,IEEE Standard on Piezoelectricity[S]. 1987.

[12]惠德畅,魏汉,张万飞,等. 结构压电机电阻抗谱测试方法[J]. 信息化研究,2013,39(5):26-29.

[13]GB/T 3389—2008 压电陶瓷材料性能测试方法[S]. 性能参数的测试.

[14]王家胜,董文中,曾晟,等. 超声波在煤粉中的衰减特性的仿真[J]. 锅炉技术,2005,36(1):49-52.

[15]刘丽,陈雨,徐志龙,等. 基于ANSYS的埋入混凝土中压电陶瓷谐振频率分析[J]. 传感技术学报,2014,27(1):85-89.

Analysis of an Equivalent Circuit Model for the Transducer Transceiver System of Piezoelectric Ceramic Transducer*

HUZhigang1*,YINQing1,XUShuhan2

(1.Maritime College of Ningbo University,Ningbo Zhejiang 315211,China;2.School of Materials Science and Engineering,China Jiliang University,Hangzhou 310018,China)

Piezoelectric ceramic ultrasonic system(PCUS)is an important method for object detection. According to the equivalent circuit model of PCUS,the attenuation coefficient from transmitting excitation voltage to receiving signal voltage is analyzed in detail. And,transfer function of the given equivalent circuit model for PCUS is presented in this paper. The experiment shows that amplitude-frequency curve of the simulated data and measured data for transceiver system are almost the same. That proved the correction of the given equivalent circuit model and transfer function of PCUS.

piezoelectric ceramic transducer;amplitude-frequency characteristics;transceiver system model;equivalent circuit

胡志钢(1961-),男,高级实验师。主要研究方向为轮机自动化、机器故障检测、压电传感器应用,huzhigang@nbu.edu.cn;

尹 钦(1993-),男,江西萍乡人,本科生。主要研究方向为机器人技术、传感器及多信息融合,751824337@qq.com;

许姝菡(1994-),女,浙江省宁波人,本科生。主要研究方向为金属表面处理、压电陶瓷材料成型与制备,574970972@qq.com。

项目来源:宁波大学学科项目(xkl141048)

2014-09-29 修改日期:2015-02-05

C:2860A;7230

10.3969/j.issn.1004-1699.2015.05.006

TP212.1

A

1004-1699(2015)05-0641-07