微型之字形压电式能量收集器输出电压的建模和仿真*

李如春,征 琦,施朝霞

(浙江工业大学信息工程学院,杭州 310014)



微型之字形压电式能量收集器输出电压的建模和仿真*

李如春*,征 琦,施朝霞

(浙江工业大学信息工程学院,杭州 310014)

为了有效解决无线传感器网络节点的供电难题,提出之字形结构的微型压电式能量收集器。相比于传统的直悬臂梁,此结构等效加大了压电梁的长度,降低了系统的固有振动频率。建立了之字形压电梁的本构方程和受迫振动方程,推导得到其输出电压的频域表达式。基于之字形压电梁的结构,利用ANSYS软件对其进行了谐响应分析。仿真结果表明,压电梁的输出电压在各阶固有振动频率处存在极值,符合理论分析的结果;输出电压大小随压电梁长度增加而降低,随压电梁宽度增加而升高,但均为非线性关系;压电梁末端质量块的长度和厚度、基体层厚度减小时,会导致输出电压的增大。在论文中所提出的结构尺寸下,10根直梁构成的之字形结构压电梁,在其一阶固有振动频率处,输出电压可达10 V以上,符合无线传感器网络节点的实际供电需求,证明了之字形压电梁结构的有效性。

微型能量收集器;之字形压电梁;输出电压;解析建模;仿真分析

无线传感器网络被人们视为是在多种应用环境中连续收集数据的一种重要方法,当传感器节点分布广泛、数量巨大、特别是地处偏僻处时,其难点之一是如何为传感器节点供电。许多应用要求传感器节点小于1角硬币,通常利用钮扣型电池供电,但电池有限的能量限制了无线传感器网络的稳定性、使用寿命和应用范围。目前,解决该问题的方法包括了节能算法和协议,以及环境能量采集。无线传感器网络各层次的节能协议只能在一定程度上延长传感器网络的寿命,无法从根本上解决能量有限的问题,而能量收集器则可以把周围环境中的能量转化为电能,有效解决传感器节点的供电问题。

自然界环境中存在的能量多种多样,其中振动能量的存在最为广泛,受环境的约束也最小。振动驱动的能量收集器根据能量转换原理的不同,可分为电磁式[1]、静电式[2]、磁致伸缩式[3]、压电式[4]等,其中压电式能量收集装置因为体积小,能量密度高,不需要外加电压源等优点而得到广泛的应用[5]。压电式能量收集器的工作原理是利用环境的振动来激励压电悬臂梁能量收集器产生受迫振动,从而引起压电层在激振力作用下发生机械应变,经材料内部的机电耦合效应将机械应变能转变为电能[6]。常规的微型压电式能量收集器一般采用直梁结构,由于尺寸较小,固有振动频率可达几千赫兹,而自然环境中存在的振动源频率一般低于200 Hz,两者无法形成共振,导致其输出电压较小,输出功率一般只有微瓦量级,不能满足无线传感器网络节点正常工作时毫瓦量级的功率需求。

第一个MEMS微型能量收集器由Lu[7]等人在2004年设计,采用直梁结构,梁的宽长比为1/10,其固有振动频率达到3 kHz;随后,Fang等人[8]尝试了更低的梁宽长比(1/100),使其固有振动频率降低到600 Hz;但压电梁长度的增加受微型器件空间尺寸的限制,压电层宽度的减小受MEMS制作工艺最小线宽的限制,因此,无法通过梁宽长比的持续减小来降低梁的固有振动频率。由此,开始了振动式能量收集器结构上的改进研究,螺旋型结构梁[9]被提出,但此结构以扭转振动为主,需要外界对压电材料施加剪切力,而在实际环境中很难获得此力,推广应用受到限制。2011年,Huicong Liu等[10]提出了利用PZT薄膜阵列构成的压电式悬臂梁结构,当该结构由并联电路连接时,固有频率达38.5 Hz,但最大输出功率只有11.6 nW。2014年,重庆大学佘引等[11]提出共质量块悬臂梁阵列结构,开路输出电压有效值达到9.16V,外接负载200 Ω时,输出功率为151.8 μW。基于上述研究基础和现状,论文提出之字形结构压电梁的微型能量收集器,并对此结构建立解析模型和进行仿真分析。

1 之字形结构微型压电式能量收集器输出电压的解析建模

压电式能量收集器一般采用d31模式的悬臂梁式结构[12],其固有振动频率ωn为

(1)

式中:m是悬臂梁的质量,k是刚度系数,与臂长成反比[13]。

由式(1)可知,要降低悬臂梁的固有振动频率,可通过等效加大梁的长度,论文提出的之字形结构悬臂梁就基于此原理,其Y轴方向的俯视图如图1所示。图1中,悬臂梁由多根处于同一平面的直悬臂梁组合而成,每根直臂梁与相邻梁之间通过很短的连接件相连。悬臂梁是一种复合型压电梁,其截面呈矩形。制作时,可选取Si基片作为衬底,采用热氧化法在基片上生长一定厚度的SiO2层,在二氧化硅表面磁控溅射Pt/Ti复合层作为压电层的下电极,通过溶胶—凝胶法(sol-gel)在Pt/Ti电极上旋涂LaNiO3以及PZT(锆钛酸铅,化学式为PbZrxTi2-XO3,PZT)压电层,并进行相应的热处理,然后光刻和湿法腐蚀LaNiO3以及PZT压电层,在PZT上磁控溅射一层Al薄膜,光刻图形化得到上电极;通过光刻腐蚀形成之字形结构悬臂梁,悬臂梁末端的质量块由金属Ni淀积构成,之后释放结构。为制作方便,连接件选用与直臂梁完全相同的材质。

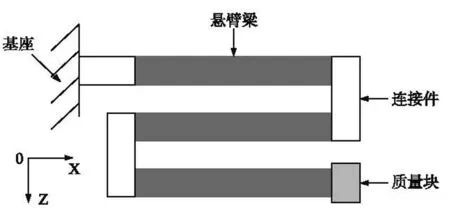
图1 之字形结构压电梁Y轴方向的俯视示意图

论文采用的压电材料是d31模式,此振动模式的应力与产生的电场方向互相垂直。弯曲振动时材料受到的是正拉、压应力,和能量收集器的电极表面垂直,将在电极表面因压电效应而产生电荷;而扭转振动时材料受到的是剪切力,剪切变形在电极平面上产生的电荷极少[15]。因此,扭转振动相对于弯曲振动,对压电梁的有效变形贡献小很多。在下面的之字形结构压电梁输出电压的解析建模中,忽略扭转振动的影响。

沿厚度方向(Y轴方向)极化的压电梁的弯曲振动,其本构方程为

(2)

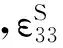
对于由n根直梁构成的之字形压电梁,根据梁固定端、自由端的边界条件以及哈密顿原理,并结合上述本构方程,可推出第i根压电复合梁的受迫弯曲振动方程[14]如下:

(3)

式中:v(t)表示压电梁的输出电压,yb表示基座沿梁横截面方向的位移,yrel是之字形梁相对基座的位移,E为梁结构的弹性模量,I为梁对于水平x轴方向的惯性矩,EI为压电梁的等价截面弯曲刚度,ρ为梁密度,A为梁横截面的面积,l是单根梁的长度,mtip是梁自由端质量块的质量。δ(x)是单位脉冲函数,λ是与梁的尺寸和材料特性相关的耦合因子[15]。

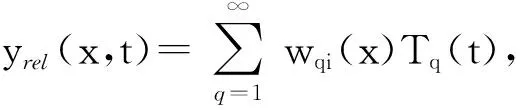
(4)

式中:Pi为转换开关的值,可取1或-1,由实际电流的方向决定。

将式(4)两边分别乘以wqi并沿0至l积分,由于模态形状的正交性有

(5)

(6)

将式(6)进行傅里叶变换,可得

(7)

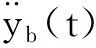
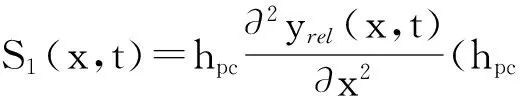
(8)

压电层产生并由电极收集的电荷q(t),可以通过将电位移沿着电极面积分得到,假设压电层宽度是b,则第i根梁的PZT层产生的电流为

(9)

将上式(9)写成模态形式

(10)

为求总电流,考虑之字形结构中所有直梁的电流总和及各梁之间的转换开关值Pi,并将其作傅里叶变换,得到之字形梁结构输出的总电流

(11)

负载上的电压为负载阻抗与电流的乘积,即V(ω)=Z(ω)Itotal(ω),结合式(11),并将前述已知的kq、γq等参量代入,整理可得

(12)

由式(7)和式(12)可推出V(ω)的表达式如下

(13)

由于作为电源的能量收集器和负载电阻并联,因此电路总阻抗的导纳为

(14)

式中:RL是负载电阻,cb表示能量收集器的电容。

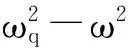
(15)

由式(15)可知,当ω=ωq时,输出电压可达到一极值;输出电压与之字形梁的结构参数有关,相互之间是一种较复杂的非线性关系。

2 之字形压电梁输出电压的仿真分析

为直观表述压电梁输出电压与各影响因素之间的关系,下面对其进行仿真分析。

根据图1所示的之字形压电梁结构,取尺寸大小如表1所示。质量块的参数为:密度ρm=8 800 kg/m3,泊松比为μm=0.31,弹性模量为Em=2.01×1011N/m2;硅基材料参数:弹性模量Es=1.9×1011N/m2,密度ρs=2 330 kg/m3,泊松比μs=0.23;PZT-5H参数:密度ρp=7 750 kg/m3、泊松比μp=0.27,弹性常数矩阵[c]、压电常数矩阵[e]、介电常数矩阵[ε]分别如下[16].

利用大型有限元仿真软件ANSYS,根据上述材料与几何参数建立之字形压电梁的有限元仿真模型。建模时,由于绝缘层、电极层与压电层和衬底层相比很薄,结构中可以忽略。在下述仿真中,取组成之字形梁的直悬臂梁个数n=10,外接150 kΩ电阻,之字形梁的自由端施加许用应力范围内的正弦激励F=0.03sin(ωt)N。

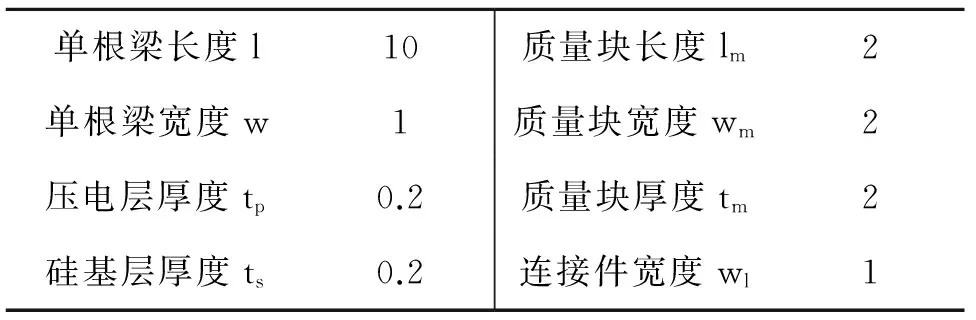
表1 之字形梁的结构尺寸(单位:mm)

图2是之字形梁稳态响应输出电压的仿真结果。由图2可知,当激励源的振动频率变化时,之字形梁的稳态输出电压分别在其各阶固有振动频率处达到极值,这与前述理论分析结果一致。输出电压在一阶固有频率处最大,可达14 V左右,其他各阶处的输出电压幅值要小很多。由于一阶固有振动频率在200 Hz以下,能与自然界存在的低频振动源形成共振,自然界存在的其他较高振动频率的激励源,虽也能与压电梁的高阶振动模态形成共振,但振动能量转换的输出电压相对一阶振动也要小很多。

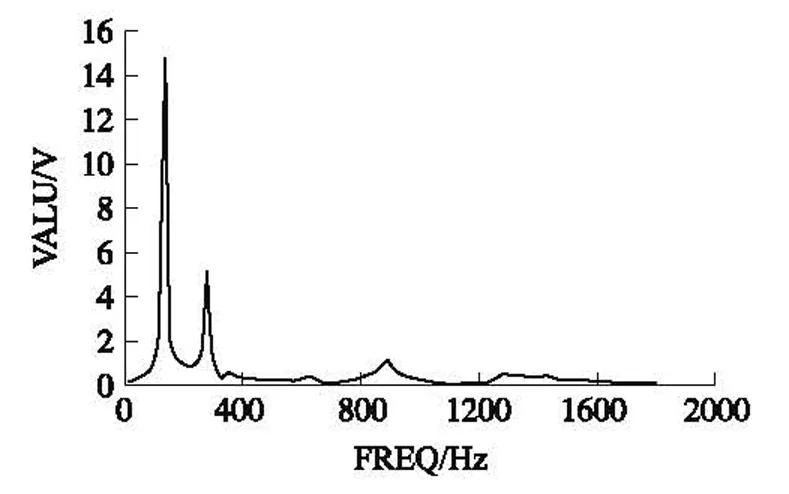
图2 之字形梁输出电压与激励频率的关系

图3 组成之字形结构的直悬臂梁数目n与其输出电压的关系

随着组成之字形压电梁的直悬臂梁数目n的增加,在相同大小的正弦激励下,其产生的电压也越大,仿真结果如图3所示。这是因为随着梁数目的增多,其稳态响应产生的位移增大,相应的应变能变大,压电层表面产生的自由电荷也越多。因此,直梁根数的增加有助于电能的获取,但其增加是有限制的,否则容易断裂。

之字形结构压电梁的谐响应输出电压与梁的结构尺寸直接相关,改变其大小,得到一阶振动时输出电压与结构参数的关系曲线如图4所示。由图4(a)、4(b)可知,输出电压随着压电梁长度的增加而降低,随宽度的增加而升高,当梁宽增加到1.2 mm时,电压增长趋缓,对输出电压的影响变弱。图4(c)显示,压电层基体的厚度越小,其输出电压峰值越大,且其大小的变化对输出电压的影响较大。当ts=0.5 mm时,其峰值电压为9 V,而当ts减小到0.1 mm时,峰值电压可达17 V。图4(d)、4(e)表明,质量块的厚度和长度以1 mm为单位减小时,其输出电压峰值在几伏范围内增加。相较于基体层厚度,质量块对电压的影响较小。

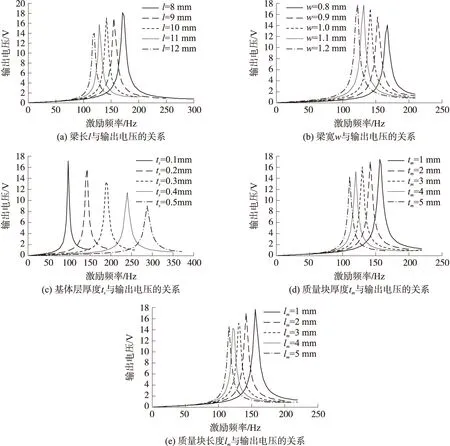
图4 之字形梁的结构参数与输出电压之间的关系曲线

3 结束语

论文提出之字形结构的微型压电式能量收集器,建立了压电复合梁的受迫振动方程和本构方程,通过求解和推导,得到系统输出电压的频域表达式。之字形压电梁输出电压解析模型的理论分析表明,当外加激励源的频率与压电梁的固有振动频率一致时,输出电压达到极值;输出电压的大小与之字形梁的结构参数有关,相互之间是一种较复杂的非线性关系。为直观表述输出电压与各影响因素之间的关系,论文对之字形压电梁进行了ANSYS仿真分析。仿真结果表明,输出电压随组成之字形压电梁的直梁数目增加而增大;随着压电梁长度的增加,输出电压降低;压电梁宽度增加,输出电压升高;质量块长度和厚度的减小,会导致输出电压的增大,但增幅有限;相比于质量块,基体层厚度对电压的影响较大,基体层厚度越小,其输出电压峰值越大;但这些结构尺寸的增加或减少不是无限制的,需考虑实际MEMS制作工艺的条件限制,同时需防止压电梁出现断裂。当组成之字形结构压电梁的直臂梁个数为10时,在所允许正弦激励F=0.03sin(ωt)N作用下,之字形压电梁的输出电压可达10 V～20 V,有望为间断性工作的无线传感器网络节点供电。

[1] 杜小振,王刚,卞丰. 电磁发电微电源结构设计与输出电能的动态仿真分析[J]. 传感技术学报,2013,26(8):1088-1091.

[2]Sehwan K,Kukjin C,Sungil B. Temperature Effect on the Vibration-Based Electrostatic Energy Harvester[C]//IEEE TENCON2011-2011 IEEE Region 10 Conference:1317-1320.

[3]Hao Feng,Pei Yongmao,Fang Daining. The Effects of Interface Misfit Strain and Surface Tension on Magnetoelectric Effects in Layered Magnetostrictive-Piezoelectric Composites[J]. Journal of Applied Physics,2013,114(4):044109-044109-8.

[4]Phipps A,Nishiba T. System Modeling of Piezoelectric Energy Harvesters[J]. IEEE Trans Power Electron,2012,27(2):790-802.

[5]Zhu Meiling,Emma Worthington,Ashutosh Tiwari. Design Study of Piezoelectric Energy-Harvesting Devices for Generation of Higher Electrical Power Using a Coupled Piezoelectric-Circuit Finite Element Method[J]. IEEE Transactions on Ultrasonics,Ferroelectrics,and Frequency Control,2010,57(2):427-437.

[6]Roundy S,Wright P K. A Piezoelectric Vibration Based Generator for Wireless Electronics[J]. Smart Materials and Structures,2004,12(4):4156-4162.

[7]Lu F,Lee H,Lim S. Modeling and Analysis of Micro Piezoelectric Power Generators for Micro-Electromechanical-Systems Applications[J]. Smart Materials and Structures,2004,13(1):57-63.

[8]Fang H,Liu J,Xu Z. Fabrication and Performance of MEMS-Based Piezoelectric Power Generator for Vibration Energy Harvesting[J]. Microelectron,2006,37(11):1280-1284.

[9]Choi W,Jeon Y,Jeong J. Energy Harvesting MEMS Device Based on Thin Film Piezoelectric Cantilevers[J]. Electroceramics,2006,17(2-4):543-548.

[10]Liu H,Quan C G,Tay C J,et al. A MEMS-Based Piezoelectric Cantilever Patterned with PZT Thin Film Array for Harvesting Energy from Low Frequency Vibrations[J]. Physics Procedia,2011(19):129-133.

[11]佘引,温志渝,赵兴强,等. MEMS压电阵列振动能量收集器[J]. 传感技术学报,2014,27(8):1033-1037.

[12]Marco F,Vittorio F,Michele G,et al. Piezoelectric Multifrequency Energy Converter for Power Harvesting in Autonomous Microsystems[J]. Sensors and Actuators,2008,A(142):329-335.

[13]Biship R E D,Johnson D C. The Mechanics of Vibration[M]. Oxford:The Syndics of The Cambridge University Press,1960.

[14]Erturk A,Inman D. A Distributed Parameter Electromechanical Model for Cantilevered Piezoelectric Energy Harvesters[J]. ASME J Vibr Acoust,2008,130:041002.

[15]Karami M A,Inman D J. Electromechanical Modeling of the Low-Frequency Zigzag Micro-Energy Harvester[J]. Intelligent Material Systems and Structures,2011,22:271-282.

[16]压电陶瓷的材料特性[EB/OL]. http://www.fujicera.co.jp/product/c/index.html,2013-08-08.

Modeling and Simulating for Output Voltage of Piezoelectric Energy Harvester*

LIRuchun*,ZHENGQi,SHIZhaoxia

(College of Information Engineering,Zhejiang University of Technology,Hangzhou 310014,China)

In order to effectively solve the power problem of wireless sensor network node,zigzag microstructure for piezoelectric energy harvester is proposed. Compared to the traditional straight cantilever,this structure is equivalent to increase the length of the piezoelectric beam,reduces the natural vibration frequency of the system. To establish the constitutive equations and forced vibration equations of zigzag piezoelectric cantilever,the output voltage expression is derived. Based on structure of zigzag cantilever,the harmonic response analysis is simulated by ANSYS software. Simulation results show that the output voltage is present extremes in the order natural vibration frequencies,it is in accord with the results of theoretical analysis;the output voltage amplitude increases when piezoelectric beam length decreases,with the increase of the piezoelectric beam width,the output voltage increases,that is non-linear relationship;when the length and thickness of quality block,the base layer thickness decrease,the output voltage will increase. Based on the structure size proposed in the paper,the zigzag cantilever composed of 10 straight beams,in the first-order natural vibration frequencies,the output voltage is up to 10 V,it meets the actual power requirements of wireless sensor network nodes,proves the validity of the zigzag piezoelectric cantilever structure.

micro energy harvester;zigzag piezoelectric cantilever;output voltage;analytical modeling;simulation analysis

李如春(1968-),女,浙江青田人,副教授,博士,主要研究方向为微型传感器设计、视频信号处理等,lrc@zjut.edu.cn;

征 琦(1988-),女,安徽宿州人,硕士研究生,主要研究方向为压电式能量收集器的设计与建模,zhengiq_325@outlook.com。

项目来源:国家自然科学基金项目(61306090)

2014-09-30 修改日期:2015-02-09

C:7230

10.3969/j.issn.1004-1699.2015.05.004

TM919

A

1004-1699(2015)05-0629-06