基于陀螺辅助的磁罗盘抗干扰测量方法
龙达峰,刘 俊,2*,李 杰,苏 文
(1.中北大学电子测试技术重点实验室,太原 030051;2.中北大学仪器科学与动态测试教育部重点实验室,太原 030051;3.中国人民解放军266011部队,北京 102600)
基于陀螺辅助的磁罗盘抗干扰测量方法
龙达峰1,刘 俊1,2*,李 杰1,苏 文3
(1.中北大学电子测试技术重点实验室,太原 030051;2.中北大学仪器科学与动态测试教育部重点实验室,太原 030051;3.中国人民解放军266011部队,北京 102600)
为了解决磁罗盘使用过程中受到的磁干扰和加速度干扰影响测量精度问题。提出了基于陀螺辅助的磁罗盘抗干扰测量方法。选取磁罗盘姿态四元数微分程和传感器误差模型共同构建系统的滤波模型,由自适应卡尔曼滤波算法实现磁罗盘姿态估计,并借助于无磁转台对测量方法进行了实验验证,结果表明该方法是可有效实现磁罗盘的抗干扰测量,且能提高磁罗盘测量精度。
电子磁罗盘;陀螺;抗干扰测量;自适应卡尔曼滤波器
磁罗盘是利用地球磁场信息解算航向、姿态的测量仪器,又称为磁航向系统[1-3]。传统的磁罗盘姿态传感器由加速度计和地磁传感器组成,利用加速度计测量所到重力加速度矢量信息,按矢量投影关系首先解算出磁罗盘的俯仰角和横滚角,然后根据地磁传感器测量所得地磁场信息计算出磁航向角[1-5]。要求磁罗盘处于绝对的静止或非加速度状态下进行测量,否则加速度计测量所得不仅仅是当地重力加速度,还会叠加上外加速度信息,其必然会带来严重的解算误差。而在实际测量过程中,磁罗盘不可避免存在线加速度或者外界磁场干扰不利因素的影响[4-9]。因此,传统磁罗盘测量解算精度很大程度取决于传感器精度和使用环境的好坏[7-11]。针对传感器精度问题,通常采用传感器的校准方法来提高其测量精度,包括事前标定与在线校准方法,或者借助于文献[5-8]所述最小二乘法、椭圆假设补偿法和椭球拟合等处理方法进行误差补偿。通过上述补偿措施可以在一定程度上提高传统磁罗盘测量精度,但还是无法根本上解决在实际使用过程中的线加速度干扰问题。究其原因是无法去除非重力加速度信息,这也是传统磁罗盘要求处于绝对的静止或非加速度运动测量的原因所在。针对上述问题,本文提出了基于陀螺仪辅助的磁罗盘抗干扰测量方法,以解决磁罗盘在实际使用过程中不可避免的外界磁场干扰和线加速度干扰等不利因素影响。该方法的独特性在于存在线加速度干扰时,磁罗盘利用陀螺仪输出信息进行惯导姿态递推解算,可以保证在大线加速度干扰时也能实现较为准确的测量。
1 基于陀螺辅助的磁罗盘滤波方案
本文所采用的基于陀螺辅助的磁罗盘测量方法是在传统的磁罗盘基础上增加陀螺仪进行辅助测量,磁罗盘姿态滤波方案如图1所示。

图1 陀螺辅助的磁罗盘姿态滤波方案
选取磁罗盘姿态四元数、加速度计以及地磁传感器的零偏为滤波器状态变量,并综合姿态四元数微分程和传感器误差模型共同构建磁罗盘测量系统的滤波模型;并以三轴加速度计和地磁传感器的测量输出作为滤波器的量测信息,由扩展卡尔曼滤波算法完成状态最优估计。
2 磁罗盘测量系统的滤波模型
2.1 系统状态方程
根据捷联惯性导航理论,磁罗盘测量系统的姿态四元数微分方程为[12]:
(1)
式中:q=[q0,q1,q2,q3]T为磁罗盘姿态四元数;Ω(ω)为反对矩阵,ωi(i=x,y,z)为陀螺测量所得角速率。
若加速度计和地磁传感器在事前已经过标定,这里我们只考虑影响较大的传感器的零偏误差,并假定其误差不变,传感器的零偏误差模型可分别表示为:
(2)
式中:H0=[m0,x,m0,y,m0,z]T用于表示三轴地磁传感器的零偏;而a0=[a0,x,a0,y,a0,z]T即为三轴加速度计的零偏。
如前所述,选取磁罗盘的姿态四元数、加速度计和地磁传感器的常值零偏作为系统状态变量X:
X=[q0,q1,q2,q3,a0,x,a0,y,a0,z,m0,x,m0,y,m0,z]T
因此,综合方程式(1)和式(2)建立磁罗盘测量系统的状态方程,其简写为:
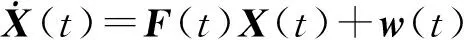
(3)
2.2 系统观测方程
根据磁测姿态解算原理,捷联安装于磁罗盘的三轴地磁传感器测量输出表达式为:
(4)

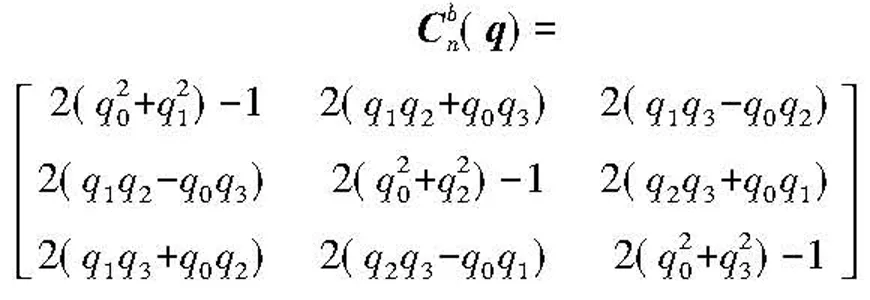
(5)
捷联安装于磁罗盘的三轴加速度计测量输出与重力加速度的关系为:
(6)

若以三轴地磁传感器和加速度计传感器测量输出作为系统的观测信息,则系统的观测变量Z为:
因此,综合地磁传感器测量输出模型(4)和加速度计测量模型(6),建立磁罗盘测量系统的观测方程:

(7)
式中:v(t)为量测噪声,为零均值高斯白色噪声,E[v(t)]=0,E[v(t),vT(τ)]=R(t)δ(t-τ)。
3 磁罗盘抗干扰自适应滤波算法
综合所建立的状态方程(3)和观测方程(7)共同构成磁罗盘测量系统的滤波模型,其简写为:
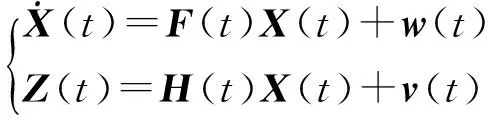
(8)
采用扩展卡尔曼滤波器进行系统的状态估计,对式(8)进行线性与离散化处理后可得:
(9)
考虑到系统采样周期ΔT很短,因此系统状态转移矩阵Φk,k-1可按如下公式计算:
(10)
Φk,k-1进一步整理可得:
(11)
式中:Ω4×4矩阵为:
上述Ω4×4矩阵中,角增量Δθi和Δθ2由式(12)计算所得:
(12)
将观测方程(6)围绕最优状态估计处进行线性化和离散化处理,可得Hk的雅克比矩阵为:
(13)
因此,基于扩展卡尔曼滤波磁罗盘姿态估计算法为:
(14)
要注意利用上述滤波算法进行磁罗盘姿态估计时,认为系统的观测噪声是零均值高斯白色噪声,通常采用传感器的噪声方差来构成量测噪声方差阵Rk:
(15)
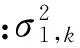
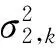
(1)磁罗盘仅受磁干扰时:
(16)
(2)磁罗盘仅受线加速度干扰时:
(17)
(3)磁罗盘同时受两种干扰时:
(18)
即当受两种干扰时,系统的观测量不可信,磁罗盘仪利用陀螺测量数据进行状态的递推计算。
上述式中εa和εh分别为用于判断是否受线加速度干扰和磁场干扰的阈值,而阈值的选取根据所用传感器的精度来具体确定。因此,综合上述受不同干扰时的自适应噪声协方差构造准则(16)~(18)和扩展卡尔曼滤波姿态估计算法(14),可得到磁罗盘抗干扰自适应滤波算法流程如图2所示。

图2 磁罗盘抗干扰自适应滤波算法流程
4 实验验证
为验证磁罗盘抗干扰测量方法实际效果,借助于磁罗盘样机和无磁三轴转台构建半物理仿真平台,如图3所示磁罗盘样机捷联安装于高精度无磁三轴转台,通过控制转台的姿态变化来模拟实际的磁测过程,并由数据采存电路以1 000Hz采样频率完成磁罗盘各传感器测量输出数据的采集与存储,以用于事后的算法验证。

图3 半实物试验实验平台
4.1 磁罗盘静态测量验证
磁罗盘静态测量实验目的是验证不存外界干扰时滤波算法的可行性及解算精度。实验时通过控制无磁转台使磁罗盘处于静态状态,在确保没有引入线加速度和磁场干扰情况下进行磁罗盘静态测量验证。如图4所示为磁罗盘偏航角10°、俯仰角和横滚角2°放置时的静态测量解算结果对比。图4中Δφ,Δθ,Δγ分别表示磁罗盘偏航角误差、俯仰角误差和横滚角误差。
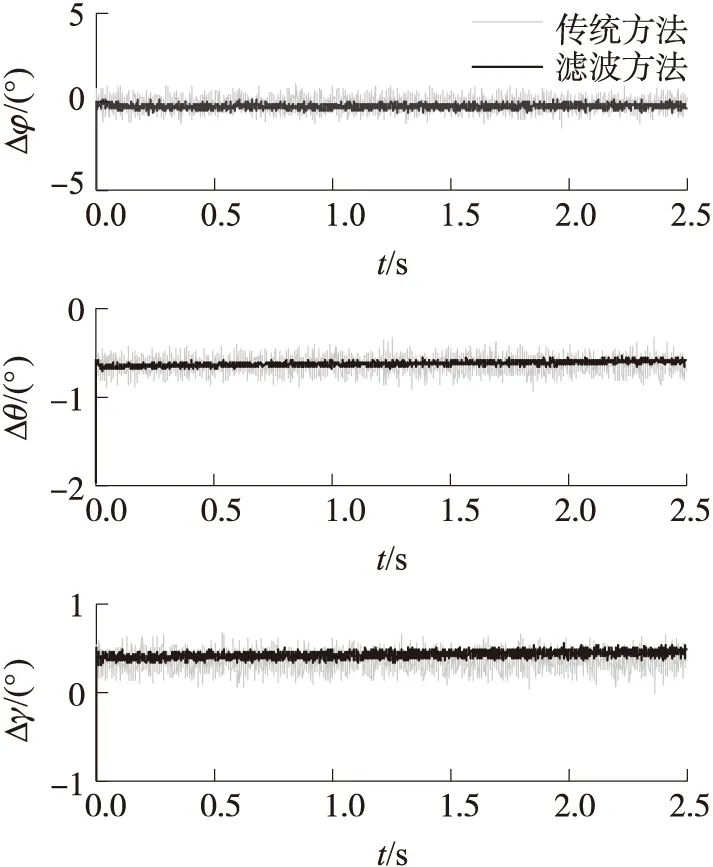
图4 无外界干扰时姿态测量误差
从测量解算结果来看,传统方法测量所得偏航角误差、俯仰角误差和横滚角的均方误差分别为-0.554°、-0.415°和0.486°;而基于滤波方法的偏航角误差、俯仰角误差和横滚角均方误差为-0.434°、-0.322°和0.351°。很明显,在没有受到外干扰情况下滤波方法精度略高些。
4.2 磁罗盘抗干扰动态测量验证
假若磁罗盘在受到不同的外干扰时,仍然具有很高的测量精度,测量误差越小直接反映出其抗干扰动态性能越好。由于评价算法解算精度需要高精度的外参考姿态信息用于对比两种方法的解算误差,所以仍然需要借助于转台进行磁罗盘抗干扰动态实验,因此,在静态测试的基础上,通过在机样周围来回移动磁钢来模拟受外磁场干扰情况;在静态测试基础上通过间断地敲击转台,使捷联于转台的磁罗盘受到外来的加速度干扰,以此来模拟受线性加速度干扰情形;此外,在加入移动磁钢的同时敲击转台以模拟受到两种干扰情形。
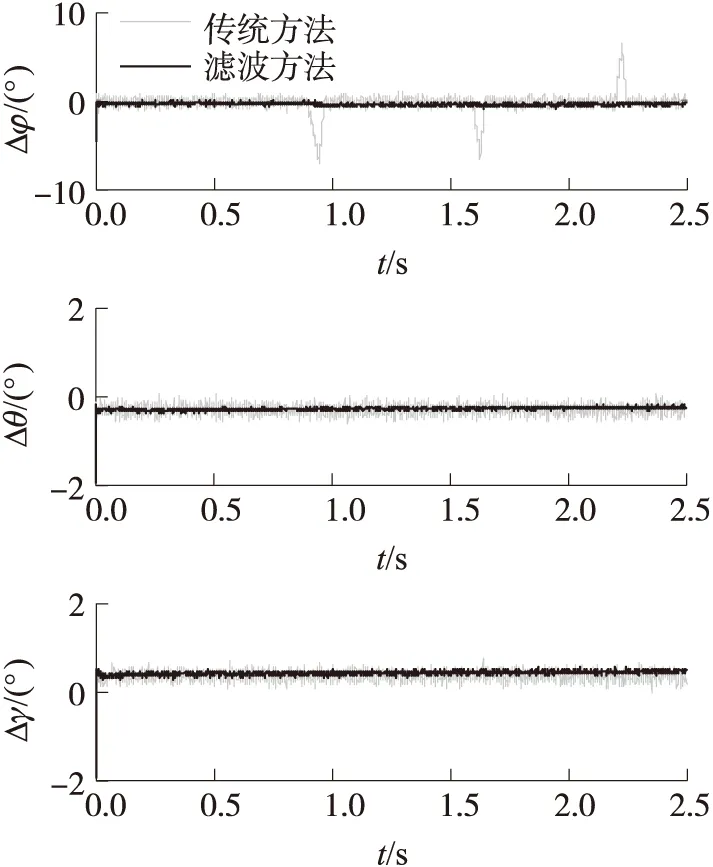
图5 存在磁场干扰时的姿态测量误差
磁罗盘抗干扰动态测试结果如图5~图7所示。其中,图5所示为磁罗盘系统仅仅受到磁钢干扰磁场作用下的测量误差对比。
由于传统测量方法的俯仰角和横滚角是利用加速度计测量信息解算所得,所以,磁场干扰仅仅对偏航角的测量影响明显。在图5中类似于尖脉冲部分即为磁钢干扰时刻,传统方法偏航角解算误差最大为7.8°,俯仰角和横滚角不受影响。而采用滤波方法,存在磁场干扰时的偏航角解算误差均小于0.5°。远远小于前者的7.8°。而俯仰角和横滚角解算精度相当。从结果来看,滤波方法可有效减小磁场干扰的影响。
图6所示为模拟受线性加速度干扰时的姿态角解算误差对比。图中类似突发干扰时刻即为敲击转台加入线干扰时刻。由于存在线加速度有害分量,因此传统方法中俯仰角和横滚角影响最为严重,测量误差达5°,偏航角解算相对影响小些,结果与理论相符合。而滤波方法的磁罗盘姿态角解算所得的偏航角误差、俯仰角误差和横滚角误差均值分别为-0.334 8°、-0.321 3°和0.334 2°,误差方差分别为0.021、0.022和0.033。从结果来看,滤波方法可实现抗线加速度干扰测量。

图6 存在线加速度干扰时的姿态测量误差
图7所示为同时引入磁场干扰和线加速度干扰时的测量误差对比。在受干扰时刻,传统磁罗盘测量方法3个姿态角均会出现很大的测量误差。从结果来看,传统磁罗盘解算方法所解算得的俯仰角、横滚角和偏航角最大误差分别4.5°、4.3°和8.9°;而滤波方法的磁罗盘姿态角解算所得的偏航角误差、俯仰角误差和横滚角误差均值分别为-0.3424°、-0.3451°和0.3678°,误差方差分别为0.022、0.023和0.034。结果表明所述磁罗盘抗干扰滤波方法能够实现外磁场干扰和线性加速度干扰共存应用环境下的准确测量。
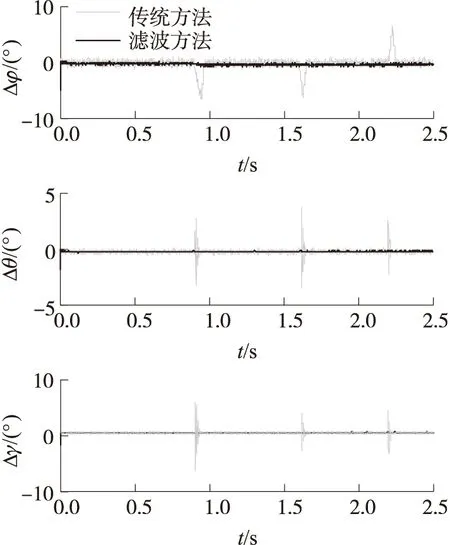
图7 存在两种干扰时的姿态测量误差
5 结论
本文提出了一种基于陀螺辅助的磁罗盘抗干扰测量方法,以解决磁罗盘系统在实际使用过程中不可避免的受到外界磁场干扰和线加速度干扰而引起的严重的姿态测量误差问题。文中重点推导了磁罗盘抗干扰测量滤波算法,借助于磁罗盘样机和无磁三轴转台构建半物理仿真平台,对所设计的基于陀螺辅助的磁罗盘干扰测量算法进行了静态测试和抗干扰动态实验验证以评估算法的静态精度和抗干扰性能分析。实验结果表明了该方法可有效地实现磁罗盘系统的抗干扰测量,且其姿态测量精度能得到进一步的提高。
[1] 范成叶,李杰,陈文蓉,等. 电子罗盘安装误差标定与补偿方法研究[J]. 传感技术学报,2013,26(5):622-626.
[2]李艳,管斌,王成宾,等. 电子磁罗盘航向角误差推导及分析[J]. 仪器仪表学报,2013(7):127-133.
[3]Fong W T,Ong S K,Nee A Y C. Methods for in-Field User Calibration of an Inertial Measurement Unit without External Equipment[J]. Meas Sci Technol,2008(19):185-202.
[4]Fang J C,Sun H W,Cao J J. A Novel Calibration Method of Magnetic Compass Based on Ellipsoid Fitting[J]. IEEE Trans Instrum Meas,2011,60:2053-2061.
[5]Vasconcelos J F,Elkaim G,Silvestre C. Oliveira Pand Cardeira B 2011 Geometric Approach to Strap-down Magnetometer Calibration in Sensor Frame[J]. IEEE Trans Aerosp Electron Syst,2011(47):1293-1306.
[6]万云霞,王言章,程德福. 感应式磁传感器标定磁场处理方法研究[J]. 传感技术学报,2013(4):1309-1313.
[7]晁敏,蒋东方,文彩虹. 磁罗盘误差分析与校准[J]. 传感技术学报,2010,23(4):525-532.
[8]陆建山,王昌明,张爱军. 数字磁罗盘的航向角干扰补偿方法研究[J]. 传感器与微系统,2010(6):75-79.
[9]龙达峰,温晶晶,张晓明. 高速旋转弹捷联磁传感器在线校准方法[J]. 弹箭与制导学报,2014(3):569-571.
[10]蒋窍,李杰,刘俊,等. 基于单片机的GPS/MEMS陀螺仪航向角实时测量系统[J]. 传感技术学报,2011,24(6):919-922.
[11]管斌. MIMU/GPS/磁强计组合导航技术研究[D]. 国防科学技术大学,2010.
[12]秦永元. 惯性导航[M]. 北京:科学出版社,1998.
Anti-Interference Measurement Method of Magnetic Compass Based on Auxiliary Gyroscope
LONGDafeng1,LIUJun1,2*,LIJie1,SUWen3
(1.Science and Technology on Electronic Test and Measurement Laboratory,North University of China,Taiyuan 030051,China;2.Key Laboratory of Instrumentation Science and Dynamic Measurement(North University of China),Ministry of Education,Taiyuan 030051,China;3.Unit 266011 of PLA,Beijing 102600,China)
The acceleration interference and external magnetic field interference will seriously affect the accuracy of the magnetic compass. In order to solve the above problem,this paper presents anti-interference measurement method of magnetic compass based on auxiliary gyroscope. The system filter equations were composed by magnetic compass attitude quaternion differential equations and the sensor error models,and the attitude of magnetic compass was estimated by adaptive Kalman filter. Finally,the semi-physical experiments have carried on by non magnetic turntable. The results show that the method can effectively estimate the attitude of magnetic compass in the magnetic interference and acceleration interference environment. Moreover,the measurement precision of magnetic compass can be improved.
magnetic compass;gyroscope;anti-interference measurement;adaptive Kalman filter

龙达峰(1979-),男,讲师,博士研究生,主要研究方向为地磁、惯性组合导航技术,longdafeng@nuc.edu.cn;

刘 俊(1968-),男,教授,博士生导师,现任中北大学“微纳惯性传感与集成测量”教育部工程研究中心主任,“电子测试技术”国防科技重点实验室(太原分部)主任,“仪器科学与动态测试”教育部重点实验室常务副主任,教育部创新团队带头人,主要从事微米纳米技术、惯性测试技术等方面的研究,Liujun@nuc.edu.cn。
2014-11-24 修改日期:2015-02-07
C:7220;7230
10.3969/j.issn.1004-1699.2015.05.003
TP212.13
A
1004-1699(2015)05-0623-06

