某型舰炮炮口冲击波等压场测试方法
赖富文,张志杰,胡桂梅,张建宇
(1.中北大学仪器科学与动态测试教育部重点实验室,太原 030051;2.中国白城兵器试验中心,吉林 白城 137001)
某型舰炮炮口冲击波等压场测试方法
赖富文1,2,张志杰1*,胡桂梅2,张建宇2
(1.中北大学仪器科学与动态测试教育部重点实验室,太原 030051;2.中国白城兵器试验中心,吉林 白城 137001)
针对现有军标中规定的炮口冲击波等压场测试方法不适用于某型舰炮炮口冲击波压力场的测试情况,提出了以极坐标布放传感器的测试方案,并测试了各点位的冲击波超压值。其次,提出采用三次样条函数方法对测试数据进行插值;最后,使用Delaunay三角划分方法对插值后的数据进行网格划分和等压线绘制,得到了某型舰炮的炮口冲击波等压场。
信息处理技术;炮口冲击波;压力场;等压线;三次样条函数;Delaunay三角网格法
火炮发射时产生的脉冲噪声,由于其突发的高声强和特殊的物理性质,对火炮周围人员、设备和环境都造成不同程度的危害和干扰[1],炮口冲击波场是火炮设计定型试验的勤务性能和安全性能重点考核之一。某型舰炮设计时就需要测试炮口周围的冲击波等压场,为舰炮周围的仪器布放和人员战位提供参考依据。关于炮口冲击波压力场测试,国军标2971—97《火炮安全性和勤务性试验方法》规定在4.5 m×4.5 m矩形范围内,按矩形网格布放100个点位进行炮口冲击波场测试[2]。军标的方法具有以下不足:一是针对牵引式火炮制订,测试区域也只考虑本火炮操作人员的战位,没有考虑周围仪器设备;二是规定的测试区域较小,而测试点位则较多,测试复杂;三是军标中的规定的测试点位不灵活,无法在舰炮上或者周围布放。因此该军标的测试方法不适宜某型舰炮冲击波等压场的测试。本文结合某型舰炮的自身特点,对测试点位布放方法、曲面拟合、网格划分和等压线的绘制等几个方面展开了研究。
1 测试方案及测试结果
1.1 测试点位布置方案
舰炮在舰上的位置是固定的,发射时,由于其射向的变化,周围的仪器设备与炮口相对位置是不固定的,要求测试舰炮的炮口冲击波超压分布。火炮发射时,高速高压火药气体出膛口后形成的冲击波具有较强的指向性,不同方向辐射能量有较大的差异,同一径线上不同距离点的冲击波超压值随距离呈指数衰减,因此,本测试方案按照极坐标方式布放,在不同径向上不同距离放置测试传感器[3]。某型舰炮属于小口径,炮口冲击波对周围操作设备影响范围较小,火炮射击时,考虑到炮口左右对称,选择一侧进行测试。由于炮口正前方是弹道方向,后方是炮身,不利于布放传感器。因此,以射击向为0°,选择120°~240°弧线范围,每隔30°布放。测试径向范围为3 m~7 m,每隔1 m布放一个,即同条径向布放5个点位,共布放25个点位,具体点位布放如图1所示。
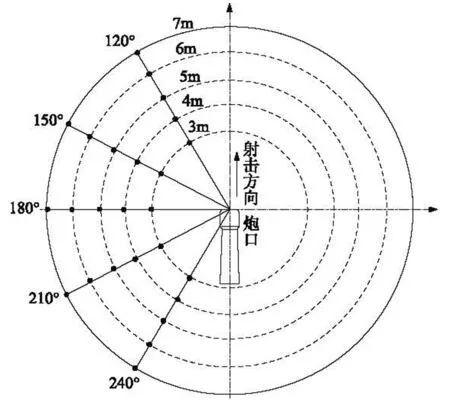
图1 某型舰炮炮口冲击波场测试点位布放图
1.2 各点位冲击波测试结果
炮口冲击波测试时要求压力小于6.9 kPa采用电容传声器,不小于6.9 kPa采用压力传感器。压力传感器要求:谐振频率不低于75 kPa,上升时间不大于20 μs,直径应小于6 mm。电容传声器要求:声压级线性动态范围上限不低于172 dB,上升时间不大于18 μs,频响0.02 kHz~70 kHz(优于±2 dB)[4-6]。该型舰炮的炮口压力值较小,结合炮口压力对测试传感器指标要求,试验选用ENDEVCO公司8510B-5型压阻式压力传感器和B/K公司4938型电容传声器。在120°、150°径向上所有点以及180°、210°径向上3 m、4 m上的点布放压力传感器,其余点位布放电容传声器。测试时,传感器与炮口同高,传感器敏感面垂直向上,测试掠入射冲击波,火炮射角射向都为0°,采样频率为2 MHz,各点位具体测试结果见表1。图2为120°径向上3m处的原始压力曲线图,图3为240°径向上3 m处的原始压力曲线图。

表1 各测试点位具体测试结果 单位:kPa

图2 120°径向3 m处的原始压力曲线
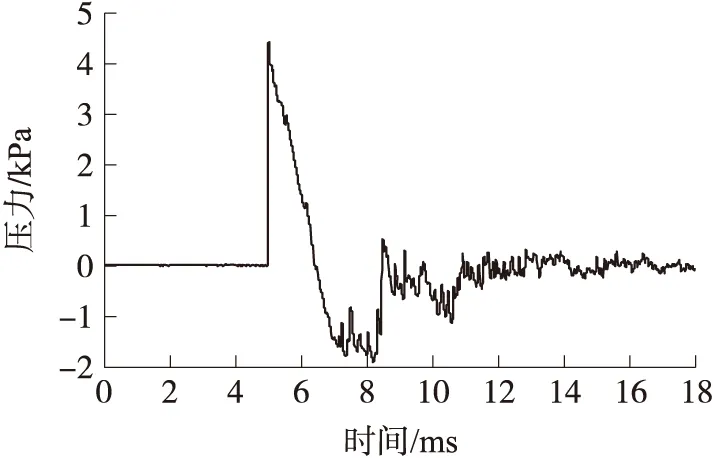
图3 210°径向3 m处的原始压力曲线
2 炮口冲击波等压场曲面绘制
2.1 三次样条函数的插值方法
三次样条函数不仅光滑性好,而且能够保证拟合曲线一阶、二阶导数的连续性。因此选用三次样条函数进行冲击波压力场曲面插值。三次样条函数是按一定光滑性要求对接起来的分段多项式,根据三次样条函数的原理[7-8],给出三次样条插值具体方法。
已知插值条件下曲线上的一组型值点{Vi},其中i=1,2,…,n,Vi的坐标为(xi,yi)。序列x0,x1,…,xn属于区间[a,b]。若函数y(x)是区间[a,b]上的分段三次多项式,并且满足下面两个条件:
①在区间[a,b]上二阶连续、可导;
②y(xi)=yii=1,2,…,n,
则称y(x)为区间[a,b]上序列x0,x1,…,xn的插值三次样条函数,xi为三次样条函数的节点。
给定一组型值点(xi,yi),i=1,2,…,n,mi为型值点(xi,yi)处的斜率,则j段三次样条函数表达式为:
yj(x)=ajx3+bjx2+cjx+djj=1,2,…,n
(1)
令hj=xj-xj-1,插值函数系数aj,bj,cj,dj的求解方程式为:
(2)
mj可通过连续条件和端点条件求出,求解方程组的矩阵形式:

(3)
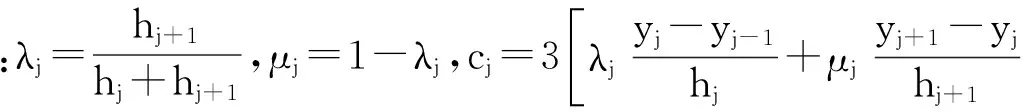
2.2 冲击波压力曲面绘制结果
采用极坐标测试冲击波压力场时,得到的是以半径和角度的二维离散数据组,曲面插值绘制时,先在径线上,然后在弧线上分别采用三次样条函数进行插值,可以得到炮口冲击波压力场曲面。图4为某型舰炮的炮口冲击波压力场曲面。
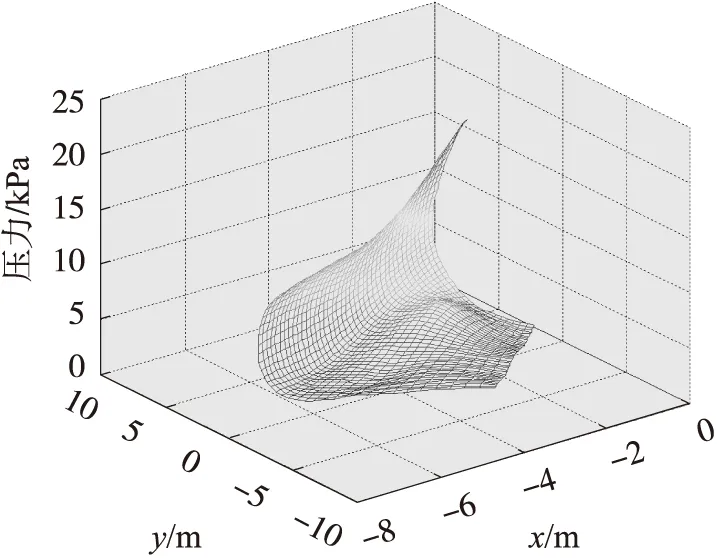
图4 某型舰炮炮口冲击波压力曲面
3 等压线的绘制
炮口冲击波压力场测试数据是一些离散点,要得到等值线首先要用插值的方法得到等值点,再把它们联接成等值线。常规的等值线绘制方法有矩形网格法和三角形网格法两种[9],但是极坐标点布置测试的数据组在平面坐标上表现不规则的离散点,因此采用三角网格划分法来实现等压线的绘制。绘制网格等压线的步骤一般为:离散数据网格化,网格点数值化,等值点的计算,等值线追踪,光滑和标记等值线[10]。
3.1 三角网格划分
三角网格划分法选用Delaunay法,它是利用不规则三角网建立数字高程模型的一种优化算法,基本思想是:生成一个满足剖分要求的三角形,然后分别扩展该三角形的3个边,生成新的三角形。接下来对新的三角形进行扩展,直到扩展完毕,从而生成满足要求的三角形剖分网格[11]。炮口冲击波压力场测试时,测试点的坐标为极坐标,因此在三角划分时需将极坐标转换成直角坐标。直角坐标原点为炮口在地面投影。对插值后的某型炮口冲击波等压场测试数据点进行三角形网格划分结果如图5所示。

图5 Delaunay三角形网格划分结果
3.2 等值线的绘制
3.2.1 等值点确定
对于值为Zc的等值线,三角形棱边kj之间存在等值点的条件是
(Zj-Zc)×(Zk-Zc)≤0
(4)
若Zk-Zc和Zj-Zc等于零,则等值点一定通过k或j点,此时不利于下一步等值点的追踪,因而需要做简单处理,取Zk=Zk-ε或Zj=Zj-ε,ε为很小的正数,使等值线在充分靠近Zk和Zj的网格点附近通穿过[11-12]。图6为三角形网格等值线的几种走向。

图6 三角形网格等值线的几种走向
对于任意三角形,若有棱边满足条件式(4),一定有等值线穿过此三角形。按照式(4)对所有三角形遍历,则可求出某条等值线的单元总数和有该等值线穿过的单元棱边。如果棱边kj存在量值Zc的等值点,则等值点坐标可应用以下线性插值公式获取:
(5)
3.2.2 等值线追踪
等值线追踪步骤如下:
①首先对等值线Zc用式(4)对区域内所有单元进行遍历,记录等值线穿过的单元数、两条特征棱边和各自边的等值点坐标。
②判断所有等值线穿过的单元棱边集合中所有的棱边是否有边界。
③在所有等值线穿过的单元内追踪,追踪依据为等值线游动必然穿过共棱边且有等值线穿过的单元。
3.2.3 等压线绘制结果
某型舰炮炮口冲击波等压线Zc的取值范围:从3 kPa到10 kPa,每隔0.5 kPa,10 kPa到19 kPa,每隔1 kPa,共24条等压线,采用上述方法绘制结果如图7所示,图中坐标点(0,0)为炮口位置。

图7 某型舰炮炮口冲击波场等压线
4 结论
①针对现有国军标规定的布点方案不适宜某型舰炮炮口冲击波压力场测试,提出了以炮口为圆心,在炮口一侧,以极坐标布放传感器的测试方案。
②采用了三次样条函数的插值方法,对测试数据进行了曲面插值,得到了炮口冲击波场的压力曲面。
③针对极坐标布点方案,采用了Delanuay三角形网格划分法进行网格划分,并绘制了炮口冲击波场等压线。
④本文中的测试方法可以推广应用于其他火炮炮口冲击波压力场测试中。
[1]王秉义.火炮脉冲噪声特性与爆炸声的特性和防治[M].北京:国防工业出版社,2001:31-32.
[2]濮永贵.GJB 2971—97 火炮安全性和勤务性试验方法[S].北京:国防科学技术工业委员会,1997.
[3]赖富文,张建宇,霍李.某型坦克140 dB噪声等压线测试方法研究[J].兵器试验,2010(5):23-27.
[4]孙忠良.对军标“炮口冲击波超压传感器技术要求”的分析[J].传感器技术,1992,(3):28-32.
[5]刘江,孙忠良,梁之安,等.GJB 2A—1996 常规兵器发射或爆炸时脉冲噪声和冲击波对人员听觉器官损伤的安全限值[S].北京:国防科学技术工业委员会,1996.
[6]孙忠良.GJB 349.28《常规兵器试验方法:炮口冲击波超压测试》[S].北京:国防科学技术工业委员会,1990.
[7]简弃非,刘海燕.SnO2纳米传感器的灵敏度-温度特性曲线拟合研究[J].传感技术学报,2005,18(1):50-52.
[8]陈文略,王子羊.三次样条插值在工程拟合中的应用[J].华中师范大学学报(自然科学版),2004,38(4):418-422.
[9]朱心雄.自由曲线曲面造形技术[M].北京:科学出版社,2000:215-220.
[10]林丽娜.油田等值线图形绘制方法与应用[D].长春:吉林大学数学学院,2005.
[11]徐旭.基于三角网的等值线生成及填充算法[D].长沙:中南大学信息科学与工程学院,2011.
[12]何俊,王梦麟.基于Delaunay三角网的二维电磁态势可视化方法[J].系统工程理论与实践,2011,31(9):1798-1802.
A Method to Measure Muzzle Shock Wave Pressure Field for A Naval Gun
LAIFuwen1,2,ZHANGZhijie1*,HUGuimei2,ZHANGJianyu2
(1.Key Laboratory of Instrumentation Science and Dynamic Measurement,North University of China,Taiyuan 030051,China;2.Baicheng Ordnance Test Center of China,Baicheng Jilin 137001,China)
According to the muzzle shock wave measurement method provided by existing military standard is not suitable for a certain type of naval gun,the measurement scheme based on polar coordinates distributed sensors was presented,and the muzzle shock wave overpressure of each position was measured.Secondly,the interpolation curve pressure field was achieved using Cubic spline interpolation function.Finally,the drawing method of contour line based on Delaunay triangulation was adopted,and obtained the muzzle pressure field of a certain type navel gun.
information processing technology;muzzle shock wave;pressure field;contour line;cubic spline interpolation function;Delaunay triangulation

赖富文(1973-),男,四川邻水人,中国白城兵器试验中心高级工程师,中北大学仪器与电子学院博士研究生。主要研究方向为数字信号处理及嵌入式系统,laifuwen0106@163.com;

张志杰(1965-),男,山西太原人,中北大学仪器与电子学院教授,博士生导师,主要从事动态测试理论、技术与应用,信号处理理论与技术以及通信与信息系统方面的研究,zhangzhijie@nuc.com.cn。
2014-08-02 修改日期:2014-11-07
C:7320Z
10.3969/j.issn.1004-1699.2015.01.014
TJ306
A
1004-1699(2015)01-0077-04

