一种基于自适应RSSI测距模型的无线传感器网络定位方法*

杨文铂,邢鹏康,刘彦华

(河南工业职业技术学院电子工程系,河南 南阳 473000)



一种基于自适应RSSI测距模型的无线传感器网络定位方法*

杨文铂,邢鹏康,刘彦华*

(河南工业职业技术学院电子工程系,河南 南阳 473000)

为了提高无线传感器网络的节点定位精度和环境适应性,研究了环境因素及信道噪声对无线信号传输特性的影响,对测量误差进行修正,得到精确的环境自适应RSSI测距模型,在此基础上结合距离加权修正的改进WELSE算法,得到了一种新的混合定位算法。在ZigBee平台CC2430上的测试结果表明本算法在未知环境中不需要预整定模型参数,在定位精度上,本文算法相比WELSE提高了49%,比WCLA提高了36%,可见其具备优秀的环境适应性和较高的定位精度。

WSN;节点定位;RSSI测距;环境自适应;WELSE

在无线传感器网络(WSN)应用中,节点的位置信息很重要,在大量的应用中,不知道传感器节点位置的感知数据是没有意义的。WSN的定位算法按其实现方式可分为基于外部实现的和基于自身实现的两类。其于外部实现的是指需要WSN外的GPS、人工等辅助获取坐标的方法;基于自身实现的定位是指其定位过程完全在内部完成。基于外部实现定位的方法,定位区域有一定局限性。为了获得更好的适应性,基于WSN自身实现的定位方法成为必然的选择。WSN内的节点按位置关系可分为定位节点和锚节点。定位节点(Blind Node)即待确定坐标的节点,可以是固定的也可以是移动的;锚节点又称之为参考节点(RefNode),是固定好位置并预设好坐标的节点。基于WSN自身实现的定位算法主要是利用定位节点与锚节点的相对位置关系,根据锚节点的坐标计算出定位节点的实际坐标,这个过程一般需要多个锚节点参与。根据定位算法是否依据测量到锚节点的距离或角度分为:距离相关(range-based)的定位算法和距离无关(range-free)的定位算法[1]。前者较有代表性的是极大似然估计算法，后者较有代表性的是质心算法。通常距离较远的锚节点信息对定位贡献的误差较大,距离较近的锚节点误差较小。为使定位获得较高的精度,偏向于较近节点提供的位置信息,需要引入距离权值来修正上述算法。对质心算法,引入修正后变为加权质心算法(WCLA)[2],实质上演变为距离相关算法。极大似然估计法引入修正后成为加权极大似然估计算法(WELSE)[3]。上述算法虽然原理不尽相同,但在定位过程中都需要准确的测距模型来提供定位计算的距离参数。距离相关定位算法需要利用TDOA或TOA、AOA[4]、无线信号强度指示(RSSI)等技术对定位节点到锚节点的距离进行测量。RSSI测距技术主要是是利用无线信号强度衰减率与距离的关系进行测距[5],因传感器节点本身具有通信能力,所以无需增加任何额外的硬件设备,故基于RSSI测距的定位算法是最为简单、成本低廉的,成为目前研究的热点。

本文提出了一种基于环境自适应RSSI测距模型的混合型定位算法,精度高于WELSE及WCLA定位算法。

1 测距模型及特性分析

对于RSSI测距,寻找准确的RSSI-距离关系模型对于定位的精度是关键。常见的RSSI-距离模型有自由空间传播、两径反射、Shadowing、哈它等。在实际中更具综合性的Shadowing经验模型[6]得到了更为广泛的应用(见图1)。Shadowing模型由式(1)给出:

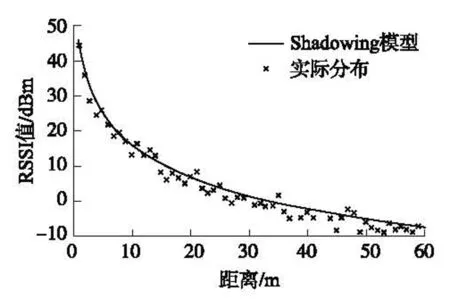
图1 Shadowing模型

PL(d)=PL(d0)-10nlg(d/d0)+Xσ

(1)

式(1)中,d为接收端到信源的距离,d0为参考距离,PL(d)为接收信号强度(dBm),PL(d0)为在参考距离处的信号强度,n为传播系数,反映信号随距离的衰减速率,Xσ为均值为零的信道白噪声,在上述模型中PL(d0)和n参数都要通过实地测量确定。在应用中通常取参考距离d0为1m处的信号强度值PL(1),此值记为常数A[7],所以式(1)可变换为如下形式:

PL(d)=A-10nlgd+Xσ

(2)

相关研究表明,信号强度与距离存在对应关系,信道噪声是构成模型不确定性的主要来源。Shadowing模型在实际应用中主要存在如下问题导致其环境适应性较差:①Shadowing模型参数不能自整定,需要在定位区域进行预测量以获取PL(d0)和n参数;②Shadowing模型虽然考虑到了环境影响因素,但是由于在定位范围不同区域的多径反射、温湿度等衰减特性不尽相同,难以满足实际多变的环境特性而带来较大的模型误差。

由于多径反射、温湿度等带来的传播系数变化在室内、矿井等环境内是十分普遍的,难以用滤波的方式加以消除,如果所有区域使用相同的模型参数,整体上会带来较大的测距误差。为了提高测距模型的环境适应性,环境自适应的定位算法的核心在于由不同区域锚节点分别辨识出其适应于本区域的测距模型,辨识过程是在线进行的,因此可以实现定位算法的环境自适应。

2 自适应RSSI测距模型

2.1 自适应测距模型的构建

首先获取当前锚节点接收到的相邻锚节点坐标值及信号强度值r,然后建立以r为自变量的待定系数m次多项式,r的函数y(r)代表当前锚节点到相邻锚节点的距离,得到下面的测距模型(式(3)):

y(r)=α0+α1r+α2r2+…+αmrm

(3)

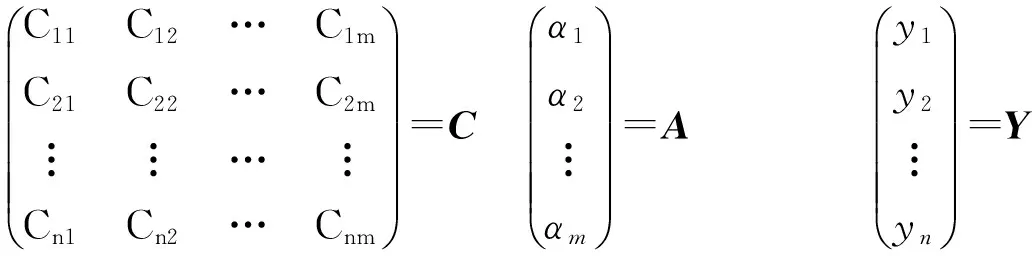
将当前锚节点接收到的n个(n>m)相邻锚节点信息后代入上式,得到如下方程组:

其中系数α1,α2,…,αm待定,然后使用多项式加权最小二乘拟合,求解出待定系数。

2.2 自适应测距模型的辨识

确定y(r)表达之后,以当前锚节点与邻锚节点的实际距离y与由测距模型得到的距离y(r)之差的平方和最小为条件来选择y(r)中的系数。实际距离由坐标关系计算得到:

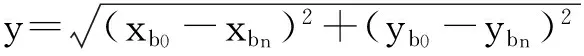
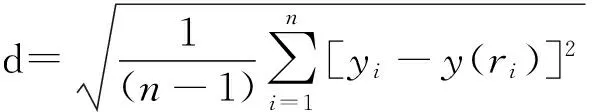
Prcv(d)=Prcv(d0)·(d0/d)λ=C·(1/d)λ

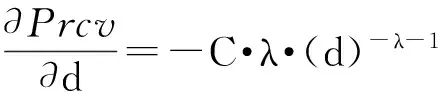
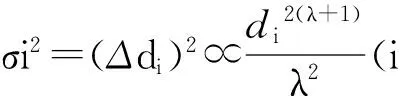
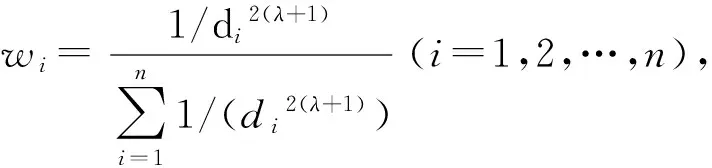
2.3 环境自适应测距模型(SDM)测试

首先通过实测以获取实际环境中RSSI-距离关系数据。将Tx节点固定,每间隔1 s发射一次信号,Rx节点每间隔1m距离读取RSSI值。在每个距离测试点Rx连续读取20组RSSI数据取平均,以滤除随机干扰影响。通过实测获得了3种室内环境和3种室外环境在不同温湿度条件下的多组数据。Tx和Rx节点采用符合IEEE802.15.4/ZigBeeTM规范的的CC2430模块[12],天线增益10dBi,无线协议栈软件采用ZStack-1.4.3-1.2.1。

为了研究场地特性对信号传播特性的影响,在上述实测数据中选取了同种温湿度条件下的三块不同的室内场地(IE1-3)数据。为了研究温湿度条件对信号传播特性的影响,选取了同一块场地(EE1)的三组温湿度数据。从图2看到,不同的场地对传输曲线的中近端(0～12 m)范围的影响较大,对远端的影响较小,室内环境影响主要是反射和遮挡等因素。从图3看,温度-湿度因素对传输曲线也有较大的影响,在高温、高湿环境下,信号的衰减显著增大。

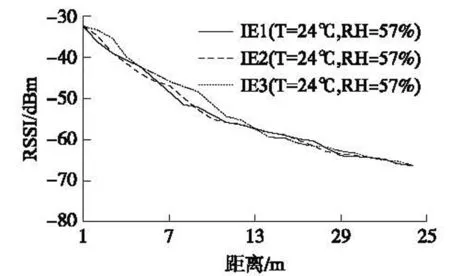
图2 场地对传输特性影响

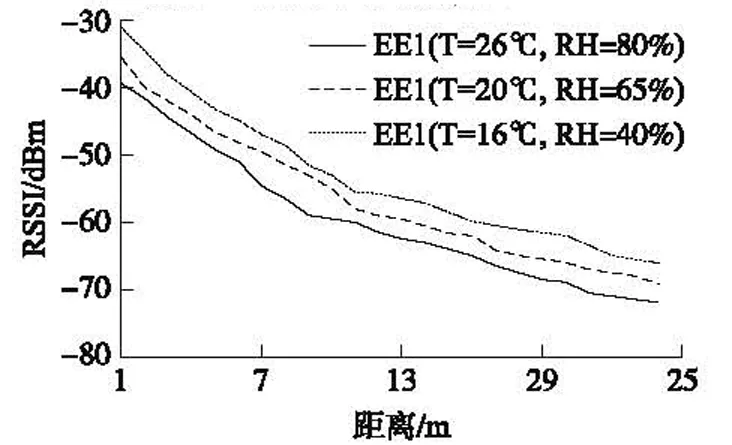
图3 温湿度对传输特性影响

本文随机选择了五组不同环境实测数据(EE1～EE5),来测试测距模型(SDM)效果,使用三次多项拟合,选择了Shadowing曲线(式(2)确定)作为对照组。式(2)中的A参数通过现场测量得到。为了消除天线方向性影响,将发射节点(Tx)置于原点,将接收节点(Rx)置于半径为1 m的圆周上(见图4),正对源节点,每隔45°弧长进行一次测量,每次测量值取20组RSSI值的平均,最后对各次测量求平均得到A参数[13]。经验曲线的N参数通过与实测数据的拟合得到。5种环境下分别测量以取得各自的A和N参数。Shadowing曲线可由两种拟合方式得到:通过最小二乘拟合得到曲线LS或通过距离加权最小二乘拟合得到曲线WLS。图5展示了在第1个测试环境(EE1)下的LS、WLS、SDM拟合效果对比。通过对5种环境(EE1～EE5)的测试(见图6),LS的平均测距误差为1.87 m,WLS为1.29 m,SDM为0.12 m。在上述测距算法中,SDM取得了最高的测距精度,而且不需要预整定模型参数,实现了环境自适应。

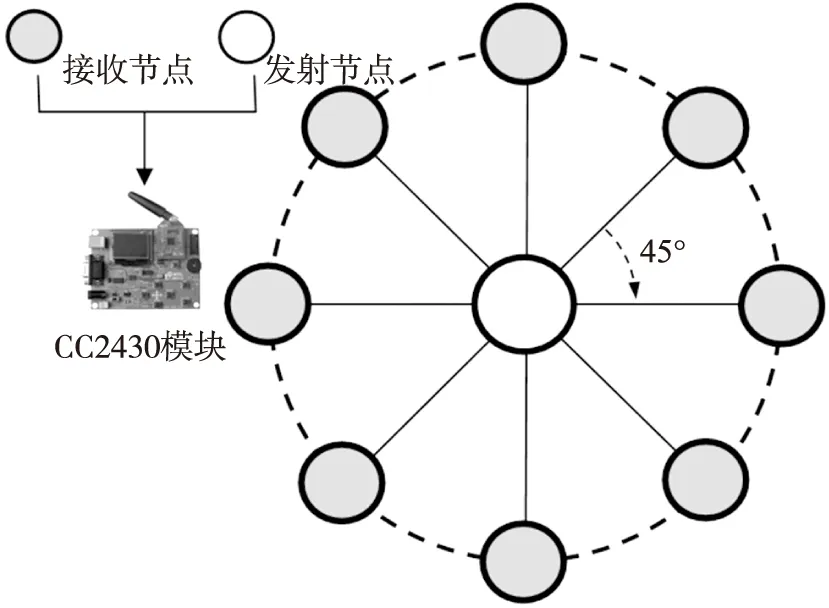
图4 Shadowing的A参数获取

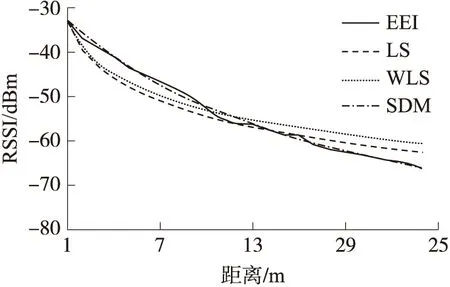
图5 拟合曲线对比

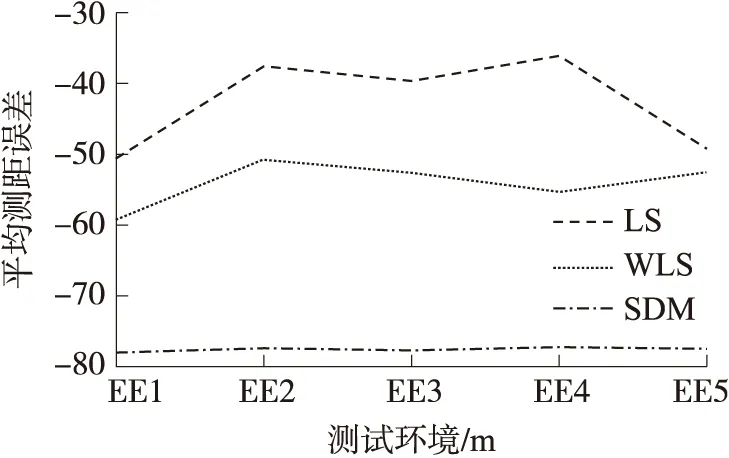
图6 测量误差对比

3 改进后的混合自适应定位算法

如2.2小节所述,各节点的距离测量误差是异方差性的,需要引入距离权值进行修正。在WLSE中,距离权值取距离的倒数,不够准确。在本文的测距模型中,对距离权值进行精确的求解得到权值矩阵W。然后在WLSE上引入修正后的权值矩阵W,获取定位误差的无偏估计,得到改进加权极大似然估计定位算法(EWLSE),具体算法如下:

设有n个锚节点Rf1(xb1,yb1)、Rf2(xb1,yb1)、…、Rfm(xb1,yb1)。d1、d1、…、dn分加别为定位节点到各锚节点的距离。根据距离关系有:

解得:X=(ATWA)-1AWB

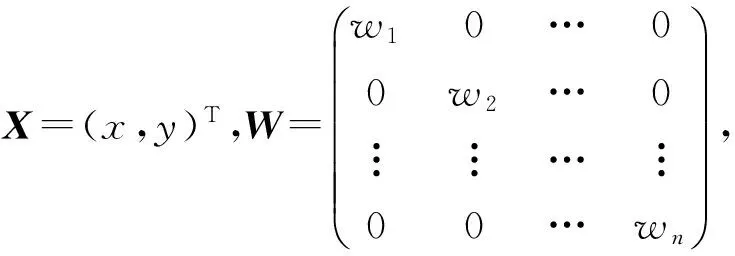
SDM和EWELSE结合,得到了一种基于自适应测距模型的混合定位算法HSLA(HybridSelf-adaptedLocationingAlgorithm)。为了测试HSLA算法的效果,选取了极大似然估计(LSE)、WELSE和WCLA定位算法作为对比,使用MATLAB进行仿真。为了模拟实际环境的不确定性,所有节点在定位范围内随机分布,节点A参数取1m处能量均值-33dBm上下20%范围(-50.4～-33.6)内随机值,n参数取一般环境范围(2～5)内的随机值。对于LSE、WELSE和WCLA使用经验算法(式(2)),A参数使用固定均值-33,n参数取环境均值3.5,利用式(2)算法进行测距,HSLA利用自适应测距模型进行测距。仿真结果如图7和图8所示。

从图7可以看到,定位精度随着锚节点数量的增加而提高,同时最大定位误差会降低。HSLA的平均定位误差比WELSE的小49%,比WCLA的小36%。从图8中可以看,HSLA的最大定位误差比WLSE小41,比WCLA小22%。WELSE比LSE有着更好的定位精度,显示出距离权值在提高定位精度中的明显作用,而HSLA通过自适应测距模型得到的最优距离权值具有更好的效果。整体测试结果表明,HSLA具有在传播特性非均一的未知环境中具有最高的定位精度。

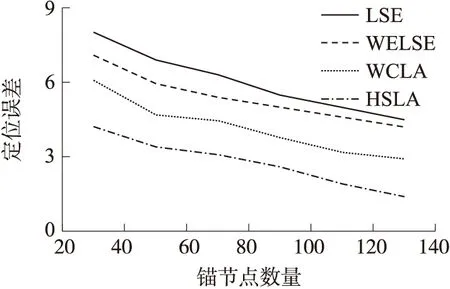
图7 平均定位误差

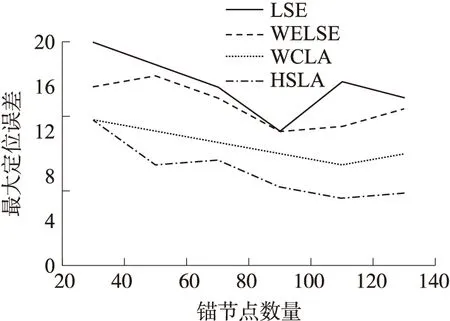
图8 最大定位误差

4 结束语

本文针对实际定位环境不确定性因素带来的测距误差问题引入了基于环境自适应测距的混合定位方法(HSLA)。使用加权最小二乘法辨识出所在环境的测距模型,这个过程是在线进行的,可以避免经验模型中预整定参数导致的环境误差。在HSLA中为了降低测距噪声带来的定位误差,研究了噪声的特性、与测距距离的关系,根据无偏估计原则构造出改进WELSE中的距离权值。测距实验表明该算法对不同环境具有自适应性,并达到了较高的精度。计算机仿真证明本文定位算法具有良好的环境适应性和较高的精度。从实验结果看,该定位算法符合一般性应用场合,具备普遍意义。

[1]陈锡剑,程良伦.基于RSSI的功率匹配定位算法的研究与实现[J].传感技术学报,2013,26(5):709-714.

[2]王新芳,张冰,冯友兵.基于粒子群优化的改进加权质心定位算法[J].计算机工程,2012,38(1):90-95.

[3]徐原博,钟丽鸿,崔洋,等.基于无线传感器网络的极大似然定位法的分析[J].传感器与微系统,2011,30(10):37-43.

[4]Girod L,Estrin D.Robust Range Estimation Using Acoustic and Multimodal Sensing[C]//IEEE,eds.Proceedings of IEEE/RSJ International Conference on Intelligent Robots and Systems(IROS01).Maui,USA:IEEE,2001:1312-1320.

[5]方震,赵湛,郭鹏,等.基于RSSI测距分析[J].传感技术学报,2007,20(11):2526-2530.

[6]朱明辉,张会清.基于RSSI的室内无线网络定位技术研究[J].现代电子技术,2010(17):45-48.

[7]张娇.基于接收信号强度的定位算法的研究[D].沈阳:东北大学信息科学与工程学院,2010.

[8]陈良泽.用矩阵运算实现曲线拟合中的最小二乘法[J].传感技术,2001,20(2):30-34.

[9]高国胜,陈俊杰,李刚.基于RSSI测距的信标节点自校正定位算法[J].测控技术,2010,28(8):93-97.

[10]何晓群,刘文卿.浅谈加权最小二乘法及其残差图[J].统计研究,2006(4):53-57.

[11]Rappaport T S.Wireless Communication Principles and Practice.Upper Saddle River:Prentice Hall PTR,1996:70-74.

[12]TI/Chipcon.CC2430 Prelimin Data Sheet(rev.2.1)SWRS036F[DB/OL].http://www.ti.com/lit/ds/symlink/cc2430.pdf,2007-05-30.

[13]章坚武,张璐,应瑛.基于ZigBee的RSSI测距研究[J].传感技术学报,2009,22(2):285-288.

A Positioning Method of WSN Based on Self-Adapted RSSI Distance Model*

YANGWenbo,XINGPengkang,LIUYanhua*

(Electroincs Department,Henan Polytechnic Institute,Nanyang Henan 473000,China)

In order to improve the adaptability and precision of wireless positioning technology of the nodes in WSN,we first analyzed the effects of environmental factors and channel noises on the characteristics of signal transmission and then get the accurate RSSI distance measurement model of environment adaptive.On the base of the distance model and improved WELSE alghorithm with distance weighted correction,we get a new hybrid positioning algorithm of WSN.The tests on the CC2430 platform show that in unknown environments there is no need to calibrate algorithm parameters in advance and the accuracy of positioning is increased by 49% compared to WELSE and by 36% compared to WCLA.The results prove that,the algorithm is well environment adaptive with high precision.

WSN;node positioning;RSSI distance measurement;environment adaptive;WELSE

杨文铂(1981-),男,汉族,河南南阳人,工学硕士,河南工业职业技术学院电子工程系讲师,主要研究方向为无线传感器网络和嵌入式系统,wenbostd@126.com;

邢鹏康(1984-),男,汉族,陕西西安人,工学硕士,河南工业职业技术学院电子工程系讲师,主要研究方向为物联网技术及应用;

刘彦华(1977-),女,汉族,河南新乡人,河南工业职业技术学院电子工程系副教授,工程硕士,主要研究方向为智能控制技术,lyhqxi@163.com。

项目来源:河南省科技攻关项目(142102310225)

2014-08-21 修改日期:2014-11-12

C:5210C;7310N

10.3969/j.issn.1004-1699.2015.01.024

TN98

A

1004-1699(2015)01-0137-05