AFM压电陶瓷驱动器类Hammerstein建模与参数辨识*
徐运扬,徐康康,沈 平
(中南大学高性能复杂制造国家重点实验室,长沙 410012)
AFM压电陶瓷驱动器类Hammerstein建模与参数辨识*
徐运扬,徐康康,沈 平*
(中南大学高性能复杂制造国家重点实验室,长沙 410012)
AFM(Atomic Force Microscope,原子力显微镜)中的压电陶瓷驱动器具有率相关迟滞非线性特性,这会影响AFM的扫描和定位精度。针对传统静态迟滞模型不能反映系统率相关动态迟滞特性的缺陷,提出Hammerstein模型以描述压电陶瓷驱动器的静态和动态迟滞特性。利用最小二乘支持向量机结合奇异值分解法对模型中的参数进行辨识。实验结果表明,模型能体现压电陶瓷驱动器的率相关迟滞特性,精度高于传统静态迟滞模型,建模方法对此类系统具有较好的应用价值。
压电陶瓷驱动器;非线性建模;Hammerstein模型;系统辨识;支持向量机
AFM中的压电陶瓷驱动器是扫描和成像系统中的关键部件[1],其响应速度快,具有纳米级的定位精度。但同时其输入输出表现为非光滑、多值映射的迟滞回环特性,即同一个输入电压值可能对应多个输出位移[2],若不对迟滞进行补偿,则会影响AFM扫描和定位精度,导致成像的畸变。因此,研究这种非线性关系并建立其准确的模型,并对迟滞加以补偿,对提高压电陶瓷驱动器的运动控制精度具有重要的意义。
对压电陶瓷驱动器的迟滞建模,国内外学者做了大量的工作。如基于Preisach模型的建模方法[3],虽然能较好地描述压电陶瓷驱动器的迟滞非线性特性,但模型结构复杂,建模过程需要大量特定的实验,实际应用不便。另外还有PI(Prandtl-Ishlinskii)模型[4],虽也能描述迟滞非线性,但由于其算子关于原点奇对称而实际迟滞曲线大都是非对称的,这会引入建模误差,影响模型精度。其他的智能建模法,如神经网络[5],受限于算法本身,存在局部极小值点,容易陷入过训练,且网络结构、类型的选择过分依赖于经验,这都会影响模型的预测效果。以上模型均属于静态模型,实际上压电陶瓷驱动器的驱动电压和输出位移间还存在率相关迟滞非线性特性[6],即迟滞的程度同输入电压的频率有关。这说明压电陶瓷驱动器的迟滞特性同时包含静态非线性和线性动态特性[7]。因此有必要对模型的形式加以改进,以提高模型的精度。
Hammerstein模型是一类块结构的非线性动态模型[8],这类模型由线性动态模块和非线性静态模块组成,其已被证明能描述一大类非线性系统[9]。模型简单,参数辨识容易。受此启发,本文提出基于Hammerstein模型的压电陶瓷驱动器迟滞模型,这种模型能描述压电陶瓷驱动器的静态非线性以及动态特性,并具有较高的预测精度。
对Hammerstein模型参数辨识的研究,Krzyzak[10]等使用递推核回归法和协相关法辨识Hammerstein模型的参数,对模型的线性部分使用协相关系数求解,模型的非线性部分由递推核回归法得到。Chen[11]等提出递推最小二乘法辨识对模型参数进行辨识。向微[12]等将线性动态部分和非线性静态部分分别用Laguere级数和非线性基表示,辨识得到两部分的参数。Pelckmans和Goethal等[13]把最小二乘支持向量机LS-SVM(Least Squares Support Vector Machine)用于Hammerstein模型参数的辨识,通过采用冗余参数法以及增加约束,辨识得到了线性部分和非线性部分的系数。由于最小二乘支持向量机能很好地表示非线性过程[14],且其参数具有冗余性,因此,本文采用最小二乘支持向量机算法,通过增加约束条件,结合奇异值分解,辨识Hammerstein模型中的参数。实验结果表明,率相关迟滞Hammerstein模型能体现系统输出与输入信号频率间的动态特性,较传统静态迟滞模型更能体现压电陶瓷驱动器的真实特性。
1 问题构造
AFM压电陶瓷驱动器的输入输出特性包含静态非线性以及线性动态特性,可用Hammerstein模型进行描述[7]。静态非线性部分体现系统的静态迟滞非线性,动态部分体现系统的率相关动态特性。
Hammerstein模型是一类块结构的非线性动态模型,它由一个静态非线性环节和一个动态线性环节串联组成。压电陶瓷驱动器Hammerstein模型的结构如图1所示。
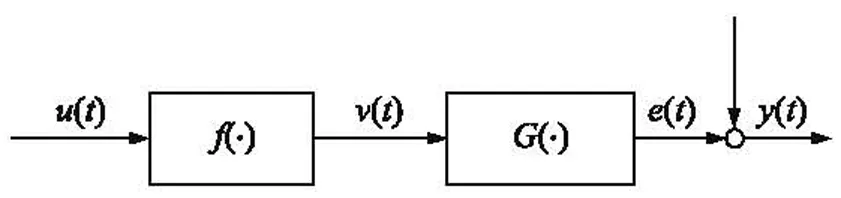
图1 Hammerstein模型结构图
u(t)代表t时刻的输入电压,它经过静态迟滞非线性模块f(·)得到中间变量v(t),该变量再经过线性动态模块G(·),同e(t)叠加后得到t时刻的位移输出y(t),其中e(t)代表未建模的系统特性和随机扰动。
对压电陶瓷驱动器而言,其某一时刻的输出与历史电压变化以及位移变化情况有关,其输入输出关系能用以下基于Hammerstein结构的方程表达[9]:
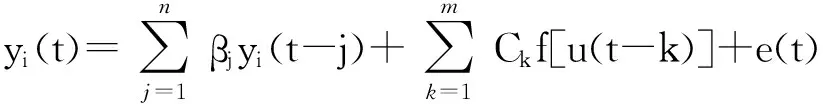
(1)
其中u(t)=[u1(t),…,unu(t)]T表示输入电压信号,yi(t)表示输出位移值,m,n表示系统输入输出的阶数,nu表示输入电压信号u(t)的采样个数。β=[β1,…,βn]T和Ck=[c1,…,cl,…,cnu]T以及cl=[cl(1),…,cl(m)]T均为系统的回归参数。
式(1)中迟滞非线性模块f[u(t-k)]通常可采用前文提到的静态迟滞模型或多项式、样条线性函数等描述。但静态迟滞模型如Presaich模型存在模型形式复杂,难以求解和不利于在线控制的特点;PI模型算子关于原点奇对称而与实际非对称迟滞曲线不符,存在原理性建模误差,模型精度有限。神经网络受限于其算法,容易陷入过学习和局部极小的情况,影响模型的泛化能力。多项式、样条函数由于形式相对简单,对迟滞现象的描述精度有限。因此,寻找合适的模型结构用以描述静态迟滞非线性有利于压电陶瓷驱动器模型精度的提高。
2 驱动器率相关Hammerstein建模
2.1 基于LS-SVM的率相关Hammerstein模型表示
支持向量机是基于统计学习理论的新型机器学习方法,同其他传统机器学习方法如神经网络相比,其关注结构经验最小化而非经验风险最小化,这使得支持向量机在小样本学习、强非线性系统等领域比传统学习方法更具优势[16]。因此可利用支持向量机对压电陶瓷驱动器静态迟滞非线性部分进行描述。
y[u(t)]=ωTφ[u(t)]+d,ω∈Z,b∈R
(2)
式中的参数ω,d待求。根据结构风险最小原理,该回归问题可转化为一个等式约束问题,其最优化目标函数如下:
(3)
满足等式约束条件:
yi=ωTφ[u(t)]+d+ei,i=1,2,…,N
(4)
目标函数(3)的第1项对应模型的泛化能力,第2项表示模型的精确性,正的常数ρ是模型泛化能力和精确性的一个折中参数,可以根据需要进行调整,ei是第i个实验数据和预测输出间的误差。
根据LS-SVM理论,Hammerstein模型中第k时刻的非线性项可表示为:
cl(k)f(ul(t-k))=cl(k)(ωTφ(ul(t-k))+d)
(5)
(6)
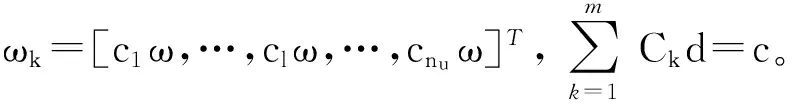
该式即为基于LS-SVM的压电陶瓷驱动器率相关迟滞Hammerstein模型。
2.2 基于LS-SVM的Hammerstein模型参数辨识
式(6)表示的最优化问题可以写成如下形式:
(7)
(8)
式中t=r,…,T,r=max(m,n)+1。
为求解方程(7)在约束条件(8)下的优化问题,使用拉格朗日乘子法构造拉格朗日函数如下:
(9)
式中αt,δk是拉格朗日乘子。由拉格朗日函数的最优值条件:
(10)
得到如下线性方程组:
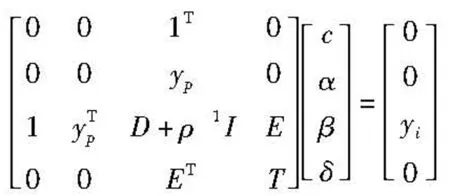
(11)
式中:
Qu(T×T)(τ,t)=φT(u(τ))φ(u(t)),t,τ=1,…,T
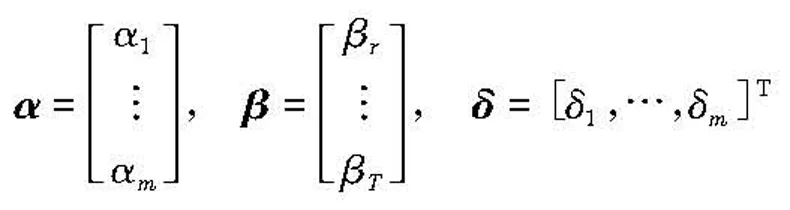
待求的参数αt,δk,βi,c可以通过求解方程组(11)得到,下面通过奇异值分解法求解回归参数Ck(k=1,…,m),构造式(12):
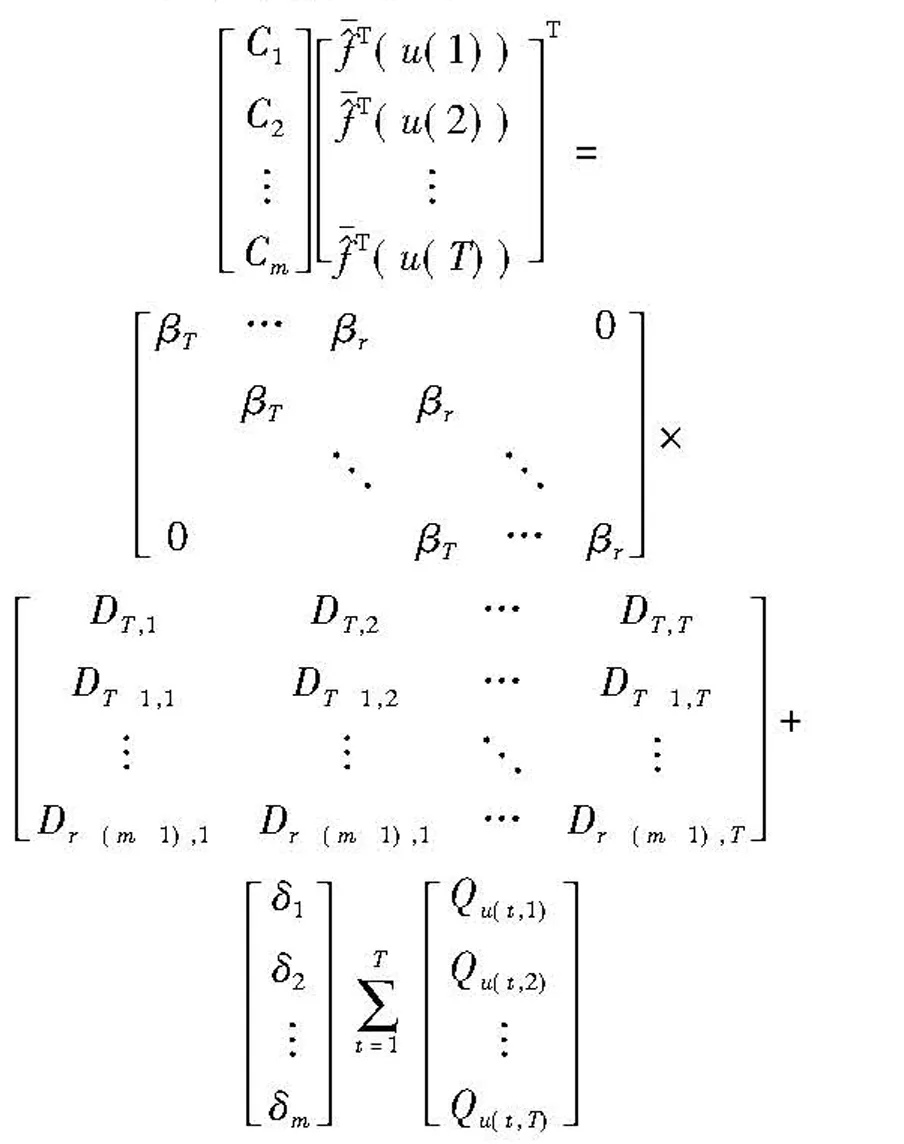
(12)
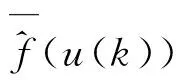
式(12)右边为已知项,因此对其进行
奇异值分解即可求得系数矩阵Ck。至此,式(1)中的参数β和Ck得以确定。
3 实验研究
为验证模型的效果,对压电陶瓷驱动器0~100 Hz输入频率下的率相关迟滞特性进行建模。实验设备如图2所示。

图2 实验仪器图
AFM是美国Veeco公司的Dimension Icon,其压电陶瓷驱动器X、Y、Z3个轴向上均能承受-220 V~+220 V的电压。实验采样频率为20 kHz,设备工作在开环模式下,取X轴向的压电陶瓷驱动器输入输出特性进行研究。
实验结果表明,输入信号频率低于1 Hz时,压电陶瓷驱动器的迟滞环几乎不发生变化,因而取1 Hz输入频率下驱动器的输入输出数据建立静态模型,该模型体现压电陶瓷驱动器的静态迟滞特性。
PI模型[17-18]是Presaich模型的一种子模型,较传统Presaich模型而言,其结构简单,运算量更小,该模型输出不随输入频率的变化而改变,属于静态模型。在输入信号频率变化时,将PI模型与率相关迟滞Hammerstein模型的输出结果进行比较,可以直观地看到率相关模型对频率变化的描述效果。
利用频率范围0~100 Hz的随机信号来激励压电陶瓷驱动器,测得其输出值并归一化。利用基于最小二乘支持向量机的参数辨识法辨识得到Hammerstein模型中的参数。模型输入输出阶数调整方法如下:先将m,n设为某固定值,然后调整ρ和σ,使用10折交叉验证法[19],使得模型在满足最小训练误差的前提下复杂度最小。得到最优ρ和σ值后,再在此基础上调节m和n,得到m和n的最优值。经验证,最终取Hammerstein模型的阶数m和n分别为3和6,模型正则化参数ρ=100,σ=0.001。
为评估所建模型的效果,定义相对均方根误差:
(13)
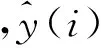
为检验模型的泛化能力,分别将10Hz、50Hz、100Hz单一频率正弦激励下率相关Hammerstein迟滞模型预测输出与实测输出进行对比,正弦信号的幅值范围均为0~140V。

图3 输入正弦信号
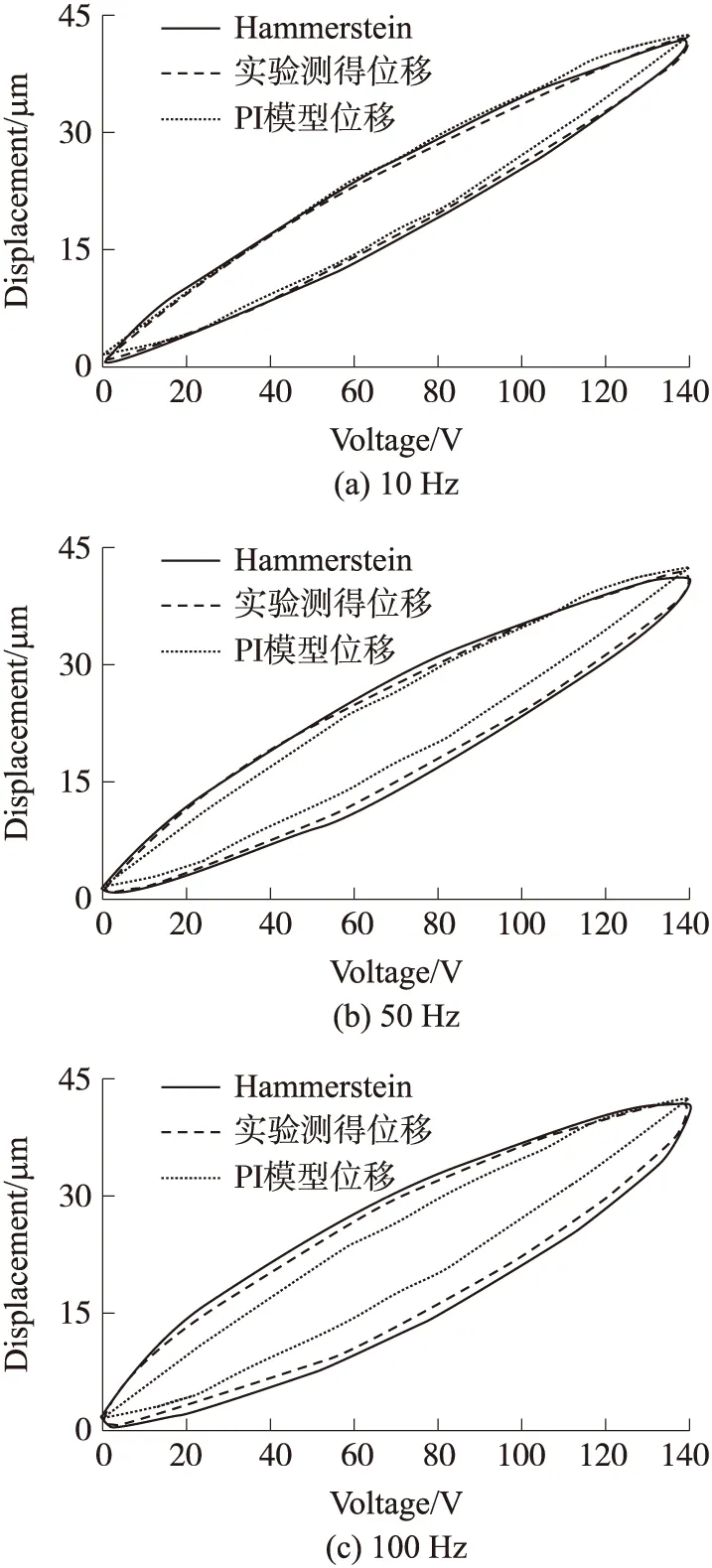
图4 Hammerstein模型检验
对比结果如图4,10Hz输入信号下Hammerstein模型的RRMSE为0.012 4,而PI模型达到了0.279 7。50Hz输入信号下,Hammerstein模型的RRMSE为0.027 7,PI模型的RRMSE为0.433 5,100Hz输入信号下,Hammerstein模型的RRMSE为0.030 1,PI模型的RRMSE为0.740 9,可见所建模型较静态迟滞模型更能体现系统的率相关迟滞动态特性,且具有良好的泛化能力。
4 结论
传统压电陶瓷驱动器静态迟滞模型无法体现系统率相关动态迟滞特性,针对这一不足,本文建立了AFM压电陶瓷驱动器率相关迟滞Hammerstein模型,在体现系统动态特性的前提下,利用支持向量机描述系统的静态线性部分。采用最小二乘支持向量机和奇异值分解法对模型中的参数进行辨识,计算量少,便于实施。实验结果表明,本文提出的模型预测准确,较传统静态迟滞模型更能反应压电陶瓷驱动器的真实特性。建模方法对此类非线性动态系统具有较高的实际应用价值。
[1]白春礼.扫描力显微术[M].北京:科学出版社,2000:3-10.
[2]纪华伟,杨世锡,吴昭同.压电陶瓷驱动器非线性建模研究[J].传感技术学报,2006,19(4):1080-1081.
[3]Ping Ge,Musa Jouaneh.Generalized Preisach Model or Hysteresis Nonlinearity of Piezoceramic Actuators[J].Precision Engineering,1997,20(2):99-100.
[4]Ru C,Sun L.Hysteresis and Creep Compensation for Piezoelectric Actuator in Open-Loop Operation[J].Sensors and Actuators A:Physical,2005,122(1):124-130.
[5]张栋,张承进,魏强.压电工作台的神经网络建模与控制[J].光学精密工程,2012,20(3):587-589.
[6]王钰锋,郭咏新,毛建琴.压电作动器的率相关迟滞建模与跟踪控制[J].光学精密工程,2014,22(3):617-619.
[7]Guo yongxin,Sun gang,Wang yufeng.Modeling and Control of Rate-Dependent Hysteresis for PEA with MPI Model-Based Hammerstein System[C]//Bao yansong.2012 International Conference on Control Engineering and Communication Technology.Shenyang:IEEE,2012:523-526.
[8]Bai E W.A Blind Approach to Hammerstein Model Identification[J].IEEE Transactions on Signal Process,2002,50(7):1610-1619.
[9]Giri F,Bai E W.Block-Oriented Nonlinear Systems IDentification[M].Germany:Lambert Academic Publishing,2010:230-240.
[10]Adam Krzyzak,Marian A Partyka.Global Identification of Nonlinear Hammerstein Systems by Recursive Kernel Approach[J].Nonlinear Analysis,Theory,Methods and Application,2005,63(5-7):1263-1272.
[11]Chen H F.Pathwise Convergence of Recursive Identification Algorithms for Hammerstein Systems[J].IEEE Transactions on Automic Control,2010,49(10):1641-1649.
[12]向微,陈宗海.基于Hammerstein模型描述的非线性系统的辨识新方法[J].控制理论与应用,2007,24(1):143-147.
[13]Pelckmans K,Goethals I,Suykens J A K,et al.On Model Complexity Control in Identification of Hammerstein Systems[C]//Eduardo F Camacho.Proceedings of the 4th IEEE Conference on Decision and Control,and the European Control Conference.Sevilla:IEEE,2005:12-15.
[14]王宏伟,韩云涛,彭继慎.基于TSPSO支持向量机红外甲烷传感器动态补偿[J].传感技术学报,2013,26(9):1193-1195.
[15]Song Haiying,Gui Weihua,Yang Chunhua.Identification of Hammerstein-Wiener Model with Least Squares Support Vector Machine[C]//Central South University.Proceedings of the 26th Chinese Control Conference,Zhangjiajie,China:IEEE,2007:260-263.
[16]乔爱民,何博侠,张炜.基于LS-SVM及嵌入式技术的力敏传感器温度补偿[J].传感技术学报,2013,26(5):638-640.
[17]Ang W T,Garmen F A,et al.Modeling Rate-Dependent Hysteresis in Piezoelectric Actuators[C]//Volker Graefe.Proceedings of the 2003 IEEE/RSJ,International Conference on Intelligent Robots and Systems.Las Vegas,USA:IEEE,2003:1976-1982.
[18]Kuhnen K.Modeling Identification,and Compensation of Complex Hysteretic Nonlinearities-Amodified Prandtl Ishlinskii Approach[J].European Journal of Control,2003,9(4):407-418.
[19]Jiang Shaohua,Gui Weihua,Yang Chunhua.Vertical Quench Furnace Hammerstein Fault Predicting ModelBased on Least Squares Support Vector Machine and Its Application[C]//Zhang Siying.Chinese Control and Decision Conference.Guilin:Northeastern University Press,2009:203-206.
Hammerstein-Based Modeling Approach and Parameter Identification Method for AFM Piezoelectric Actuator*
XUYunyang,XUKangkang,SHENPing*
(State Key Laboratory of High Performance Complex Manufacturing,Changsha 410012,China)
The piezoelectric actuator(PEA)used in the Atomic Force Microscopy(AFM)possesses a feature of rate-dependent hysteresis,which have a negative influence on the scanning and positioning accuracy of AFM.As the traditional static nonlinear hysteresis model can’t reflect the dynamic frequency characteristics of the system,a Hammerstein model here is proposed to describe the static and dynamic hysteresis characteristics of the PEA.The parameters of the model is identified by the least squares support vector machine(LS-SVM)algorithm and the singular value decomposition(SVM)method.The experiment result indicates that the rate-dependent hysteresis is well reflected,and the model accuracy is better than the traditional static hysteresis model,its application value is desirable for the analogous systems.
piezoelectric actuator;nonlinear model;Hammerstein model;system identification;support vector machine

徐运扬(1989-),男,湖南邵阳人,硕士,主要研究方向为系统建模、智能控制以及微纳米制造,xuyunyang2008@163.com;

徐康康(1990-),男,安徽淮北人,博士,主要研究方向为系统建模与温度场的管理与控制,779771244@qq.com;

沈 平(1983-),男,陕西宝鸡人,博士,主要从事复杂过程建模、自动控制、智能控制等方面的研究,dakonglong_31@163.com。
项目来源:国家重点基础研究发展计划基金项目(973)(2011CB013104)
2014-09-10 修改日期:2014-11-07
C:7320G;2860;7230
10.3969/j.issn.1004-1699.2015.01.005
TN792
A
1004-1699(2015)01-0023-05

