一种EKF-WLS-SVR与混沌时间序列分析的瓦斯动态预测新方法*

付 华,訾 海,孟祥云,孙 璐

(1.辽宁工程技术大学电气与控制工程学院,辽宁 葫芦岛 125105;2.国网辽宁省电力有限公司锦州供电公司,辽宁 锦州 121000)



一种EKF-WLS-SVR与混沌时间序列分析的瓦斯动态预测新方法*

付 华1*,訾 海1,孟祥云2,孙 璐1

(1.辽宁工程技术大学电气与控制工程学院,辽宁 葫芦岛 125105;2.国网辽宁省电力有限公司锦州供电公司,辽宁 锦州 121000)

针对瓦斯浓度时间序列高度的混沌特性,采用微熵率法同步确定最优的嵌入维数与延迟时间,还原瓦斯涌出系统状态空间。以无线传感网络系统采集并经降噪处理后的瓦斯浓度序列作为样本。提出利用带有整定因子的扩展卡尔曼滤波器(EKF)对加权最小二乘支持向量回归机(WLS-SVR)的正则化参数γ与核参数σ进行快速寻优,并依据周期性更新的训练样本建立基于EKF-WLS-SVR耦合算法的动态预测模型以精确预测后续时间点的瓦斯浓度。通过MATLAB进行仿真,结果表明:EKF滤波器对提高WLS-SVR的拟合精度与学习效率方面有很大的帮助。相比于其他模型,该耦合模型具备更高的预测精度与更强的鲁棒特性,有较高的实用价值。

动态预测;瓦斯浓度;混沌特性;无线传感网络;WLS-SVR;EKF滤波器

对回采工作面瓦斯浓度进行实时监测和准确预测是防治瓦斯突出灾害的关键也是煤矿安全生产的前提。以无线传感网络技术、数据库技术以及数据采集技术为一体的瓦斯监测系统是目前主流的综合信息处理平台。通过移动节点全覆盖井下的监测区域,能够实现对瓦斯浓度的实时监测[1]。在预测算法方面,国内外许多学者提出了支持向量机[2]、人工神经网络[3]、小波分析[4]、灰色理论[5]、D-S理论[6]等基于机器学习的预测方法。这些方法都是对瓦斯浓度短期预测的有益探索。然而,由于回采工作面地质条件的复杂性。开采期间的瓦斯涌出影响因素会发生一定程度的突变或漂移,致使井下现场采集的瓦斯浓度时间序列表现为较强的非平稳性、非线性和非高斯特性[7]。若采用单一的预测算法或固定的训练样本,预测模型的时效性不长,泛化能力上也有一定的缺陷,实用性不高。为此,本文进一步针对提高瓦斯浓度连续预测的精度及可靠性方面展开了研究。

基于结构风险最小化的加权最小二乘支持向量回归机(WLS-SVR)非常适合小样本学习且拟合精度较高[8-9]。将WLS-SVR需要优化的正则化参数γ与核参数σ作为扩展Kalman滤波器(EKF)的状态向量进而对其进行最优估计以得到全局最优参数。为加强耦合算法对瓦斯浓度混沌时间序列预测的可靠性,提出了周期更新训练样本的在线动态预测方式。通过微熵率法同步求取最优嵌入维数m与延迟时间τ以还原系统状态空间,并在重构的相空间里建立基于EKF-WLS-SVR耦合算法的预测模型来实现对回采工作面瓦斯浓度的精准预测。

1 基于无线传感网络的瓦斯监测系统

无线传感网络瓦斯监测系统由移动传感器节点、固定传感器节点以及井上信息处理中心3部分组成。其中,井下大量的移动节点依据通信空间关系或地理位置分为若干个簇并且以自组网的方式将感知的现场数据信息汇聚到簇首[10]。簇首以一个固定节点作为路由将信息通过光纤实时传输到井上信息处理中心的网关服务器。井上监控计算机处理信息后,实时显示出瓦斯浓度及井下相关数据。

图1 无线传感网络瓦斯监测系统架构

目前国内的瓦斯监测系统依然为落后的事后预警方式,即仅当瓦斯积聚超限时才报警,不具备对瓦斯浓度趋势演化的提前预测功能。因此,根据无线传感网络瓦斯监测系统采集到的信息数据,提出在井上监控计算机上建立基于EKF-WLS-SVR的瓦斯动态预测模型,以实现一种可靠、精确且具备连续非接触式预测能力的瓦斯灾害预警新方法。

2 瓦斯浓度混沌时间序列分析

由Takens定理可知,在选取合适的嵌入维数m和时间延迟τ的情况下,对一维瓦斯浓度混沌时间序列进行相空间重构就可以在更高维的空间里,通过非线性回归预测函数无奇异地拟合瓦斯涌出动力系统的演化轨迹[11-12]。

2.1 选取最优嵌入维数m与延迟时间τ

以N个样本数据与其Ns个替代数据之间的相空间微熵率最小为测度,同步考虑确定最优的嵌入维数m与延迟时间τ。避免了两个参数分开确定时造成算法上的矛盾。

(1)

ρj是第j个延迟矢量与最近邻点之间的欧氏距离;CE≈0.577 2为欧拉常数。则数据序列熵率为:

(2)

其中,n为延迟矢量个数n=N-(m-1)τ;〈·〉i是Ns个替代数据的微熵H(xs,i)的平均值算子。

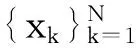
Xi=[xi-(m-1)τ,xi-(m-2)τ,…,xi]T,i=(m-1)τ+1,…,N

(3)

2.2 在线更新训练样本的动态预测策略

提出“滑动窗口”的思想,初始窗口数据序列{xj,…,xj+N-1}的长度为N。预测模型f仅以当前窗口数据序列按式(3)重构后的训练样本所建立并且仅预测当前窗口之后的W个数据点。预测完成后,窗口向前滑动W个数据点并再次建立新的预测模型f′。即模型的更新周期为W。预测模型在线更新流程如下:

①将模型f有效期间预测的W个预测点替换原窗口数据序列中前W个数据点,则滑动后的窗口数据序列为{xj+W,…,xj+W+N-1}且窗口长度保持为N;

②再次根据微熵率法确定更新后的窗口数据序列的最佳嵌入维数m′与延迟时间τ′。将重构出的N-(m′-1)τ′-1个相点作为预测模型f′的训练样本:

{⎣Xj+W+(m′-1)τ′,xj+W+1+(m′-1)τ′」,…,⎣Xj+W+N-2,xj+W+N-1」}

③利用新的训练样本确立模型f′并再次预测出后续W个数据点,窗口向前滑动。循环以上过程直至指定的预测步数。

更新后的窗口数据序列在时间上距离待测点更近。同时,对其以最优的嵌入维数与延迟时间重构出的训练样本能够保证模型与待测点间存在最大相关性。即动态更新的样本为预测模型提供了与当前瓦斯涌出非线性动力系统相匹配的先验知识。

3 WLS-SVR回归算法

WLS-SVR算法,继承了LS-SVR求解的快速性并且根据训练误差对训练样本分配权重系数vi以增强了预测函数对异常点的抗干扰能力。解决了LS-SVR鲁棒性缺失的问题。综合考虑,采用WLS-SVR算法来拟合映射函数f:Rm→R以建立预测模型。

定义样本集为{(xi,yi)|i=1,2,…,N}。WLS-SVR函数逼近问题可以归纳为如下优化问题:

其中:γ为正则化参数,ω为权矢量,δi为误差变量,b为偏差量。构造拉格朗日方程:

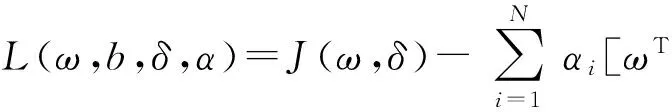
对上式各变量求偏导并消去ω,δi。可得:

(4)

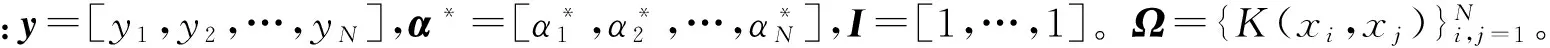
vi依据于标准LS-SVR误差变量δi=αi/γ选取

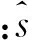
根据实际工程经验选取径向基核函数K(xi,xj)=exp(-‖xi-xj‖2/2σ2)。由式(4)求解α*与b*,确定映射函数:

(5)

4 EKF-WLS-SVR动态预测模型

正则化参数γ与核参数σ的选取直接影响WLS-SVR的预测精度。因此,需要对这两个参数进行全局寻优。常用的K折交叉验证法需要对训练样本进行反复的计算验证,耗时极大。PSO等群优化算法过度依赖初始粒子的设置,后期收敛速度慢、容易陷入局部极值。这些方法均不适合应用于预测模型的在线学习。

为此,提出将基于Kalman滤波迭代的最优估计思想引入到WLS-SVR的参数寻优上。将WLS-SVR的训练过程等效成一个非线性离散系统的动态参数估计问题。即以最小无偏差为准则,随观测序列不断对状态向量进行重估。对于非线性系统要用到扩展Kalman滤波算法(EKF)[13-14]。

4.1 引入整定因子ξ改进EKF算法

对于一般非线性离散系统

(6)

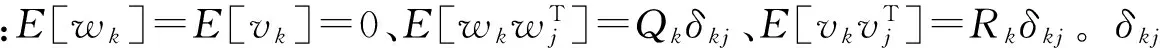
则EKF滤波器的最优估计迭代方程为:

(7)

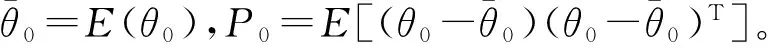
在模型的训练过程中,混沌的瓦斯浓度序列会导致观测噪声具有未知的统计特性。为快速准确跟踪样本序列的随机变化,引入一个整定因子ξ对误差方差阵进行自适应地调整。使EKF算法能够快速迭代出满足精度的最优参数。定义整定因子:

ξk=sup(1,tr[Nk-1]/tr[Mk-1])

(8)

ρ为遗忘因子且0<ρ≤1,一般取ρ=0.97。

4.2 EKF优化WLS-SVR

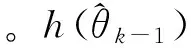
图2 基于WLS-SVR的单步预测

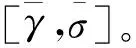
引入整定因子ξ后滤波迭代过程变为:

(9)

当样本观测值中有突变点时,残差ek会增大并直接导致残差方差阵rk的增大,由式(8)可知整定因子ξk也会相应增大。根据式(9)迭代过程,最终滤波增益Kk相应变大。因此,通过整定因子ξ使得每次迭代时为响应外界噪声的突变所产生的自适应调整作用最终落实到了对状态向量的修正上,同时避免了滤波发散。所以,改进后的EKF更适合在线训练以瓦斯混沌时间序列重构为训练样本的WLS-SVR预测模型。

EKF滤波器优化WLS-SVR步骤:

Step 1 对状态向量的误差协方差阵P0、系统噪声的方差阵Q、观测噪声方差阵R进行初始化设定;

Step 3 通过式(9)迭代方程计算当下的误差方差阵P与滤波增益K并修正由WLS-SVR的参数γ与σ组成的状态向量。

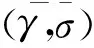
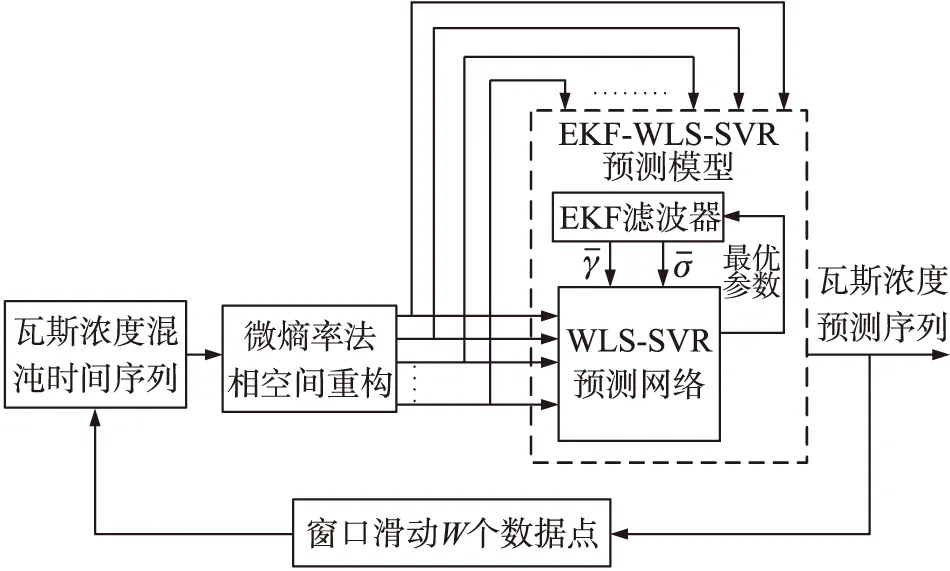
图3 EKF-WLS-SVR动态预测示意图

5 瓦斯浓度预测试验

5.1 数据预处理

试验数据来自开滦矿业集团钱营矿2074综采工作面的KJ90N煤矿安全综合监测系统。截取2013年12月份中的300个未发生瓦斯突出的瓦斯浓度实测数据和另外300个发生瓦斯突出异常时的瓦斯浓度实测数据作为研究对象。

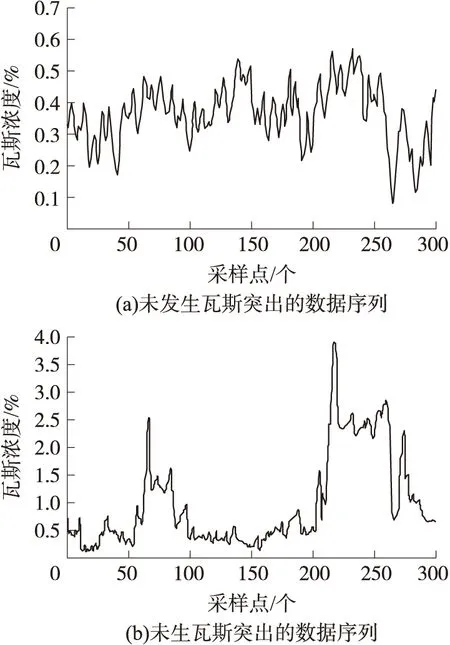
图4 去噪后的瓦斯浓度观测序列

采用sym8小波基函数对观测序列进行软阈值滤波降噪并利用文献[15]的方法计算两组数据序列的最大Lyapunov指数:λ1=0.024 795、λ2=0.085 316。均大于零,说明两组瓦斯浓度序列均具有混沌特性且λ2>λ1表明发生瓦斯突出异常时,数据序列(b)表现出的混沌行为更加明显。

5.2 预测过程

时间窗初始化,即将260个观测数据装载到时间窗口。试验选取训练样本更新周期W=20,模型f1预测前20个待测点。时间窗口滑动后建立模型f2并预测后20个待测点。利用式(2)对初始窗口数据序列求取微熵率并构出熵率图如图5所示。

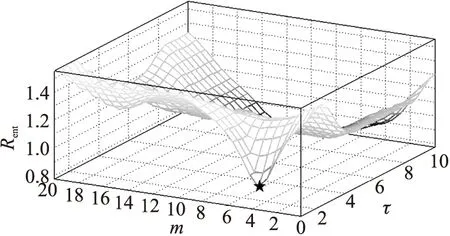
图5 瓦斯混沌时间序列熵率图

根据图5初始窗口序列的微熵率最低点“★”分别对应的m轴与τ轴的值求出m1=6,τ1=3。通过重构相空间可得到244组训练样本建立模型f1。初始化EKF滤波器参数:ρ=0.94,β=1.6,P0=50I,Q=40I,R=40I(I为2×2的单位阵);规定模型训练的允许误差范围为10-4以下。

EKF-WLS-SVR的训练收敛效果如图6所示,EKF滤波器优化WLS-SVR时迭代到350次左右便达到了训练误差精度要求,相比PSO算法寻优更快速并且收敛精度也提高了接近2个数量级。明显提高了WLS-SVR的学习效率。

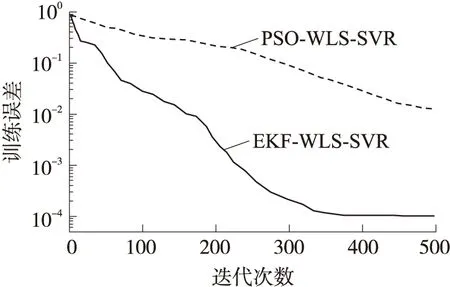
图6 EKF与PSO的收敛性对比

5.3 试验结果分析

通过MATLAB2009a进行预测算法仿真,对数据序列(a)的40个待测点的预测结果如下:

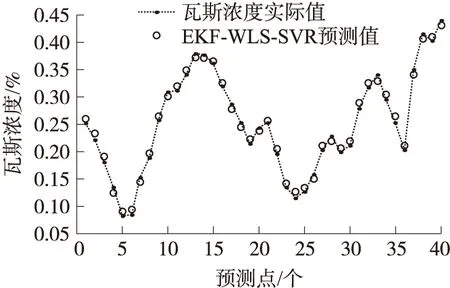
图7 数据序列(a)的瓦斯浓度预测值与实际值对比

可以看出在未发生瓦斯突出时,基于动态训练样本的EKF-WLS-SVR预测模型对于变化趋势平缓且均匀的瓦斯浓度混沌序列具有较高的预测精度和泛化能力。最大相对误差为2.17%,最小相对误差仅为0.41%,平均相对误差为1.05%。满足煤矿实际安全生产的精度需求。

图8 预测结果相对误差

发生瓦斯突出时,从数据序列(b)中可以看出此时的瓦斯浓度激增,变化幅度异常且含有较大的未知噪声。分别利用EKF-WLS-SVR与LS-SVR对序列(b)后续40点进行预测。以对比突出耦合模型对数据异常时的预测鲁棒性和可靠性。

预测结果如图9所示,EKF-WLS-SVR对于瓦斯突出时的预测平均相对误差为4.72%,依然满足实际精度要求,而LS-SVR却为15.78%。表明WLS-SVR根据训练误差以建模贡献度对样本采取的加权策略从本质上提高了模型对异常数据的鲁棒性。使得耦合算法依然能够准确跟踪大幅度随机突变情况下瓦斯浓度序列的变化规律,预测效果明显强于LS-SVR。同时引入了整定因子ξ的EKF滤波器能够在线及时获得最优参数,保证了模型的预测精度。

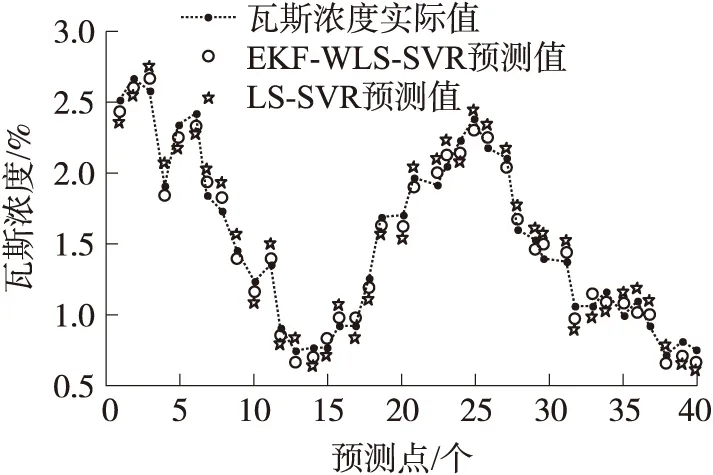
图9 数据序列(b)的瓦斯浓度预测值与实际值对比

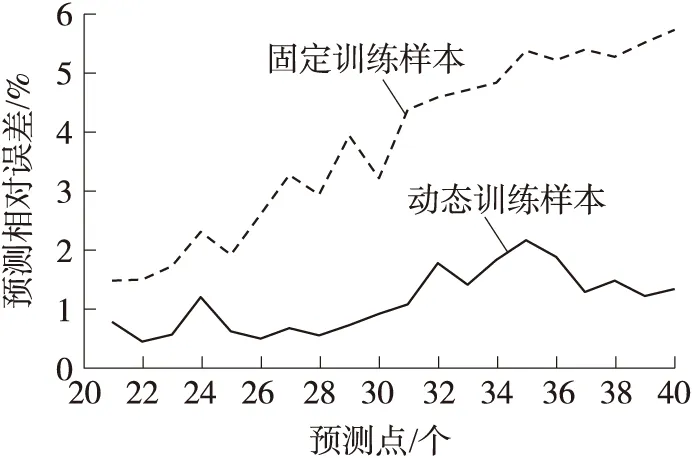
图10 动态样本与固定样本相对误差对比

为了突出动态样本的优越性,针对数据序列(a)以f1预测后20个待测点来模拟固定样本的预测模式。f1与f2对后20个待测点的预测相对误差如图10所示。

基于固定训练样本的f1在预测过程的后半段预测精度产生了明显的偏差,最大相对误差达到了5.73%,说明固定样本的模型时效性有限。在混沌时间序列初值敏感性的影响下,固定样本使得WLS-SVR回归算法无法精确拟合与较远待测点之间的映射关系。以相对均方根误差RRMSE为评判标准来评估设置不同更新周期W时模型的预测效果。其表达式为:

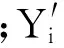
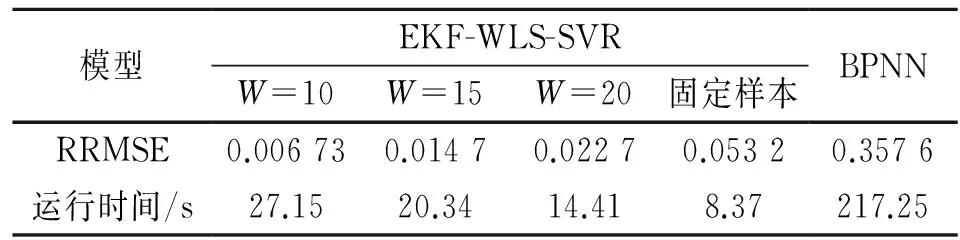
表1 预测效果对比分析

RRMSE结果显示基于动态更新训练样本的EKF-WLS-SVR预测模型的预测平均精度明显高于基于固定样本的BP神经网络预测模型。W取值越小,WLS-SVR的支持向量更新越频繁且预测模型越能表征当下的瓦斯涌出规律,使其具备更强的在线自适应能力。在运行时间方面,与EKF相结合的WLS-SVR建模所需时间短,学习效率明显提高。综合考虑预测精度要求与运行时间,该耦合模型能够实现混沌时间序列的连续精确预测。对井下瓦斯浓度的实时监测预警具有重大的实际指导意义。

6 结论

本文将基于Kalman滤波状态空间最优估计思想的EKF滤波器与WLS-SVR回归算法有机结合起来,有效提高了WLS-SVR的预测精度与学习效率。同时,提出了在线更新训练样本的动态预测策略,使得EKF-WLS-SVR耦合模型能够充分获得与当下瓦斯涌出动力系统相匹配的先验知识。保证了预测模型的时效性。利用EKF-WLS-SVR耦合算法建立的动态预测模型对井下瓦斯浓度进行试验,结果表明:该模型具有较强的鲁棒性且预测精度明显强于其他方法。能够可靠地对井下回采工作面瓦斯浓度趋势演化进行提前的精确预测。

[1]王军号,孟祥瑞.基于物联网感知的煤矿安全监测数据级融合研究[J].煤炭学报,2012,37(8):1401-1407.

[2]刘俊娥,杨晓帆,郭章林.基于FIG-SVM的煤矿瓦斯浓度预测[J].中国安全科学学报,2013,23(2):80-84.

[3]王其军,程久龙.基于免疫神经网络模型的瓦斯浓度智能预测[J].煤炭学报,2008,33(6):665-669.

[4]王晓路,刘健,卢建军.基于小波变换和优化预测器的瓦斯浓度预测[J].应用基础与工程科学学报,2011,19(3):499-508.

[5]董丁稳,李树刚,常心坦,等.瓦斯浓度区间预测的灰色聚类与高斯过程模型[J].中国安全科学学报,2011,21(5):40-45.

[6]邵良杉,付贵祥.基于数据融合理论的煤矿瓦斯动态预测技术[J].煤炭学报,2008,33(5):551-555.

[7]单亚锋,侯福营,付华,等.基于改进极端学习机的混沌时间序列瓦斯涌出量预测[J].中国安全科学学报,2012,22(12):58-63.

[8]Rubio G,Pomares H,Rojas I,et al.A Heuristic Method for Parameter Selection in LS-SVM:Application to Time Series Prediction[J].International Journal of Forecasting,2011,27(3):725-739.

[9]Hwang J P,Park S,Kim E.A New Weighted Approach to Imbalanced Data Classification Problem Via Support Vector Machine with Quadratic Cost Function[J].Expert Systems with Applications,2011,38(7):8580-8585.

[10]李纪榕,李福进,吴艳微,等.基于无线传感网络的煤矿安全监测系统设计[J].传感技术学报,2011,24(9):1336-1340.

[11]Samanta B.Prediction of Chaotic Time Series Using Computational Intelligence[J].Expert Systems with Applications,2011,38(9):11406-11411.

[12]Song J,Meng D,Wang Y.Analysis of Chaotic Behavior Based on Phase Space Reconstruction Methods[C]//Computational Intelligence and Design(ISCID),2013 Sixth International Symposium on.IEEE,2013,2:414-417.

[13]Frogerais P,Bellanger J,Senhadji L.Various Ways to Compute the Continuous-Discrete Extended Kalman Filter[J].Automatic Control,IEEE Transactions on,2012,57(4):1000-1004.

[14]徐耀松,李一博,付铜玲,等.有限空间液态场中基于优化EKF的双曲面水声定位方法研究[J].传感技术学报,2011,24(11):1579-1583.

[15]张文超,谭思超,高璞珍.基于Lyapunov指数的摇摆条件下自然循环流动不稳定性混沌预测[J].物理学报,2013,62(6):61-68.

A New Method of Mine Gas Dynamic Prediction Based on EKF-WLS-SVR and Chaotic Time Series Analysis*

FUHua1*,ZIHai1,MENGXiangyun2,SUNLu1

(1.Faculty of Electrical and Control Engineering,Liaoning Technical University,Huludao Liaoning 125105,China;2.Jinzhou Power Supply Company of Liaoning Electrical Power Company of State Grid,Jinzhou Liaoning 121000,China)

Considering highly chaotic characteristic of gas concentration time series,the differential entropy ratio method was adopted to synchronously determine optimal embedded dimension and delay time so as to restore the system state space of gas emission.The samples with noise elimination came from the gas concentration series which was collected by wireless sensor networks.Extended kalman filter algorithm(EKF)with tuning factor was proposed to rapidly optimize the regularization parameterγand the nuclear parameterσof the weighted least squares support vector regression(WLS-SVR).Periodically updated training samples were used to establish the EKF-WLS-SVR coupling algorithm-based dynamic prediction model to accurately predict gas concentration in the future.The simulation of the MATLAB shows that EKF is greatly helpful for improving WLS-SVR fitting precision and learning efficiency.The coupling model is practically useful and outperforms other prediction models in terms of prediction accuracy and robustness.

dynamic prediction;gas concentration;chaotic characteristic;wireless sensor networks;WLS-SVR;EKF

付 华(1962-),女,辽宁阜新人,教授,博士生导师,博士(后),主要研究方向为煤矿瓦斯检测、智能检测和数据融合技术。支持国家自然科学基金2项、支持及参与国家863和省部级项目30余项,发表学术论文40余篇,申请专利24项,fxfuhua@163.com;

訾 海(1989-),男,辽宁阜新人,辽宁工程技术大学电气与控制工程学院硕士研究生,主要研究方向为控制理论与控制工程,lngdzh001@163.com。

项目来源:国家自然科学基金项目(51274118);辽宁省教育厅基金项目(L2012119);辽宁省科技攻关项目(2011229011)

2014-07-08 修改日期:2014-10-09

C:7230

10.3969/j.issn.1004-1699.2015.01.022

TP391;TP212

A

1004-1699(2015)01-0126-06