钟形振子式角速率陀螺驱动控制技术研究*

李海涛,苏 中

(北京信息科技大学,高动态导航技术北京市重点实验室,北京 100101)



钟形振子式角速率陀螺驱动控制技术研究*

李海涛,苏 中*

(北京信息科技大学,高动态导航技术北京市重点实验室,北京 100101)

钟形振子式角速率陀螺采用压电激励实现驱动模态振动。利用自抗扰控制算法对钟形振子式角速率陀螺的驱动模态进行了分析,通过构建扩张状态观测器,建立了钟形振子的自抗扰驱动控制模型,设计了钟形振子式角速率陀螺驱动模态的自抗扰控制器,使陀螺工作在调谐驱动。该设计能够补偿由加工制造误差以及环境变化等引起的陀螺参数变化,实现陀螺的固定频率谐振驱动,保持陀螺驱动轴输出信号幅值恒定。结合钟形振子式角速率陀螺实际参数,通过仿真和试验对该设计进行了验证,仿真和试验结果验证了该设计的有效性和可行性。

钟形振子式角速率陀螺;驱动控制;自抗扰控制;扩张状态观测器

钟形振子式角速率陀螺,是受中国传统大钟启发而设计的一种新型哥氏振动陀螺,与传统的固体振动陀螺相比,具有更高的稳定性,能承受更高的冲击。同时具有传统固体振动陀螺所具有的精度高,能耗小,体较小,寿命长,成本低等优点,是一种新型的,极具发展潜力的惯性仪表[1-3]。

钟形振子作为钟形振子式角速率陀螺核心部件,其振动特性直接决定着钟形振子式角速率陀螺的性能。然而在实际中,不可避免的存在着材料、加工工艺等方面的缺陷和环境变化等引起的系统参数变化,最终会导致陀螺测量误差的产生,这些都将大大的降低陀螺的检测灵敏度。谐振陀螺工作的前提是谐振子以其固有频率作恒幅振动,因此,驱动回路的控制将是陀螺正常工作的前提,是振动陀螺的关键技术。在振动陀螺方面,不同机构的很多学者对振动陀螺的驱动电路进行了大量研究。振动陀螺的驱动方法主要可分为两大类:一类是基于相位控制的谐振频率跟踪方法,一类是固定频率驱动方法。文献[4]对这两种方法分别进行了相关原理介绍以及相应的误差分析。文献[5-8]研究了基于锁相环控制器和自动增益控制器的幅频控制方法在微机械陀螺、半球谐振陀螺等振动陀螺驱动控制中的应用;文献[9-12]研究了固定频率驱动技术在振动陀螺中的应用,两种方法在陀螺驱动中的应用都取得了良好的效果。

本文基于钟形振子式角速率陀螺工作原理,利用自抗扰控制算法[13]对其驱动模态进行了分析,通过扩张状态观测器的建立,设计了钟形振子式角速率陀螺自抗扰驱动回路,补偿了由加工制造误差以及环境变化等引起的陀螺参数的变化,并通过仿真和试验进行了验证。仿真和试验的结果表明该设计能够实现陀螺的固定频率和恒定幅度驱动,满足了钟形振子式角速率陀螺对驱动控制回路的要求。

1 钟形振子式角速率陀螺工作原理及动力学特性

钟形振子式角速率陀螺是基于振动质量的哥氏力效应工作的,其利用谐振子旋转产生的哥氏效应(Coriolis Effect)引起振型的移动来实现对角速度的测量[14]。钟形振子在驱动回路的驱动下,沿着驱动轴(x轴)方向以其固有频率做幅值恒定的简谐振动;当轴对称壳体绕中心轴旋转时,环向阵型不再相对于壳体静止,而要发生进动,此时,将在敏感轴(y轴)上产生哥氏加速度,通过测量敏感轴的振动可以确定其旋转角速率。钟形振子式角速率陀螺动力学模型可以用二自由度弹簧-质量-阻尼系统简单描述,如图1所示。

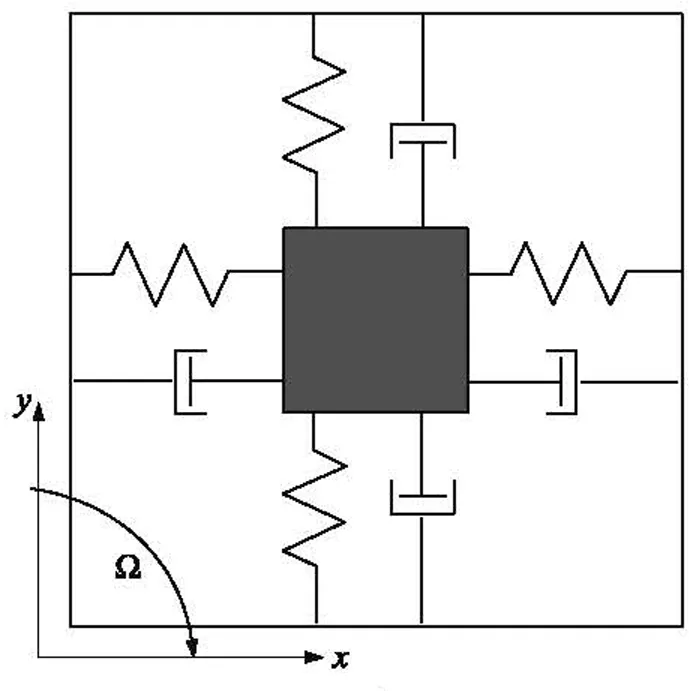
图1 二阶弹簧质量系统

忽略驱动轴与敏感轴之间的阻尼耦合,钟形振子式角速率陀螺驱动轴与敏感轴的数学模型可以用二阶耦合系统表示如下:

(1)

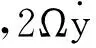
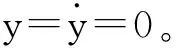
(2)

本文的控制目的是使钟形振子式角速率陀螺驱动轴工作于谐振状态,并保持恒定的振荡幅值。

2 驱动控制器设计

将钟形振子式角速率陀螺的驱动方程改写为:

(3)

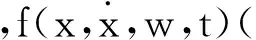
(4)

其中u0为虚拟控制信号。将式(4)代入式(3)得

(5)

则钟形振子陀螺的驱动方程可以简化为一个二阶积分器。

二阶钟形振子式角速率陀螺驱动模型的状态方程为:

(6)

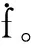
a(t)=f(x1,x2,w,t)

(7)

当作未知的被扩张的状态变量,令

x3=a(t)

(8)

那么钟形振子式角速率陀螺驱动模型的状态方程(6)变成线性系统:

(9)

基于系统方程(9),设计一个状态观测器(10)来实时估计系统状态及f。

(10)

在式(10)中,状态观测向量

g1,g2,g3是观测器增益,式(10)的状态观测器的矩阵形式为:

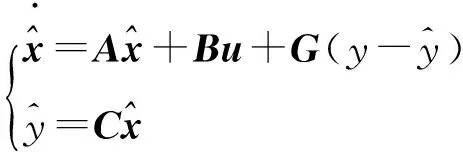
(11)

其中:

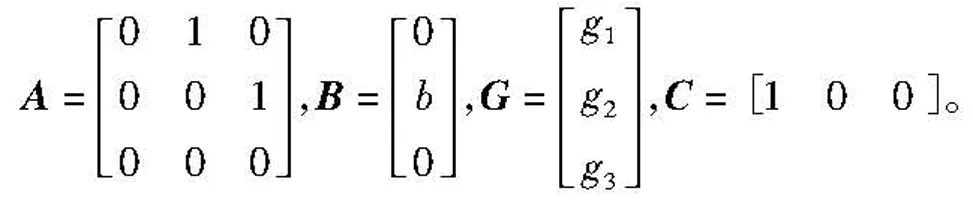
方程(11)的特征方程为:

λ(s)=|sI-(A-GC)|=s3+G1s2+G2s+G3

(12)

用极点配置法设计增益值,定义观测器带宽为ω0。根据参考文献[15]中观测器增益值的计算方法,观测器增益值取:

(13)

则方程(13)代入方程(12)得:

λ(s)=(s+ω0)3

(14)

通过设置观测器增益,该系统最终只有一个扩张状态观测器调节参数ω0。

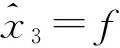
(15)

可以有效的对广义扰动f进行补偿。

假设扩张状态观测器能精确的跟踪广义扰动f,忽略观测误差,将式(15)代入式(3),原系统模型就被简化为一个二阶纯积分系统:

(16)

通过简单的比例微分控制器

(17)

即可轻易的实现控制。

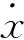
(18)

其中:

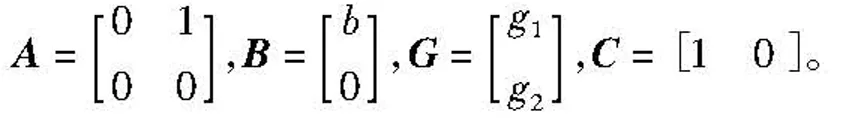
由式(18)可以看到,扩张状态观测器由三阶系统变为二阶系统。其相应的状态方程为:

(19)

λ(s)=|sI-(A-GC)|=(s+ω0)2

(20)

此时相应的控制信号及PD控制器分别为:

(21)

(22)

将式(22)代入式(21)可得

(23)

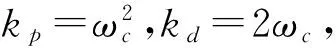
(24)

由式(19)可以求出

(25)

将式(24)(25)代入式(23)可得控制信号的方程为:

(26)

观察方程(26)右边式可知,其控制信号由不同类型滤波器组合而成,令

则方程(26)可改写为如下形式:

ud=p(r-x)+BPF(r-x)-HPF(x)+LPF(ud)

(27)

因此,驱动的设计可通过设计滤波器来实现。

3 驱动轴控制回路系统仿真

通过对钟形振子进行扫频测试,其驱动轴的谐振频率f≈6 400 Hz,其最大输出振幅A≈100 mV,品质因数Q≈1 200,因此定义参考信号r=Asin(2πf)。结合陀螺的驱动方程(2)以及控制方程(26),建立MATLAB/Simulink控制系统仿真模型,其控制原理图如图2所示。图3到图6为参考信号频率与钟形振子谐振频率一致时(fr=fx=6 400 Hz)的仿真结果图。

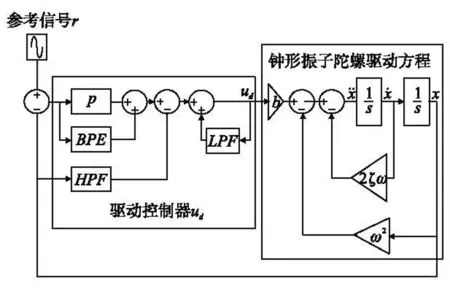
图2 BVG驱动控制原理图

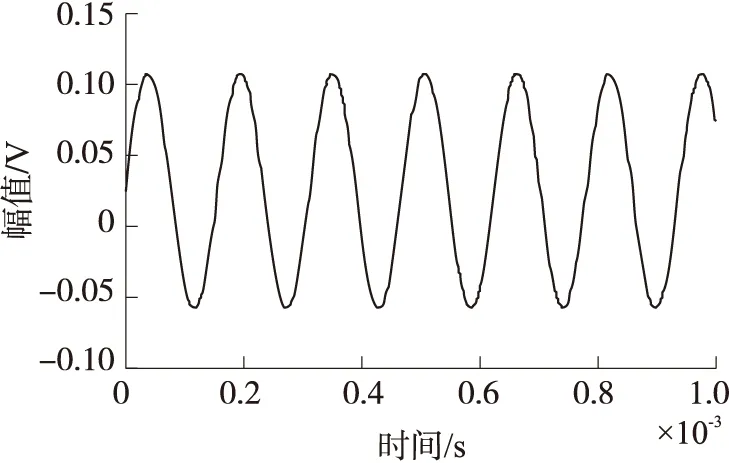
图3 驱动轴参考信号(r)

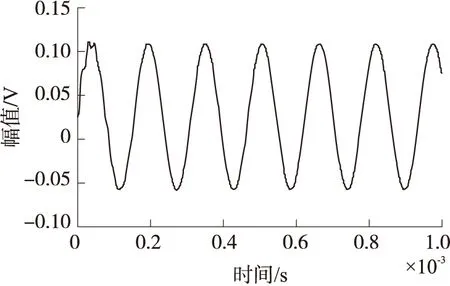
图4 驱动轴位移输出信号

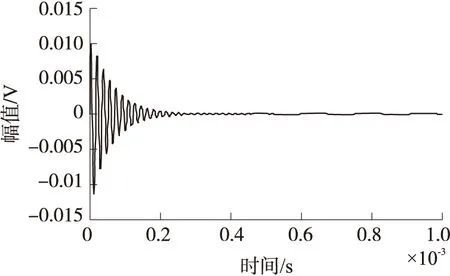
图5 驱动控制误差信号e

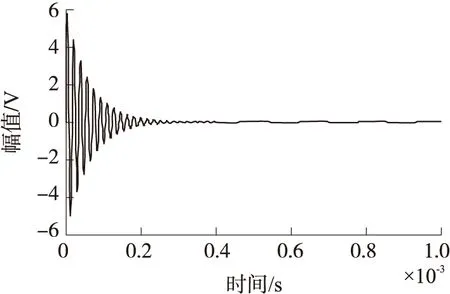
图6 驱动轴控制信号

对比图3和图4可知,驱动轴的输出信号能很好的跟踪参考信号,过渡过程快,大约60 μs,在过渡过程中,最大超调量约为3.1%,在动态过渡完成后,驱动轴的幅值和频率都保持在一个恒值。由图5和图6可知,在系统工作的初始时刻,误差信号e(参考信号r与驱动轴输出信号x的差值)与控制所需的控制信号ud均较大,随着时间的推移,误差信号e与控制信号ud成指数衰减,当系统进入稳态后,误差信号e与控制信号ud收敛于一个很小的范围内。

保持参考信号幅值与频率不变,改变钟形振子的谐振频率,对不同谐振频率钟形振子的仿真结果如表1所示。

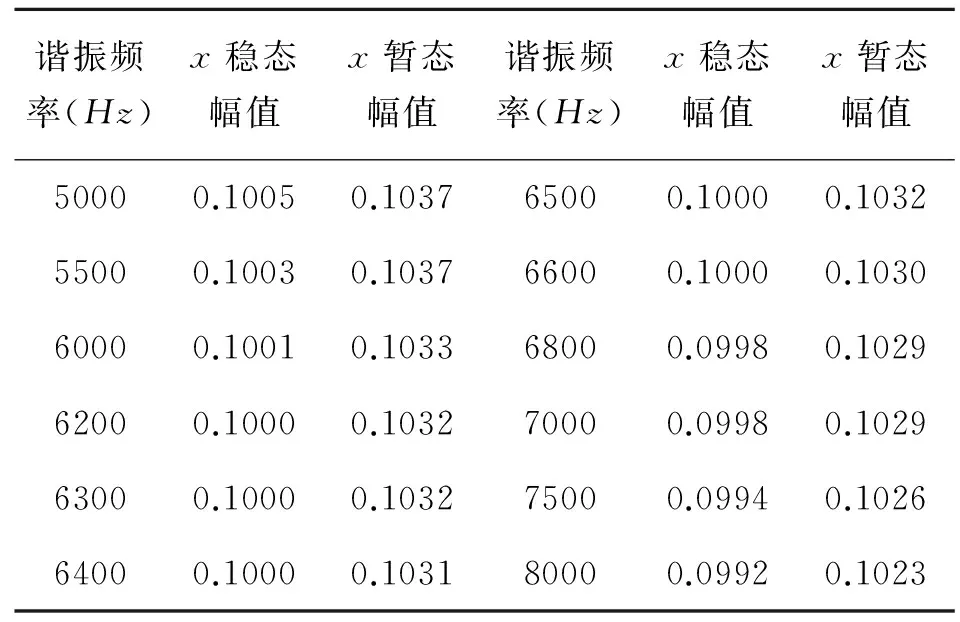
表1 不同谐振频率下固定频率驱动仿真结果

由表1中可以看出,当钟形振子谐振频率偏离原谐振频率1000 Hz以上时,驱动轴的稳态输出仍能很好的跟踪参考信号,证明了自抗扰控制器的有效性,通过自抗扰控制可以有效的对进入系统的各种扰动进行补偿,满足了陀螺对驱动轴的控制要求。

4 试验结果

自抗扰控制算法可以通过模拟或者数字方式实现,本文中采用模拟方法实现。模拟方法实现速度快,成本低。根据方程(27),用滤波电路的组合来实现自抗扰控制器,各环节的电路设计原理图如图7所示,试验电路板照片如图8所示。图9为陀螺的实际试验图,其中上方曲线为驱动轴参考信号,下方曲线为驱动轴实际输出位移信号,通过对比驱动轴参考信号与驱动轴实际输出信号波形图发现,驱动轴参考信号比较光滑,而驱动轴输出信号由于被元器件噪声污染以及少量谐波的出现导致出现毛刺,从而导致驱动轴实际输出信号幅值稍稍大于驱动参考信号幅值。从试验测试结果可以看出,陀螺驱动轴的输出能够很好的跟踪参考信号,并与参考信号基本保持一致,满足陀螺对驱动轴的性能要求。

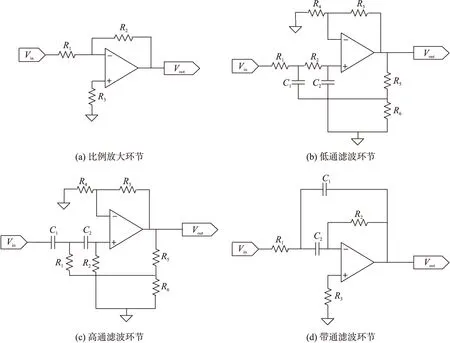
图7 自抗扰控制器各环节电路设计原理图

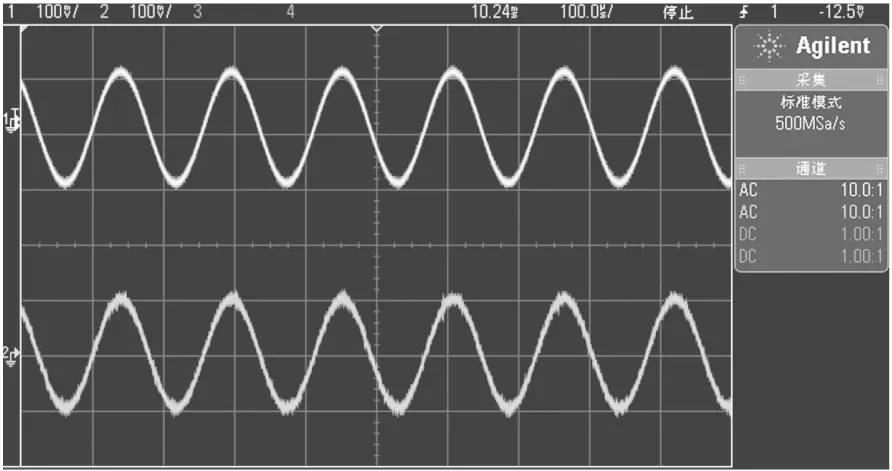
图9 驱动轴参考信号与驱动轴输出信号

图8 试验电路板照片

5 结论

本文针对钟形振子制造加工误差以及环境变化给系统带来的各种扰动,通过建立扩张状态观测器,对扰动进行精确估计,设计了基于自抗扰控制算法的钟形振子式角速率陀螺驱动回路。通过仿真和试验对该设计进行了验证,结果证明了该设计的有效性和可行性,为钟形振子式角速率陀螺其他控制回路的设计打下了基础。

[1]刘宁,苏中,刘洪.钟形振子式角速率陀螺敏感机理与检测方法[J].哈尔滨工程大学学报,2013,34(6):721-727.

[2]Su Zhong,Fu Mengyin,Li Qing,et al.Research on Bell-Shaped Vibratory Angular Rate Gyroscopes Character of Resonator[J].Sensors 2013,13:4724-4741.

[3]季林,苏中,宋艳敏,等.钟形陀螺微纳振幅曲面电容检测方法研究[J].传感技术学报,2013,26(6):825-829.

[4]Sungsu Park,Chin-Woo Tan,Haedong Kim,et al.Oscillation Control Algorithms for Resonant Sensors with Applications to Vibratory Gyroscopes[J].Sensors,2009(9):5952-5967.

[5]罗兵,王安成,吴美平.基于相位控制的硅微机械陀螺驱动控制技术[J].自动化学报,2012,38(2):206-212.

[6]李芊,李晓莹,常洪龙,等.振动式微机械陀螺驱动控制技术电路研究[J].传感技术学报,2006,19(5):2230-2232.

[7]Wang Xu,Wu Wenqi,Luo Bing,et al.Force to Rebalance Control of HRG and Suppression of Its Error on the Basis of FPGA[J].Sensors,2011(11):11761-11773.

[8]Sun X,Horowitz R,Komvopoulos K.Stability and Resolution Analysis of a Phase-Locked Loop Natural Frequency Tracking System for MEMS Fatigue Testing[J].Journal of Dynamic Systems,Measurement and Control,2002,124(4):99-605.

[9]王存超,王寿荣,周百令.基于随机平均法的MEMS陀螺自适应控制设计[J].仪器仪表学报,2008,29(4):841-844.

[10]Leland R P.Adaptive Mode Tuning for Vibrational Gyroscopes[J].Transactions on Control Systems Technology,2003,11(2):242-247.

[11]Zhu Huijie,Jin Zhonghe,Hu Shichang,et al.Constant-Frequency Oscillation Control for Vibratory Micro-Machined Gyroscopes[J].Sensors and Actuators A;Physical,2013:193-200.

[12]Lili Dong,David Avanesian.Drive-Mode Control for Vibrational MEMS Gyroscopes[J].IEEE Transactions on Industrial Electronics,2009,56(4):956-963.

[13]韩京清.自抗扰控制技术[J].前沿科学,2007(1):24-31.

[14]Spiess H,Lau B.Analysis of Bell Vibrations[J].Acustica,2008,78(2):46-54.

[15]董莉莉.自抗扰控制技术在微机电换能器中的应用[J].控制理论与应用,2013,30(12):1543-1552.

[16]刘豹,唐万生.现代控制理论[M].机械工业出版社,2008:216-220.

[17]Gao Z.Scaling and Bandwidth-Parameterization Based Controller Tuning[C]//Proceedings of the 2003 American Control Conference.Denver,Co:IEEE,2003:4389-4996.

Research on Drive Control of Bell-Shaped Vibratory Angular Rate Gyro*

LIHaitao,SUZhong*

(Beijing Key Laboratory of High Dynamic Navigation Technology,Beijing Information Science and Technological University,Beijing 100101,China)

Bell-shaped vibratory angular rate gyro(abbreviate as BVG)use piezoelectric excitation to achieve drive-mode vibration.This paper presents an active disturbance rejection control(ADRC)design for the drive control of BVG to makes the BVG work on tune driven,which is based on the analysis of drive mode using ADRC algorithm and the established of ADRC model by construct an extended state observer(ESO).This design can tunes the resonant frequency of the resonator to the specified resonant frequency by altering the resonator dynamics and maintain the specified amplitude of the oscillation through effectively compensating the imperfections in fabrications and environmental variations.The design was verified by simulation and experiment combined with practical parameters of gyro,and simulation and experimental results demonstrate the effectiveness and feasibility of this design for BVG.

BVG;drive-mode control;ADRC;ESO

李海涛(1984-),男,汉族,在读研究生,籍贯山东。2006～2010年,在北京信息科技大学读本科,专业为自动化;2012至今,在北京信息科技大学读研究生,控制工程专业,主要从事惯性器件和高动态IMU研究,lihaitao99@gmail.com;

苏 中(1962-),男,汉族,教授,博士生导师,籍贯安徽。1979～1983年北京工业学院自动化专业本科;1986～1989年北京理工大学计算机控制硕士学位研究生;1994～1998年北京真空电子技术研究所博士学位研究生。主要从事惯性器件、高动态IMU和组合导航的研究,suzhong2011@126.com。

项目来源:国家自然科学基金重点项目(61031001);十二五预先研究项目(40405100304,9071223301)

2014-07-22 修改日期:2014-11-13

C:1205;1220;7230M;7320Z

10.3969/j.issn.1004-1699.2015.01.006

TN384

A

1004-1699(2015)01-0028-06