纵弯转换超声振动雾化系统的振动特性与设计研究

李 华, 任 坤, 殷 振, 赵江江, 曹自洋, 吕自强

(1.苏州科技学院机械工程学院， 江苏 苏州 215009；2.河南工业大学机电工程学院， 河南 郑州 450007)

纵弯转换超声振动雾化系统的振动特性与设计研究

李 华1, 任 坤2, 殷 振1, 赵江江2, 曹自洋1, 吕自强2

(1.苏州科技学院机械工程学院， 江苏 苏州 215009；2.河南工业大学机电工程学院， 河南 郑州 450007)

提出了由纵向振动系统与弯曲振动圆盘组成的纵弯转换超声振动雾化系统的新型结构。通过理论分析和有限元分析，揭示了由换能器、变幅杆与工具组成的振动系统的各种谐振状态特性, 研究了系统的谐振设计方法。分析表明：新型雾化振动系统工作于负载谐振模式，其谐振频率主要取决于纵振动系统的结构，弯曲振动薄圆盘相当于系统的负载。当弯曲振动圆盘谐振频率与系统的谐振频率越接近时，系统的输出振幅越大。通过实验证明了理论研究正确性。

超声; 振动;雾化; 纵弯转换

引 言

在切削磨削加工过程中，温度是影响加工质量和加工效率的重要因素。实现微量、高效和绿色的冷却，保证磨削质量，是先进磨削技术研究的热点之一[1]。传统的浇注冷却方式存在冷却效率低、污染环境等问题；而高压喷雾冷却存在着系统复杂、环保效果不佳、噪声大等不足[2]。超声振动辅助气雾冷却技术是利用超声振动雾化技术使切削液雾化，并加注到切削区，从而实现加工过程冷却的一项新技术。它可以提高冷却效果，大大减少冷却液的用量，实现准绿色加工。雾化振动系统是超声振动气雾冷却系统实现雾化冷却作用的关键部件。目前采用的雾化振动系统大致可分为两类:一类是利用夹心式纵向振动换能器的纵向振动实现雾化，冷却液在变幅杆端面超声振动的作用下实现雾化[3～5]，这种方式可以实现大功率的驱动，但由于结构限制，难以实现高频振动，雾化的气雾颗粒较大；另一类是利用圆盘的弯曲振动或厚度振动模式实现雾化，如超声加湿器的雾化系统。这种方法可以实现高频振动，气雾的颗粒小，但难以实现大功率的驱动，气雾形成后多以自由状态漂浮。

在切削、磨削加工中，需要流量足够、颗粒小、并且有一定的速度和确定方向的气雾作用到切削区来实现冷却效果。基于这一要求，提出了采用纵弯转换模式的新型超声雾化振动系统结构[6]，研究表明，这一结构综合了夹心式纵向振动雾化器和圆盘弯曲振动雾化器的优点，可以实现大功率输出和高频振动，能够满足加工过程气雾冷却的需要。本文主要研究这一结构的谐振特性和设计方法。

1 振动雾化系统的结构和谐振状态的理论分析

1.1 新型雾化系统结构

图1(a)是本文研究的新型超声振动雾化系统的结构示意。在电源驱动下压电陶瓷换能器和阶梯型变幅杆产生超声振动，冷却液从换能器的末端输入，经过中心的通道到达变幅杆的端部，在变幅杆振动的驱动下产生雾化。在变幅杆端部，杯形雾化圆盘3与纵向振子2的端部以螺纹连接，成为一个整体(图1(b)所示)。在变幅杆的纵向振动驱动下，圆盘产生轴对称弯曲振动。冷却液从供液管道1输送到振子的前端，在圆盘的端面雾化。

图1 超声振动雾化系统Fig.1 The ultrasonic vibration mist system

当夹心式压电换能器、变幅杆和圆盘连接良好时，整个复合振动系统(以下简称复合系统)可以看作是由一个纵振动系统(包含换能器与变幅杆)与一个弯曲振动薄圆盘(简称圆盘)组成，圆盘的周边与纵振动系统端部的周边固联。当纵振动系统在电源驱动下做纵向振动时，带动其端部的圆盘做轴对称弯曲振动。

1.2 复合系统的等效阻抗

为分析方便，把压电换能器简化为一段当量等截面杆，与阶梯变幅杆一起组成纵振动系统，这一系统再与弯曲振动圆盘组成复合系统,其简化模型如图2所示。

图2 纵弯转换振动系统简化模型Fig.2 The simplified model of the longitudinal-flexural vibration conversion system

由振动理论可知，纵振动杆沿轴向(x向)的纵振动位移y(x)为

y(x)=Acoskx+Bsinkx

(1)

由板壳振动理论[10]可知，弯曲振动圆盘的轴对称弯曲振动振型W(r) 为

W(r)=AnJ0(knr)+BnI0(knr)

(2)

根据超声振动系统的四端网络理论[7]，图2的系统模型可用图3等效阻抗网络来表示。

图3 纵弯复合振动系统的等效电路Fig.3 The equivalent circuit of the composite vibration system

其中， 设zi=ρicisi为纵振动系统各段材料的特性声阻抗；li为各段的长度。i=0，1，2分别代换能器部分、变幅杆大端、变幅杆小端。Xn、Mn和Kn分别是弯曲振动圆盘的等效阻抗、等效质量和等效刚度。

由图3的等效网络，推导可得，复合系统的等效输入阻抗为

(3)

1.3 弯曲振动雾化圆盘的等效阻抗

圆盘周边固定时，其边界条件为：在外圆边界处(r=r0)弯曲振动位移和转角为零，由式(2)和贝塞尔函数性质可得：

(4)

(5)

由式(4),(5)可得周边固定圆盘的频率方程

J0(knr0)I1(knr0)+J1(knr0)I0(knr0)=0

(6)

以圆盘的中心(r=0)为参考点时，圆盘振动的动能可表示为[8]

(7)

又根据动能的定义可得，圆盘振动的总动能为：

(8)

(9)

同理，以圆盘中心为参考点时圆盘的势能可表示为

(10)

根据薄板弯曲的势能密度定义，可以推得圆盘弯曲振动时的总势能为

(11)

由Es=E′s，根据式(10),(11)和(5)推导可得

-2knr0J1(knr0)I1(knr0)[J0(knr0)I1(knr0)+

(12)

由式(9)，(12)可得

(13)

显然，圆盘谐振时，有Xn=j(ωMn-Kn/ω)=0，同样可得频率方程式(6)。

2 复合系统的振动特性分析

由式(3)可知，当系统处于谐振状态时，有Z=0，即有：

A+jBX=0

(14)

为系统的谐振频率方程。

(1)当X=0时，圆盘处于谐振状态。复合系统完全谐振的条件是A=0，这就是纵振动系统的谐振频率方程。这时复合系统的每一部分都处于谐振状态。由A=0可得

(15)

为纵振动系统的谐振频率方程。把式(6)和(15)联立设计圆盘和纵振动系统，就可使系统处于谐振状态。这种谐振状态称之为完全谐振状态。在完全谐振状态下，复合系统从理论上讲是处于最佳振动状态，输出效率最高。但是由于其中各子系统都存在机械阻尼，而且各子系统的机械连接部位都不可避免地存在接触阻抗，所以随着子系统数量的增加，复合系统的机械品质因数会减小，实际输出效率会降低。

(2)当X≠0时，如果式(14)成立，则有A≠0。在忽略机械阻尼的前提下，这时整个复合系统处于阻抗为零的谐振状态，但其中的纵振动部分和圆盘并不处于各自的谐振状态，本文称这种状态为不完全谐振状态。

在功率超声应用中，振动系统大多由纵振动系统与末端的工具共同组成复合系统，根据纵振动系统与工具之间的耦合状态不同以及两者特性阻抗的大小不同，不完全谐振有如下3种振动模式：

1) 整体谐振模式

当纵振动系统和工具相互之间的耦合状态良好，而且特性阻抗在差别不大时，两者在耦合面处的运动学、动力学和受力边界条件连续。整个复合系统表现为一个连续系统，其谐振频率与各子系统的谐振频率无关，这一状态在笔者以往的研究中已有论述[9]。在实际应用中，大多数复合系统都是处于这种谐振模式。这时系统中各部分之间的耦合面会影响系统的谐振阻抗。

2) 负载谐振模式

负载谐振模式是系统整体谐振的一种特殊情况，其谐振频率取决于纵振动系统的谐振频率，输出振幅受纵振动系统结构、工具质量和谐振频率的影响。质量负载越小，输出的振幅越大；工具自身谐振频率与纵振动系统的谐振频率越接近，输出振幅也越大。

3) 局部共振模式

当纵振动系统与工具之间在耦合连接处的截面积差距很大时，两者的连接处于一种弱耦合状态，力学连续性条件不完全成立，两者之间不能作为一个连续的整体系统，而相当于两个独立系统的弱耦合。当两者的谐振频率相差不太大时，工具的激励可以来自于耦合连接处纵振动系统施加的驱动力。当电源的激励频率为工具的谐振频率时，虽然纵振动系统不处于谐振状态，但工具部分处于谐振状态，工具受到耦合处纵振动系统的微小振动激励而产生谐振。系统的谐振频率取决于工具的谐振频率。这就是国内许多学者所称的“局部共振”现象[10]。功率超声的应用研究证明了这种状态存在。在“局部共振”模式下，由于变幅杆的输出端的振幅很小，所以工具与纵振动系统的连接处振幅很小，工具的振动近似呈现出一端固定的振动结构的谐振振型。

3 系统谐振状态的有限元分析

本文研究的结构中，相对于纵振动系统而言圆盘很小，在大多数情况下复合系统处于负载谐振模式。给定圆盘的结构参数，通过改变变幅杆前端长度来改变纵振动系统的参数。圆盘相当于与不同结构的纵振动系统组成复合系统，这一系统多处于不完全谐振状态。由式(14)应用Matlab软件计算就可以求出不同结构参数下复合系统的谐振频率，由式(6)可以求出圆盘的弯曲振动谐振频率。同时，应用有限元分析软件可以求出不同结构参数下的复合系统谐振频率。通过把理论计算结果与有限元分析结果对比，来分析系统的谐振特性。

为分析方便，设纵振动系统由等截面换能器与阶梯变幅杆构成。取圆盘厚度h=0.5 mm，半径r0=6 mm，材料为不锈钢；换能器后端盖长度l1为13和28 mm，直径20 mm，材料为45钢，PZT8压电陶瓷片(2片)厚度为6 mm；变幅杆材料为不锈钢，前端直径为14 mm。

3.1 谐振频率

图5是前端杆长度变化时，复合系统前2阶纵振模式谐振频率和1阶弯曲振动模式谐振频率。图中fzf,fwf是有限元计算曲线，fz,fw是理论计算曲线。图6是纵振动系统和雾化圆盘的谐振频率，图中ftf,fpf分别为纵振动系统和圆盘谐振频率的有限元计算结果。ft,fp分别为纵振动系统和圆盘谐振频率的理论计算结果。

图4 系统谐振的有限元分析Fig.4 The FEM analysis of the vibration system resonance

图5 复合系统谐振频率Fig.5 The resonance frequency of the composite system

图6 圆盘与纵振动系统谐振频率比较Fig.6 The comparison of the disc and the longitudinal vibration system

由图5和6的结果可以看出：理论分析和有限元分析的结果相接近，证明了理论分析的正确性。对于一定的系统结构，理论上复合系统有两种谐振模式，一种是纵振动谐振模式，其谐振频率与纵振动系统的谐振频率fz相近，纵振动系统带动端部的圆盘振动，这就是负载谐振模式；另一种是圆盘弯曲振动谐振模式，其谐振频率与圆盘的弯曲振动谐振频率fw相近，这时纵振动系统振动很小或完全不振动，只有圆盘振动，系统处于局部共振模式。在局部共振时，如果纵振动系统与弯曲振动圆盘的谐振频率相差较大时，纵振动系统的振动等效阻抗很大，当电源的输出阻抗与系统的输入阻抗不匹配时，纵振动系统不能产生振动，弯曲振动圆盘得不到振动的激励，也就无法在该频率点振动。所以在实际系统中只存在负载谐振模式。

3.2 谐振幅值

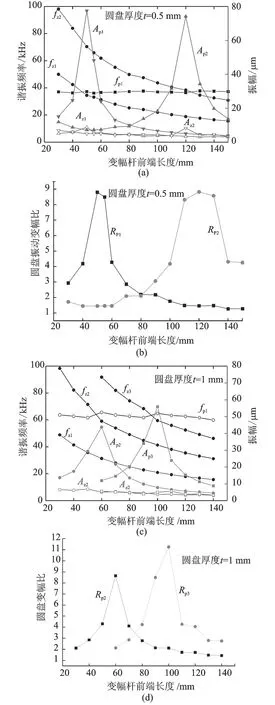
图7 系统的谐振幅值分析Fig.7 The analysis of the resonance amplitude of the composite system

图7所示为不同结构纵振动系统和弯曲振动圆盘构成的复合系统谐振输出振幅和圆盘变幅比的有限元分析结果，图中fz1，fz2，fz3，fP1分别为复合系统的1，2，3阶纵振谐振频率和一阶弯曲谐振频率；Az1，Az2，Az3和Ap1，Ap2，Ap3分别为在1，2，3阶纵振谐振频率下变幅杆端部和圆盘中心点振幅，Rp1，Rp2，Rp3分别是圆盘中心与变幅杆端部的变幅比。

由结果可以看出：当纵振动谐振频率与弯曲振动谐振频率相等时，复合系统处于完全谐振状态，圆盘有最大的振幅输出，除此以外系统都处于负载谐振模式。对于一定的结构，纵振动系统有多阶谐振频率，当圆盘的谐振频率某一阶纵振动谐振频率接近或相等时(图中fz与fP的交叉点)，由于弯曲振动圆盘具有的变幅作用，复合系统就可以有较大的振幅输出。反之，输出振幅趋近于纵振动系统的振幅。

由图7(a)和7(c)可以看出，当t=0.5 mm时，在纵振动的1，2阶谐振频率与弯曲振动的频率交叉点附近，复合系统的谐振频率在35 kHz附近；当t=1 mm时，在纵振动的2、3阶谐振频率与弯曲振动的频率交叉点附近，复合系统的谐振频率在63 kHz附近。都有大的振幅输出。所以通过改变圆盘的结构参数就可以实现高频率和大振幅的输出。

4 实验研究

根据理论分析结果，设计了多种不同结构的超声振动雾化振动系统并进行测试，图8是其中两种结构的新型雾化系统，图8(a)是用简单的阶梯型铝合金变幅杆构成的换能器(以下称为A结构)，图8(b)在变幅杆的前端杆部分采用了钛合金阶梯杆结构以实现阻抗的变换(以下称为B结构)。其端部与杯型雾化圆盘连接的结构相同。

图8 两种纵弯转换超声雾化系统的结构Fig.8 The structure of two types of ultrasonic mist system

针对上述两种结构，分别用阻抗分析仪测试换能器和组合系统的谐振频率。并应用光纤测振仪测量雾化圆盘的振幅。实验系统如图9所示。其中，A结构的雾化圆盘外直径为14 mm，B结构的雾化圆盘外直径为12 mm, 内径均为10 mm, 厚度为0.5 mm。 针对A结构，分别采用0.3，0.5,0.7 mm三种厚度的圆盘，组成振动系统，测试系统的谐振频率、阻抗和圆盘端面振幅及雾化效果。实验测试结果见表1和2。

图9 雾化系统测试实验系统Fig.9 The test scheme of the mist system

结果表明，复合系统的谐振频率FZ与纵振动系统谐振频率接近，系统工作在负载谐振模式，圆盘厚度变化对系统的谐振频率影响很小。有限元分析得到t=0.5 mm时圆盘的谐振频率为31.2 kHz, 与A结构中fz1最接近，所以系统谐振阻抗最小，振幅最大。B结构的变幅杆采用了钛合金材料，声学性能好于A结构中的铝合金，所以虽然频率差距增大，但阻抗和振动效果变化不大。图10为雾化效果的试验照片。

表2为圆盘厚度变化时，系统的一阶纵振频率和振幅变化测试结果。可以看出：圆盘的厚度改变时，影响其弯曲振动谐振频率，但是在负载谐振模式下，当纵振动系统结构一定时圆盘厚度变化对系统的谐振频率影响很小。圆盘的谐振频率与系统的谐振频率越接近，系统的输出振幅就越大。

表1 不同结构系统谐振特性的实验结果

Tab.1 The test results of the system resonance properties with different structu

系统结构A结构B结构阻抗分析结果纵振动系统谐振频率/kHzfz124．0fz255．6fz256．6fz367．8复合系统频率/kHz23．454．854．667．5复合系统阻抗/Ω46216197222实测结果复合系统频率/kHz23．654．354．365．7圆盘中心振幅/μm2919．82024雾化效果 好好好好

表2 圆盘对系统谐振的影响实验结果

Tab.2 The test results of the influence of disc to the resonance of system

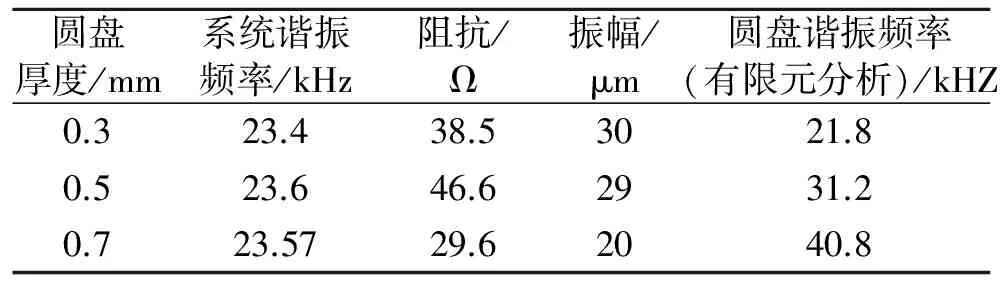
圆盘厚度/mm系统谐振频率/kHz阻抗/Ω振幅/μm圆盘谐振频率(有限元分析)/kHZ0．323．438．53021．80．523．646．62931．20．723．5729．62040．8

图10 新型雾化系统的雾化效果Fig.10 The mist experiment result of the new system

5 结 论

由纵向振动系统与雾化圆盘可以组成纵弯转换超声振动雾化系统。由于雾化圆盘结构较小，在大多数情况下，这一组合系统工作在负载谐振模式，谐振频率取决于纵振动系统。应用纵振动的谐振频率计算方法可以方便地计算系统的谐振频率，实现系统的设计。在负载谐振模式下，系统的输出振幅受圆盘谐振频率影响，利用圆盘弯曲振动的特性，系统的振幅可以实现二次放大。两者谐振频率越接近，系统的输出振幅就越大。通过设计高频率的雾化圆盘，使之与纵振动系统的某一阶谐振频率相一致，就可以发挥纵振动系统的大功率输出优势和弯曲振动的高频及变幅优势，实现高频大功率的超声振动雾化系统，取得更好的雾化效果。

[1] Tawakoli T, Hadad M J, Sadeghi M H, et al. An experimental investigation of the effects of workpiece and grinding parameters on minimum quantity lubrication-MQL grinding[J]. International Journal of Machine Tools & Manufacture, 2009, 49:924—932.

[2] 袁巨龙，王志伟，文东辉，等. 超精密加工现状综述[J]. 机械工程学报，2007,43(1)：35—48.

YUAN Julong, WANG Zhiwei, WEN Donghui, et al. Review of the current situation of ultra-precision machining[J]. Chinese Journal of Mechanical Engineering, 2007,43(1)：35—48.

[3] 黄卫星，高建民，陈翠英.超声雾化的研究现状及在农业工程中的应用[J]. 农机化研究，2007，3：154—158.

HUANG Weixing，GAO Jianmin, CHEN Cuiying. Present situations and prospects of ultrasonic atomization application[J]. Journal of Agricultural Mechanization Research,2007,3: 154—158.

[4] YI Hong, HUANG Jie, GU XingZhong,et al. Study on ultrasonic spray technology for the coating of vascular stent[J]. SCIENCE CHINA Technological Sciences, 2011, 54 (12): 3 358—3 370.

[5] Vladimir N Khmelev, Andrey V halunov, Maxim Vkhmee V, et al. Ultrasonic Atomizer of Nanomaterials[J]. XII International Conference and Seminar EDM’2011, ERLAGOL, section VIII,305—309.

[6] 李华，任坤，殷振，等. 纵弯转换超声振动球面聚焦系统聚焦特性研究[J]. 压电与声光，2014，36(3):450—454.

LI Hua, REN Kun, YIN Zhen, et al. Study on sonic focusing properties of ultrasonic vibration spherical focusing system based on longitudinal-bending vibration conversion[J]. Piezoelectrics & Acoustooptics,2014, 36(3):450—454.

[7] 冯若.超声手册[M].南京：南京大学出版社，1999.

FENG Ruo.Ultsaronic Handbook[M]. Nanjing: Nanjing University Press,1999.

[8] 张小丽,林书玉,付志强,等. 弯曲振动薄圆盘的共振频率和等效电路参数研究[J]. 物理学报,2013, 62(3): 034301-1-034301-6.

ZHANG Xiaoli, LIN Shuyu, FU Zhiqiang, et al. Study on resonance frequency and equivalent circuit parameters of a thin disk in flexural vibration[J]. Acta Physica Sinica,2013, 62(3): 034301-1-034301-6.

[9] 李华. 超声波纵向振动内圆磨削系统的振子设计研究[J]. 金刚石与磨料磨具工程，1998，107(5):23—25.

LI Hua. Study on the vibrator design of the ultrasonic longitudinal vibration inner grinding system[J].Diamond & Abrasive Engineering,1998,107(5):23—25.

[10]范国良，应祟福，林仲茂,等. 一种新型的超声加工深小孔的工具系统[J]. 应用声学，1982，1(1):2—6.

FAN Guoliang, YING Chongfu, LIN Zhongmao,et al. A new ultrasonic tool system for the deep small hole machining[J]. Applied Acoustics,1982,1(1):2—6.

第十一届全国振动理论及应用学术会议通知

中国振动工程学会、中国力学学会、中国航空学会、中国机械工程学会和中国宇航学会为广泛开展学术交流，展示近年来原始创新和学科前沿的最新成果，探讨振动理论及应用的发展趋势，定于2015年11月5日至7日在北京举办第十一届全国振动理论及应用学术会议，会议由清华大学和北京航空航天大学承办。期间，将召开中国振动工程学会第八次会员代表大会，选举产生第八届理事会，同时举办2015年振动工程技术设备展览会。会议将邀请国内外著名专家作特邀专题学术报告。会议将出版论文集和光盘，并推选优秀论文在《振动工程学报》、《振动与冲击》等核心期刊发表。热忱欢迎振动工程领域科技工作者踊跃投稿并积极参会。

会议投稿时间节点详见会议网站。

The vibration characteristics and design of ultrasonic atomization system based on longitudinal-flexural vibration conversion

LIHua1，RENKun2，YINZhen1，ZHAOJiang-jiang2，CAOZi-yang1，LÜZi-qiang2

(1.College of Mechanical Engineering, Suzhou University of Science and Technology，Suzhou 215009，China；2.College of Mechanical and Electrical Engineering, Henan University of Technology，Zhengzhou 215009,China)

The new ultrasonic vibration atomization system composed of longitudinal vibration transducer and flexural vibration disc is proposed in this paper. The resonance characteristics and the design method of the new system are obtained through theoretical analysis and by FEM. It was shown by experiment that the new system mainly works in loading resonance state. The resonance frequency of the new system mostly depended on the structure of transducer. The output amplitude of the new system increases with the approaching of the resonance frequency between the longitudinal vibration system and the flexural vibration disc.

ultrasonic; vibration; atomization; longitudinal-flexural vibration conversion

2014-02-13；

2015-01-08

国家自然科学基金资助项目(51075288)

TG580.23+8

A

1004-4523(2015)03-0462-08

10.16385/j.cnki.issn.1004-4523.2015.03.017

李华(1961—),男，博士,教授。电话：(0512)69379088; E-mail: lihua@mail.usts.edu.cn