基于Matlab的某机场升降摆渡平台举升油缸铰点位置设计
赵子涵,贾英杰,刘宝波,李红勋,朱海天
(1.军事交通学院研究生管理大队,天津300161;2.军事交通学院,天津300161;3.军事交通学院国家应急交通运输装备工程技术研究中心,天津300161)
机场升降装卸摆渡平台主要用于实现集装箱以及其他航空货物的快速装卸,工作时通过升降装置改变输送平台的垂直高度,实现与机舱的对接,从而实现货物的水平输送,具有很高的工作效率,是机场地面物资装卸保障装备的重要组成部分[1]。
本文摆渡平台采用剪叉式举升机构,通过举升油缸的推动实现工作平台的升降。举升油缸的最大推力是举升机构极限工况一种体现,在满足性能要求的前提下,为提高各部件的使用寿命,要求油缸最大推力尽可能小一些。近些年来,寿旺洁[2]、齐文虎[3]、孙毅[4]等学者相继通过误试法、运动学及动力学分析等方式对剪叉机构的空间布置方案进行了研究,并取得了一定的成果,但整体看来,设计者经验的多少对设计结果影响很大。经过分析,本文首先选取直观性较强的虚位移原理对举升油缸的推力进行解析分析,借助Matlab定量研究相关设计参数对油缸推力的影响,进而引入空间布置要求及自身结构参数等作为边界条件,以确定举升油缸的最优布置方案,很大程度上减少了主观因素对设计结果的影响。
1 举升机构组成与工作原理
摆渡平台的举升机构采用剪叉式,从结构上看(如图1所示),举升油缸两端分别与剪叉臂、车架相连,内外剪叉臂之间通过销轴进行铰接,同时剪叉臂的一端通过销轴分别与车架或者工作平台的固定铰支座相连,另一端通过辊轴与车架或工作平台的滑槽相连。从运动形式看,剪叉机构的工作原理是将举升油缸的伸缩运动转化为辊轴的水平运动,进而通过剪叉臂转化为工作平台的垂直运动,最终完成货物的垂直升降。

图1 举升机构结构示意
2 油缸推力解析分析
为便于分析,取举升机构的1/2建立简化模型(如图2所示),各载荷也取实际值的1/2。其中,铰链的约束为理想约束,Q为负载、工作平台及剪叉臂自重之和的1/2,P为单组油缸的推力;E、F为油缸与剪叉臂以及车架的铰点,剪叉臂两端铰点的长度记为l,油缸活塞杆与剪叉臂的铰点与剪叉臂中心铰点的距离记为a,其他参数如图2所示。

图2 剪叉式举升机构力学模型
根据虚位移原理[5]可得

式中 Fxi、Fyi、Fzi、δxi、δyi、δzi分别为主动力及其对应的虚位移在坐标轴上的投影。
由式(1)可得

根据几何关系经变分运算可得

带入式(2)可得油缸推力的解析式为

设油缸的有效推力为Py,则Py在数值上等于总推力在竖直方向上的分量,即
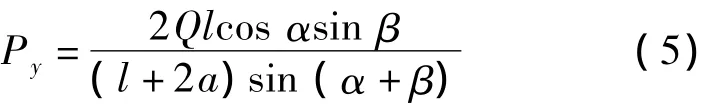
由式(4)可知,油缸推力P不仅与举升高度有关,还与油缸轴线与水平面的夹角β关系密切,而β的大小与反映举升油缸缸铰点位置的参数a有直接的关系。
3 举升作业仿真分析
3.1 举升作业数学模型的建立
由于摆渡平台自身结构及空间布置等因素的限制,举升油缸与车架的铰点F的可变范围较小,在分析中当作常量处理,着重对活塞杆与剪叉臂的铰点E的位置进行分析。
由图2中的几何关系可得
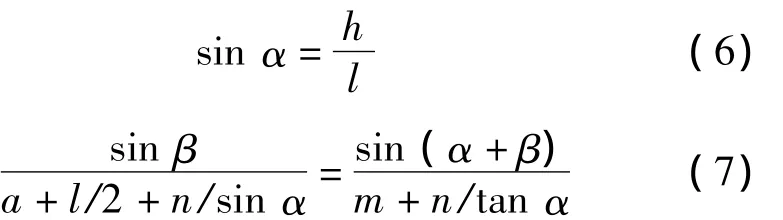
已知工作平台的举升高度为2.25~5.6 m,经换算,h∈(280 mm,3 630 mm)。经测量相关结构件的质量以及相关长度参数,对模型中的常量参数的取值如下:Q=1.393×105N;l=5 800 mm;m=5 000 mm;n=940 mm。由此建立了以式(4)为目标函数、式(6)和式(7)为约束函数、长度a为设计变量的数学模型。
3.2 基于Matlab的数值分析
在Matlab中编写程序,得到β、P以及Py关于变量a与h的三维曲线(如图3—5所示),为方便观察,分别输出 P、Py关于变量a与h的侧视图(如图 6、7 所示)。

图3 β关于参数a与h的变化曲线
由图3可知:在活塞杆铰接位置a一定时,举升油缸与水平方向的夹角β随举升高度的增加非线性变大;在举升高度h一定时,β随参数a的增加非线性变大,与实际情况相吻合。
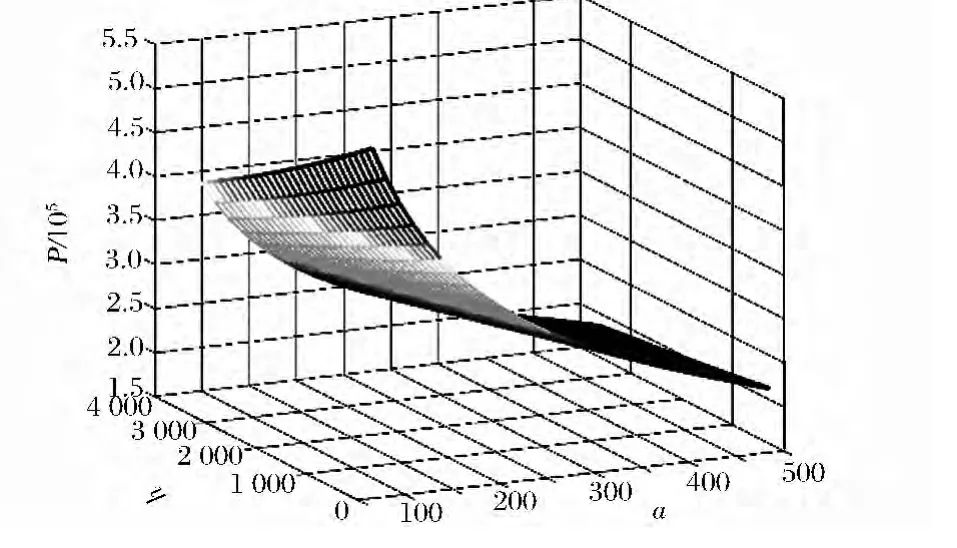
图4 P关于参数a与h的变化曲线

图5 Py关于参数a与h的变化曲线

图6 P关于参数a与h的变化曲线(侧视图)
由图4—7可知:当活塞杆铰接位置(参数a)确定时,随着举升高度h的增加,举升油缸推力逐渐减小,并逐渐趋于平缓;当举升高度h一定时,随着活塞杆铰接位置远离剪叉臂铰点中心(即参数a增大),举升油缸的推力随之非线性减小,并逐渐趋于平稳。
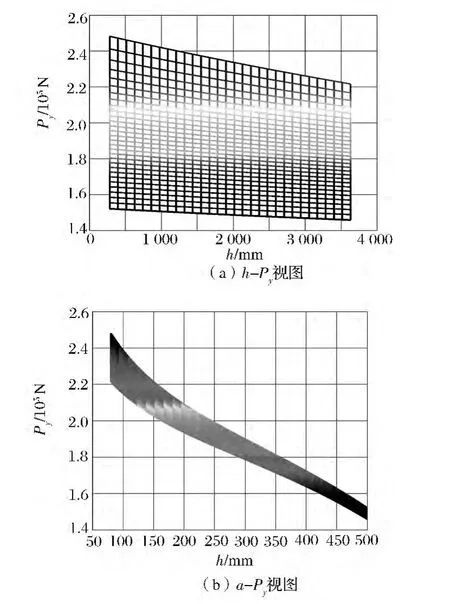
图7 Py关于参数a与h的变化曲线(侧视图)
理论上来说,举升油缸的有效推力取决于负载,但是在举升过程中,随着举升高度的变化,剪叉臂受到的支反力是不断变化的,因此,在举升过程中举升油缸有效推力Py会呈现图5的变化。
综上可得出结论如下:工作平台位于最低位置(即h=280 mm)时举升油缸的受力最大;在举升高度一定时,油缸的推力P与油缸铰点位置a存在非线性对应关系。
下面对工作平台位于最低举升位置时的工作状态进行研究。取 h=280 mm,a∈(-500,1 000),在Matlab中编写程序,结果如图8所示。

图8 最低举升位置时油缸推力关于a的变化
由图8可知,在举升高度最低时,随着参数a取值的增大,举升油缸推力以及有效推力均不断减小,且变化趋势逐渐趋于平缓。因此,理论上来说a应取最大值。但是在实际情况中,举升油缸的布置除了要考虑载荷、行程、油压及压杆稳定等因素外,还需要考虑与其他部件的位置关系,要求各部件之间在运动过程中不能产生干涉。为进一步确定参数a的取值范围,下面添加油缸行程与其结构尺寸的关系作为新的约束条件。
摆渡平台采用闭式液压系统,其系统压力在25 MPa左右,查阅《机械设计手册》[6],初选液压缸缸径D=160 mm,杆径d=120 mm。在设计的初级阶段,一般对高压油缸的行程采取以下保守估计:
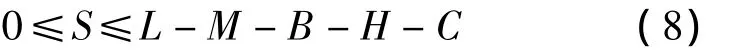
式中:S为举升油缸的行程;L为举升油缸最小安装距;M为缸底厚度(取D/2);B为活塞宽度(取D);H为导向套长度(取D);C为其他结构长度(包括绞耳、活塞杆外露长度)等。
由此,得出新的边界条件:

如图9所示,A1O1B、A2O2B分别为举升过程中剪叉臂的极限位置。记|FE1|为f1(a),表示工作平台处于最低点时举升油缸长度(最小安装距);|FE2|为f2(a),表示工作平台处于最高点时液压缸总长度。

图9 举升油缸极限位置示意
由几何关系可得

则油缸行程L=f2(a)-f1(a)。由式(9)可建立以为目标函数,以a为设计变量,以式(7)为约束函数的数学模型,经作图法得 α1=3°,α2=39°。记:

在Matlab中编写程序,分别画出目标函数关于参数a的变化曲线(如图10所示)。
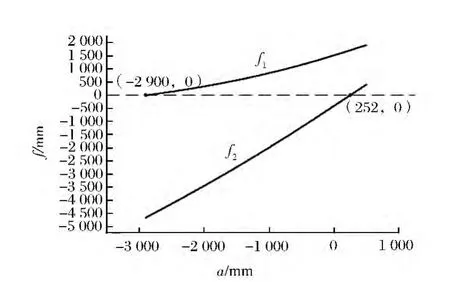
图10 满足举升油缸结构参数要求的a取值范围
由图10可知,满足以举升油缸结构尺寸为约束条件的参数 a取值范围为(-2 900 mm,252 mm)。其中,负值表示油缸活塞杆的铰点位置在剪叉臂的下半段,这些位置虽然在理论计算上满足条件,但会导致β角偏小,在负载一定(液压缸有效推力Py一定)的情况下,举升油缸的推力P变大,进而影响油缸的使用效率与使用寿命。
在保证举升油缸最大推力尽可能小的前提下,综合考虑整体布置,做到各部件之间不产生干涉,最终确定a=240 mm,设计结果见表1。

表1 举升油缸活塞杆铰点位置设计结果 mm
3.3 举升油缸的流量设定
工作平台的举升速度由举升油缸运动速度决定,两者均是剪叉臂与水平方向夹角的函数。根据虚位移原理得
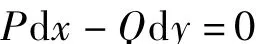
等式两边对时间进行求导得

与式(4)联立可解得油缸运动速度Vp与平台上升速度Vy的关系为
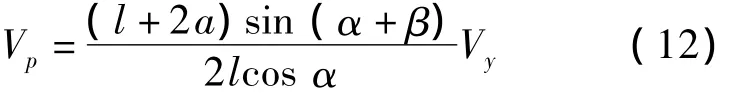
由式(12)可知Vp与Vy存在非线性关系,且类似于载荷关系曲线,当油缸运动速度恒定时,平台上升速度也是不断变化的。由于机场升降平台类装备的举升速度一般较小,在工程实践中为便于控制,一般将油缸运动速度设置为定速[7]。
根据指标要求平台举升速度为250 mm/s,则举升油缸运动速度为mm/s(S为油缸行程,H为举升高度),由此可计算平台平台举升油缸的单缸流量为
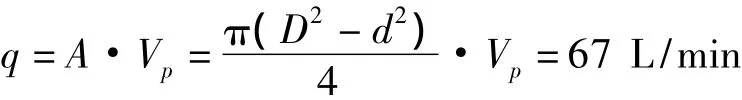
则举升油缸的双缸流量为134 L/min。
4 结语
本文通过理论分析建立了摆渡平台举升机构的数学模型,运用Matlab对举升作业过程中的油缸受力进行了解析分析,结果表明油缸的铰点位置与油缸推力存在非线性对应关系。在满足空间布置要求的基础上确定了以油缸受力最小为设计目标的铰点布置方案,并对油缸行程、流量设定等参数进行了计算。本文采用的设计方法和理念也适用于其他机构的参数化最优设计。
[1] 詹隽青.28t机场升降装卸摆渡平台论证报告[R].天津:军事交通学院,2011.
[2] 寿旺洁.剪叉式液压升降台参数化设计及结构分析[J].工程技术,2010(14):20-23.
[3] 齐文虎.液压缸双梁铰接式剪叉升降平台布置方式优化设计[D].兰州:兰州理工大学,2011:6-7.
[4] 孙毅.对称驱动剪叉式升降平台设计及研究[D].昆明:昆明理工大学,2012:3-10.
[5] 段慧文.剪叉机构计算与虚位移原理[J].演艺科技,2012(5):33-37.
[6] 闻邦椿.机械设计手册[M].5版.北京:机械工业出版社,2010:5-13.
[7] 詹隽青.军用特种车辆结构与设计[M].北京:国防工业出版社,2003:26-37.

