IRF4115S型MOSFET电路板有限元热分析

柴树峰，张学玲，李春卉，任保全

(1.军事交通学院军事物流系，天津300161;2.北方通用动力集团有限公司六一六厂舰船动力部，山西大同037036)

MOSFET管(简称MOS管)使用中，散热是十分突出的问题。由于MOS管需要流经大电流，因此内部温度会快速升高，尤其是在MOS管的并联电路中，某个功率管瞬时可能会承载所有负载电流，一旦温度超出了工作范围，将引起MOS管工作不稳定甚至烧毁。利用金属铝基印制板可有效地解决散热问题，将排列均匀的MOS管焊在铝基板上，热量通过铝基板和导热硅胶传送到底座铝板上散热，从而使印制板上不同材质、不同类型元器件的热胀冷缩问题得到缓解，提高整块电路板和电子器件的耐用性和可靠性。

在MOS管的使用中，热设计和散热技术研究受到人们广泛重视。国内外在这方面已进行了一些研究，热设计和散热技术研究的基础是对MOS管热特性的准确测量和分析［1－2］。实验测量可在接近组件使用条件下进行，具有精度高和数据可靠等优点;但仅能确定MOS管表面和内部有限几个点的温度，而且，需要制造样件和较复杂的测量仪器，费工费时，需较长的设计周期。数学分析方法虽然可利用设计版图的几何信息和材料物理参数预估产品的热性能，为设计人员改进设计方案提供参考和依据，但由于铝基板结构较复杂，工艺参数和边界条件难以准确模拟;如果采用简化的数学模型，就使计算精度和分析结果的可靠性降低，因此数学分析方法也不可靠。

为解决MOS管的局部高温引起的热可靠性问题，本文提出利用有限元方法，建立铝基板的三维有限元热分析模型，在有限元软件中进行求解计算，得到整个铝基板的温度场分布云图、热应力和热变形云图，以验证该功率板散热性能的热可靠性情况。

1 热分析和热变形分析理论

热变形原理非常复杂，目前只能在微观上给予定性解释。固体材料的热膨胀本质上可归结为点阵结构中各点平均距离随温度的升高而增大。德拜(Debye)理论［3］认为，各原子间的热振动相互牵连制约，随着温度的升高，各质点的热振动加剧，质点间的距离增大，在宏观上表现为晶体膨胀现象。热变形与材料的热膨胀系数、温度等参数密切相关。在解决实际工程问题时，有时热传导状况非常复杂，尤其是移动持续热源引起的热变形量计算，由于温度分布函数相当复杂，按常规方法求解十分困难。

有限元法是随着计算机的发展而兴起的一种数值计算方法，将元件模型划分为若干个网格，设定边界条件进行求解。而对于温度场的有限元计算实际是对温度场微分方程相应的泛函数求极值的过程。采用有限元法进行热变形分析能使计算大为简化［4－5］。

热分析是基于能量守恒原理的热平衡方程，可以用有限元法计算出节点的温度，并导出其他热物理参数。结合CAE软件能够计算出局部空气流通的情况以及温度分布情况，得到比传统计算方法更加精确的数据，从而更好地进行结构的散热设计。

ANSYS热分析包括热传导、热对流及热辐射3种传导方式［6］。在绝大多数情况下，热传导分析问题都带有对流和(或)辐射边界条件。ANSYS热分析主要有稳态传热分析和瞬态传热分析两大类。

如果系统的净热流率为0，即流入系统的热量加上系统自身产生的热量等于流出系统的热量:q流入+q生成－q流出=0，则系统处于热稳态。在稳态热分析中任何节点的温度都不随时间变化。稳态热分析的能量平衡方程的矩阵形式为

式中:K为传导矩阵，包含导热系数、对流系数及辐射率和形状系数;T为节点温度向量;Q为节点热流率向量，包含热生成。

瞬态传热过程是指一个系统的加热或冷却过程。在这个过程中系统的温度、热流率、热边界条件以及系统内能随时间都有明显变化。根据能量守恒原理，瞬态热平衡的矩阵形式为

式中:C为比热矩阵，包含系统内能的增加;˙T为温度对时间的导数。

ANSYS利用模型几何参数、材料热性能参数以及所施加的边界条件，生成K、T和Q。当研究MOS管在恒定负载工作时的稳态温度场时，需要把有限元模型的热源假设为恒定，进行稳态传热分析。MOS管电路板在生热、散热过程中，产生的热由MOS管传导到铝基板和底座，再由底座通过辐射散热，当发热量和散热量相当时，温度处于稳定状态。

2 IRF4115S型MOS管电路板的有限元模型和分析参数

本文设计的铝基板散热结构是将3组(每组10只，上、下桥臂各5只)IRF4115S型MOS管排列均匀地焊接在铝基板上，其电路板和底座材料为铝，电路板与散热有关参数见表1。每组MOS管都有两种工作状态:“上桥臂导通，下桥臂关断”，称为“1”状态;“下桥臂导通，上桥臂关断”，称为“0”状态。3个桥臂只有“1”或“0”两种状态，因此3组 MOS管共有8种组合方式:000、001、010、011、100、101、110、111。选择组合方式 101为例:第1组上桥臂5只 MOS管导通，共发热18.75 W;第2组下桥臂5只MOS管导通，共发热18.75 W;第3组上桥臂5只MOS管导通，共发热18.75 W;设正极、负极和三相铜柱的发热分别为10、5、10 W，初始温度为25℃。本文选择101、110、010、100四种组合方式进行分析。

表1 IRF4115S型MOS管电路板散热有关参数

按照实际尺寸建立铝基板、发热元件和底座铝板的整体几何模型。利用ANSYS软件进行有限元分析，由于建立的铝基板模型是规则的长方体形状，所以采用适合规则长方体形状划分的20节点的三维实体热单元SOLID90节点单元。在定义单元类型、材料属性、建立三维模型后，对该模型进行网格划分。为保证计算精度又考虑整个模型的计算量，在进行网格划分时对MOS管重点关注的区域选取较密的单元进行划分，对于底座铝板采用较疏的网格划分。进行网格划分后的有限元模型如图1所示。101组合方式的MOS管工作发热时的有限元模型边界条件如图2所示。

图1 铝基板散热结构有限元模型

3 有限元仿真

3.1 热分析

电路板长时间工作会发热，当温度超过80℃时，电路板会断电保护。因此，希望在使用时间内电路板温度不会超过80℃。由于工作时间较长，属于热稳态分析。分别在不同散热条件下(自然条件、通风条件好、有散热风扇、专门设备散热)，计算各组合元件工作时的稳态温度分布，以及最坏散热工况下即最高温度下的热变形。

自然散热条件下、稳态工作时，101组合方式温度分布如图3所示，温度等高线分布如图4所示，热流率分布如图5所示。

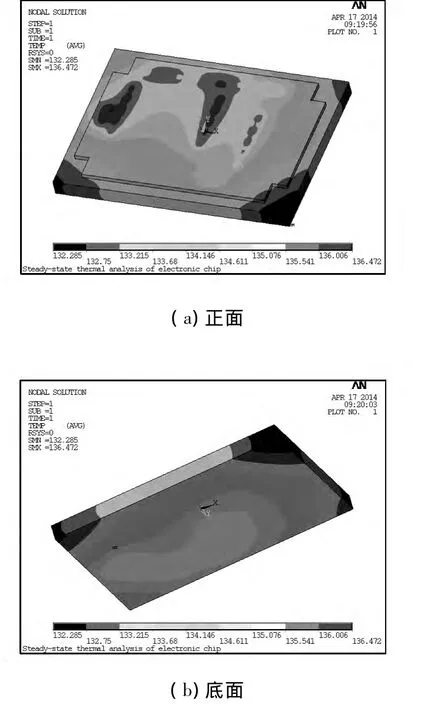
图3 自然散热条件下101组合元部件工作温度分布(℃)

图4 自然散热条件下101组合元部件温度等高线分布(℃)

图5 自然散热条件下101组合元部件热流率分布(W/m2)

各组MOS管交替工作时，温度分布相近。随散热条件改善，电路板稳态温度会下降。在不同散热条件下的101组合元部件工作时热分析结果见表2。

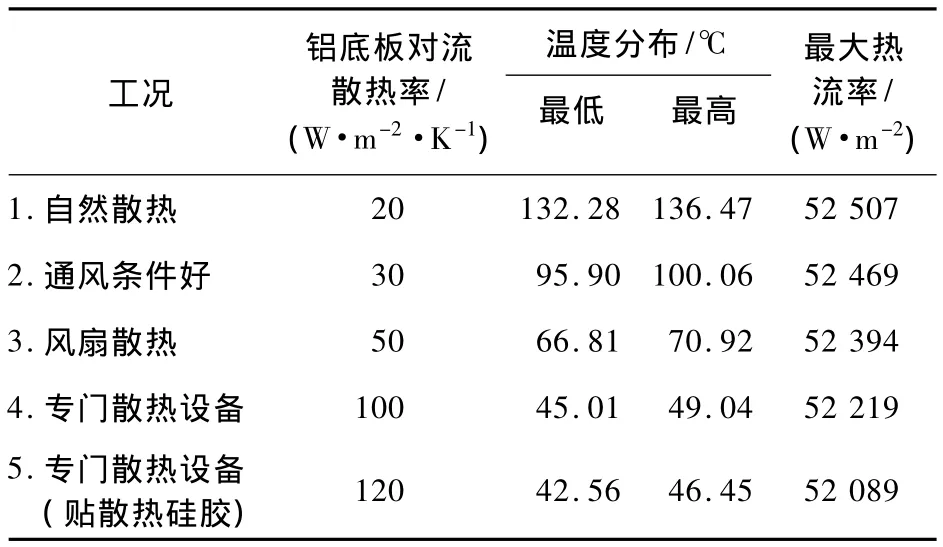
表2 热分析结果

由表1中的热分析温度分布情况，可以得到不同散热条件下的温度分布曲线图(如图6所示)，可以看出:在自然散热和通风条件好工况下，电路板温度高于正常工作温度，电路板不能正常工作;在风扇散热工况下，能够满足使用温度要求;随着通风状况的改善，铝底板对流散热率提高，电路板温度随之下降，当铝底板对流散热率提高到一定程度时，电路板温度下降不明显;设计的电路板散热均匀，最高和最低温差在4℃左右。

图6 不同散热条件下温度分布曲线

3.2 热应力和热变形分析

发热能使电路板膨胀，引起变形，如果变形过大会使电路失效。计算在通风良好条件下的热应力和变形。由于101、110、010、100四种组合方式工作时的发热量相当，所以只计算101组合工作时的热变形。

当铝基板底面约束时(底面粘到固定位置处)的热应力云图和热变形云图如图7所示。

图7 底面约束时的热应力和热变形云图

当铝基板用四角螺栓固定时的热应力云图和热变形云图如图8所示。

图8 四角螺栓固定时的热应力和热变形云图

通过热应力云图和热变形云图可以看出:当铝基板底面约束时，最大变形量为0.662×10－4m，铝 基 板 边 缘 最 大 热 应 力 为81 MPa，底板边缘工作区域应力约为 0.11～9.07 MPa，其他部分变形均匀，最大变形量相对于铝基板尺寸(210 mm)所占比例为0.031%;当四角螺栓固定时，最大变形量在螺栓紧固处，为0.510×10－5m，最大热应力为247 MPa。两种情况都不会影响电路板失效，可以看出热应力与热变形对铝基板影响非常小。

4 结论

(1)整个电路板的散热均匀，最高和最低温差在4℃左右。功率最大、长期工作、自然散热条件下，最高温度136℃，不满足使用要求，改善散热条件，如加风扇、散热硅胶等可达到要求。

(2)电路板热变形量很小，仅为电路板尺寸的0.031%，不会发生热变形失效。

(3)本次仿真分析是在最差工况下计算得到的，通过改善散热环境，电路板温度还可以进一步降低，变形量也可以进一步减小。根据以上温度场和整体的热负荷分析，可以证明，该功率板的散热性能是在允许范围内的，功率板的设计是合理的。

［1］ 吴根盛.电动车用DC/DC电源模块有限元热分析研究［J］.汽车实用技术，2013(3):10-16.

［2］ 孙利杰.热分析方法综述［J］.科技资讯，2007(9):17.

［3］ 苗恩铭，费业泰，赵静.温度、热量与热变形的关系及计算方法研究［J］.工具技术，2003(7):19-21.

［4］ 杨玉龙，关富玲，张淑杰.可展桁架天线温度场和热变形分析［J］.空间科学学报，2005，25(3):235-240.

［5］ 赵宁，孙晓玲，陈国定，等.双圆弧齿轮传动的有限元热分析［J］.现代制造工程，2006(4):50-52.

［6］ 王泽鹏，张秀辉，胡仁喜.ANSYS12.0热力学有限元分析从入门到精通［M］.北京:机械工业出版社，2010:1-20.