基于SimuEngine的船艇主机仿真

张 锦，聂 伟，沈 军

(镇江船艇学院动力指挥系，江苏镇江212003)

船艇主推进装置是一个复杂系统，分析、研究其稳态和动态特性，对其维护、管理和故障诊断，对机电管理具有重要的意义。长期以来，船艇部队一直依赖实船完成机舱装备的培训和训练，培训手段单一、周期长、效率低、成本高，且训练质量得不到保证，某些重点课目甚至无法进行训练，导致船艇效能难以发挥，制约了船艇部队战斗力的提升。

通过建模技术建立船艇主推进装置的数学模型，并通过计算机仿真技术来实现用于仿真训练的机电模拟器，一直是航海类院校和科研院所的重点研究内容。建立能够反映船艇主机及系统特性的仿真模型，具有重要的科学意义和经济效益。通过模拟器的仿真操作和训练，可使学员快速掌握真实对象的组成、工作原理和工作特性，并能准确地对其进行故障诊断，而不必像实装训练那样花费很大的人力、财力和时间［1－3］。此外，仿真系统还可以完成实装训练无法做到或十分危险的实验(如大风浪航行、拉缸、飞车等)。

本文提出一种不牺牲精度又能满足实时性要求的建模和仿真方法，给出以某型船艇主推进装置为主要仿真对象的实时仿真模型;建立该型艇主机的仿真模型，并应用于该型艇主机及其系统的模拟训练装置。该模拟训练装置以陆空军船艇某主力船型机电系统为仿真对象，建成一个可开展船艇主机及推进系统、船艇电站、船艇辅助机械、机舱集控、主机遥控、机舱综合管理等课目训练的模拟系统，可以进行船艇机电专业人员的技能培训，尤其是完成一些实装难以实现的训练，如机舱报警情况下的随船应急处置等模拟训练。

1 船艇主机仿真系统支撑环境

仿真支撑环境是以计算机设备为载体，为训练人员提供一个输入输出界面，并通过此界面与数学模型联系起来［4］。在仿真支撑环境的支持下，计算机和专用物理效应设备的操作信息传递给在后台运行的数学模型，运行结果及时在计算机交互界面和硬件仪表上显示，系统结构组成框图如图1所示。

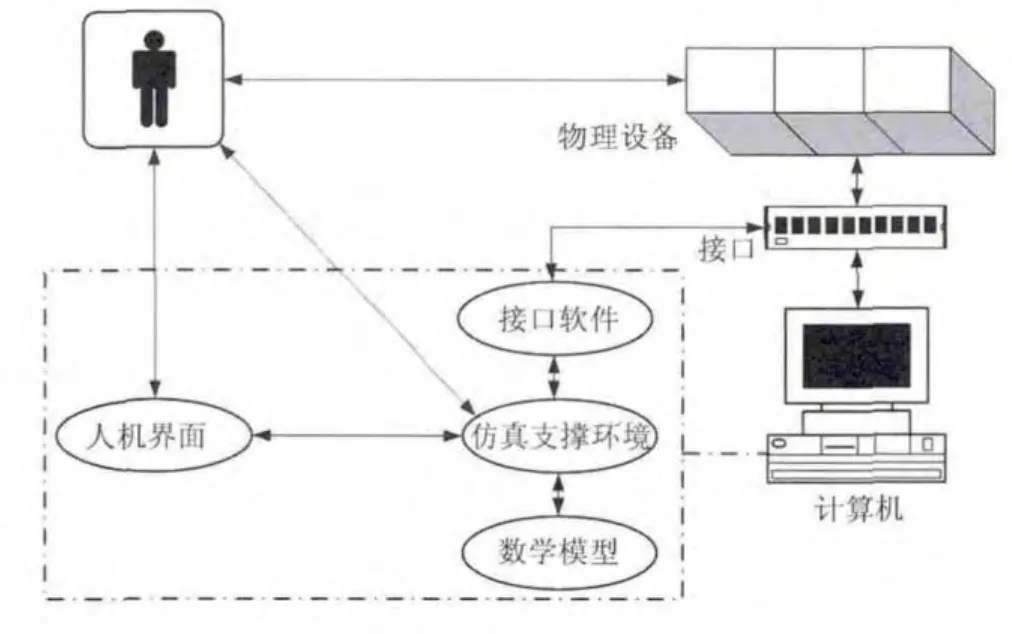
图1 船艇主机仿真系统结构组成框图

主机系统仿真支撑环境选用SimuEngine可视化仿真支撑系统，该系统具有独立自主知识产权，可采用Fortran语言编写程序。系统的主窗口集成了数据动态显示、变量数据库管理、多任务管理、仿真过程实时控制等功能。SimuEngine系统由数据库管理系统、模型开发支持系统、模型调试与试验分析系统、实时运行与多任务调度系统、指导员功能、网络通信系统、API接口与OPC接口等功能部分组成。

2 仿真模型建立与求解方法

主机系统的数学模型必须适用于各种模拟训练工况，包括主机的启动、停止、工况转换及故障运行等，且主机模拟训练系统应具有较高的实时性。为了减少过于耗时的计算，在满足精度前提下，仿真系统中一般采用计算量小的算法并且需要对模型做一些简化。

主机系统各模块的结构有其相对的独立性，各模块动态性能的描述都采用微分方程形式，而稳态性能一般采用代数方程描述。对于时间常数很小的动态过程，则采用准稳态近似法进行模型简化。描述连续系统最基本的数学工具是微分方程或状态空间方程，由这两类模型可以导出其他模型。把已建立主机系统数学模型转换成仿真运算模型，但主机系统的数学模型相对复杂，求其解析解是很烦琐、很困难的，大多数情况求不出解析解，或者根本不存在解析解，因此，必须借助于数值解法对连续系统进行仿真研究［5］。连续系统的数值积分法，就是利用数值积分方法对常微分方程(组)建立离散形式的数学模型——差分方程，并求其数值解。在数字计算机上构造若干个数字积分器，利用这些数字积分器进行积分运算。在数字计算机上构造数字积分器的方法就是数值积分法，而数字机的硬件特点决定了这种积分运算必须是离散和串行的。

对主机系统仿真模型中常微分方程的计算，包括非线性及变系数的常微分方程，主要采用数值方法求解，主要算法包括欧拉积分法(Euler)、龙格－库塔法(Runge－Kutta)、亚当姆斯法(Adams)等。

3 仿真结果分析与模型验证

3.1 仿真步长的选择

在仿真过程中，步长的选择十分重要。步长太大会增加截断误差，步长太小不但增加计算的次数，还会增加误差，运算一次出现一次误差，最终导致误差不断增大，同时还会增加计算的复杂程度。在一般情况下，步长改变对平稳变化变量的总误差影响较小，但对变化比较剧烈的变量，步长改变对积分运算所产生的误差就有很大影响。因此，在确定积分方法之后，选择积分步长就要考虑变量的变化程度，对变化剧烈的变量应尽可能选择高阶的计算方法，积分步长要选择较小的。在选择仿真算法时还要考虑计算速度，有些仿真问题(如实时仿真)对计算速度的要求比较高。计算速度主要取决于每步运算所花费的时间及计算的总次数，而每步的计算量又与所选择的具体算法、函数的复杂程度、每步积分所要计算函数的次数有关。一般说来，要提高仿真算法的计算速度，就要增加仿真步长，但增加步长又会导致误差增大，所以，要提高计算速度必须在保证精度的前提下增大步长，以便缩短计算时间［6］。

3.2 仿真研究及模型验证

本仿真对象主要是船艇柴油发电机系统、推进系统及其控制系统。因此，需要综合考虑船艇推进系统的不同工况，设定不同的仿真参数，如艇体附水系数、阻力系数等［7］。典型航行工况的仿真计算流程如图2所示。

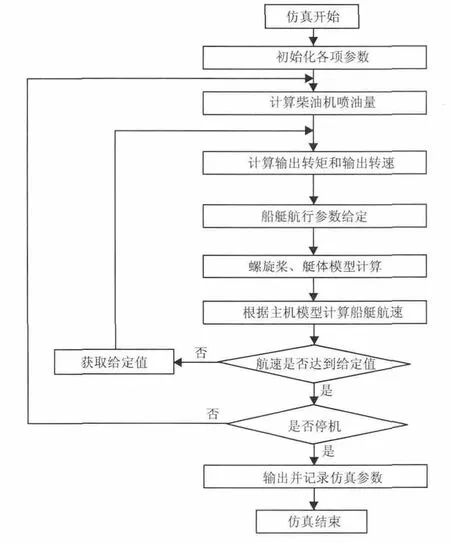
图2 主机系统航行工况仿真计算流程

船艇在稳定航行过程中，推进系统各性能参数是渐进变化的，短时间内可认为系统是稳定的，在对整个航行过程进行仿真时，可认为主机系统是以准稳态的方式工作，仿真计算时将这两种航行过程分成有序的时间间隔，并逐步递推得出其在各时间间隔点上的状态参数。图3为柴油机启动过程的动态仿真曲线。图中参数值已进行无量纲化处理。

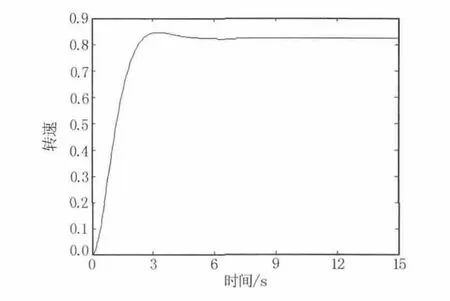
图3 柴油机启动过程的动态仿真

在船艇航行工况仿真时，柴油发电机组模型将参与仿真运算。图4为柴油机加速到一定转速后突加负荷时，柴油机转速、发电机功率及电流等性能参数的仿真曲线。图中参数值均已进行无量纲化处理。

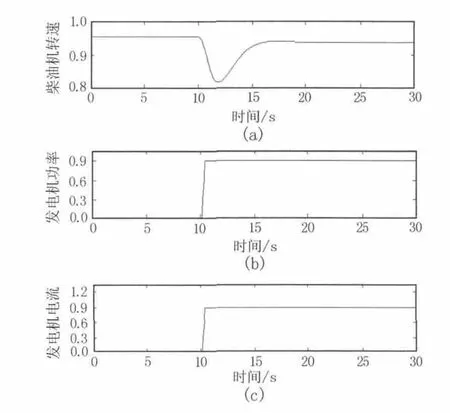
图4 突加负载时机组性能参数的变化

图5 所示为螺旋桨阻力矩随转速变化的曲线，其阻力矩先成抛物线上升，当转速稳定后，则成一条直线。仿真结果与实测值能较好吻合，其动态仿真过程与实测值较为相符，转速、输出转矩等参数的稳态值与实测值的误差在5%之内，表明仿真模型满足系统的精度要求。图中参数值均已进行无量纲化处理。

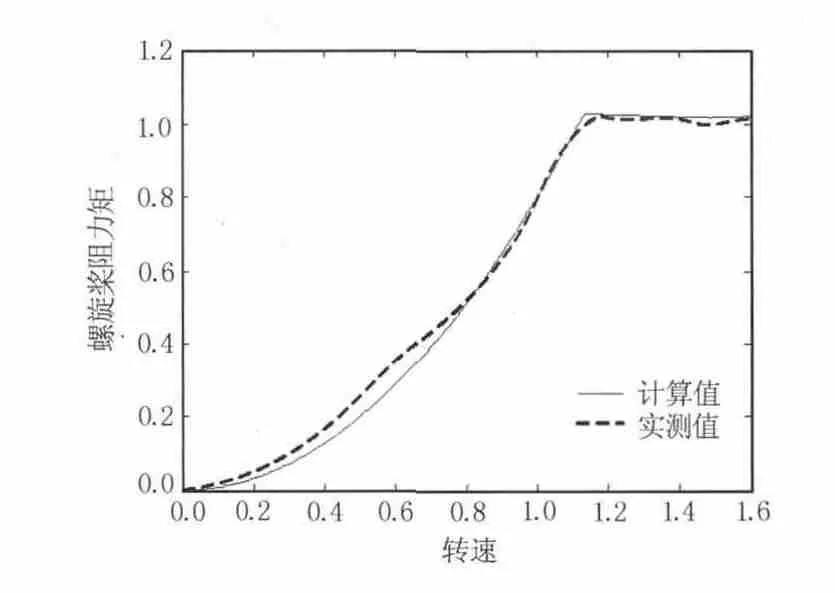
图5 航行工况螺旋桨阻力矩随转速的变化

在系统模型中，还包含体现设备自动控制、联锁、保护等逻辑数学模型，这些模型是完成主机系统仿真的重要组成部分，因此，需要对其进行验证。仿真表明，主机系统的联锁、保护等控制逻辑与实艇完全一致，控制器功能符合各设备的实际控制规律。

4 结语

以某型艇主机为研究对象，提出了主机建模和仿真方法，建立了主要仿真对象的实时仿真模型，模拟了该型艇主机的工作特性，研究结果已经应用于模拟训练装置。

［1］ 吴杰长，庞之洋，梁述海.基于仿真支撑系统和组态软件平台的舰船轮机仿真训练模拟器研究［J］.系统仿真学报，2004，16(3):605-607.

［2］ 郑华耀.基于网络化技术的大型集装箱船舶轮机模拟器［J］.系统仿真学报，2001，13(6):723-725.

［3］ 曹辉，张均东.现代船舶轮机模拟器的应用与发展［J］.航海教育研究，2012(1):33-36.

［4］ 冯国胜，杨绍普.柴油机及其电控系统仿真［J］.系统仿真学报，2005，17(9):2276-2279.

［5］ 黄曼磊，唐嘉亨，郭镇明.柴油机调速系统的数学模型［J］.哈尔滨工程大学学报，1997，18(6):20-25.

［6］ 薛定宇，陈阳泉.基于Matlab/Simulink的系统仿真技术与应用［M］.北京:清华大学出版社，2002:87-96.

［7］ 钟欣，肖民.船舶轴带发电机系统的建模与仿真［J］.华东船舶工业学院学报(自然科学版)，2005，19(4):15-18.