Mackey-Glass时滞系统的稳定性与混沌控制
杨纪华,李艳秋
(1.宁夏师范学院数学与计算机科学学院,宁夏 固原 756000;2.南京工业大学理学院,江苏 南京 210009)
Mackey-Glass时滞系统的稳定性与混沌控制
杨纪华1,李艳秋2
(1.宁夏师范学院数学与计算机科学学院,宁夏 固原 756000;2.南京工业大学理学院,江苏 南京 210009)
研究了时滞对Mackey-Glass系统动力学的行为影响和混沌控制. 首先,时滞反馈控制不能使系统的零平衡点控制为稳定的. 对于非零平衡点,从系统线性化方程的特征方程根的分布入手,分别研究了具有单时滞和双时滞系统的线性稳定性. 发现当系统中的时滞经过一系列临界值时,系统经历了Hopf分支. 其次,应用时滞反馈控制方法,选择合适的反馈增益和时滞使系统在不稳定非零平衡点附近出现周期轨. 最后,通过数值模拟检验了理论结果.
稳定性;Hopf分支;混沌吸引子;混沌控制;周期轨
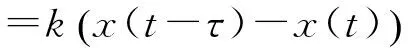
考虑Mackey-Glass模型[3]
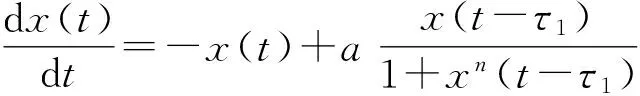
该系统最初是用来描述白细胞繁殖的模型,后来成为混沌理论中超混沌系统的典型代表,其中x(t)表示血液循环中成熟细胞的质量分数,τ是在骨髓中产生未成熟细胞和在血液中释放成熟细胞的时滞参数,a为系统的反馈率,n是正常数.如需要其详细的生物学意义,请参考文献[3-6]. 在文献[7]中利用中心流形定理和规范型理论讨论了离散时滞Mackey-Glass系统的动力学性质,并研究了当参数经过一系列临界值时Neimark-Sacker 分岔的稳定性与方向.在文献[8]中,作者对于二维时滞微分方程进行了研究,并分别通过单向和双向耦合实现了混沌同步. 本文应用时滞反馈控制方法研究具有双时滞的Mackey-Glass模型
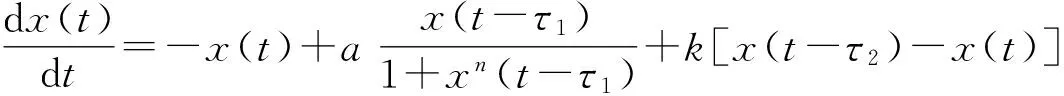
(1)
其中k为反馈增益,τ2是时滞. 本文中a>1,n>0,k>0.
1 平衡点的稳定性和Hopf分支的存在性
λ+1+k-ae-λτ1-ke-λτ2=0.
(2)
定理1.1 对任意的k和τ2,系统(1)的平衡点x0=0都是不稳定的.
证明λ=u+iv(v>0)为方程(2)的根的充分必要条件是
(3)
显然v=0是方程组(3)中第二个方程的根. 令
F(u)=u+1-ae-uτ1+k(1-e-uτ2),
可得
F(0)=1-a<0,F(a)=1+a(1-e-aτ1)+k(1-e-aτ2)>0.
由介值定理,存在u0∈(0,a)使得F(u0)=0,即方程(2)至少有一个具有正实部的根. 因此系统(1)的平衡点x0是不稳定的. 定理得证.
下面仅讨论系统(1)在平衡点x1处的情形,点x2处可类似论证.系统(1)在平衡点x1处的特征方程为
φ(λ)=λ+1+k-be-λτ1-ke-λτ2=0,
(4)
引理1.1 当τ1=τ2=0时,方程(4)的所有根具有负实部.
下面我们分两种情形论证引理1.1的结论.
第一种情形:τ2=0.
此时,特征方程(4)变为
ψ(λ)=λ+1-be-λτ1=0.
(5)
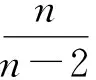
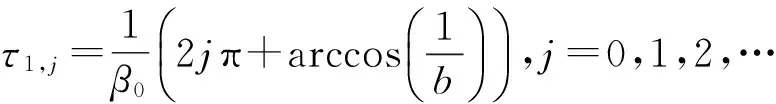
(6)
证明λ=iβ(β>0)是方程(5)的根当且仅当β满足
从而可得
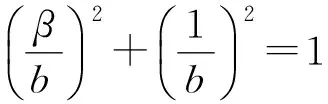
(7)
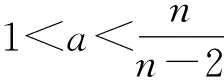
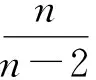
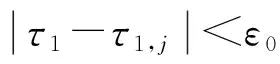
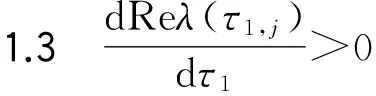
证明 对方程(5)两端同时关于τ1求导得
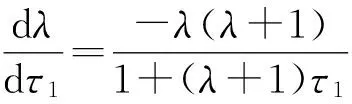
所以
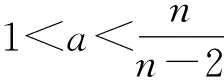
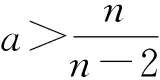
证明 由引理1.2可得结论(ⅰ)正确. 由引理1.3,当τ1∈[τ1,0,+∞)时,特征方程(5)至少有一对具有严格正实部的根,故当τ1∈[0,τ1,0)时,系统(1)的零平衡点是局部渐近稳定的;当τ1∈[τ1,0,+∞)时,系统(1)的零平衡点是不稳定的. 由文献[10]中关于泛函微分方程的Hopf分支定理可得结论(ⅱ)成立.
第二种情形:τ2≠0.
为方便起见,记
g(ω)=b2+ω2+2k+1-2b(1+k)cosτ2ω+2ωbsinτ2ω.
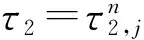
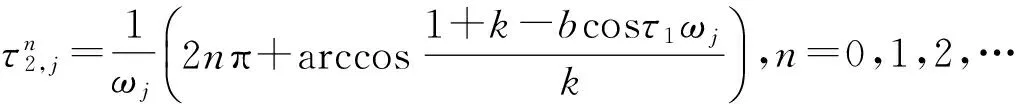
(8)
证明 设iω(ω>0)是方程(4)的根,则
(9)
由此
b2+ω2+2k+1-2b(1+k)cosτ1ω+2ωbsinτ1ω=0.
(10)
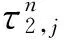
记
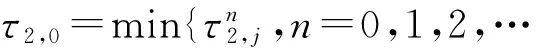
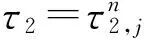
引理1.5 如果ω0τ1cosω0τ2,0+(1+τ1+kτ1)sinω0τ2,0≠0,则
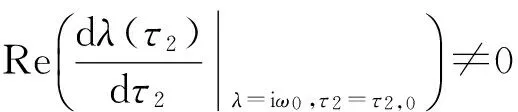
证明 方程(4)两端同时关于τ2求导得
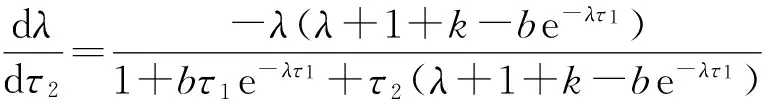
所以
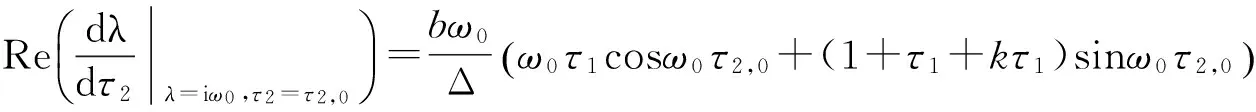
其中
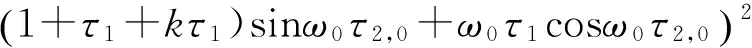
因为ω0τ1cosω0τ2,0+(1+τ1+kτ1)sinω0τ2,0≠0,所以
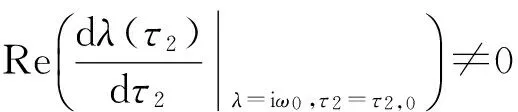
由本文引理1.2至引理1.5和文献[10]中第11章定理1.1,可以得到下面关于系统(1)的平衡点的稳定性与Hopf分支的存在性定理.
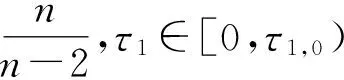
2 混沌控制分析
本小节讨论怎样选择合适的控制参数k和τ2,使得系统(1)不稳定的平衡点在其一个领域内控制为周期解.
证明 对任意的正数r,定义Γ=Γ1∪Γ2,其中
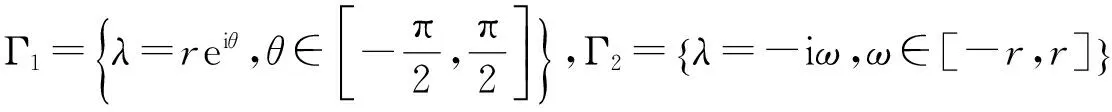
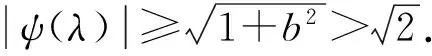
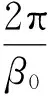
3 数值模拟
例3.1 在系统(1)中取a=2,n=10,τ2=0,通过简单计算可得τ1,0≈0.604 6. 根据定理1.2,当τ1=0.3时,系统(1)的平衡点是局部渐近稳定的;当τ1=0.6时,系统(1)经历了Hopf分支,如图1所示;当τ1=10时,系统(1)的平衡点是不稳定的,且出现了混沌吸引子,如图2所示.
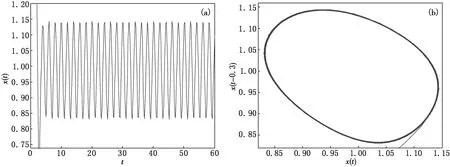
图1 当τ2=0,τ1=0.6时,系统(1)经历了Hopf分支
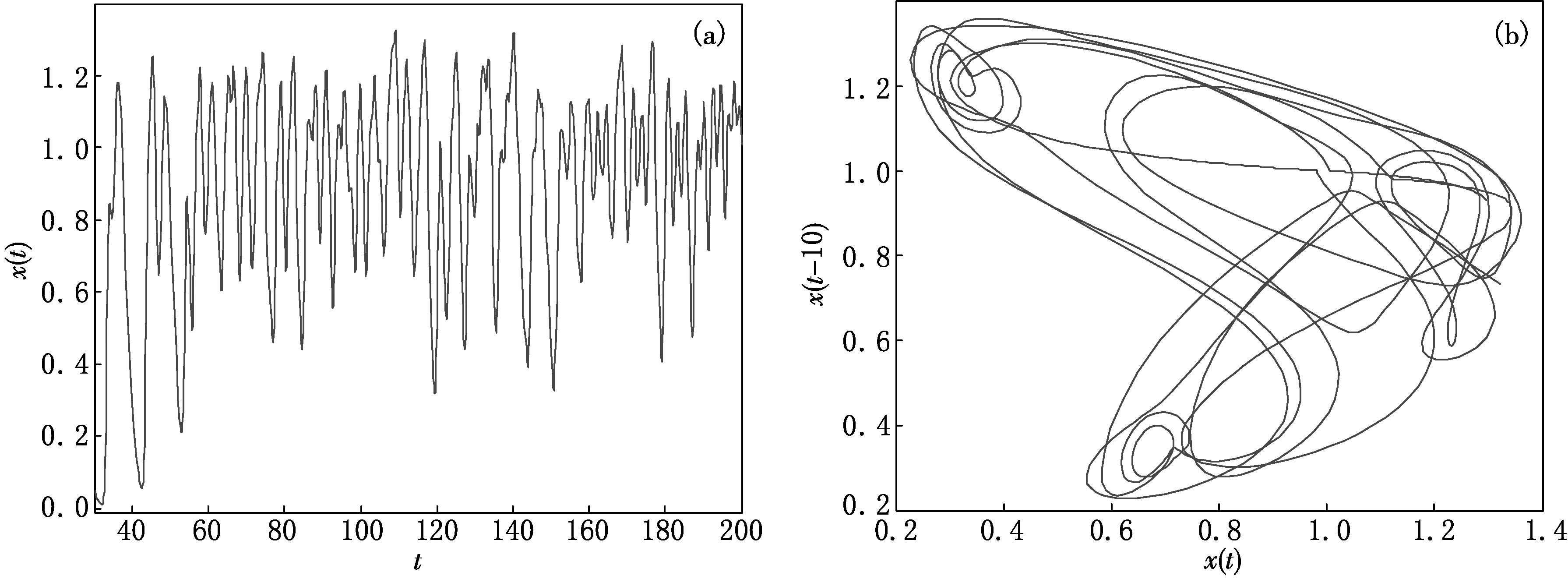
图2 当τ2=0,τ1=10时,系统(1)出现了混沌吸引子
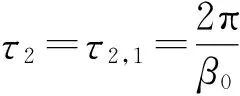
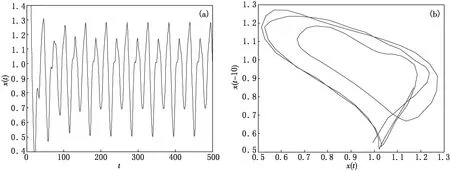
图3 当τ1=10,τ2=1.622 3,k=3时,系统(1)的平衡点x1附近出现了周期为2的周期解
4 结论
本文研究了时滞对Mackey-Glass系统动力学行为的影响和混沌的控制. 首先,时滞反馈控制方法不能使系统的零平衡点控制为稳定的. 对于非零平衡点,从对系统线性化方程的特征方程根的分布分析入手,分别研究了具有单时滞和双时滞系统的线性稳定性. 发现当系统中的时滞经过一系列临界值时,系统经历了Hopf分支. 其次,应用时滞反馈控制方法,选择合适的反馈增益和时滞使系统在不稳定非零平衡点附近出现周期轨. 最后,通过数值模拟验证了理论结果. 利用得到的基本定理,能很好地判断此类模型平衡点的渐近稳定性和周期轨的存在性.因此本文的研究结果具有一定的实际意义.
[1] 尹社会,张勇,张付臣,等. 基于Lorenz系统的强迫Lorenz混沌系统的动力学研究[J]. 东北师大学报(自然科学版),2014,46(1):42-47.
[2] 秦进. 一类三维混沌系统的动力学行为研究[J]. 东北师大学报(自然科学版),2015,47(1):48-52.
[3] MACKEY M C,GLASS L. Oscillation and chaos in physiological control system[J]. Science,1977,197:287-289.
[4] SHAHVERDIEV E M,NURIEV R A,HASHIMOV R H. Chaos synchronization between the Mackey-Glass systems with multiple time delays[J]. Chaos,Solitons and Fractals,2006,29:854-861.
[5] MACKEY M,HEIDEN U. Dynamic diseases and bifurcations in physiological control systems[J]. Funk Biol Med,1982(1):156-164.
[6] BEREZANSKV L,BRAVERMAN E,IDELS L. Mackey-Glass model of hematopoiesis with non-monotone feedback:stability,oscillation and contol[J]. Applied Mathematics and Computation,2013,219:6268-6283.
[7] 侯爱玉,彭震春. 离散时滞Mackey-Glass系统的稳定性与分岔[J]. 湖南工业大学学报,2010,24(5):23-27.
[8] PYRAGAS K. Synchronization of coupled time delay systems[J]. Analytical Estimations Phys Rev E,1998,58:3067-3071.
[9] RUAN S,WEI J. On the zeros of transcendental functions to stability of delay differential equations with two delays[J]. Dyn Contin Discrete Impuls Syst A Math Anal,2003,10:863-874.
[10] HALE J K,LUNEL S V. Introduction to functional differential equation[M]. New York:Springer-Verlag,1993:189-192.
[11] CAHLON B. On the stability of Volterra integral equations with a lagging argument[J]. BIT,1995,35:19-29.
(责任编辑:李亚军)
Stability and chaotic control of Mackey-Glass time-delayed system
YANG Ji-hua1,LI Yan-qiu2
(1.Department of Mathematics and Computer Science,Ningxia Normal University,Guyuan 756000,China;2. College of Science,Nanjing University of Technology,Nanjing 210009,China)
It is investigated that the effect of delay on dynamic behavior and chaotic control of Mackey-Glass system. Firstly,we show that delayed feedback control cannot stabilize the origin. For non-zero equilibrium,the linear stabilities with one delay and two delays are respectively investigated by analyzing the distribution of the roots of associated characteristic equation.It is found that Hopf bifurcations exist when the delays pass through a sequence of critical values. Secondly,applying of delayed feedback control method,by designing appropriate feedback strength and delay,we show that the unstable equilibrium can be controlled to be stable bifurcating periodic solutions at the neighborhood of the equilibrium. Finally,some numerical simulations are carried out for supporting the analytic results.
stability;Hopf bifurcation;chaotic attractor;chaotic control;period orbit
1000-1832(2015)04-0030-06
10.16163/j.cnki.22-1123/n.2015.04.007
2014-04-14
国家自然科学基金资助项目(11361046,11301263);宁夏自然科学基金资助项目(NZ13213);宁夏高等学校科研项目(GX2014[222]17).
杨纪华(1983—),男,讲师,主要从事微分方程的稳定性与分支研究.
O 175.13 [学科代码] 110·44
A

