关于Diophantine方程x3±1=6pqy2的整数解

杜 先 存

(红河学院教师教育学院，云南 蒙自 661199)

关于Diophantine方程x3±1=6pqy2的整数解

杜 先 存

(红河学院教师教育学院，云南 蒙自 661199)

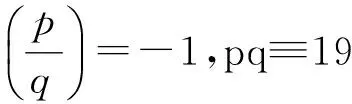
Diophantine方程；平方剩余；整数解；奇素数；递归序列；同余式

1 预备知识

方程

x3±1=Dy2(D>0，D无平方因子，x，y∈Z)

(1)

是一类重要而又基本的Diophantine方程，其整数解问题受到广泛的重视，目前已有众多结果：

(Ⅰ)D不含6k+1型的质因素时，已有结论如下：

(ⅰ)D不含质数3时，文献[1]证明了方程(1)只有平凡解；

(ⅱ)D含质数3时，文献[2]证明了方程(1)只有平凡解.

(Ⅱ)D含一个6k+1型的质因素时，已有结论如下：

(ⅰ)D含质数2时，文献[3]和文献[4]分别给出了方程x3-1=26y2，x3+1=38y2的全部整数解；

(ⅱ)D含质数3时，文献[5]给出了方程(1)仅有平凡解的两个充分条件；文献[6]和文献[7]分别给出了方程x3+1=57y2，x3+1=201y2的全部整数解.

(Ⅲ)D含两个不同的6k+1型的质因素时，方程(1)的整数解较为困难，目前的结论还不多见，已有结论如下：

(ⅰ)D不含质数2及质数3时，文献[8]和文献[9]分别给出了方程x3+1=91y2及x3±1=1 267y2的全部整数解；

(ⅱ)D含质数2或质数3时，关于方程(1)的整数解问题，目前还没有相关结论.

本文给出了D含质数2，质数3及两个互异的6k+1型的质因素时，方程(1)只有平凡解的充分条件.

引理1[10]设p是一个奇质数，则丢番图方程4x4-py2=1除p=3，x=y=1和p=7，x=2，y=3外，无其他的正整数解.

引理2[10]设p是一个奇质数，则丢番图方程x4-py2=1除p=5，x=3，y=4和p=29，x=99，y=1 820外，无其他的正整数解.

2 主要定理及证明

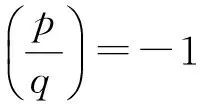
(ⅰ)p≡1(mod 24)，q≡13(mod 24)；

(ⅱ)p≡1(mod 24)，q≡19(mod 24)；

(ⅲ)p≡7(mod 24)，q≡13(mod 24).

则Diophantine方程

x3-1=6pqy2

(2)

只有平凡解(x，y)=(1，0).

证明 设(x，y)是方程(2)的正整数解，则x≡1(mod 3)，从而gcd(x-1，x2+x+1)=3.又x2+x+1≡0(mod 9)，x2+x+1≡0(mod 2)，故方程(2)给出下面4种可能的情形：

Ⅰx-1=18pqu2，x2+x+1=3v2，y=3uv，gcd(u，v)=1；

Ⅱx-1=18u2，x2+x+1=3pqv2，y=3uv，gcd(u，v)=1；

Ⅲx-1=18pu2，x2+x+1=3qv2，y=3uv，gcd(u，v)=1；

Ⅳx-1=18qu2，x2+x+1=3pv2，y=3uv，gcd(u，v)=1.

以下讨论这4种情形所给的方程(2)的整数解.

情形Ⅰ 将x=18pqu2+1代入x2+x+1=3v2，整理得

(2v)2-3(12pqu2+1)2=1.

(3)

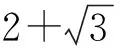
12pqu2=yn-1.

(4)

由(4)式得

yn≡1(mod 12).

容易验证下列各式成立：

yn+2=4yn+1-yn，y0=0，y1=1；

(5)

xn+2=4xn+1-xn，x0=1，x1=2；

(6)

x2n+1≡2(mod 3)，x2n≡1(mod 3)；

(7)

x2n+1≡2(mod 4)，x2n≡1(mod 2)；

(8)

y2n+1≡1(mod 2)，y2n≡0(mod 4).

(9)

对递归序列(5)取模12，得周期为12的剩余类序列，且仅当n≡-1(mod 12)，有yn≡-1(mod 12)；n≡1(mod 12)，有yn≡1(mod 12).所以只有n≡1(mod 12)时，(4)式才成立.

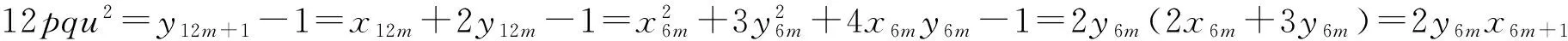
6pqu2=x6m+1y6m.

(10)

由(7)与(8)式得，x6m+1≡0(mod 3)，x6m+1≡2(mod 4).又gcd(x6m+1，y6m)=gcd(2x6m+3y6m，y6m)=gcd(2x6m，y6m)=gcd(2，y6m)=2，所以(10)式给出以下4种可能的情形：

(1)x6m+1=2a2，y6m=12pqb2，u=2ab，gcd(a，b)=1；

(2)x6m+1=2pqa2，y6m=12b2，u=2ab，gcd(a，b)=1；

(3)x6m+1=2qa2，y6m=12pb2，u=2ab，gcd(a，b)=1；

(4)x6m+1=2pa2，y6m=12qb2，u=2ab，gcd(a，b)=1.

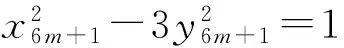
情形(2) 由y6m=12b2，x3my3m=6b2.又由(7)式，x3m≡0(mod 3)，而gcd(x3m，y3m)=1，故下列情形之一成立：

x3m=c2，y3m=6d2，b=cd，gcd(c，d)=1；

(11)

x3m=2c2，y3m=3d2，b=cd，gcd(c，d)=1.

(12)

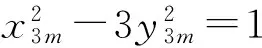
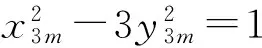
情形(3) 由y6m=12pb2得x3my3m=6pb2.又由(7)式得x3m≡0(mod 3)，而gcd(x3m，y3m)=1，故下列情形之一成立：

x3m=c2，y3m=6pd2，b=cd，gcd(c，d)=1；

(13)

x3m=2c2，y3m=3pd2，b=cd，gcd(c，d)=1；

(14)

x3m=pc2，y3m=6d2，b=cd，gcd(c，d)=1；

(15)

x3m=2pc2，y3m=3d2，b=cd，gcd(c，d)=1.

(16)

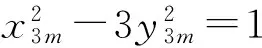
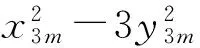
对于(15)式，将y3m=6d2两边取模8得

y3m≡6d2(mod 8).

(17)

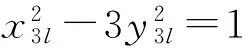
对于(16)式，将y3m=3d2两边取模8得

y3m≡3d2(mod 8).

(18)

因为x3m=2pc2，p为奇素数，故由(8)式知m为奇数，y3m≡1，7(mod 8).再由y3m=3d2及(9)式，d为奇数，即d2≡1(mod 8).所以(18)式为1，7≡3(mod 8)，矛盾，故该情形方程(2)无整数解.

情形(4) 仿情形(3)的证明可得方程(2)在该情形下也无整数解.

情形Ⅱ 由于u2≡0，1，4(mod 8)，利用同余的性质可得该情形不成立，故方程(2)在该情形下无整数解.

情形Ⅳ 由情形Ⅲ的证明再利用p，q的对称性可知方程(2)在该情形下也无整数解.

综上所述，定理1成立.

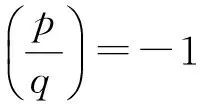
(ⅰ)p≡1(mod 24)，q≡13(mod 24)；

(ⅱ)p≡7(mod 24)，q≡1(mod 24)；

(ⅲ)p≡19(mod 24)，q≡13(mod 24).

Diophantine方程

x3+1=6pqy2

(19)

只有平凡解(x，y)=(-1，0).

证明 事实上，仿定理1的证明可知方程(19)给出下面4种可能的情形：

Ⅰx+1=18pqu2，x2-x+1=3v2，y=3uv，gcd(u，v)=1；

Ⅱx+1=18u2，x2-x+1=3pqv2，y=3uv，gcd(u，v)=1；

Ⅲx+1=18pu2，x2-x+1=3qv2，y=3uv，gcd(u，v)=1；

Ⅳx+1=18qu2，x2-x+1=3pv2，y=3uv，gcd(u，v)=1.

情形Ⅰ 将x=18pqu2-1代入x2-x+1=3v2，整理得

(2v)2-3(12pqu2-1)2=1.

(20)

仿照定理1的证明可知方程(20)的一切整数解为

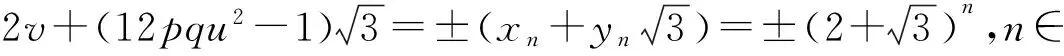
为此也只需考虑方程

12pqu2=yn+1.

(21)

由(21)式，yn≡-1(mod 12).因为仅当n≡-1(mod 12)时，有yn≡-1(mod 12)，所以只有当n≡-1(mod 12)时，(21)式才成立.

当n≡-1(mod 12)时，不妨设n=12m-1(m∈Z)，仿定理1的证明可知(21)式可化为

6pqu2=x6m-1y6m.

(22)

由(5)式知，仅当m=0时，y6m=0.又由(6)式知对于任意整数m，均有x6m-1≠0，所以仅当m=0时，x6m-1y6m=0.

m=0时，由(22)式得u=0，此时得出方程(19)的平凡解(x，y)=(-1，0).

m≠0时，仿定理1的(10)式证明可知方程(22)无整数解，故方程(19)在该情形下无整数解.

情形Ⅱ 由于u2≡0，1，4(mod 8)，利用同余的性质可得该情形不成立，故该情形方程(19)无整数解.

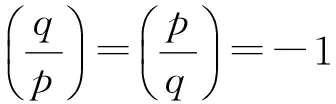
情形Ⅳ 由情形Ⅲ的证明再利用p，q的对称性可知方程(19)也无整数解.

综上所述，定理2成立.

[1] 柯召，孙琦.关于丢番图方程x3±1=Dy2[J].中国科学，1981，24(12)：1453-1457.

[2] 柯召，孙琦.关于丢番图方程x3±1=3Dy2[J].四川大学学报(自然科学版)，1981，18(2)：1-5.

[3] 罗明，黄勇庆.关于不定方程x3-1=26y2[J].西南大学学报(自然科学版)，2007，29(6)：5-7.

[4] 段辉明. 关于不定方程x3+1=38y2[J].华东师范大学学报(自然科学版)，2006，1：35-39.

[5] 杜先存，吴丛博，赵金娥.关于Diophantine方程x3±1=3Dy2[J].沈阳大学学报(自然科学版)，2013，25(1)：84-86.

[6] 段辉明.关于不定方程x3+1=57y2[J].重庆师范大学学报(自然科学版)，2010，27(3)：41-43，72.

[7] 李双志，罗明.关于不定方程x3+1=201y2[J].西南师范大学学报(自然科学版)，2010，35(1)：11-14.

[8] 杜先存，管训贵，杨慧章.关于不定方程x3+1=91y2[J].内蒙古师范大学学报(自然科学汉文版)，2013，42(4)：397-399.

[9] 杜先存，万飞，杨慧章.关于丢番图方程x3±1=1267y2的整数解[J].数学的实践与认识，2013，43(15)：288-292.

[10] 曹珍富.丢番图方程引论[M].哈尔滨：哈尔滨工业大学出版社，2012：180，187.

(责任编辑：李亚军)

On integer solutions of the Diophantine equationx3±1=6pqy2

DU Xian-cun

(College of Teacher Education，Honghe University，Mengzi 661199，China)

Diophantineequation；quadraticremainder；integersolution；oddprime；congruence；recursivesequence

1000-1832(2015)04-0026-04

10.16163/j.cnki.22-1123/n.2015.04.006

2014-02-07

国家自然科学基金资助项目(11371291)；云南省教育厅科研基金资助项目(2014Y462)；喀什师范学院校级课题((14)2513).

杜先存(1981—)，女，硕士，副教授，主要从事初等数论研究.

O

A