基于跳数修正的DV-Hop改进算法*

夏少波,朱晓丽,邹建梅,连丽君

(山东广播电视大学计算机与通信学院,济南 250014)



基于跳数修正的DV-Hop改进算法*

夏少波*,朱晓丽,邹建梅,连丽君

(山东广播电视大学计算机与通信学院,济南 250014)

针对无线传感器网络DV-Hop定位算法在实际应用中定位误差较大的问题,提出一种基于跳数修正的改进算法。在引入限跳机制的条件下,按未知节点与信标节点间的跳数值分类估算,对1跳区域内的节点采用RSSI测距技术,对于节点间跳数值大于1跳的节点,则利用信标节点间实际距离与估计距离的误差值修正平均每跳距离。仿真实验表明,在相同的网络条件下,与原DV-Hop定位算法和其他改进算法相比,改进后的算法能更有效地减少跳距估算带来的定位误差,提高平均定位精度并保持较好的算法稳定性。

无线传感器网络;节点定位;定位误差;限跳机制;平均跳距

无线传感器网络WSN(Wireless Sensor Network)是由大量智能传感器节点构成的集信息采集、传送和处理为一体的综合智能信息网络,具有环境适应性强、自组织能力和组网成本低等特点[1]。网络节点协作感知、采集和处理覆盖区域内被检测对象的信息,并将结果传送给观测者。WSN在目标跟踪、环境监测甚至是军事侦测等众多的领域都有广泛的应用,引起了学术界的广泛关注和深入研究[2]。对大多数WSN应用而言,没有时空标识的数据和信息是没有意义的,因此,节点的准确定位在传感器网络的应用中起关键作用[3-4]。目前研究者已经提出了很多节点定位算法。按定位所采用的节点间距离获取方式,一般把定位算法分为基于测距算法(Range-based)和无需测距算法(Range-free)两大类[5-7],前者主要有RSSI(Received Signal Strength Indicator)、TDOA(Time Difference on Arrival)、AOA(Angle of Arrival)和TOA(Time of Arrival)等。后者主要有DV-Hop(Distance Vector-Hop)、凸规划定位、质心定位、MDS-MAP定位、Amor-phous定位和APIT(Approximate PIT Test)定位等。上述众多算法各有其优势和不足,第1类方法采用测距技术,通常精度较高,但需要附加硬件设备而且测距效果受环境影响较大[8];第2类方法虽然精度稍低,但因其成本低廉,受环境影响较小等优点,越来越受到关注。尤其是DV-Hop节点定位算法,以其经济性和简单实效性得到了广泛应用,但DV-Hop定位算法的缺点是定位误差稍高[9]。本文深入分析了DV-Hop定位算法存在的缺陷,在不改变原算法步骤,少量增加硬件设备的条件下,提出了一种基于跳数修正的DV-Hop改进算法。

1 传统DV-Hop算法及其存在的不足

DV-Hop属于距离矢量路由DVR(Distance Vector Rou-ting)和全球定位系统GPS(Global Positioning System)技术综合应用产生的一组分布式定位算法——自组织定位算法APS(Ad-hoc Positioning System),是由美国路特葛斯大学的Dragos Niculescu等人早年提出的[10]。该算法的优点是具有较高的定位覆盖率、易于扩展、廉价和受限条件少等,因其定位精度能满足大多数WSN应用的需要,而被广泛地应用和研究。

1.1 传统DV-Hop算法描述

传统DV-Hop节点定位算法分为以下3个步骤[11-12]:

①网络中的信标节点利用典型的距离矢量路由协议,在网络中广播包含自身位置信息的数据分组(含有位置和跳数字段等信息,跳数初始值设为零),网络中的相邻节点作为接收方,记录至各信标节点间的最小跳数,并抛弃来自同一信标节点的较大跳数分组。再将跳数值加1后转发出去。反复此步骤,各节点均记录下至各信标节点间的最小跳数值。

②每个信标节点在获得其他信标节点的位置坐标和最小跳数值后,计算各自的平均每跳距离,然后将其作为校正值以洪泛的方式广播至网络中。信标节点i的平均每跳距离(校正值)的估算公式如式(1)。

(1)

式中:(xi,yi),(xj,yj)分别表示信标节点i和j的坐标,hj表示信标节点i与j之间的跳数值。

(2)

③未知节点利用第2阶段操作估算出的到3个(或以上)信标节点间的跳距,最后再采用三边测量法或极大似然法估算自己的坐标值。

图1是传统DV-Hop定位算法总流程。

图1 DV-Hop定位算法流程

相关研究表明,在网络节点平均连通度为10,信标节点占比为10%,且各向同性的环境中,DV-Hop的平均定位精度可以达到33%左右[4],可见对于节点分布均匀、且密集型的网络,该算法的定位精度基本能满足要求。但在实际应用中,网络的拓扑结构常常是随机且不规则的,如果直接使用DV-Hop算法,定位精度就会迅速下降。

1.2 DV-Hop算法误差原因分析

①实际应用中,节点是随机播撒在检测区域内,网络的拓扑结构是不规则的,且节点分布不可能均匀,这必然造成网络中不同区域内节点密度差别较大[13],从而使不同区域内的节点接收到的与各信标节点间的最小跳数值存在一定偏差,且随着跳数值的增大,该偏差也将累计加大,导致测距误差变大,影响定位精度。

②通信范围内能相互直接通信的节点互称为邻居节点,又称之为1跳(1h)区域节点,图2所示为节点x的1跳区域示意图。

图2 节点的1跳区域示意图

图2中,假设方形点I、J代表信标节点,标号为1、2、3、…、x的圆形点代表未知节点,用r代表节点的通信半径,则图中所示以r为半径的圆形区域内,就是节点x的1跳区域。图2可看出,圆圈内的节点尽管都是x的1跳节点,但有的靠近圆心处(如节点1),而有的则靠近虚线圆圈内侧(如节点4),它们距处于圆心的节点x的实际距离相差较大,然而DV-Hop算法的规则是:1跳区域内的所有节点的间距,一律按统一的1跳距离估值。这势必造成较大误差。

③DV-Hop算法的核心思想是用接收到的最近信标节点的平均每跳距离与跳数值的乘积估算未知节点与信标节点之间的距离,即使用跳段距离代替直线距离。这对于各向同性的密集网络,可以得到合理的平均每跳距离,达到适当的测距精度[14],但对于拓扑不规则的网络,由于节点分布不可能均匀,必将存在以下两方面的缺陷:一是用单个信标节点估算的平均每跳距离值无法准确地反映全网络各区域的实际平均每跳距离,采用相同的平均每跳距离估算,就造成了未知节点与其他信标节点间的测距精度降低[8];二是节点间大多是折线连接,节点密度越小折线率越高,因此当网络中未知节点和信标节点之间的跳数值大于1跳时,以折线结构的跳段距离近似代替直线距离,平均每跳距离的估算值与实际值误差就会加大,导致DV-Hop算法的估算距离与实际距离间存在较大的误差,且误差与节点间的跳数值成正比[7]。以下,用图3所示的节点分布为例,做进一步的说明。

图3 节点分布示意图

在图3所示节点分布图中,中间处的方形节点I代表信标节点,其他所有标号为1、2、3、…12等圆形节点代表未知节点,图中以中间为界左边1、2、3、…5等节点较密集,而右边6、7、8、…12等节点分布较稀疏,图中的若干虚线圆圈代表几个节点的通信范围。由图不难看出,尽管信标节点I到未知节点5与信标节点I到未知节点12之间的距离大致相同(图中两条虚直线),但由于左边节点分布较密集,I到节点5之间有多种跳段路径可供选择,且折线近似直线;而右边节点分布较稀疏,I到节点12之间可供选择的路径较少,且折线率高,这就造成I到节点5间的跳数值是3跳,而I到节点12间的跳数值是4跳。这种情况下,节点5和12若再采用相同的平均每跳距离去估算,就会导致测距估算误差过高。

2 改进策略分析

2.1 已有的改进策略分析

针对传统DV-Hop算法存在的不足,文献[5]对算法的改进策略是:利用无线信号在同种介质中传播速度的不变性,用计数器来测量信标节点间的传送时间以及信标节点与未知节点间的传送时间,再利用该时间比例修正未知节点的估算距离,以达到降低距离估算误差的目的。文献[7]对算法的改进策略是:从半自动获取平均每跳距离、划分定位区域到对边缘区域采用坐标贴边等3个方面进行了改进,所谓“半自动”是指在获取平均每跳距离的过程中,并不是每个步骤都由节点自动完成,而需要人工的参与,事先靠人工在节点中手动写入必要的参数,这种改进策略虽能提升定位精度,但需要人工参与就会影响WSN的应用范围。文献[8]对算法的改进策略是从如下两个方面进行,一是信标节点首先计算出实际距离与估算距离间的误差,再用该误差作为修正值修正信标节点的平均每跳距离。二是摒弃了传统的三边定位算法而采用新的二维双曲线定位算法估算未知节点的坐标。本文在文献[8]改进算法的基础上,以节点间的跳数值为突破口,引入限跳机制,按未知节点与信标节点间的跳数值不同进行分类估算,对于1跳区域内的节点,直接采用RSSI测距技术完成测距,而对于跳数值大于1跳的节点,则用节点间实际距离与估算距离的误差值对平均每跳距离进行重新修正。

2.2 本文改进策略描述

针对传统DV-Hop定位算法存在的上述诸如跳数值越大则累计误差就越高,1跳区域内节点距离估算不合理,平均每跳距离误差过大等缺陷,本文提出了如下3方面的改进策略。

2.2.1 策略1:引入限跳机制

鉴于节点间的跳数值越大,距离估算误差越高的缺陷,本文在改进算法中引入限跳机制,即设置一个阈值N(跳数值上限)。具体操作是:信标节点向网络中广播包含自身位置信息的分组时,在分组中再附加参数N,称之为跳数阈值,网络中邻居节点接收到该分组后,首先比较跳数h与阈值N的大小,如果h小于N,则h=h+1,并转发该分组,否则丢弃此分组不再转发,这样就可以保证每个节点只接收N跳范围内信标节点的位置信息。

跳数阈值N的大小主要依据网络的连通度和节点密度确定[15],如式(3)所示。

(3)

式中:r表示节点的通信半径,A表示网络内所有节点总数,ρ表示信标节点占比,L表示整个检测正方形区域的边长,M表示定位未知节点所需要的最小信标节点的个数。为提高节点定位率和定位精度,通常N的取值要比理论估算值稍大一点(一般取3或4),以满足网络整体的定位覆盖率。

2.2.2 策略2:引入RSSI测距技术

随着微电子和通信技术的高速发展,RSSI测距技术也实现了低成本和高效能。实际应用中,适当将基于测距(Range Based)和无需测距(Range Free)技术综合应用,会收到取长补短的效果。通常只需给传感器节点增加小许硬件开销,即可实现精度较高的RSSI短距离(邻居节点间)测距。在DV-Hop算法的第2步,节点接收到其他节点位置信息后,在进行节点间跳距估算之前,先对节点间的跳数值做一个判断,若节点间的跳数值是1跳,则直接采用RSSI测距技术,若节点间的跳数值大于1跳,则按策略3(后述)估算跳距。

RSSI主要使用RF(射频)信号测距,由于无线信号在传播过程中,信号的功率强度会衰减,也就是:已知发射节点的发射信号强度,根据接收节点接收的信号强度,依据信号功率衰减速率与距离的关系进行测距,利用理论的或经验的信号传播模型将传播损耗转化为距离。常用的路径损耗模型有:自由空间传播、对数距离路径损耗、对数常态分布等,本文选择RSSI在WIN应用较多的对数常态分布模型[3]。其表达式如下所示。

Pr(d)=Pr(d0)+10nlg(d/d0)+Xσ

(4)

式中:d代表两节点间的距离,d0代表参考距离,Pr(d)代表距离发射处dm接收到的信号功率强度,Pr(d0)代表距离发射处d0m接收到的信号功率强度,n代表信道衰减指数,Xσ代表均值为0、标准差为σ的高斯分布。实际计算中,通常d0取1 m,Pr(d0)也是取1 m处的信号功率强度。对于芯片CC2430,有以下关系成立。

RSSI=Pr(d)+RSSI_OFFEST

(5)

借助上述公式,可以推导出式(6)

PR(dBm)=A+10nlgr+Xσ

(6)

式中:A=Pr(1)+RSSI_OFFEST。系数A和n可以通过数据采集拟合得到。

2.2.3 策略3:修正参与定位的各信标节点的平均每跳距离

这是针对传统算法第2步操作进行的改进,原算法是采用节点间的跳数值与接收到最近信标节点的平均每跳距离的乘积估算未知节点到各信标节点间的距离,用折线跳段距离代替直线距离。由于网络拓扑结构是不规则的,且节点分布不可能均匀,局部区域内节点密度越低折线率越高,误差就会越大。因此,当平均每跳距离的估算值与实际值相差较大时,未知节点到信标节点的估算距离与两者间实际距离的误差就会加大[8]。本文采用与传统算法相似的步骤估算平均每跳距离,不同之处在于,信标节点还要估算出实际距离与估算距离间的误差,再用该误差作为修正值修正信标节点的平均每跳距离,最后将修正后的平均每跳距离作为校正值向外广播,操作原理如下:

假设(xi,yi),(xj,yj)分别表示信标节点i和j的坐标,hij表示信标节点i与j之间的跳数值。Di,j表示信标节点i和j之间的实际距离,则有:

(7)

(8)

假设用Ei,j表示信标节点i与信标节点j之间的距离总估算误差,则有:

(9)

(10)

则信标节点i与信标节点j之间修正之后的平均每跳距离为:

(11)

每个信标节点将修正后的平均每跳距离作为校正值发送到网络中。通过这一步改进,能大大降低由于网络局部区域内节点分布不均匀而带来的距离估算误差。

综合上述3方面的改进策略,得出本文改进算法的节点操作流程,图4是信标节点i的流程,图5是未知节点节点x的流程。

图4 改进后信标节点i的操作流程

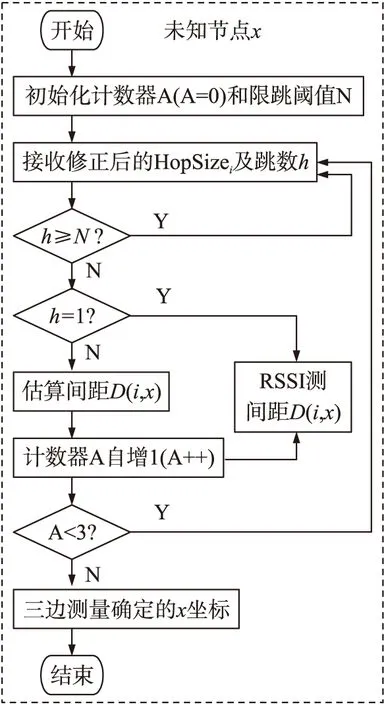
图5 改进后未知节点x的操作流程

3 仿真测试与结果分析

为评估本文改进算法的有效性,利用MATLAB7.10分别对传统的DV-Hop算法、文献[5]、文献[8]改进算法及本文算法进行仿真实验,并对实验数据分析比较。为了取得更客观、更准确的实验数据,全部数据采用100次相同实验的平均值。所有实验均为二维随机分布,尽量保证节点的分布具有一定的均匀性,实验区域大小设定为100m×100m的正方形区域,信标节点与未知节点的通信半径r相同,本文改进算法限跳阈值N取4,由于本研究尚没有明确实用环境(不确定),式(6)中的参数A和n无法事先预知,本文算法中各节点均采用经验数据,预设A=-40dBm,n=3,采用对数常态分布模型对1跳节点进行RSSI测距。

图6所示是节点密度与定位误差率的关系,检测区域内通过改变节点的总数来改变平均网络节点密度,设置信标节点占比恒定为10%,节点的通讯半径r为20m不变,调整节点总数从100逐步递增到180(每次增加10个)。通过对传统的DV-Hop算法、文献[5]、文献[8]改进算法以及本文算法进行实验数据对比,图6可以明显看出,随着节点总数的增加,平均网络节点密度逐步提高,4种算法的定位误差率都得到了改善,且在相同节点数的情况下,本文算法的定位误差率明显优于传统算法及其他两种改进算法。总体看,本文算法比传统DV-Hop算法的定位误差率减少了约17%,与文献[5]、文献[8]相比减少了约5%。

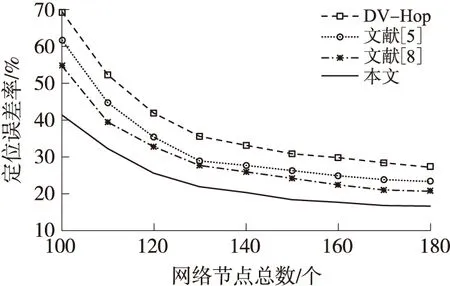
图6 节点密度对平均定位误差率的影响

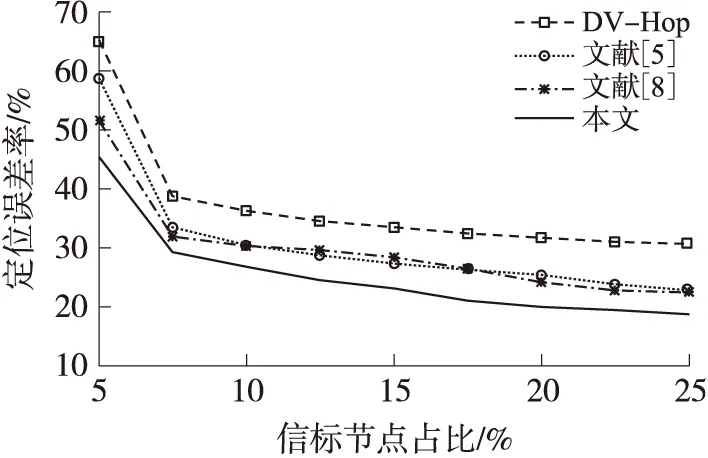
图7 信标节点占比对定位误差率的影响

图7为信标点占比与定位误差率的关系,在检测区域内节点总数量固定为160个,通信半径r=20m不变,调整信标节点占比从5%递增到25%(每次增加5%)。仿真实验图7可以看出,上述4种算法都呈现随着信标节点占比的增加,定位误差率逐渐降低的趋势,当信标节点占比为10%左右时,4种算法定位误差率降低较快,而当信标节点占比达到20%以后,定位误差率降低幅度趋缓。且本文算法比传统DV-Hop算法以及文献[5]和文献[8]两种改进算法定位更精确。总体看,本文算法比传统DV-Hop算法的定位误差率减少了约15%,比文献[5]和文献[8]减少了约4%。

图8为节点通信半径r与定位误差率的关系,在检测区域内设置节点总数量恒定为160个,信标节点占比为10%不变,调整节点的通信半径r从15m逐渐递增到35m(每次增加5m)。图8可以看出,4种算法定位误差率都是随着节点通信半径r的递增而下降。数据显示,本文算法比传统DV-Hop算法的平均定位误差率减少了约16%,与文献[5]、文献[8]相比减少了约5%。

图8 节点通信半径r对定位误差率的影响

4 结论

传统的DV-Hop算法用接收的最近信标节点的平均每跳距离乘以跳数值估算节点间的距离。本文在不改变传统DV-Hop算法步骤的基础上,提出一种基于跳数值修正的改进算法。仿真测试表明,在相同的网络环境下,与传统算法和其他改进算法想比,本文算法能更有效地降低距离估算误差,提高节点的定位精度。但本文算法也有以下不足:一是为了增加定位的精确性,引入了RSSI测距技术,导致节点硬件开销比传统算法略有增大,二是对信标节点的平均每跳距离重新修正,也带来了计算量稍有增加,但随着微电子技术的高速发展,这些不足应该不成问题。在具体使用中,可以结合传统DV-Hop算法、其他改进算法和本文算法综合加以应用。

[1] 孙利民,李建中,陈渝,等. 无线传感器网络[M]. 北京:清华大学出版社,2005:135-155.

[2]Nicolescu D,Nath B. DV Based Positioning in Ad Hoc Networks[J]. Journal of Telecommunication Systems,2003,22(1/4):267-280.

[3]金纯,叶诚,韩志斌,等. 无线传感器网络中DV-Hop定位算法的改进[J]. 计算机工程与设计,2013,34(2):401-404.

[4]Ren F Y,Huang H N,Lin C. Wireless Sensor Network[J]. Journal of Software,2003,4(7):1282-1291.

[5]赵灵锴,洪志全. 基于无线传感器网络的DV-Hop定位算法的改进[J]. 计算机应用,2011,31(5):1189-1192.

[6]Nagpal R,Shrobc H,Bachrach J. Organizing a Global Coordinate System from Local Information on an Ad Hoc Sensor Network[C]//Proc of IPSN’03. Berlin:Springer-Verlag,2003:333-348.

[7]毛科技,赵小敏,何文秀,等. WSN中基于区域划分的半自动DV-Hop定位算法[J]. 计算机科学,2012,39(3):39-42.

[8]石为人,贾传江,梁焕焕. 一种改进的无线传感器网络DV-HOP定位算法[J]. 传感技术学报,2011,24(1):83-87.

[9]Jonathan B,Christopher T. Handbook of sensor networks[C]//Stojm Enovic Ⅱ,ed. Proc of Localization in Sensor Networks,2005:1-18.

[10]Niculescu D,Nath B. Ad hoc Positioning System(APS)Using AOA[C]//Infocom 2003. 22nd Annual Joint Conference of the IEEE Computer and Communications. San Francisco,USA:2003,IEEE Societies(3):1734-1743.

[11]李牧东,熊伟,梁青. 基于人工蜂群改进的无线传感器网络定位算法[J]. 传感技术学报,2013,26(2):241-245.

[12]Demirkol I,Ersoy C,Alagoz F. MAC Protocols for Wireless Sensor Networks A Survey[J]. IEEE Communications Magazine,2006,44(4):115-121.

[13]李辉,熊盛武,刘毅,等. 无线传感器网络DV-HOP定位算法的改进[J]. 传感技术学报,2011,24(12):1782-1786.

[14]Basagni S,Carosi A,Melachrinoudis E,et al. Protocols and Model for Sink Mobility in Wireless Sensor Networks[J]. ACM Sigmo-Bile Mobile Computing and Communications Review,2006(10):28-30.

[15]刘玉锟,廖惜春,沈海燕,等. 无线传感器网络中DV-HOP定位算法的改进[J]. 五邑大学学报,2013,27(2):59-64.

The Improved DV-Hop Algorithm Based on Hop Count*

XIAShaobo*,ZHUXiaoli,ZOUJianmei,LIANLijun

(College of Computer and Correspondence,Shandong TV University,Jinan 250014,China)

The DV-Hop positioning algorithm for wireless sensor network has lager error in its practical application. The paper put forward an improved algorithm which based on the modified hop count to solve it. Under condition of using the hop-limitation mechanism,according to the hop mechanism of the unknown nodes and beacon nodes to classify and estimate. For the nodes which on the 1 hop region using RSSI ranging technology,and the others use the error of beacon nodes actual distance and its estimated distance to fix the average hop distance. The simulation tests show that under the same network conditions,compared with the original DV-Hop algorithm and other improved algorithm,this improved algorithm can effectively reduce the positioning error of the hop distance estimation,improve the average positioning accuracy and keep its stability.

wireless sensor network;node localization;the positioning error;hop-limitation mechanism;the average hop distance

夏少波(1964-),男,山东烟台人,山东工业大学工学学士毕业,山东广播电视大学计算机与通信学院教授,主要研究方向为无线传感器网络、宽带无线接入技术等,xia_shaobo64@aliyun.com;

朱晓丽(1980-),女,山东临沂人,山东师范大学计算机科学与技术专业硕士毕业,山东广播电视大学计算机与通信学院副教授,主要研究方向为信息处理,网络安全等,sdnuzxl@163.com;

邹建梅(1979-),女,山东临沂人,曲阜师范大学教育学硕士毕业,山东广播电视大学计算机与通信学院副教授,主要研究方向为网络与计算机通信、计算机支持的协同工作、云计算等,zjm1979@163.com。

项目来源:山东省自然科学基金面上项目(ZR2012FM033)

2014-11-16 修改日期:2015-01-27

C:6150P

10.3969/j.issn.1004-1699.2015.05.024

TP393

A

1004-1699(2015)05-0757-06