可调分辨率的水下传感器网络压缩感知重构算法*
赵文强,胡 滨,康文静,刘功亮
(哈尔滨工业大学威海校区信息与电气工程学院,山东 威海 264209)
可调分辨率的水下传感器网络压缩感知重构算法*
赵文强,胡 滨,康文静*,刘功亮
(哈尔滨工业大学威海校区信息与电气工程学院,山东 威海 264209)
针对水下传感器网络信息获取过程的特点和压缩感知精确重构原始信号的限制条件,提出一种可调分辨率的水下传感器网络压缩感知重构算法。Sink节点根据获取到的随机观测向量的维度以及给定的分辨率调整策略,计算出重构分辨率,并根据重构分辨率及获取到的节点数据的位置信息处理随机观测向量,构造观测矩阵,最后,采用压缩感知重构算法重构待观测区域的原始物理信息。仿真结果表明,当节点的感知概率较小时,相比于固定分辨率的重构方案,可调分辨率的重构方案能显著提高重构精度。
水下传感器网络;压缩感知;重构精度;重构分辨率
近年来,对于水下传感器网络方面的研究越来越受到人们的关注。然而,相比于陆地通信环境,水下通信环境更加复杂,更加恶劣[1]。水下严重的电磁波衰减,使得通信只能采用频率,速度都比较低的声波。相比于电磁波,采用声波带来了更大的传播时延。相对于陆地通信,较低的通信频段使得通信带宽受到了更加苛刻的限制。水下通信节点的能量一般是通过电池供给,而水下电池很难被更换,所以,水下传感器网络的能量受到了限制。此外,复杂多变的水下信道环境使得水下通信拥有更高的数据传输误码率。
如何针对水下传感器网络的限制因素提出有效的解决方案,建立一个通信质量更高,寿命更长的传感器网络成为对于水下传感器网络研究的重点。压缩感知技术CS(Compressed Sensing)[2]作为一种新的高效的信息获取方式,在满足一定的条件下,通过得到一个稀疏信号的少量的随机的观测值,就能够高精度的恢复出原始信号。压缩感知技术已经在通信和信号处理中获得了大量的理论应用[3-5]。水下传感器网络采集到的测量数据具有时间和空间相关性,在傅立叶变换域,离散余弦变换域,小波变换域等变换域中表现为稀疏性[6]。所以,压缩感知技术为传感器网络信息获取方式提供了一种新思路。研究者们提出了一些将压缩感知理论应用于传感器网络的方案,并证明了两者结合能有效的降低传感器网络的能耗,节省传感器网络的带宽。针对传感器网络中的观测数据的空间相关性,文献[7]提出了一种随机接入方案,传感器节点以一定的接入概率被激活并发送数据。接收节点只是简单的丢弃掉碰撞的数据包,即便如此,接收节点也能够采用压缩感知技术以较高的重构精度重构出原始数据。相对于传统的接入方案,该方案能够节省带宽,降低能耗。文献[8]利用传感器网络测量数据的空间和时间相关性,从三个层面利用压缩感知技术实现信息的获取。在他们的方案中,传感器节点发送的数据包中不需要含有身份信息,进一步降低了系统的能耗,并且提高了系统的安全性。
压缩感知理论表明只要随机观测值的数目大于Ns=CSlogN,就能够以较高的概率唯一的恢复出原始信号。其中,N为原始信号的维度,S为原始信号的稀疏度,C为与N、S无关的常量[9]。然而,在实际的水下通信过程中,当信道质量较差时,误码率会较高,甚至会出现数据包的丢失;如果采用随机的接入方式,可能会发生数据包的碰撞,这些因素可能最终会导致Sink节点成功获取到的观测值数目小于Ns,重构精度降低,以至于不能达到系统的精度要求。
针对上一段中提出的压缩感知和传感器网络两者结合的过程中可能出现的问题,本文提出了一种根据Sink节点成功获取到的随机观测值的数目K,动态的调节重构分辨率的方案。文章中的重构分辨率是指对观测区域的物理信息重构的数据的个数。仿真结果表明,使用可调分辨率的压缩感知重构方案,在一定程度上保证了重构精度。
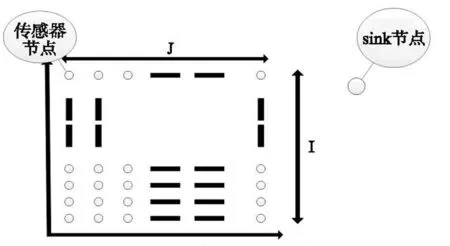
图1 传感器网络场景
1 系统模型
考虑这样一个传感器网络如图1所示,网络由N个普通传感器节点和一个Sink节点构成,且所有的普通传感器节点位于同一个水平面内。其中,N=IJ,J为沿x方向上的传感器节点个数,I为沿y方向上的传感器节点个数。普通传感器节点和Sink节点之间进行单跳通信。待观测的水下的物理信息是时变的,假设待观测的水下的物理信息的相关时间为Tcoh,即在Tcoh时间段内,待观测的水下的物理信息基本保持不变。为了保证Sink节点获取到的信息的有效性,一个数据帧的时间长度T应满足T≤Tcoh。在每一个数据帧的开始时刻,传感器节点i进行贝努力试验来确定是否参与数据传输。假设每个传感器节点参与数据传输的概率为p,保持休眠状态的概率为1-p。如果传感器节点i参与数据传输,那么传感器节点i选择一个随机发送延迟时间θi,其中θi在[0,T-Tp-τmax]上均匀分布。假设传感器节点发送的数据包长度为Lbit,系统带宽为B,一个数据包的时间长度Tp=L/B。传感器节点i和Sink节点之间的距离为Di,声速为c,那么最大的网络传播时延τmax=maxi∈{1,…,N}{Di/c}。根据压缩感知理论,Sink节点成功获取到的随机观测值的数目K大于等于Ns,就能以较高精度重构出整个观测区域的待观测物理信息。K大于等于Ns的概率为系统充分感知概率,记作Ps。对于由于发生数据包的碰撞或者信道质量较差导致的无法正确译码的数据包,Sink节点简单的丢弃掉。Sink节点通过解调,解码,最终在第n帧结束时获取到观测区域的待观测物理信息向量Y(n)。
Y(n)=Φ(n)X(n)+ε
(1)
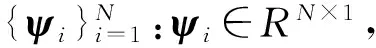
X(n)=ΨZ(n)
(2)
(3)
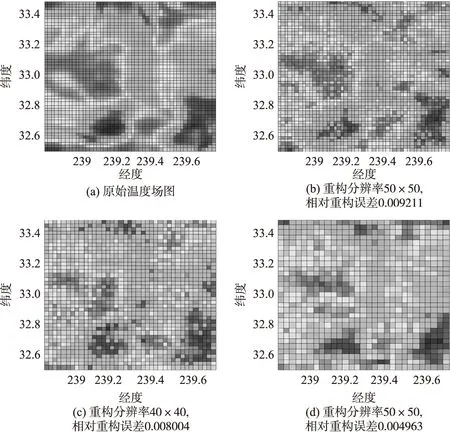
采用在2012年5月16号格林尼治时间,南加州海岸纬度[32.50,33.48],经度[238.80,239.78]地区测量得到的温度数值(数据来源于http://ourocean.jpl.nasa.gov)作为原始数据,N=50×50,离散余弦变换基DCT(Discrete Cosine Transform)为稀疏基,随机单位抽取矩阵为随机观测矩阵。并且假设一个数据帧的时间长度T=1 000,一个数据包的时间长度Tp=0.2。在系统充分感知概率Ps=0.9的条件下,根据文献[7]中的理论,并通过数值仿真计算出每个节点参与数据传输的概率为p=0.250 25。仿真结果如图2、图3所示。其中,相对重构误差为0.011 021;在图3中,黑色区域代表被成功随机观测到的区域。结果表明,采用上文的数据采集模型能够实现对传感器网络测量数据的压缩感知。
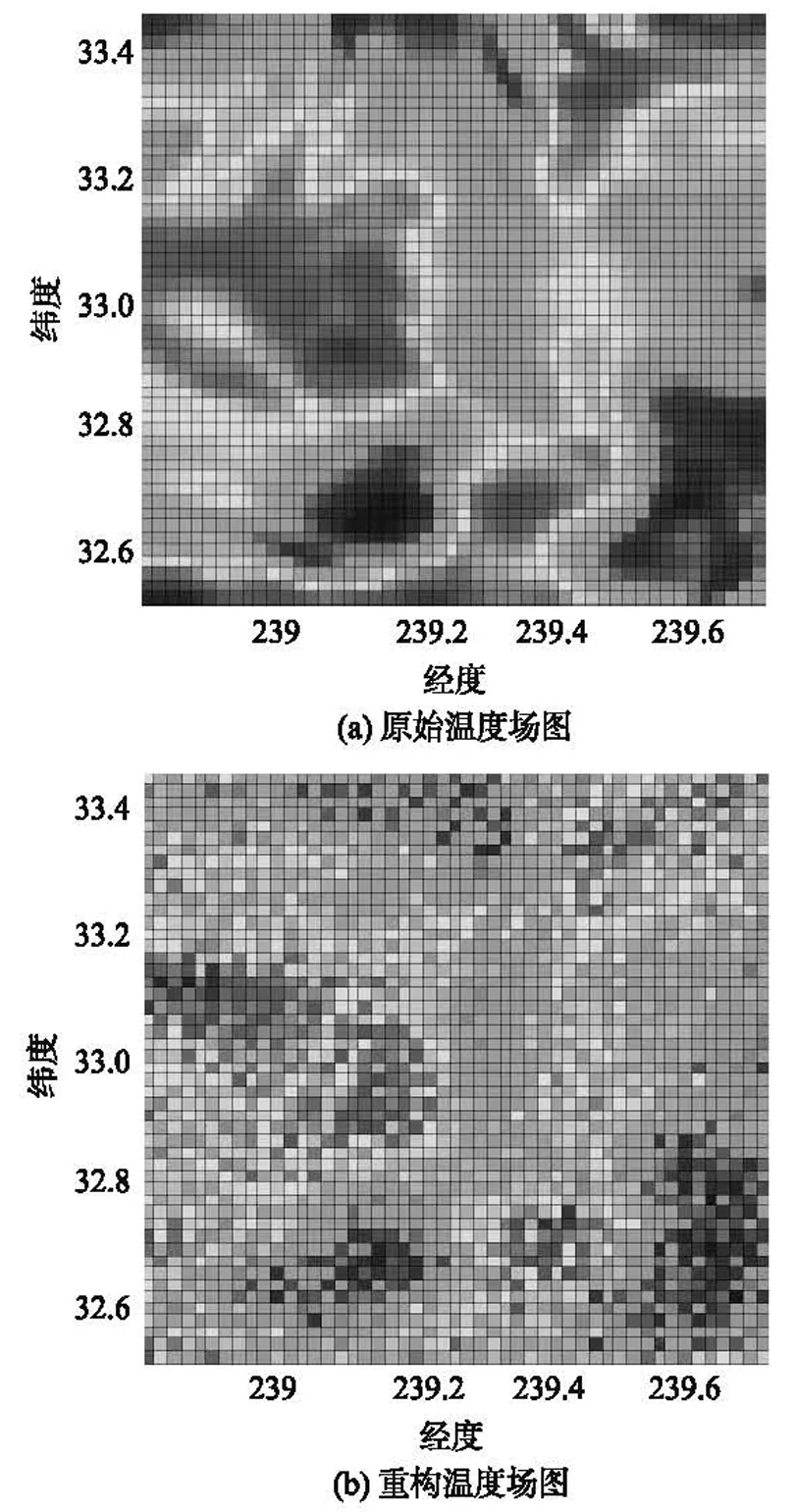
图2 传感器网络数据采集模型仿真结果
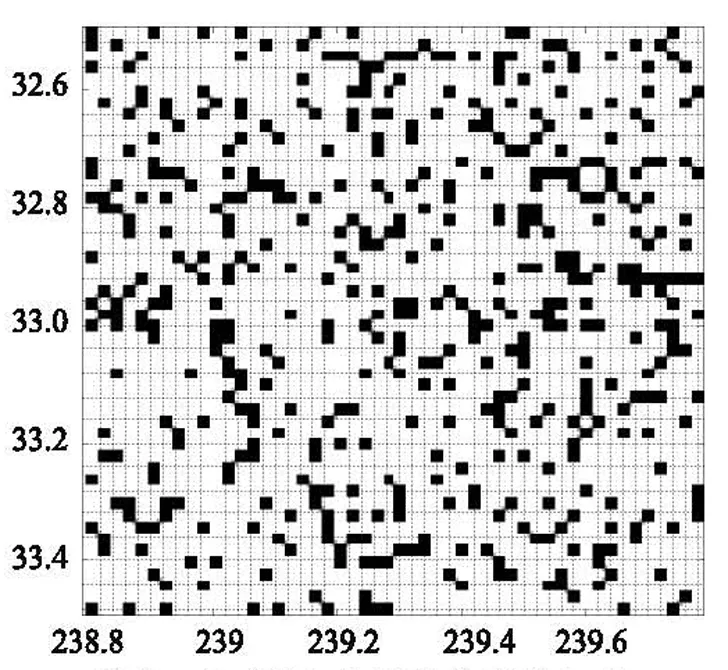
图3 成功随机观测到的区域分布
2 可调分辨率的重构方案
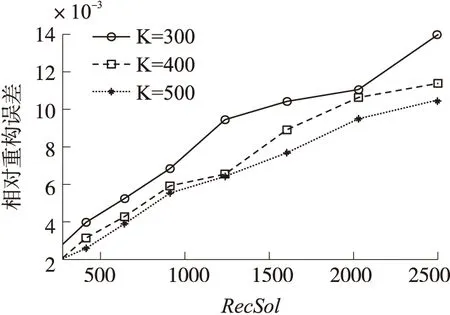
压缩感知理论表明,只要终端获取到的随机观测值的数目大于Ns=CSlogN,终端就能够以较高的概率唯一的恢复出原始信号。其中,N为原始信号的维度,S为原始信号的稀疏度,C为与N、S无关的常量[9]。所以,可以根据Ns和N的关系,动态的调整重构分辨率,以保证重构精度。然而,在实际的传感器网络应用场景中,要兼顾重构分辨率和重构精度这两个性能指标。所以,给出建议方案:首先,系统给定重构分辨率上限:SolUp,下限:SolLow,以及Sink节点实现对观测区域的压缩感知所需要的随机观测值的数目的门限值:Ns。其中,在给定重构精度以及重构分辨率要求的条件下,可以通过数值仿真获得Ns。图4给出了数值仿真求解过程,以2012年5月16号格林尼治时间,南加州海岸纬度[32.50,33.48],经度[238.80,239.78]地区测量得到的温度数值作为实验数据,在系统要求的相对重构误差的最大值为0.01,重构分辨率上限为2 500的条件下,数值仿真得出K=460,即Ns=460。

图4 数值仿真求解Ns
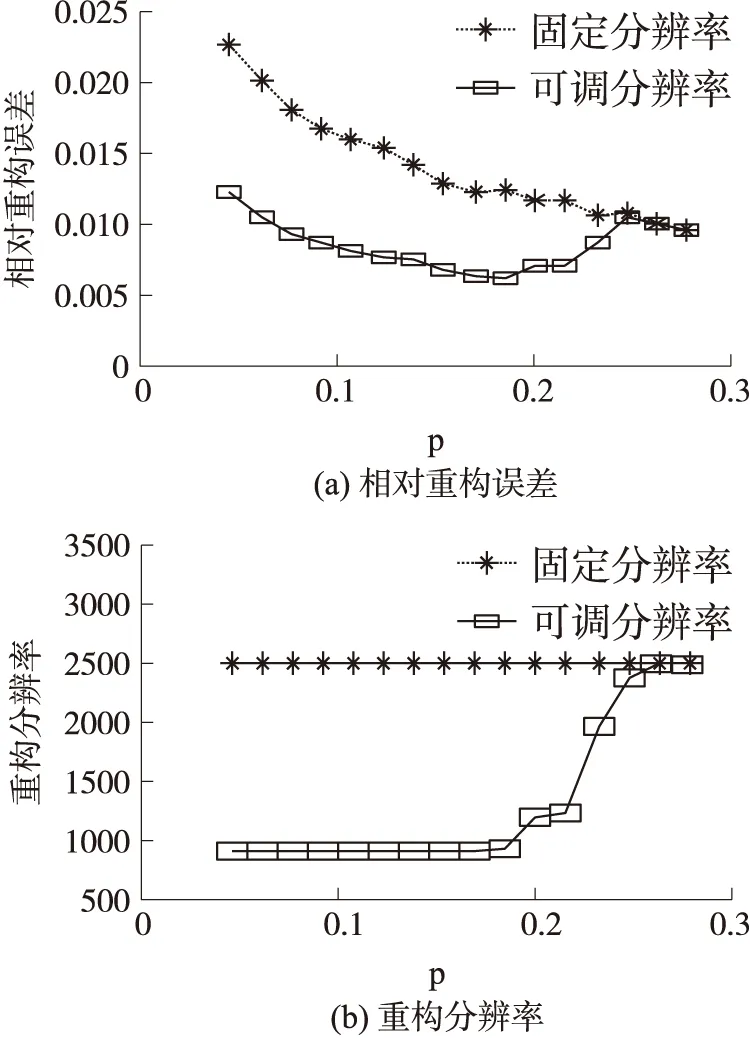
当K≥Ns时,Sink节点能够以较高的概率达到系统要求的重构精度,实现对传感器网络测量数据的压缩感知。这时,重构分辨率设定为SolUp。当K RecSol=2K/(CS) (3) 式中:RecSol为重构分辨率,K为Sink节点在一个数据帧的时间内成功接收的数据包的个数即获取到的随机观测向量的维度。如果RecSol 信息重构方案总结如下:在第n帧结束时,Sink节点获取到的随机观测向量为Y(n),其维度为K。Sink节点采用上文的分辨率调整策略计算出重构分辨率RecSol。然后,Sink节点根据重构分辨率RecSol对观测区域以网格的形式进行区域划分。如果有两个或者两个以上的被成功获取到测量数据的传感器节点处于同一个网格区域中,那么,这个区域的测量数据为该区域中被获取到的测量数据的平均值。按照这种方法,Sink节点对随机观测向量Y(n)进行处理得到Y′(n)。然后,Sink节点根据重构分辨率RecSol以及被成功观测区域的位置信息构造观测矩阵Φ(n)。最后,Sink节点采用l1最小化算法重构出分辨率为RecSol的原始物理信息。 为了详细的说明数据重构方案中对于随机观测向量Y(n)的处理方法和随机观测矩阵Φ(n)的构造方法,采用图5中的例子进行说明。在该例子中,假设待观测区域的大小为10×10,在每个1×1的网格区域的中心布置一个传感器节点,其中含有黑色圆圈的网格为被成功随机观测到的区域。假设经过分辨率调整策略算出的重构分辨率为6×6。在图5(b)中,第五行第一列的网格区域中有两个传感器节点,那么,该网格区域的观测值为这两个节点测量数据的平均值。随机观测向量Y(n):Y(n)∈RK×1经过处理后为Y′(n):Y′(n)∈RK′×1,其中,K′≤K。 图5 对于随机观测向量的处理方法说明 图6 K=460时,不同重构分辨率时的相对重构误差 随机观测矩阵Φ(n)=[φ1,…,φK′]T为单位随机抽取矩阵,包含着被成功观测到区域的位置信息,其中φi∈RRecSol×1,i∈{1,2,…,K′}。例如,对随机观测向量Y(n)处理后得到的向量Y′(n)中的第i个元素为观测区域中第j个网格区域中的观测值,那么向量φi为从单位矩阵I:I∈RRecSol×1中抽取的第j列向量。 首先,文章不考虑传感器网络中随机观测的物理过程,也不采用上文的分辨率调整策略调整重构分辨率,而是仅仅根据仿真中给定的重构分辨率进行数据重构。在给定K=460时得到仿真结果如图6所示。在Sink节点获取到的随机观测向量Y(n)的维度K不同的条件下进行仿真,得到仿真结果如图7。从图6的对比中可以看出,随着重构分辨率的下降,相对重构误差逐渐降低。结果表明,在采用压缩感知的方式进行传感器网络信息重构时,降低重构分辨率可以在一定程度上提高重构精度。从图7中可以看出,在Sink节点获取到的随机观测向量维度K一定的条件下,相对重构误差随着要求的重构分辨率的增大而增大。重构精度和重构分辨率是一对矛盾的重构性能指标。在重构分辨率一定的条件下,相对重构误差随着Sink节点获取的随机观测向量的维度K的增大而减小。所以,当系统给定重构精度要求,Sink节点获取到的随机观测向量维度K不满足K≥Ns时,Sink节点可以通过降低重构分辨率来提高重构精度。例如,如果系统要求的相对重构误差的最大值为0.01,当Sink节点获取到的随机观测向量维度K=400时,Sink节点可以通过调节重构分辨率RecSol,使其满足RecSol≤2 000,来保证重构精度。 图7 K取值不同时的重构性能 Sink节点实现对传感器网络观测区域的物理信息的压缩感知包括两个阶段:对传感器网络观测区域的随机观测和对观测区域的物理信息的重构。文章的重点是可调分辨率的信息重构方式,所以,为了简单起见,对于对观测区域的随机观测阶段,Sink节点采用上一节的系统模型获取随机观测向量。因此,可调分辨率的系统信息获取方案总结如下: 步骤1 在每一个数据帧的开始时刻,传感器节点i进行贝努力试验。假设参与数据传输的概率为p,保持休眠状态的概率为1-p; 步骤2 如果节点i参与数据传输,那么节点i就把测量数据连同位置信息编码成Lbits的数据包。然后,节点i选择一个随机发送延迟时间θi,其中θi在[0,T-Tp-τmax]上均匀分布; 步骤3 对于由于发生数据包的碰撞或者信道质量较差导致的无法被Sink节点正确解调,译码的数据包,Sink节点简单的丢弃掉。在一个数据帧结束时,Sink节点获取到的随机观测向量为Y(n),其维度为K; 步骤4 Sink节点采用上文的分辨率调整策略计算出重构分辨率RecSol。然后,Sink节点根据重构分辨率RecSol对观测区域进行区域划分。如果有两个或者两个以上的被成功获取到测量数据的传感器节点处于同一个网格区域中,那么这个区域的测量数据为该区域中被获取到的测量数据的平均值。Sink节点按照这种方法对随机观测向量Y(n)进行处理得到Y′(n)。然后,Sink节点根据重构分辨率RecSol以及被成功观测区域的位置信息构造观测矩阵Φ(n)。最后,Sink节点采用l1最小化算法重构出分辨率为RecSol的原始物理信息。 图8 两种方案的重构性能对比 在数据采集的过程中,考虑数据包之间的碰撞,认为信道为理想信道进行仿真。给定系统参数:一个数据帧的时间长度T=1 000,数据包的时间长度Tp=0.2,重构分辨率上限SolUp=2 500,重构分辨率下限SolLow=900,Ns=460。图8展示了两种重构方案的重构性能随传感器节点的感知概率p变化情况。从仿真结果中可以看出,当节点的感知概率较小时,由于参与数据传输的节点数较少,Sink节点在一帧结束时获取到的随机观测向量维度较低,采用固定分辨率的重构方案,相对重构误差较大,重构精度较低;而采用可调分辨率的重构方案能显著的提高重构精度;当节点的感知概率较大时,参与数据传输的节点数较多,Sink节点在一帧结束时获取到的随机观测向量维度较高,两种重构方案的重构性能趋于一致,都能以较高的精度重构出待观测区域的物理信息。当节点感知概率大约小于0.18时,根据分辨率调整策略计算出的分辨率为SolLow,保持不变,随着节点感知概率的提高,Sink节点在一帧结束时获取到的随机观测向量的维度增大,相对重构误差减小;当节点感知概率大约大于0.18且小于0.24时,根据分辨率调整策略计算出的分辨率有所提高,相对重构误差相应的增大,但仍能满足精度要求。当节点感知大约概率大于0.24时,根据分辨率调整策略计算出的分辨率为SolUp,保持不变,相对重构误差随着感知概率提高而减小。可以看出,文章中的分辨率调整策略综合考虑了重构分辨率和重构精度两个性能指标。 针对水下复杂多变的通信环境,提出了一种动态调节重构分辨率的重构方案。Sink节点根据采集到的数据的维度,在保证重构精度的情况下,动态调节重构分辨率。文章在数据采集过程中只考虑了数据包之间的碰撞,没有考虑信道质量对数据采集过程的影响。接下来的研究工作是在数据采集的过程中,考虑水下信道质量变化的条件下,综合评估对比可调分辨率重构方案和固定分辨率重构方案的重构性能。 [1] Akyildiz I F,Pompili D,Melodia T. Underwater Acoustic Sensor Networks:Research Challenges[J]. Ad hoc Networks,2005,3(3):257-279. [2]Donoho D L. Compressed Sensing[J]. IEEE Transactions on Information Theory,2006,52(4):1289-1306. [3]刘亚,刘功亮,康文静. 压缩感知和LEACH结合的水下传感器网络信息采集方案[J]. 传感技术学报,2013(3):388-395. [4]吕方旭,张金成,石洪君,等. WSN中的分布式压缩感知[J]. 传感技术学报,2013(10):1446-1452. [5]王泉,张纳温,张金成,等. 压缩感知在无线传感器网络数据采集中的应用[J]. 传感技术学报,2014(11):1562-1567. [6]Quer G,Masiero R,Munaretto D,et al. On the Interplay between Routing and Signal Representation for Compressive Sensing in Wireless Sensor Networks[C]//IEEE Information Theory and Applications Workshop,2009:206-215. [7]Fazel F,Fazel M,Stojanovic M. Random Access Compressed Sensing for Energy-Efficient Underwater Sensor Networks[J]. IEEE Journal on Selected Areas in Communications,2011,29(8):1660-1670. [8]Shim B,Song B. Multiuser Detection via Compressive Sensing[J]. IEEE Communications Letters,2012,16(7):972-974. [9]Candès E J,Romberg J,Tao T. Robust Uncertainty Principles:Exact Signal Reconstruction from Highly Incomplete Frequency Informa-tion[J]. IEEE Transactions on Information Theory,2006,52(2):489-509. [10]Chen S S,Donoho D L,Saunders M A. Atomic Decomposition by Basis Pursuit[J]. SIAM Journal on Scientific Computing,1998,20(1):33-61. Compressed Sensing Recovery Algorithm with Adjustable Resolution for Underwater Sensor Networks* ZHAOWenQiang,HUBin,KANGWenJing*,LIUGongLiang (School of Information and Electrical Engineering,Harbin Institute of Technology at Weihai,Weihai Shandong 264209,China) Considering the characteristics in the process of information collection in underwater sensor networks and the restricted requirements of compressed sensing theory,the compressed sensing recovery algorithm with adjustable resolution for underwater sensor networks is proposed in this paper. Firstly,the Sink node computes the reconstruct resolution according to the dimension of the random observed vector and the strategy for adjusting resolution. And then,the random observed vector will be processed,and the observed matrix will be constructed according to the reconstruct resolution and the location information of the node data. Finally,the information of observed area will be reconstructed by compressed sensing recovery algorithm. Simulation results show that the proposed method can improve the reconstruct accuracy in a small sensing probability. underwater sensor networks;compressed sensing;reconstruct accuracy;reconstruct resolution 赵文强(1991-),男,山东滕州人,硕士生,主要研究方向为无线传感器网络,hitzhaowenqiang@sina.com; 胡 滨(1991-),女,辽宁沈阳人,硕士生,主要研究方向为无线传感器网络,hubin.in2012@gmail.com; 康文静(1978-),女,辽宁锦州人,讲师,博士,硕士生导师,主要研究方向为水下传感器网络,目标跟踪和图像处理,kwjqq@hit.edu.cn; 刘功亮(1979-),男,山东淄博人,教授,博士,博士生导师,主要研究方向为空天与水下通信、无线传感器网络,liugl@hit.edu.cn。 项目来源:国家自然科学基金项目(61371100);山东省优秀中青年科学家科研奖励基金项目(BS2012DX001);哈尔滨工业大学科研创新基金项目(HIT.NSRIF.2013136) 2014-07-08 修改日期:2015-03-16 C:7230 10.3969/j.issn.1004-1699.2015.05.019 TP393 A 1004-1699(2015)05-0723-06
3 结论





