欧拉参数的选择对小范围应变率场求解的影响

杨凯钧，袁 鹏，秦昌威

(1.武汉大学测绘学院，湖北 武汉 430079; 2.武汉大学卫星导航定位技术研究中心，湖北 武汉 430079)



欧拉参数的选择对小范围应变率场求解的影响

杨凯钧1，袁 鹏2，秦昌威1

(1.武汉大学测绘学院，湖北 武汉 430079; 2.武汉大学卫星导航定位技术研究中心，湖北 武汉 430079)

对比论证了不同欧拉矢量在小范围块体上对应变率求解的影响，并以安徽区域为例，得出了在相对小块体上求解应变率场后，由块体本身求得的自适应欧拉矢量比利用NNR-NUVEL1A提供的欧亚板块欧拉矢量更能反映其区域块体内部应变的结论。自适应欧拉矢量大大减弱了其所在块体的相对速度系统差，有效去除了其跟随大板块背景场的运动趋势，在有条件求得其自适应欧拉板块参数时，比利用大板块的欧拉矢量效果更好。

欧拉矢量； 速度场； 应变

一、引 言

块体的应变率场求解是研究其地壳构造和形变的重要方法，对地质灾害的预测和防范具有很重要的意义。小范围(特别是省级范围)的应变率场研究具有很大的价值，目前大多数学者利用GPS手段研究大范围大板块的应力场[1]，对于小范围块体的研究，其核心内容是其无净旋转基准下对应欧拉矢量的选择。本文以安徽地区为例，利用长时间的GPS观测资料(CORS网络)得到各个站点的速度场，可由此得出观测区域背景下的欧拉矢量，同时也可以利用欧亚板块背景下的欧拉矢量(NNR-NUVEL1A提供)来求得各个站点去除板块运动速度后的速度残差。由去除板块整体运动后的站点速度可求得各个区域的应变信息，以分析纯净的各个区域地壳的相对运动、碰撞、挤压等地壳信息[2]。

二、块体欧拉矢量

根据定点转动位移定理可知，定点转动刚体的任何有限位移等效于绕通过该定点的某轴的一次转动，并可用欧拉(Euler)矢量来定量刻画。欧拉矢量是表现地壳块体运动的基本参数，其表现形式[3]为

点位线速度与欧拉矢量的关系为

Vi=ω×ri

将地心坐标转换为球面坐标为

式中，ψ和λ分别表示纬度和经度。再将其转换到站心坐标系,仅考虑其平面二维速度下，得

由此可以构造误差方程，每个CORS站点可以列2个误差方程，本文采用安徽50个CORS站点2年的数据求得的速度场，得到了安徽区域无浄旋转的欧拉矢量

此外根据国际上通用的NNR-NUVEL1A模型，可以查询到安徽块体所在的欧亚板块的欧拉矢量[4]为

三、相对背景场运动的速度场

得到区域速度场后，为了真实反映区域内部地壳活动状况，需要去掉其所在块体的整体运动趋势。若不能有效地去除块体背景场的速度趋势影响，则很难通过应变反映块体内部之间的活动情况，其表现出的是具有统一趋势的拉伸挤压情况。目前常用的去除背景速度场的方法有两种：一是通过区域所在板块利用多种空间观测手段建立的NNR-NUVEL1A模型得到的欧拉矢量作为板块背景场；二是利用本区域的GPS观测资料直接反演求得的欧拉矢量作为背景场(如图1、图2所示)。

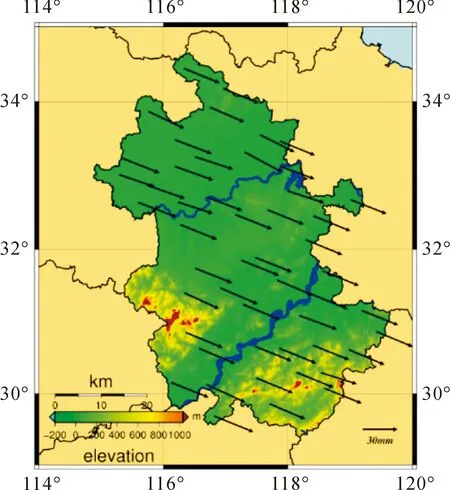
图1 安徽地区GPS 测站速度场

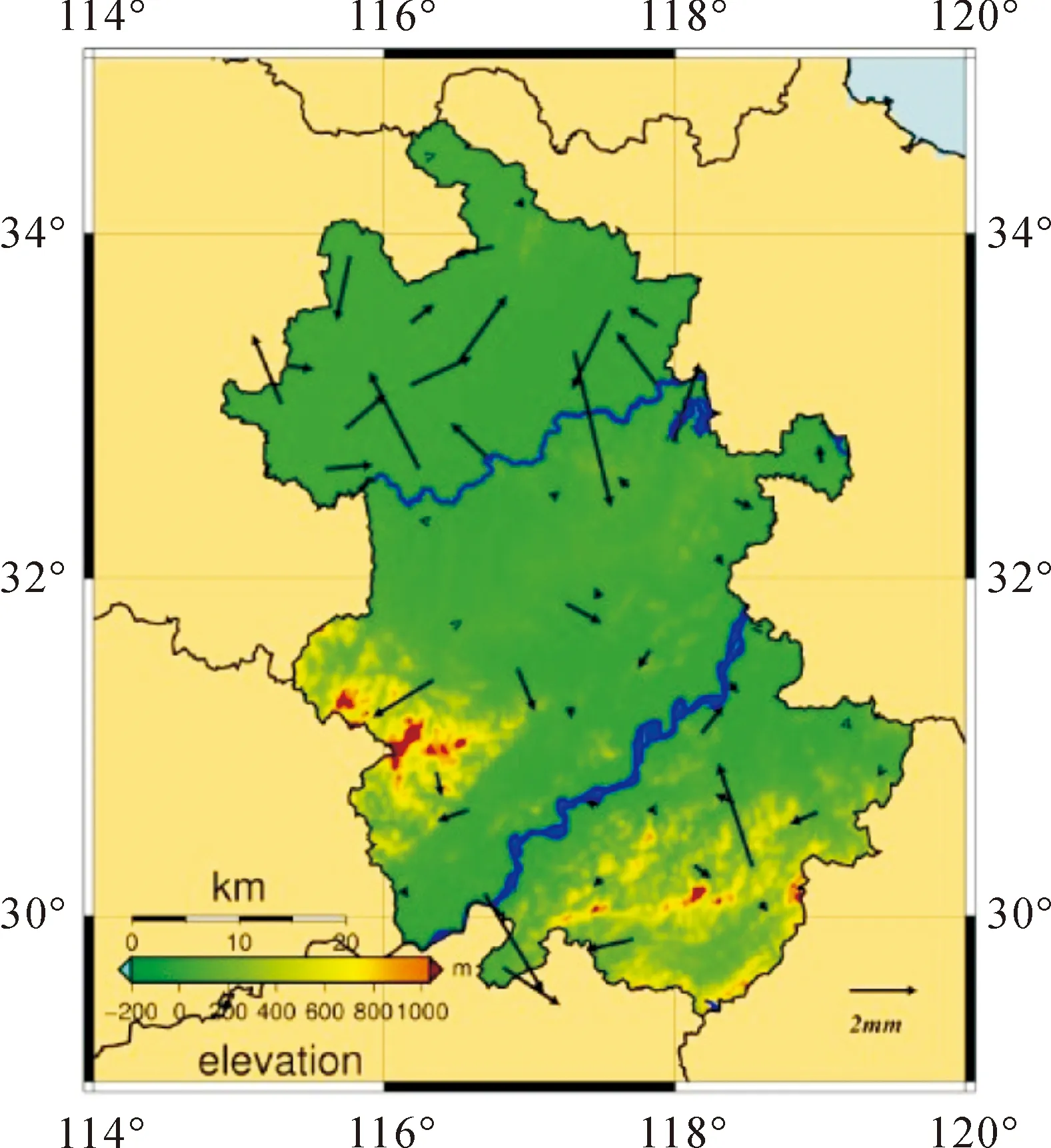
图2 除去区域块体整体运动趋势后的速度场

安徽块体在两个背景场欧拉矢量下的相对速度场可表示为

四、地壳应变率场的求解

利用去除背景场速度后的相对速度可以求解相应的应变率场[5-6]，即

其中，为了求解块体内各个部分的应变情况，需要对整体的GPS观测网进行划分，而将其构造成若干个Delaunay三角形是最好的划分方式(如图3所示)。每一个Delaunay三角形其重心可以求得一组应变信息。本文主要研究其主应变信息，编写了GeoStrain程序来构造三角网并计算其主应变[7](如图4、图5所示)。

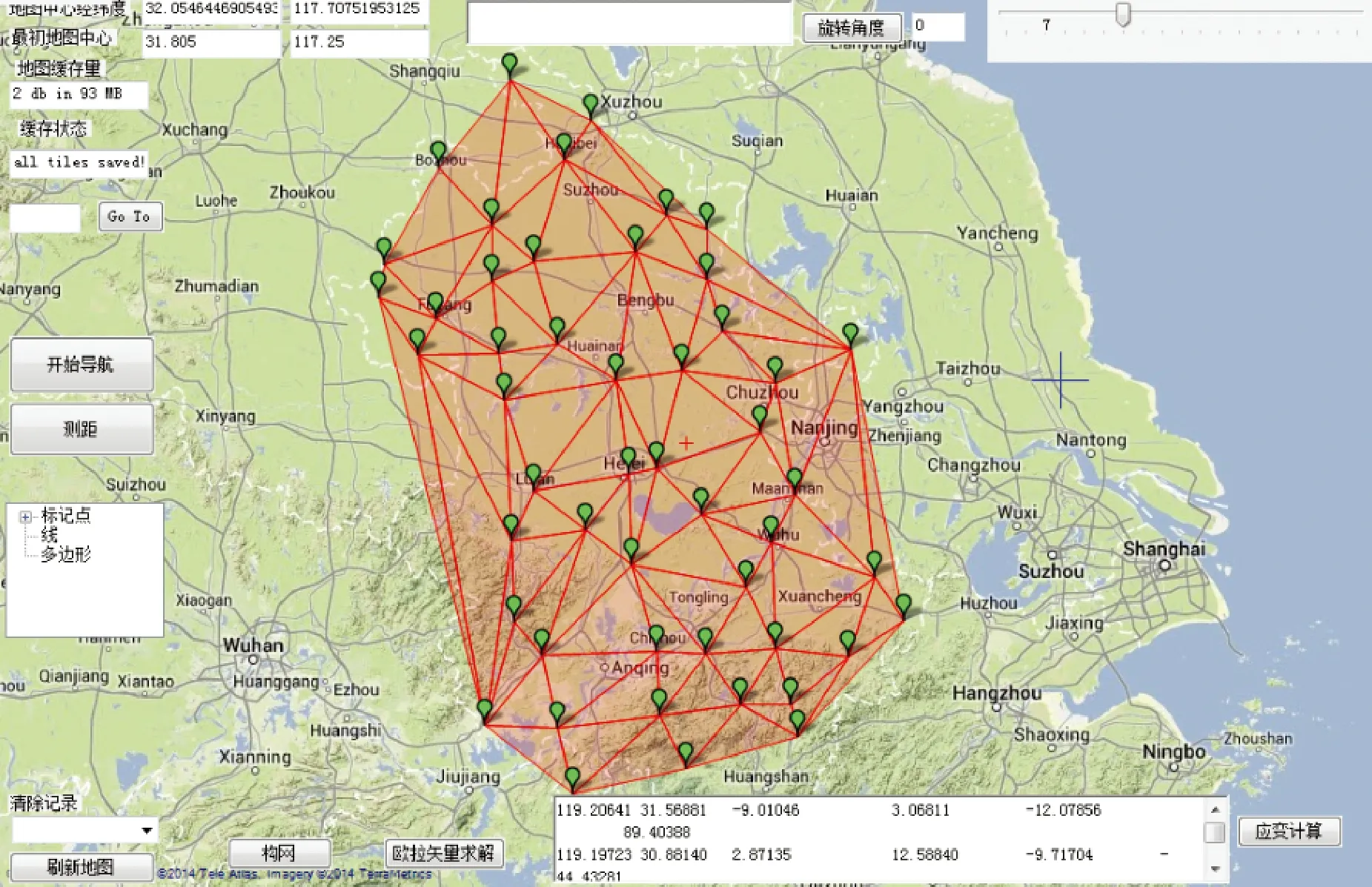
图3 GeoStrain程序截图

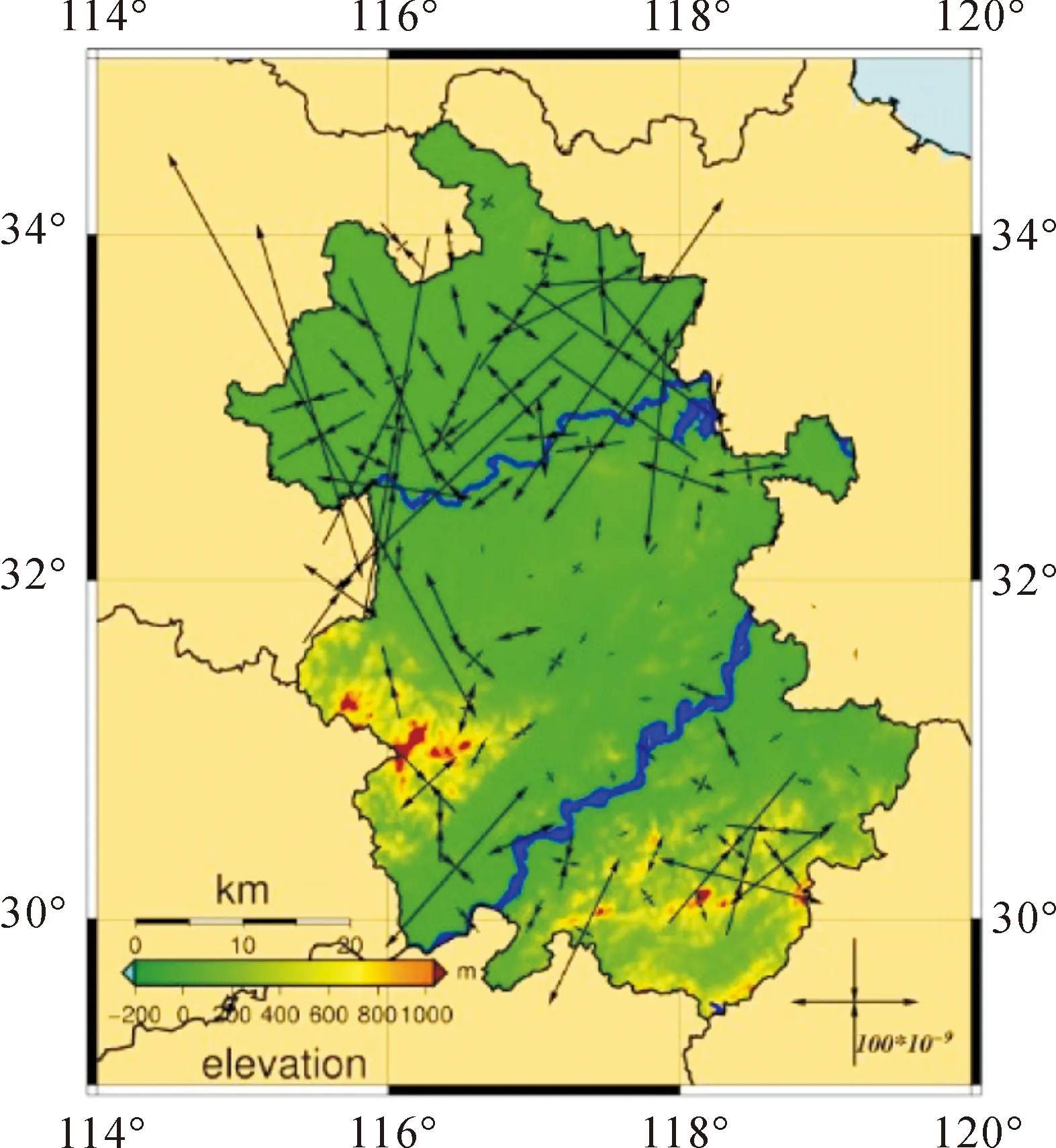
图4 除去区域块体整体运动趋势后的应变率场

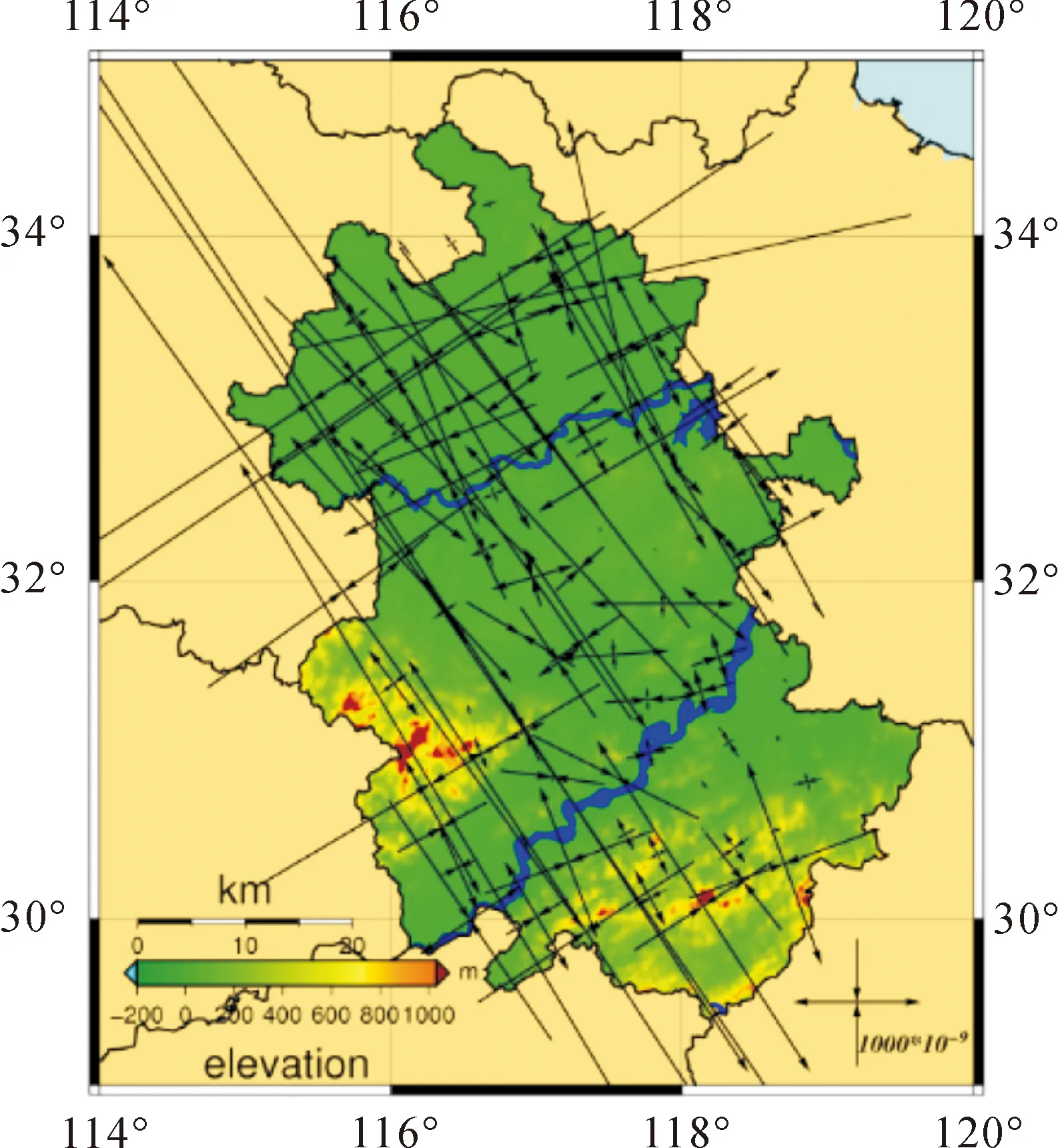
图5 除去欧亚块体整体运动趋势后的应变率场

五、结束语

通过由两种方法得到的安徽区域内部的应变率场情况可以看出，利用本区域GPS观测资料反演得到的欧拉矢量作为背景场得到的应变率场，整体上区域南部和北部应变剧烈，而中部地区基本稳定；淮河以北、长江以南及大别山区域是地壳活动剧烈带，其应变逐年积累，通过历史资料也可发现这些区域是地震多发地带。而利用欧亚大块体作为背景场得到的应变具有整体性的趋势：东南—西北方向拉伸，东北-西南方向压缩，趋势十分明显，而且整体应变强度比前者大一个数量级，足以证明后者并没有有效地消除背景场块体的影响，存在较大的系统性偏移。而利用本区域GPS观测资料反演得到的欧拉矢量作为背景场得到的应变率场很好地削弱了区域内随着块体整体偏移带来的影响，得到了具有较高参考价值的区域内部应变率场，突出反映了区域内部地壳的活动规律。因此在中小区域应变率场构造过程中，利用区域本身反演的欧拉矢量作背景场比利用所在大板块运动欧拉矢量作背景场更加精确可靠。

[1] 顾国华, 王丽凤.GPS观测得到的 1998—2003 年中国大陆地壳应变[J].地震, 2006, 26(3): 1-8.

[2] 沈正康, 王敏, 甘卫军, 等.中国大陆现今构造应变率场及其动力学成因研究[J].地学前缘, 2003, 10(S0)：93-100.

[3]LIY,YANGG,LIZ,etal.MovementandStrainConditionsofActiveBlocksintheChineseMainland[J].ScienceinChinaSeriesD:EarthSciences, 2003, 46(2): 82-117.

[4]ARGUSDF,GORDONRG,DEMETSC.GeologicallyCurrentMotionof56PlatesRelativetotheNo-net-rotationReferenceFrame[J].Geochemistry,Geophysics,Geosystems, 2011, 12(11)：75-87.

[5] 顾国华, 孙汉荣.利用GPS地形变资料在大地坐标系中计算应变[J].地壳形变与地震, 1998, 18(3): 26-31.

[6] 江在森, 张希.华北地区近期地壳水平运动与应力应变率场特征[J].地球物理学报, 2000, 43(5): 657-665.

[7] 孟国杰, 申旭辉, 伍吉仓, 等.GPS地壳形变监测网应变解算方法与程序设计[J].大地测量与地球动力学, 2006, 26(2): 70-74.

Influence of the Selection of Euler Parameters for Computing Strain Rate Field in Small Scale

YANG Kaijun，YUAN Peng，QIN Changwei

杨凯钧，袁鹏，秦昌威.欧拉参数的选择对小范围应变率场求解的影响[J].测绘通报，2015(7)：72-74.

10.13474/j.cnki.11-2246.2015.0215

2014-05-12

杨凯钧(1991—)，男，硕士生，主要从事GNSS精密数据处理研究。E-mail：apple-hacker@163.com

P223

：B

：0494-0911(2015)07-0072-03