一种改进的隧道盾构机姿态确定方法

龙四春，尹 炼，刘 德，张兆龙

(1.湖南科技大学煤炭资源清洁利用与矿山环境保护湖南省重点实验室，湖南 湘潭 411201；2.中建五局隧道公司，湖南 长沙 410004； 3.湖南科技大学能源学院，湖南 湘潭 411201)



一种改进的隧道盾构机姿态确定方法

龙四春1,3，尹 炼1，刘 德2，张兆龙3

(1.湖南科技大学煤炭资源清洁利用与矿山环境保护湖南省重点实验室，湖南 湘潭 411201；2.中建五局隧道公司，湖南 长沙 410004； 3.湖南科技大学能源学院，湖南 湘潭 411201)

在地铁隧道建设中，盾构施工日益普及，对盾构机姿态的精确定位是确保地铁贯通的必要条件。本文在分析与比较当前盾构机姿态确定主要方法与手段的基础上，结合三点法原理与建模理论，融合点面模型构建思想，提出了一种改进的三点法姿态确定方法，给出了该方法的数学模型，并用C#汇编语言实现了盾首和盾尾中心坐标的自动计算。结合深圳地铁某区间隧道，验证了该模型的工程应用与优势。

地铁隧道；盾构机姿态；三点法；点面模型

一、引 言

随着地铁的飞速发展，暗挖施工越来越普及，其中盾构法施工优势明显，具有掘进速度快，盾构的推进、出土、拼装衬砌等全过程可实现自动化，施工劳动强度低，不影响地面交通与地下管线等施工优点[1]。但在盾构施工中，需要实时确定盾构机的姿态及位置，以确保盾构机行进路线与设计路线间的误差在允许范围内[2]。

国内盾构机姿态确定主要是采用人工测量，并未形成导向系统。通过测量计算可以求出盾构的水平方位、盾构的翻滚角及坡度角，结合盾构内前标后标的几何关系，可得盾首、盾尾中心坐标，结合隧道设计轴线，就可以推算出盾构的尾平、尾高、切平、切高和推进里程。文献[2]研究了基于测量机器人对盾构机上两点进行三维坐标测量，结合盾构机上的精密测倾仪器进行盾构机姿态角测量，并在广州地铁4号线进行应用，提高了测量速度，但此方法需要较高的费用，数据处理时间也偏长。文献[3—14]对人工测量或机器测量方法进行了不同层次的改进与探索，但研究结果还未能形成一个独立的测量系统，还不能全自动为盾构机导航。

二、三点法及点面模型构建

1.三点法基本原理

三点法是利用盾构机内18个螺母点中的3个点，测量得到该3个点在施工坐标系中的坐标，然后利用几何关系或坐标转换求得盾首和盾尾坐标，再求出盾构机的姿态参数，三点法示意图如图1所示。

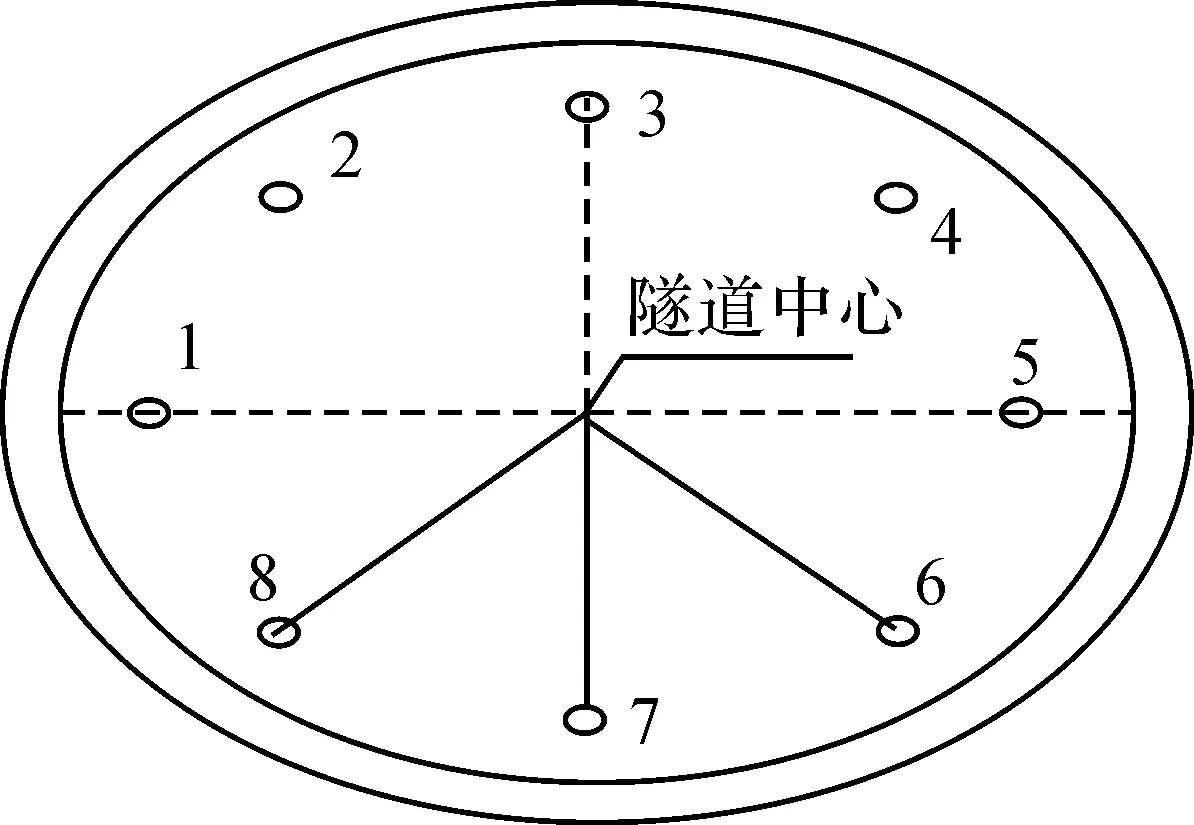
图1 三点法示意图

三点法坐标转换模型是将A点在两个不同坐标系中的坐标进行转换，求解出坐标的旋转矩阵、平移矩阵和缩放尺度，即将13个未知参数，包括旋转矩阵中9个方向余弦、3个平移和1个缩放尺度因子，利用归一化坐标转换公式消除坐标平移参数，根据旋转矩阵的正交特性，列出6个条件方程计算盾构机的姿态。坐标转换模型如图2所示。

几何原理是利用盾构系统中点到点之间的距离不变进行求解，可用一个三元二次方程组进行表达，即

(1)

式中，(x,y,z)为M螺母点在施工坐标系中的坐标；(X,Y,Z)为盾首或盾尾在施工坐标系中的坐标；(a,b,c)为测量点与盾首或盾尾坐标间的参数。

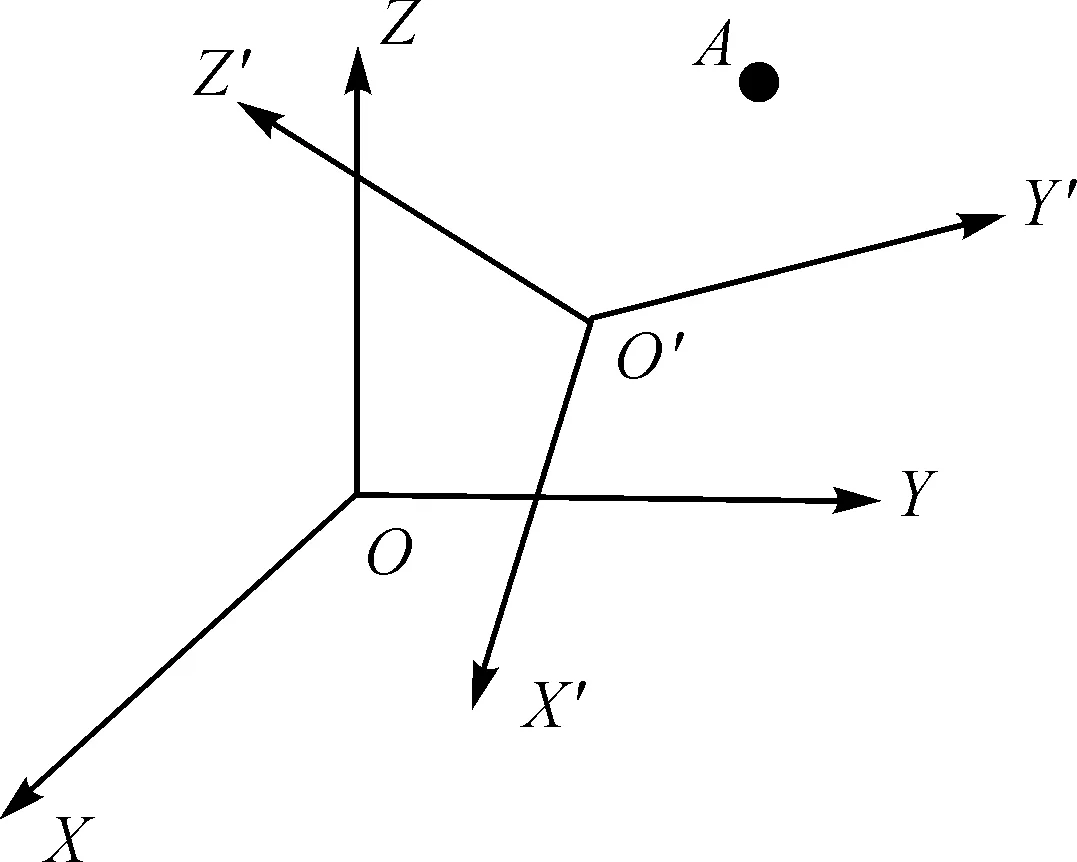
图2 坐标转换模型

可见，坐标转换需要求解坐标转换矩阵、平移矩阵和缩放比例，而几何原理需要求解三元二次方程，求解烦琐，不利于工程上高精度实时实现盾构机导向。

2.点面模型的构建

点面模型是在三点法原理的基础上，结合点到面的距离不变原理进行的。如图3所示，点O为盾首中心，点O′为盾尾中心，点1、2、3为盾构机内18螺母中的任意三点。由点1、2、3可以构成一个平面M123，则点O到平面M123的距离d不变，就可以求出盾首中心点O坐标。但在选择盾构机内的3个点时，应当尽量选择在盾构机内均匀分布的点，最好是分布在盾构机内的左、右、中部位。同时，要有多余测点作为观测量，以便平差，发现粗差，提高精度。

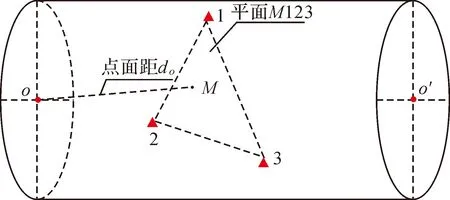
图3 点面模型

(1) 盾构机中心坐标计算

如图3所示，假设盾构机中，测得控制点1、2、3施工坐标为(xi,yi,zi)(i=1,2,3)，可推导出盾首中心坐标(xo,yo,zo)。由两点间的距离公式得

式中，d1o、d2o、d3o分别为点1、2、3到盾首中心O的距离。由于三点确定一个平面，因此，由点1、2、3可以组成平面M123。由已知三点求平面法向量得

(xn,yn,zn)=

(3)

式中，(xn,yn,zn)为平面M123的法方向矢量坐标。已知法向量求得平面方程为

xnx+yny+znz+D=0

(4)

将任一点坐标，如1点坐标，代入式(4)得

D=-(xnx1+yny1+znz1)

(5)

由点到平面距离公式得

(6)

式中，do为盾首中心点O到控制点1、2、3所组成平面M123的距离，可由盾构机就位后测量控制点1、2、3和盾首中心点O的盾构机坐标系坐标求出。

由式(2)、式(6)联立，可组成关于(xo,yo,zo)的三元一次线性方程组

(7)

由式(7)即可求得盾首和盾尾中心坐标。

(2) 盾构机姿态参数计算

由盾构机的盾首和盾尾中心坐标可以求出盾构机中心线与施工坐标系各个坐标轴的夹角，如与Z轴的夹角α可表示为

(8)

同理，由隧道设计线路可以求出该点的竖直角、俯仰角和横摆角。

3.点面模型的精度分析

在式(2)中，距离d1o、d2o、d3o是由盾构机参数计算得出的，一个盾构机的参数是在开工前就确定不变的，可以认为其为真值。则式(2)实际是由9个观测量与3个未知量组成的方程。将未知量(xo,yo,zo)看成观测量(xi,yi,zi)(i=1,2,3)的函数，则式(2)可表示为

(9)

由微分可得

dX=Fdx

(10)

式中

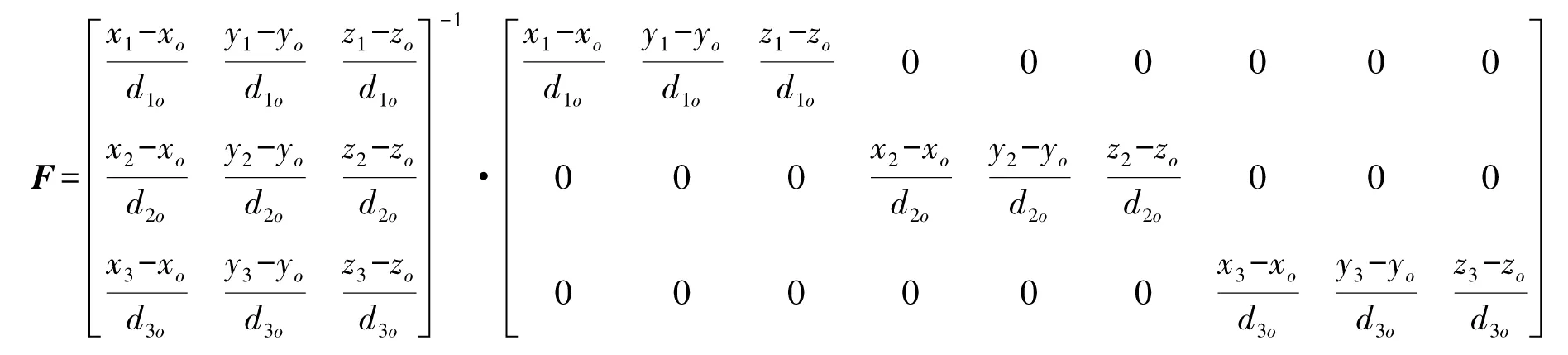
则根据协方差传播率有

DXX=FDxxFT

(11)

三、点面模型在深圳地铁9号线中的应用

1.工程与数据概况

深圳市轨道交通9号线路全长25.38 km，全部为地下线路，4次下穿、3次上穿既有铁路或地铁，穿越段均为盾构法施工。在该工程某盾构施工标段中，盾构机局部坐标系盾首中心坐标为(0,0,0)，盾尾中心坐标(-4.34,0,0)。盾构机内18个螺母控制点的盾构机局部坐标已知。在该工程的某些里程桩上，观测得到的施工坐标数据见表1。

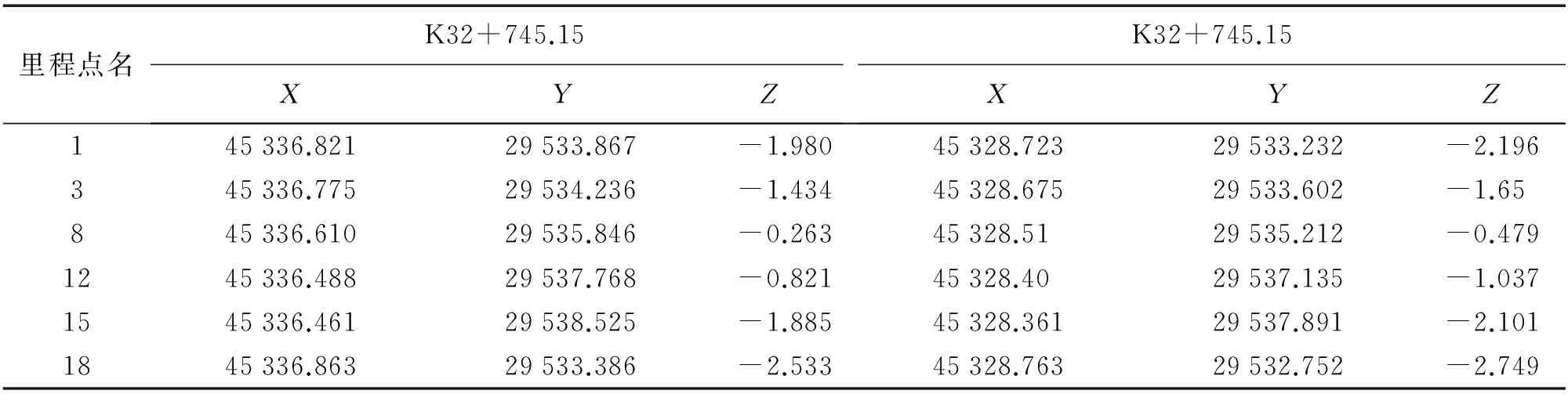
表1 控制点观测坐标 m

将表1中里程K23+750.15上3、8、15三点观测数据输入到自编程序中得到盾构机坐标，计算的盾构机姿态结果见表2。

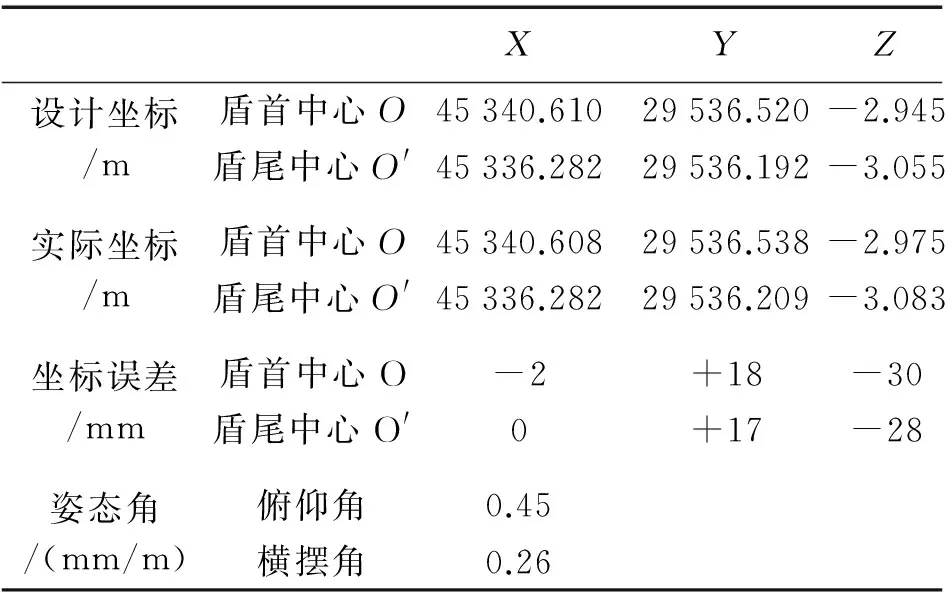
表2 盾构机姿态计算结果

注：“+”表示偏上或偏右；“-”表示偏上或偏左。

在施工设计标准中，只要盾构机的坐标偏差不大于10 mm，俯仰角不大于10 mm/m，横摆角不大于10 mm/m，就可认为盾构机导向系统是正确的。

2.精度分析

(1) 点位误差分析

点面模型测量采用不同的参考点会得到不同的盾构机中心坐标，解算结果见表3。

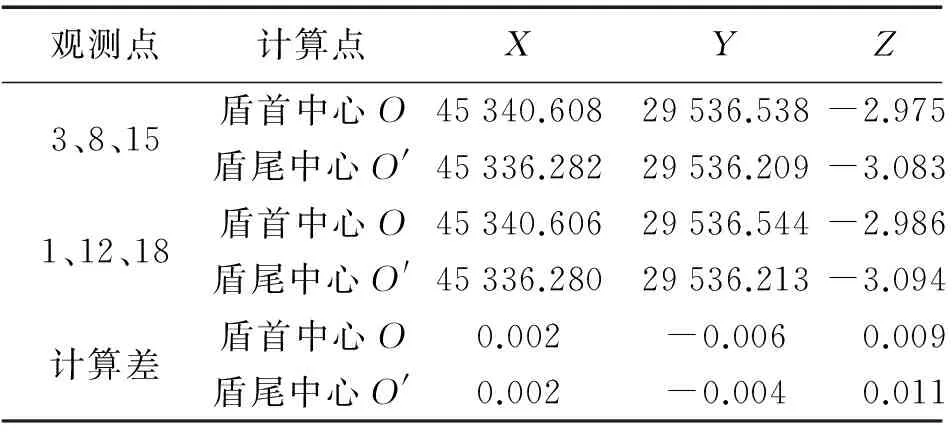
表3 不同控制点计算结果比较 m

产生误差的主要原因是控制点的观测值误差和点面模型误差。如选用仪器观测精度为3 mm(即表示X、Y和Z坐标的观测中误差为3 mm)，如表1中，在里程K23+745.15处观测的点3、8、15，利用随机函数，计算得到1000组数据，采用统计分析可得图4、图5和图6。

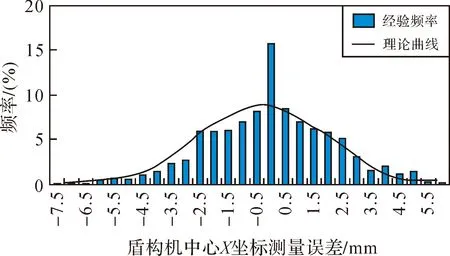
图4 盾构机中心X坐标测量误差统计

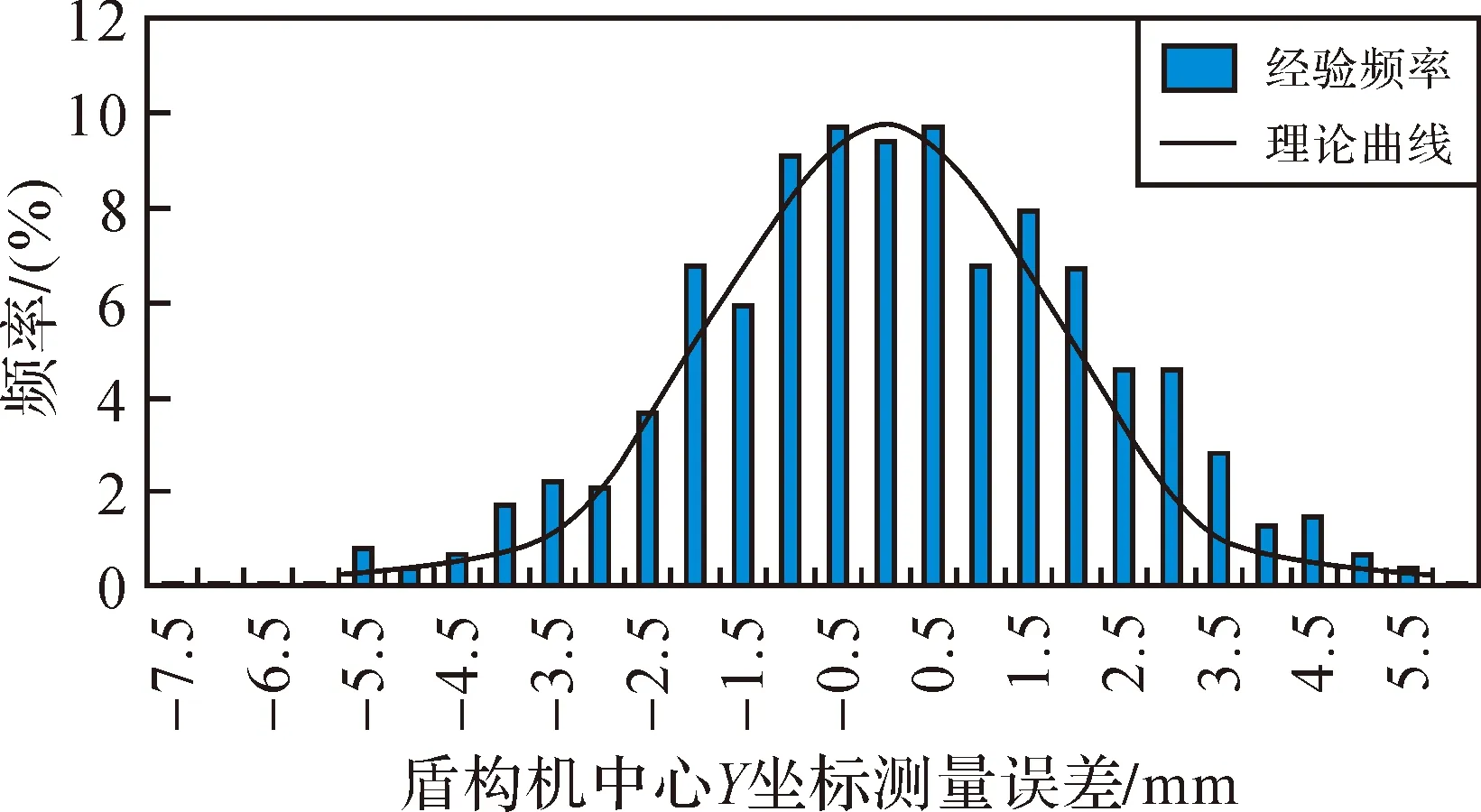
图5 盾构机中心Y坐标测量误差统计

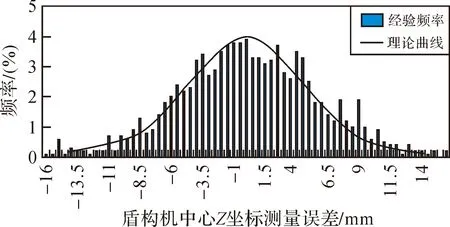
图6 盾构机中心Z坐标测量误差统计

从统计图中可以看出，点面模型计算得出的盾构机中心坐标，X、Y坐标相对Z坐标更为稳定。

(2) 姿态角误差分析

中心坐标误差可造成姿态角计算误差，对姿态角进行模拟计算，可得姿态角计算误差，统计结果如图7和图8所示。

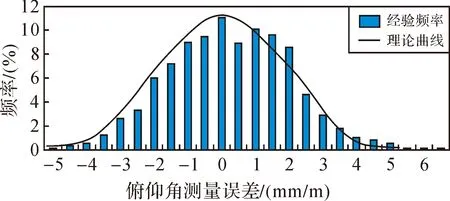
图7 盾构机俯仰角测量误差统计

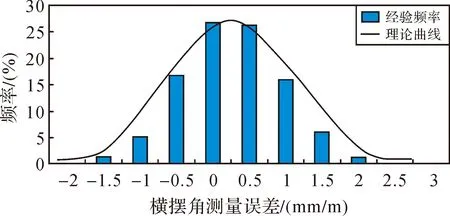
图8 盾构机横摆角误差统计

从统计图可以看出，两种角度测量误差也符合正态分布，但横摆角比俯仰角更稳定，误差更小。

四、结束语

利用点面模型可以精确地计算得出盾构机中心坐标，提高人工测量与计算处理的速度，减少劳动力，简化计算过程。并在建立模型的基础上，将该方法汇编成程序自动实现。但点面模型只能测量计算出盾首、盾尾中心坐标，以及盾构机俯仰角、横摆角，无法计算出扭转角。该方法同样存在因选取不同的控制点与观测点，导致计算精度有微变，应使选取的测量控制点最好呈锐角三角形分布，且应当尽可能使三角形边距最大。在盾构姿态确定过程中，应选取多点观测，得到多余观测量，以便测量计算结果更加稳健。同时，采用更高精度的测量仪器，将会提高测量精度。

[1] 方坤.盾构法地铁施工测量若干问题研究[D].南京:南京工业大学,2011.

[2] 唐争气,赵俊三,彭国新.盾构机实时姿态测量和计算方法的研究[J].土木工程学报,2007,40(11):92-97.

[3] 潘明华.盾构机自动导向系统的研究与实现[D].武汉:华中科技大学,2005.

[4] 张厚美,古力.盾构机姿态参数的测量及计算方法研究[J].现代隧道技术,2004,41(2): 14-20.

[5] 欧阳平,吴北平,刘建强,等.几种盾构机姿态测量方法的精度比较[J].工程地球物理学报,2006,3(4):304-309.

[6] 王维.地铁盾构法施工人工导向测量研究[D].南京:南京工业大学,2008.

[7] 潘国荣,李怀锋,王穗辉.盾构姿态自动导向及多源数据融合处理方法[J].同济大学学报：自然科学版,2013,41(4):619-623.

[8] 潘国荣,周莹,张德海.坐标转换模型在盾构姿态计算中的应用[J].大地测量与地球动力学,2006,26(3):84-87.

[9] 薄志义,王坡,张楠.盾构机轴线方位角解算原理研究[J].北京测绘,2006(3):18-21.

[10] 任福松,金建俊.地铁施工中的盾构机姿态控制研究[J].交通标准化,2009(9):134-137.

[11] 王超领,张永超.地铁盾构机掘进实时姿态定向测量的研究[J].隧道建设,2007(6):33-35.

[12] 陈慧.基于无衍射光的盾构位姿测量系统的理论与技术研究[D].武汉：华中科技大学,2011.

[13] 凌颜芳.盾构机掘进过程中轨迹规划问题的研究[D].大连：大连理工大学,2009.

[14] 吕向红.盾构机姿态精度控制技术[J].隧道与地下工程,2012(4):108-111.

An Improved Positioning Method of the Attitude of Tunnel Shield Machine

LONG Sichun，YIN Lian，LIU De，ZHANG Zhaolong

龙四春，尹炼，刘德，等.一种改进的隧道盾构机姿态确定方法[J].测绘通报，2015(7)：46-49.

10.13474/j.cnki.11-2246.2015.0208

2014-08-13

国家自然科学基金(41404106；41004002)；大地测量与地球动力学国家重点实验室基金(SKLGED2014-5-3-E)；桂科能基金(1207115-21)；煤炭资源与环保湖南省重点实验室基金(E21221)

龙四春(1975—)，男，博士后，副教授，主要研究方向为大地测量与形变监测。E-mail: sclong@hnust.edu.cn

P258

：B

：0494-0911(2015)07-0046-04