命题处处陷阱解题步步为营——导数问题求解中的“对而不全”揭秘

☉江苏省海安县曲塘中学夏秀梅

命题处处陷阱解题步步为营
——导数问题求解中的“对而不全”揭秘

☉江苏省海安县曲塘中学夏秀梅

每次考试后总有一部分同学感觉良好，但成绩并不理想，究其原因是问题解答中没有注意到一些细节，造成“对而不全”现象，致使整体成绩不理想·高考试题中解答题要求严密的推理、详细的解答，其分值设置是按步骤得分·本文以笔者所教授的班级中部分同学在解答导数问题中的“对而不全”问题为例进行说明·

一、忽视隐含条件——对而不全

（1）当a=0时，求函数f（x）的图像在点（1，f（1））处的切线方程；

（2）如果对于任意x1，x2∈R，且x1＜x2，都有f（x1）＜f（x2），求a的取值范围·

解析：（1）略·

（2）先考查函数g（x）=-x2+2x-3，x∈R的图像，配方得g（x）=-（x-1）2-2，所以函数g（x）在（-∞，1）上单调递增，在（1，+∞）上单调递减，因为对于任意x1，x2∈R，且x1＜x2，都有f（x1）＜f（x2）成立，所以a≤1·

以下考查函数h（x）=xlnx，x∈（0，+∞）的图像，则h′（x）=lnx+1，令h′（x）=lnx+1=0，解得

例1已知函·随着x变化时，h（x）和h′（x）的变化情况如下表：

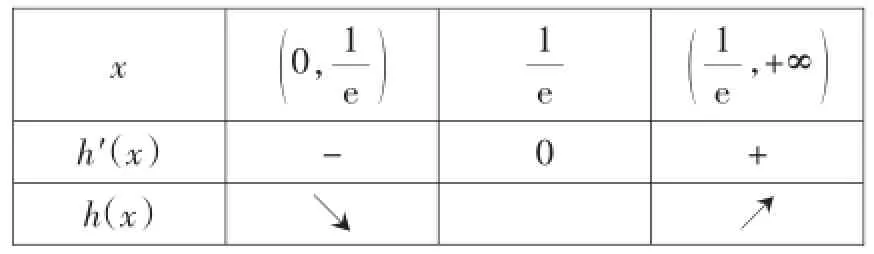
x 0，1（）1（）1 e e e，+∞h′（x）-0 + h（x）↘↗

若对于任意x1，x2∈R，且x1＜x2，都有f（x1）＜f（x2），则g（a）≤h（a），即-a2+2a-3≤alna，解题无法继续……

揭秘：本题解法受常规解题思维的影响，欲使函数在整个定义域内单调，则在分段点的函数值大小关系为-a2+2a-3≤alna，但此不等式不易求解·挖掘解题过程

二、忽视构造新函数——裹足不前

导数问题一直是高考的压轴题，解题中常需要构造函数，如何构造既是难点，也是热点，近年高考题中出现了很多需要构造函数的题，还有一些是二元变量的最值问题，这更是让学生感觉无从下手·值大于零？若存在，请求a的取值范围；若不存在，请说明理由·

例2

（1）当a≤0时，f′（x）＞0在（0，+∞）上恒成立，故无极值·

（2）当a＞0时，-ax2+x+1=0，Δ=1+4a＞0且两根之积为极值点是无理的，若直接代入函数f（x）中，不可能求出参数a的取值范围，那么如何求参数的范围呢？

揭秘：可以通过消参，构造函数求出极值点x2的具体范围，从而求出a的取值范围·

因为x1＜0，x2＞0，即求使f（x2）＞0的a的取值范围，过程如下：构造函数g（x）=lnx+，g（x）在（0，+∞）上单调递增且g（1）=0，故g（x）=lnx+＞0，得x＞1，即x=2

三、忽视对问题的探究——思维中断

四、忽视解题方法的优化——避简求繁

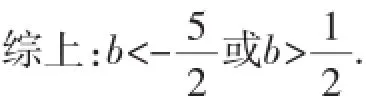
揭秘：一般地在涉及二次函数在区间上有零点或最值的问题上，通常研究的方法都是利用其对称轴与定义域区间的位置关系生成分类讨论的标准，然后再逐步依据题目的要求将问题予以解决，此种做法易想能做，但解题过程繁杂，能否找到有效回避分类讨论的处理呢？

解法2：考虑到h（0）=1＞0，问题的对立面为方程（fx） =x在区间（-1，1）上无解，即函数h（x）=区间（-1，1）上无零点，

一个数学问题通常都具有两面性，当一方较为烦琐的时候，往往其对立面一般就会稍显简单，解法2正是有效利用这一点，使解题过程得到了简化·

总之，中等难度的题目是高考试题的主要构成，是大部分考生得分的主要来源·对于中档题，考生普遍存在的现象是“得分容易，得满分难”，要解决“会而不对，对而不全”的问题，解题中要注意规范审题、规范书写过程、深入挖掘隐含条件、深入反思·F