分层教学模式在高中数学课堂中的应用探讨
☉浙江省玉环县玉城中学蒋永斌
分层教学模式在高中数学课堂中的应用探讨
☉浙江省玉环县玉城中学蒋永斌
随着近年来教育改革的逐步推进,高中教学也逐步面向素质教育和寻求创新模式加强教育水平,促进教育发展·高中教育作为以高考为主要目标的教育形式,如何在以应考为导向的教育方式中,积极正确地开拓新型教学模式、提高教学水平、促进教育发展成为高中教育者的重要任务·在学生成绩和知识掌握水平参差不齐的情况下,为了使得每个学生个体得到最好的发展和提高,分层教学模式应运而生·
一、分层教学模式在高中数学课堂中应用的现状
1·分层教学模式在高中数学课堂中应用的背景
在以高考为目标导向的高中教育阶段,高中数学一直被视为十分重要的学科之一,同时也成为令许多学生头疼,被视为难以提高成绩的学科之一·20世纪80年代,分层教学开始传入我国,随着近年来教育逐渐迈向素质教育和“以人文本”的教育体制的逐步兴起,分层教学模式的研究逐渐深入,相关实践及试验也方兴未艾·90年代末,许多中等职业学校对分层教学展开了不同形式的研究和探索·
2·分层教学模式在高中数学课堂中应用的缺陷
分层教学的理论基础是科学合理的,并且在实践中也已经取得了很大的成效,但是在实践调查中却发现,分层教学在实践中存在一系列的问题·由于分层教学的实践操作在我国教育界起步较晚,缺乏相应经验,教师、学生、家长习惯于传统的统一教学模式,实际操作中并没有处理好实际操作的问题等原因,分层教学在高中数学教学应用中并没有完全成功·
3·分层教学模式在高中数学课堂教学中的问题
据大量国内的高中数学分层教学实例显示,分层教学主要问题包括:首先,国内的分层教学模式是停留在对国外借鉴的基础上,然而国外的教育情况与我国不同,要实行高中数学分层教学切不可照搬照抄,教育工作者应该针对我国的以高考为导向的目标评价机制,思考分层教学的出路所在·作为一项涉及面广,系统且复杂的工作,学校针对分层教学的制度不健全,教师的探索与制度不一致或者超出制度范围等现象没有灵活处理,这在很大程度上束缚教师的隐性分层教学·
二、分层教学模式在高中数学课堂中的应用建议
1·在显性分层的基础上进行隐性分层
分层教学要重视显性分层,更不能忽视隐性分层·在通过充分地了解学生成绩与学习能力之后,科学、合理地进行显性分层·如,针对成绩不同进行年级分班,尽量保证同一班级的学生学习成绩接近·分层教学应该是流动性的,根据一段时间学习之后,再次按照分层教学的依据划分层次,使学生能及时根据学习能力调整层次,获得需要的学习机会和资源·这种流动性也是对学生的一种鼓励机制,实时清晰自我定位,激发学习热情·
2·对学生及家长做好思想工作
学校要及时对学生展开思想工作,激发学生的学习积极性和兴趣,促进学生努力学习·部分家长认为普通班或差班师资力量落后,学校对学生不够重视,从而对学生未被分到优班而内心不理解,这些问题学校也要及时说明分层教学的目的和具体措施,争取家长的理解和支持·
3·教学内容分层
教学内容分层包括教学课堂形式和教学评价目标分层,根据分层学生的学习情况分别制定不同的教学目标和教学形式,科学地制定合理的教学计划,针对基础较差的学生要求掌握基础的简单的数学能力,针对基础中等的学生制定学习计划要求掌握大纲对学生提出的知识应用能力,针对成绩优秀的学生所要求的目标应该是在熟练掌握和灵活运用的基础上开阔眼界、激发潜力·以人教版高中数学教学为例,利用均值不等式解题分为:牢记并简单运用、熟练运用、完全掌握并灵活创新三大不同层次,具体教学内容和目标应该分别制定·用定义求圆锥曲线的焦半径时目标应该分为:能够正确理解公式、简单运用公式求得焦半径;能够掌握圆锥曲线的图像、相关运算及应用,能理解并应用公式;熟练掌握并加深理解,灵活运用等三大方面·2

成绩基础较差的学生要求掌握第一级难度,因此在该题的解法上,为加强理解,可以先用代数法基本判断该函数的单调性·成绩基础不错,但举一反三能力一般的学生要求掌握第二级难度,即能运用课堂数学方法顺利解出此题·第三级难度较大,需要学生有坚实的数学基础和触类旁通的数学敏锐性,可以在此题顺利解出后进行数学延伸和继续扩展·
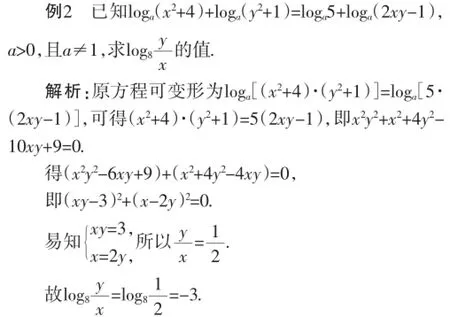
该题对学生掌握函数的能力要求较高,综合了对数函数和幂函数的应用,针对成绩较差的学生,理解函数的混合较为困难,因此应该在讲解此题之前要求其复习一遍对数函数和幂函数的性质·成绩一般的学生,应该要求其顺利地解出此题,灵活运用函数的性质·对成绩优秀的学生,不能仅完成题目,要以此为基础研究各函数混合的难题应用,提高函数掌握水平·
三、分层教学模式在高中数学课堂应用的实例探讨
在高中数学必修1中,函数及其表示是重难点,对于初中基础较差或者对函数本质没有清晰理解熟练掌握的学生来说,学习过程较为艰难·函数包含内容众多,无论是基础题、中等题还是难题,都时常涉及这一章·在函数的三要素:定义域、值域和对应法则中,求值域或最值是考试常见的题型之一·常见方法有观察法、判别式法、不等式法、换元法、反函数法、数形结合法及函数的单调性法等·对于基础较差的学生,面对众多方法无所适从,教师应该从巩固基础的目标出发,先让学生熟悉最为简单的观察法,培养学生学习信心和学习热情,在此基础上进行能力提高——教授判别式法,将“求f(x)的值域”这一问题可转化为“已知关于x的方程y=ax2+bx+c有实数解,求y的取值范围”,进而利用判别式法,b2-4ac<0无根,b2-4ac=0有两个相等根即一个根,b2-4ac>0有两个不相等根·对于学习基础一般中等的学生,应该在巩固基础的同时使得解题能力向较高难度过渡,在熟练掌握判别式法的基础上练习不等式法、换元法、反函数法等·而成绩优异的学生则可以根据能力省去基础简单题型的练习,向高难度题型发展,开拓眼界,发掘潜能·
第一类习题,要求了解椭圆的形状、特性、焦半径等,能熟悉椭圆各个公式的具体含义,能熟记简单基础的公式进行代入计算·
例3椭圆的左、右焦点分别是F1、F2,P是椭圆上一点,则△PF1F2的周长为()·
A.10B.16C.18D.20
第二类习题,理解椭圆公式的产生,体会椭圆数形结合的思维方式,能熟记相关椭圆公式,进行公式计算,对一般椭圆题型能进行计算,掌握一般解决椭圆问题的解题方式·
A(.0,3)B(.3,4)
C(.0,3)∪(4,+∞)D(.0,2)
第三类习题,在熟练掌握公式和椭圆数形结合之后,能灵活运用椭圆的性质,结合其他数学知识灵活运用,进行知识迁移·
四、小结
分层教学通过区分对待使得学生能在自身群体中准确找到自身定位,从而充分发掘自身潜能与学习积极性,根据自己的能力来选择定向培养目标·分层教学在我国应用时间较短,取得了一定成效,但是仍存在较多的问题有待解决·高中数学的分层教学模式在我国逐渐得到重视,然而实施过程中受到诸多限制,如,理论与实际应用环境不符、教师对于分层教学的认识不够深入、学生家长的不理解与不支持、学校相关制度的漏洞等,针对原因提出的建议主要有以下几种,在显性分层的基础上进行隐性分层、对学生及家长做好思想工作、教学课堂形式和教学评价目标分层·
1·阮如辉·分层合作教学模式在高中数学课堂的应用[J]·师道·教研,2014(7)·
2·张峰·浅谈高中数学课堂班级分层教学[J]·网络导报·在线教育,2012(16)·
3·周永善·高中数学课堂班级分层教学模式研究[J]·当代教育论坛,2011(6)·F

