由一道高三试题的命制历程感悟解析几何复习
☉浙江省富阳中学钱丽谈
由一道高三试题的命制历程感悟解析几何复习
☉浙江省富阳中学钱丽谈
笔者有幸参加了浙江省新高考研究联盟2015年第一次联考数学(文科)的命题工作,对其中第22题的命制与打磨有很多的思考与感悟·
一、试题
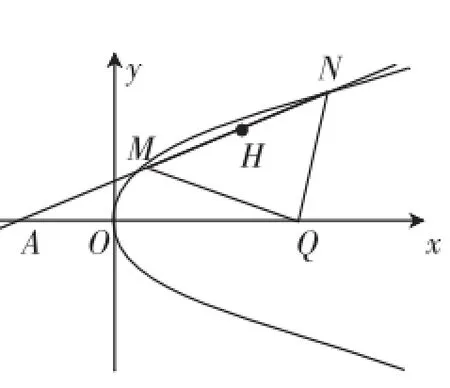
已知抛物线C:y2=4x,直线l:y=kx+2(k>0)与抛物线C交于M、N两点,与x轴交于点A,H为MN的中点,O为坐标原点·
(Ⅱ)设点Q在x轴上,记以QM、QN为邻边的菱形面积为S1,三角形AHQ的面积为S2,求的取值范围·
二、命题立意
接到任务之后,笔者重新做了近三年浙江省文科高考试题,纵观近三年高考,作为压轴题的解析几何试题基本稳定在考查抛物线的几何性质,直线与抛物线的位置关系,同时考查解析几何的基本思想方法和运算求解能力·因此,确定本次的命题立意:以抛物线为载体,考查抛物线的标准方程、几何性质,直线与直线、直线与抛物线的位置关系等基础知识,考查运算能力与推理论证能力,体现解析几何以代数方法解决几何问题的特质·之后,围绕这个主题,得到本题的初稿:已知抛物线C:y2=4x,直线l:y=kx+2(k>0)与抛物线C交于M、N两点,与x轴交于点A,H为MN的中点,O为坐标原点·
(Ⅱ)在x轴上是否存在点Q(m,0),使得以QM、QN为邻边的四边形是个菱形?若存在,求出m的范围;若不存在,请说明理由·
三、命题打磨
1·题目数据的打磨
解析几何问题的基本解法是以代数方法研究几何问题,因此,无论是在编题还是在解题的过程中都要重视“数”与“形”的精准对接,在命制试题的过程中,应对自己给出的文字和图形进行反复推敲·
本题第一问设问“是否平行”,暗示学生要验证直线与抛物线是否有两个交点,获取参数k的取值范围,可以很好地考查学生思维的严谨性·但是当我们从图形表征的角度,将直线2x+y-2=0和抛物线在同一直角坐标系中画出来之后,发现直线OH的斜率是正的,而直线2x+y-2=0的斜率为负的,肯定不可能平行,有的同学一看图就可以看出答案来了,达不到“以代数方法研究几何问题”的目的,所以将本题中的直线方程改为“2x-y-20”·
2·题目问题的打磨
本题的两个问题都是存在性问题,带有重复的味道,而且考查的知识也比较单一,直线与圆锥曲线的位置关系中涉及的弦长、距离等重点知识未涉及,不能突出平时学习的重点,因此,我们想将第二问设计为求一个函数的最值,这样更贴近高考,同时也加大本题对思维能力和运算能力的要求·
2015年的高考与以往有所不同:文科高考不考导数,因此,最后的最值问题不能用导数来解决,只能设计为用基本不等式或者已学过的函数的最值求解,另一方面,本题中的菱形面积可以巧妙地将解析几何中的“中点、垂直、弦长”等常考知识点进行串联,可以很好地考查学生数与形的转化能力·最终,我们从数学简单美的角度选取了以QM、QN为邻边的菱形面积S1和三角形AHQ的面积S2为研究对象,定稿为求的取值范围·

显然,解法2思路简单,但是计算太烦琐,学生必须要有很好的数据化归能力和很强的计算能力,才能彻底计算到底,而解法1从整体上考虑问题,不必去算Q的坐标以及三角形和菱形的面积,大大简化了计算量·这两种不同的解法体现了学生思维的不同层次,既可以使基础弱的学生能上手解题,也可以使基础好的学生思维得到发挥,具有很好的区分度·
与初稿相比,定稿在语言上显得更精练,更明晰;在问题的设计上显得更丰富,更饱满;在问题的解答上显得更有层次感,我们认为是一道好题·
四、对解析几何复习的几点感悟
1·钻研高考题,准确定位复习目标
俗话说“知己知彼,百战百胜”,作为教师,不仅要认真研读课程标准与考试说明,更重要的是要积极钻研高考题·教师的研题与学生的做题在本质上是完全不同的,教师在研题过程中往往会重点思考出题意图,题目的本质,学生的困难所在,教学的重点等·
通过大量的解题活动,教师能更清晰地知道学生的解题盲区,能更好地提炼出适合学生的解题方法和指导策略,理解题目的内涵,领会考查意图,同时也能很好地感受近几年解析几何高考在考察内容、考察方式上的稳定与变化,从而在复习的过程中才能找准复习重点,设立准确的教学目标·
2·运用多元表征教学策略探寻解析几何解题思路
表征是指信息或知识在心理活动中的表现和记载方式,具有多种形式——文字表征、图形表征、符号表征,许多研究表明:问题解决者的表征在他们解决问题中起关键作用·
解决解析几何问题的基本方法是以代数方法研究几何问题,在解题过程中,首先需要将文字信息与图形条件进行对应与互补,通过用代数语言描述几何要素及其关系,将已知的几何条件表示成代数式子,然后进行适当的代数运算得出代数结果,最后通过分析代数结果的几何含义解决几何问题·在这个复杂的过程中,要经历文字表征、图形表征和符号表征之间的多种转换·因此,我们必须重视对解析几何问题的表征教学,帮助学生利用多种表征形式表征同一关系情境,以及促进对这些表征之间等价关系的理解,从而促进学生构建属于自己的问题表征,形成正确的问题解决策略·
不同的表征方式可以提供不同的解题思路,如本题对题目条件“以QM、QN为邻边的菱形”的图形表征如下所示·
文字表征是:①菱形是邻边相等的平行四边形;②菱形的对角线互相垂直平分·
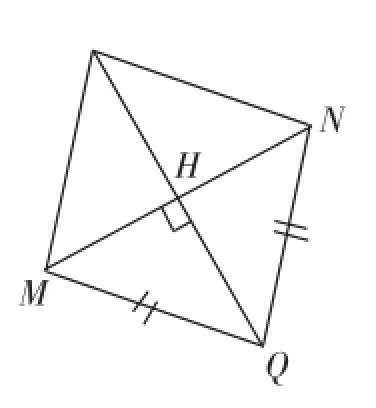

通过对图形表征到文字表征、文字表征到符号表征的转换,最终可以得到3种不同的代数表征,而这三种不同的代数表征就是三个解题突破口,可以得到三种不同的解法·
正如认知心理学家西蒙所说的:“如果一个问题得到了正确的表征,可以说它已解决了一半·”因此,在解析几何的复习中,教师要将问题的不同表征作为教学的重点内容,尽可能地启发学生从不同的角度表征题目的已知条件和目标结论,使学生在丰富的表征情境中获得开阔的解题思路,达到思如涌泉的境界·
3·运用简化计算的策略突破解析几何的解题瓶颈
解析几何以代数方法解决几何问题的特点使得解析几何问题的解决往往涉及烦琐、冗长的运算,这不仅影响解题的速度和准确度,还会使学生陷入解题困境,丧失解决问题的信心·我们在平常的教学中,经常会遇到这样的现象:学生有解题思路,但是总算不到底,学生对解析几何的印象也只有一个字:繁·所以如何简化计算应成为解析几何复习中要着重解决的任务·
就本题而言,可以运用以下三种简化计算的策略·
①整体代换简化计算·见本题上述参考答案的解法1·
②探寻几何意义简化计算·本题若选用上述向量表征进行解题,会涉及以下烦琐的计算:MN的斜率k,问题就可以迎刃而解了·
③消元简化计算·设而不求是解决解析几何问题的通法,在解决几何问题的过程中,往往会涉及很多变量,面对这么多的变量,学生往往感觉无从下手,从而放弃计算·如对于本题,很多学生选用菱形邻边相等的性质束手无策了,实际上,在解题时使得变量越少越好是一x2=2m-4这样一个简单的式子·
总之,解析几何的复习既要有“条条大路通罗马”的探索精神,更要有“走最短的路到罗马”的优化思想

