齿轮测量中心测头球心位置的标定

李伟

（沈阳飞机工业（集团）有限公司，沈阳110034）

0 引言

随着现代制造技术的不断发展，对于加工精度和加工效率的要求越来越高，数字化闭环制造是提高加工精度和加工效率的重要手段，而实现数字化闭环制造的关键环节就是对被加工工件进行精确的测量［1］。对于齿轮制造业而言，为了实现数字化闭环制造，需要利用齿轮测量中心或三坐标测量机测量出实际加工齿面相对于理论齿面的偏差，然后再将偏差反馈给设计分析软件，计算出实现偏差修正的参数，进而实现数字化闭环制造。为了提高齿轮测量的精度，本文针对采用电感式一维测头的齿轮测量中心，运用最小二乘法，根据采集到的标准球球面上点的空间坐标，拟合出标准球球心的坐标，并将测球球心在机器坐标系中的位置转换到测量坐标系，实现了对测头球心位置的标定。

1 标准球球心坐标的计算

在标定测球球心坐标的过程中，需要利用标准球间接地确立测量坐标原点的位置，从而计算出测球球心相对于测量坐标系的位置。计算标准球球心坐标，实际上是将采集到的一系列的标准球球面上的点运用最小二乘法进行拟合，最终计算出标准球球心在机器坐标系中的坐标。采集点的位置的选择以及采集点数量会影响拟合精度进而影响测量结果。采集点的位置和采集点数量的设置，如图1和图2所示。

在确定测球球心到被测工件定位基准面的距离时，只需保证Z方向的精度，因此采用图1所示的摸球策略。为确定标准球球心在机器坐标系中的R、T、Z三个方向的坐标，此时需要同时保证三个方向的精度，因此采取图2所示的摸球策略。本文所用的测头是一维测头，测头只能在一个方向上受力，采用图1所示的摸球策略时应调整测头使其在Z方向受力，采用图2所示的摸球策略时应调整测头使其在T方向受力。

图1 摸球策略一

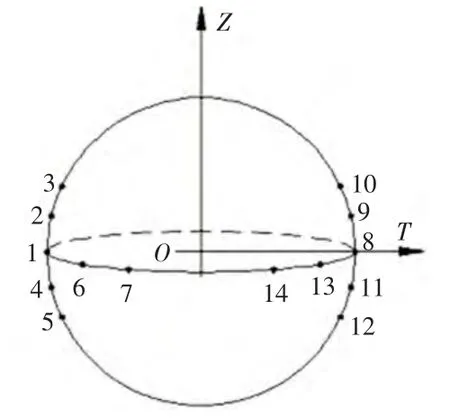
图2 摸球策略二

设所采用的标准球球心在机器坐标系中的坐标为（A，B，C），标准球半径为r，则标准球球面的方程可以写成如下形式：

令 a=-2A，b=-2B，c=-2C，d=A2+B2+C2-r2，则标准球球面圆的方程可写成

根据实际采集到的标准球球面上的n（n=7，14）个采样点Pi（xi，yi，zi）的坐标值，利用最小二乘法拟合出被测标准球的球心坐标和半径。由式（2）可知，标准球球面被测点Pi（xi，yi，zi）的残差为

由式（4）可知，L（a，b，c，d）大于或等于零。因此，该函数必然存在大于或等于零的极小值，它的极大值为无穷大。将函数 L（a，b，c，d）分别对参数 a、b、c、d 求偏导数，令偏导数等于零就可求出该函数的极值点。将式（4）分别对a、b、c，d 求偏导数得

式（6）中的 E、F、G、H、I、J、K、M、N 可由被测点的坐标Pi（xi，yi，zi）及被测点的数量n计算得到。解三元一次方程组式（6）可得到 a、b、c的值，将得到的 a、b、c的值带入到式（5）的第4个式子中，可求出参数d的值，则标准球球心坐标及半径为：

2 测球球心位置的标定

根据齿轮测量中心的测量原理，测量齿轮齿形误差时，测球球心的运动轨迹是由输入的齿面理论数据来决定的［2-4］。因此，要想测球球心按照给定的理论数据进行测量，必须将测量坐标系、机器坐标系和工件坐标系统一。

图3 测头中心位置标定

2.1 旋转工作台中心的坐标计算

本文采用的测头为瑞士TESA电感式一维测头，测量过程中，测头只能在一个方向受力，因此，在测量不同的工件或不同的项目时，需要适当改变测头受力方向或调整测头安装位置，而每调整一次测头，都需要对其中心坐标进行标定。由于被测工件是安装在旋转工作台上的，此时，旋转工作台的回转轴线基准不能用来标定测球球心的位置。本文采用的办法是：用固定于旋转工作台的标准球来标定测球球心在测量坐标系中的坐标。测头中心位置的标定，实际上是确立测量坐标系原点的过程。如图3所示，A，B两点分别为标准球球心绕Z轴旋转θ角度前后的位置，其矢量分别为Ra、Rb；O点为机器坐标系原点；O′点为转台中心线在RT平面中的位置，其矢量为RO′。

设O′点以及A、B两点在机器坐标系中的坐标分别为（x0，y0，z0），（x1，y1，z0），（x2，y2，z0）。由图中几何关系可知，|O′A|=|O′B|，则有

上述方程中的 x1、y1、x2、y2、z0为 A、B 两点的坐标，即标准球球心在机器坐标系中的坐标，已由最小二乘法求得，θ的值由圆光栅记录下来。x0、y0为旋转工作台的中心在R、Z平面中的坐标值，为未知数。解上述方程组即可求出x0、y0的值，从而求出旋转工作台在机器坐标系中的坐标。

2.2 测量坐标系的建立

以锥齿轮齿形误差测量为例来说明测量坐标系的建立方法。锥齿轮的轮齿坐标系的原点设定在齿轮的轴交错点上［5-6］。因此，需要将机器坐标系的原点转换到齿轮的轴交错点上，并将轮齿坐标系作为最后的测量坐标系。设标准球球心与被测齿轮安装基准面之间在Z轴方向的距离为d1，安装距为d。齿轮的轴交错点在齿轮轴线上，而齿轮轴线与旋转工作台的轴线是重合的。因此，齿轮轴交错点在机器坐标系中的坐标应为（x0，y0，z0+d1+d）。设测球球心在机器坐标系中的坐标为（x′、y′、z′），那么测球球心以齿轮轴交错点为原点时的空间坐标为

式（7）就是测球球心的坐标从机器坐标系向测量坐标系的转换公式。

3 结论

1）运用空间矢量运算和最小二乘法建立了测头标定的数学模型。2）利用最小二乘法拟合了标准球球心，计算并得到了标准球球心在机器坐标系中的位置。3）运用空间矢量运算，建立了将测球球心的坐标从机器坐标系向测量坐标系进行转换的方法。

［1］ 黄新冠，邓效忠，李天兴.弧齿锥齿轮齿面偏差测量［J］.机械传动，2007，31（6）：67-69.

［2］ 徐彦伟，张连洪.基于齿面点坐标测量值的弧齿锥齿轮齿面建模［J］.制造业自动化，2014（9）：34-37.

［3］ 王建华，劳奇成，刘波，等.CNC齿轮测量中心的原理、特点及关键技术［J］.工具技术，1996，30（3）：41-43.

［4］ 张树坤，孙秀文，黄杰，等.3906型齿轮测量中心测量与控制系统［J］.计量技术，2003（11）：33-34.

［5］ 吴大任，骆家舜.齿轮啮合理论［M］.北京：科学出版社，1985.

［6］ 曾韬.螺旋锥齿轮设计与加工［M］.哈尔滨：哈尔滨工业大学出版社，1989.