高速立式加工中心滚珠丝杠螺母副动态特性分析

桂 翔，汪永明

(安徽工业大学机械工程学院，安徽马鞍山 243032)

现代数控机床正向着高速化、高精度化、复合化和环保化方向飞速发展［1］，这对高速立式加工中心的进给系统提出了越来越高的要求。国内外学者对滚珠丝杠副的动态特性做了许多研究，如宁怀明等［2］运用有限元分析软件对丝杠进行了模态分析，研究了无阻尼自由振动时的丝杠，得到了系统的固有频率和振型;谢黎明等［3］考虑轴承结合部对丝杠动态特性的影响，对丝杠进行了模态分析和谐响应分析，验证了丝杠在有效转速范围内不会发生共振，得出了谐响应振幅最大时的频率;侯秉铎等［4］以超精密滚珠丝杠进给系统试验台为研究对象，提出了一种新的进给系统有限元模型，对其工作台进行了谐响应分析;安琦瑜等［5］针对某数控龙门镗铣床滚珠丝杠进给系统，探讨了有限元模型中结合面的建模方法，并进行了动态特性分析。以上文献的研究均未能全面考虑滚珠丝杠螺母副的支撑方式及运动状态等因素。本文以某型号高速立式加工中心为研究对象，通过对高速立式加工中心滚珠丝杠螺母副的不同支撑方式和螺母运动状态分别进行有限元模态分析，并对两端固定支撑方式下的多种螺母运动状态进行轴向正弦载荷激励下的谐响应分析，为今后的设计提供理论依据。

1 滚珠丝杠螺母副的有限元建模

有限元计算的准确性取决于正确有效的有限元模型的建立［6］。根据高速立式加工中心的设计要求，按照常规滚珠丝杠副的选型方法，针对X方向进给系统的滚珠丝杠螺母副进行选型设计，采用台湾TBI的SFS型高速静音滚珠丝杠，型号为SFS02020－2.8，丝杠公称直径为 20mm，导程为20mm，螺纹升角为 18°42'，丝杠长度为 1 238mm，滚珠圈数为2.8×1，滚珠直径为3.175mm，滚道直径为5mm，最大转速为3 000r/min。为了验证选型的正确性，需对其进行动态特性分析。

首先，采用SolidWorks2011软件对设计的滚珠丝杠螺母副进行三维实体建模，并对三维实体模型进行以下简化和特别处理:

a.去除键、圆角和安装其他装置的螺纹。

b.省去丝杠外螺纹滚道、螺母内螺纹滚道和滚珠，用弹簧单元 Combine14代替［7］，在这里取两列，一列四组弹簧布置，如图1所示。

将建好的三维模型保存为x_t格式导入Hypermesh11.0软件，定义其单元类型为Solid185，选定的材料属性为是轴承钢，型号为GCr15，弹性模量 E=2.19 ×1011N/m2，泊松比 ν=0.3，密度 ρ=7.83 ×103kg/m3。弹簧单元类型为Combine14，根据文献［8］计算得出其弹性刚度为6.1×108N/m。采用六面体网格划分，导出格式为.cdb，用 ANSYS14.5软件读取并进行相应的分析处理，得到有限元模型如图2所示。

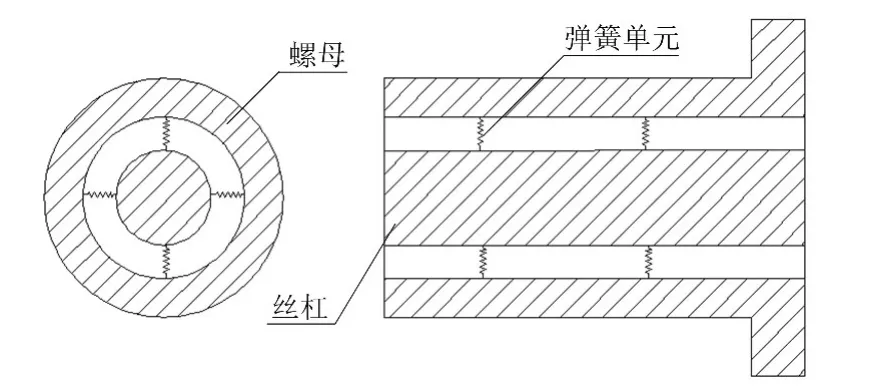
图1 丝杠与螺母间等效弹簧布置

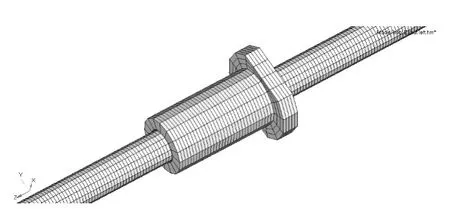
图2 滚珠丝杠螺母副的局部有限元模型

2 滚珠丝杠螺母副的模态分析

为了研究高速立式加工中心的动态特性，针对其不同支撑方式和螺母处于不同丝杠位置的固有振动特性进行模态分析。滚珠丝杠螺母副的支撑方式主要有:两端固定、一端固定一端支撑和一端固定一端自由3种。前两种刚度较大，考虑到高速立式加工中心的设计要求，仅分析前两种支撑方式下的模态。

2.1 两端固定支撑方式下的模态分析

2.1.1 螺母运动到最左侧时的模态分析

将Hypermesh划分好的网格以.cdb格式导入ANSYS中，选择两端与支撑轴承接触节点，施加X，Y和Z 3个方向全约束，有限元模态分析的第5阶和第6阶时的振型图如图3、图4所示，前6阶模态见表1。

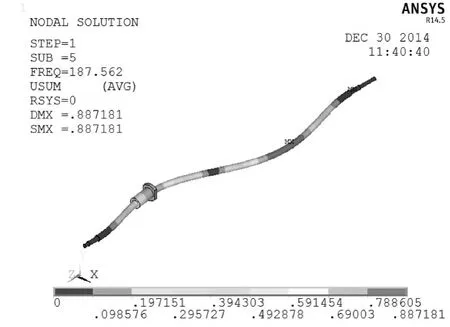
图3 第5阶振型图

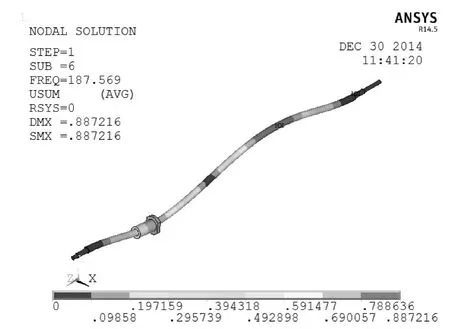
图4 第6阶振型图

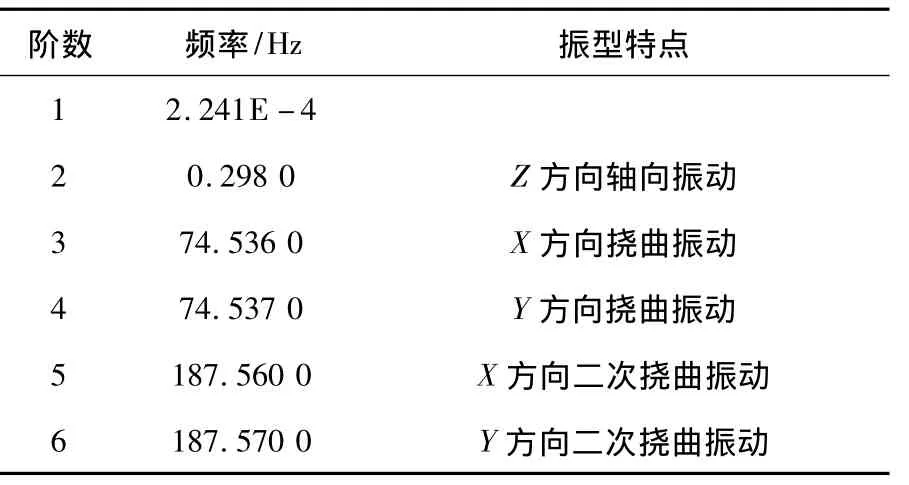
表1 螺母运动到最左侧时的前6阶模态

由表1可知:(1)第1阶、第2阶频率几乎为零，为刚体模态，可不考虑;(2)第3，4阶及第5，6阶固有频率很接近，振型状态近似于正交，这是因为模型的结构和约束都是对称的，相当于数学上的矩阵中一个特征值对应两个不同的特征向量;(3)根据转速n和频率f的关系(n=60f)，计算丝杠在刚体模态后的前两阶频率下的临界转速为4 472 r/min，明显大于所选丝杠的最大转速3 000r/min，因此丝杠在有效转速范围内不会发生共振。

2.1.2 螺母运动到中间时的模态分析

与螺母运动到最左侧时的操作相同，螺母运动到中间时的前6阶模态见表2。

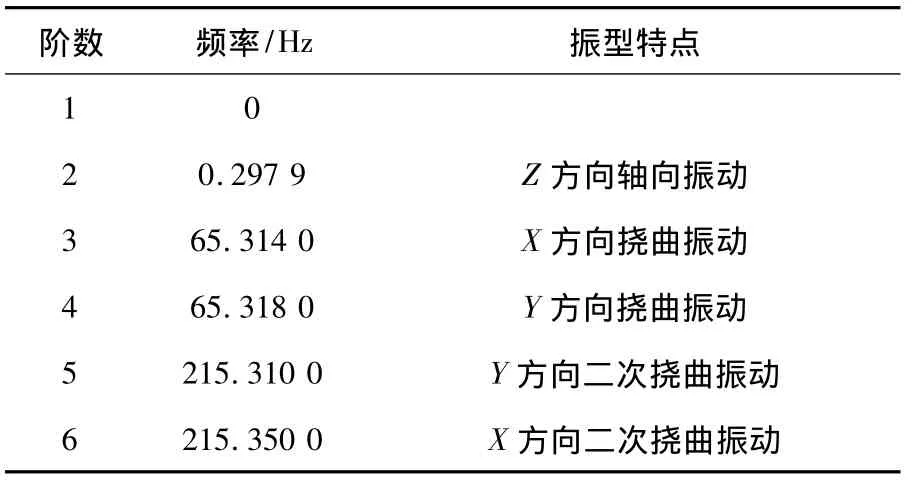
表2 螺母运动到中间时的前6阶模态

由表2可知:(1)因为第1阶频率为零，第2阶频率几乎为零，为刚体模态，可不考虑;(2)计算丝杠在刚体模态后的前两阶频率下的临界转速为3 918r/min，明显大于所选丝杠的最大转速3 000r/min，因此丝杠在有效转速范围内不会发生共振。

2.1.3 螺母运动到最右侧时的模态分析

同上操作，由于设计的滚珠丝杠螺母副的丝杠两端结构相同，只是支撑端伸出部分长度稍有差值(相差51mm)，但影响不大，分析结果与螺母在最左侧时的分析结果基本相同，这里就不多做赘述。

2.2 一端固定一端支撑方式的模态分析

2.2.1 螺母运动到最左侧时的模态分析

将Hypermesh划分好的网格以.cdb格式导入ANSYS中，选择两端与支撑轴承接触节点，固定支撑的一端施加X，Y和Z 3个方向全约束，支撑一端施加X和Y2个方向约束，螺母运动到最左侧时的前6阶模态见表3。

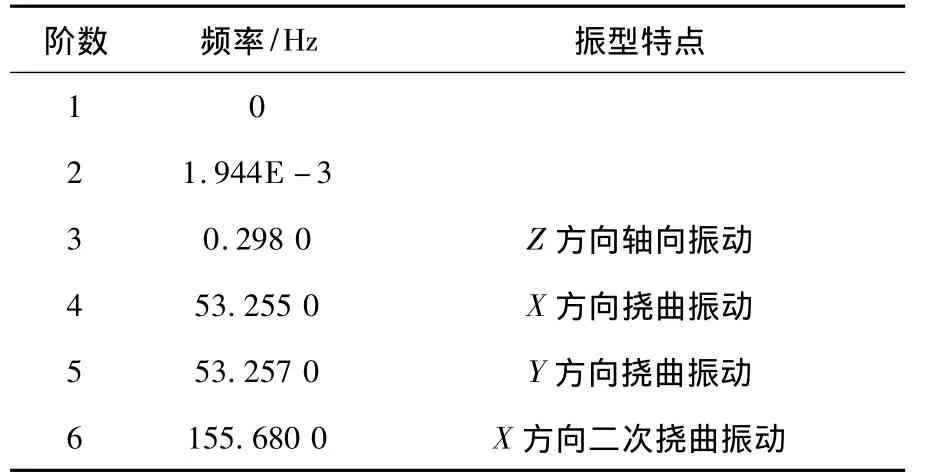
表3 螺母运动到最左侧时的前6阶模态

由表3可知:(1)因为第1阶频率为零，第2阶和第3阶频率几乎为零，为刚体模态，可不考虑;(2)计算丝杠在刚体模态后的前两阶频率下的临界转速为3 195r/min，大于所选丝杠的最大转速3 000r/min，因此丝杠在有效转速范围内不会发生共振。

2.2.2 螺母运动到中间时的模态分析

与螺母运动到最左侧时的操作相同，螺母运动到中间时的前6阶模态见表4。

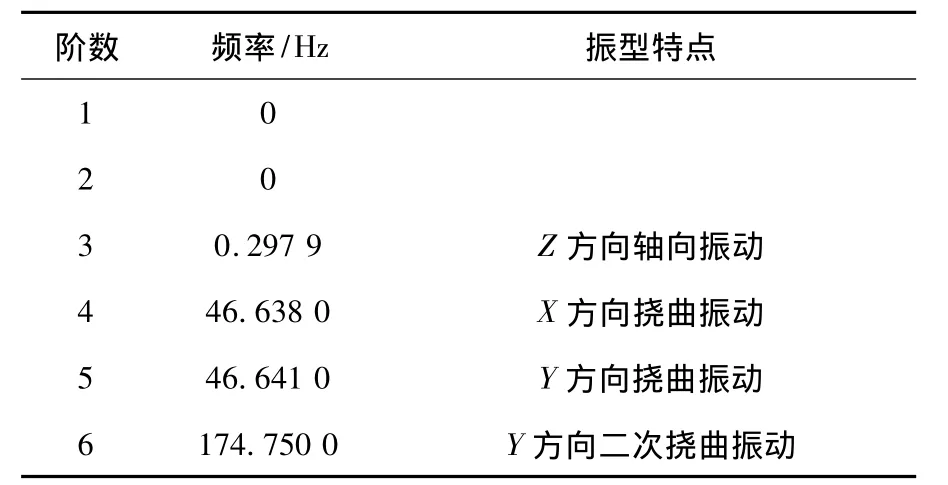
表4 螺母运动到中间时的前6阶模态

由表4可知:(1)因为第1阶、第2阶频率为零，第3阶频率几乎为零，为刚体模态，可不考虑;(2)计算丝杠在刚体模态后的前两阶频率下的临界转速为2 798r/min，小于所选丝杠的最大转速3 000r/min，因此丝杠在有效转速范围内会发生共振。

2.2.3 螺母运动到最右侧时的模态分析

与螺母运动到最左侧时的操作相同，螺母运动到最右侧的前6阶模态见表5所示。

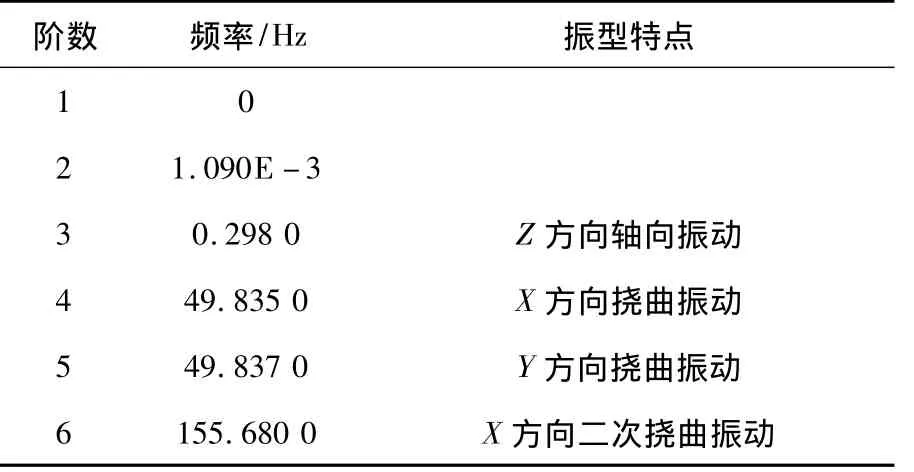
表5 螺母运动到最右侧的前6阶模态

由表5可知:(1)因为第1阶频率为零，第2阶和第3阶频率几乎为零，为刚体模态，可不考虑;(2)计算丝杠在刚体模态后的前两阶频率下的临界转速为2 990r/min，小于所选丝杠的最大转速3 000r/min，因此丝杠在有效转速范围内会发生共振。

3 滚珠丝杠螺母副的谐响应分析

模态分析反映的只是结构本身属性，进给系统在实际工作状况中会受到载荷作用，为了得到进给系统在不同频率载荷作用下的动态响应，需进行谐响应分析。下面针对两端固定支撑方式下的滚珠丝杠螺母副进行谐响应分析。

3.1 螺母运动到丝杠最左侧时的谐响应分析

考虑到实际工作状况，选择对丝杠施加幅值为1 000N的轴向简谐载荷，得到的谐响应曲线如图5所示。从图5可知，频率大约为74Hz时谐响应振幅最大，其值为2.34×10－6m，这个频率对应的是表1中丝杠第3阶模态的频率，此时的振型是X方向挠曲振动。因此，实际加工过程中，螺母运动到丝杠最左侧时，应避免在该频率下加载动载荷，以免引起机床较大的振动，影响机床的加工质量。

3.2 螺母运动到丝杠中间时的谐响应分析

同样对丝杠施加幅值为1 000N的轴向简谐载荷，得到的谐响应曲线如图6所示。从图6可知，频率大约为66Hz时谐响应振幅最大，其值为1.03×10－7m，这个频率对应的是表2中丝杠第4阶模态的频率，此时的振型是Y方向挠曲振动。因此当螺母运动到丝杠中间位置时，在此频率下也应当避免加载动载荷。

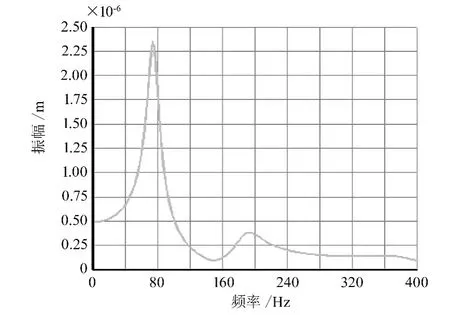
图5 螺母运动到丝杠最左侧时的谐响应曲线

图6 螺母运动到丝杠中间时的谐响应曲线

3.3 螺母运动到丝杠最右侧时的谐响应分析

其在1 000N正弦载荷激励下的谐响应分析结果与螺母运动到丝杠最左侧时的情况类似，这里就不再赘述。

4 结束语

本文通过合理简化，并以弹簧单元模拟丝杠滚珠与滚道之间的接触，建立了滚珠丝杠螺母副的有限元模型。针对滚珠丝杠螺母副的不同支撑方式和螺母运动位置，进行了模态分析，得到其固有频率和振型。比较分析结果得出:两端固定支撑方式时，丝杠在有效转速范围内不会出现共振现象;而一端固定一端支撑的滚珠丝杠螺母副，当螺母运动到丝杠中间至右端时都可能会发生共振现象。因此，建议滚珠丝杠螺母副采用两端固定支承方式。通过对滚珠丝杠螺母副进行在正弦载荷激励下的谐响应分析，得出滚珠丝杠螺母副两端固定支撑方式时各个运动状态的动态响应，以及最大振幅的频率。在实际工作状态中，应尽量不要在此频率范围内施加动载荷，避免引起机床的振动，以提高机床的加工精度。

［1］ 姜洪奎.大导程滚珠丝杠副动力学性能及加工方法研究［D］.济南:山东大学，2007.

［2］ 宁怀明，王彦红.滚珠丝杠基于ANSYS的动态分析［J］.煤炭技术，2010，29(7):18－19.

［3］ 谢黎明，闫冰，靳岚.基于有限元法的滚珠丝杠动态特性研究［J］.组合机床与自动化加工技术，2014(1):10－13.

［4］ 侯秉铎，许 瑛，彭浪草，等.超精密滚珠丝杠进给系统谐响应的有限元分析［J］.组合机床与自动化加工技术，2011(6):20－22.

［5］ 安琦瑜，冯平法，郁鼎文.基于FEM的滚珠丝杠进给系统动态性能分析［J］.制造技术与机床，2005(10):85－88.

［6］ 张东生，宁玮，宋春明，等.龙门式机床横梁结构有限元模态分析［J］.机械设计与制造工程，2014，43(5):21－23.

［7］ 许向荣.滚珠丝杠副直线导轨进给单元动态性能研究［D］.济南:山东大学，2011.

［8］ 许向荣，宋现春，姜洪奎，等.单螺母滚珠丝杠副轴向刚度的分析研究［J］.武汉理工大学学报，2009，31(24):54－57.