西安市PM2.5相关因素多元回归分析模型

刘文军　郑国义　田学　郎广名　冯倩

摘要 为了探索空气污染的主要因素，对空气污染监测指标PM2.5与AQI中其他监测指标进行相关性分析， 得到PM2.5与SO2、NO2、CO呈正相关， 与O3和温度呈负相关， 同时利用多元回归模型得到PM2.5与主因子的数量关系， 给西安市PM2.5防控提供参考意见.

关键词 PM2.5； AQI； 主成分分析； 多元回归模型

中图分类号 O213； X501 文献标识码 A

Abstract

To explore the main reason of air pollution， we analyzed the correlation between monitoring index of air pollution PM2.5 and other monitoring indexes of AQI， and found that PM2.5 was associated positively with SO2， NO2， CO， and negatively with O3 and the temperature. Then we got the numerical relationship between PM2.5 and the main factor according to multiple regression model. The results offers some references to the control of PM2.5 in Xi'an.

Key wordsPM2.5； AQI； principal component analysis； multivariate regression model

1引言

PM2.5导致的雾霾天气日益严重， 影响人们的身体健康及出行， 其引起社会的广泛关注1. 西安是典型的北方城市， 它被联合国开发计划署选列为大气颗粒物污染研究示范性城市2， 由于西安特殊的地理位置， 被称为“污染天井”， 并且冬季燃煤取暖、人口密集， 因此本文以西安市为研究对象.

大气污染的两个基本要素是大气气溶胶和气态大气污染物3. 周顺武等4利用SO2、NO2、PM10三项指标， 分析了污染物浓度的分布特征.

李伟等5利用AQI指标的六项监测数据得到PM2.5与其他五项之间的关系. 通过已经公布的历史数据可以发现PM2.5影响因素具有不确定性， 所以本文采用统计学的多元回归模型探究PM2.5与AQI其他监测指标及温度因素的关系得到精确的统计模型， 发现PM2.5的测量值在春季、冬季相对较高， 在夏季、秋季较低6， 本文对温度因素与AQI监测指标进行相关分析， 得到PM2.5与其他监测指标的数量关系， 为西安市环保部门防治空气污染提供参考意见.

2数据来源及指标选择

通过西安市环保监测站查找了2013年1月1日～2013年12月31日的AQI监测数据， 温度数据来源于中国天气网的西安市天气历史数据. 选取的9个指标， 分别是PM2.5（PM2.5日平均浓度值， 单位μg/m3）、SO2（SO2日平均浓度值， 单位μg/m3）、NO2（NO2日平均浓度值， 单位μg/m3）、CO（CO日平均浓度值， 单位μg/m3）、O3-1（臭氧1个小时平均浓度值， 单位μg/m3）、O3-8（臭氧8个小时平均浓度值， 单位μg/m3）、PM10（可吸入颗粒物PM10日平均浓度值， 单位μg/m3）、Tmax（日温度最高值， 单位℃）、Tmin（日温度最低值， 单位℃）.

3数据预处理

为了保证数据的完整性， 需要对数据进行缺失值查找和填补， 利用SPSS 21.0 统计软件7对各个变量进行变量的基本统计分析， 发现2013年3月25日O3-8指标缺失， 因此本文采用回归的方法对该数据进行填补， 保证了数据的完整性. 为了消除数据变量在数量级和量纲上的不同， 将填补缺失值后的完整数据进行标准化处理. 本文采用的是Z标准化， 即数据处理后的均值为0， 方差为1.标准化公式为： x*=x-μσ， 其中μ为样本数据的均值， σ为样本数据的标准差.

4PM2.5与其他指标的多元回归分析

对AQI的7个基本监测指标及每日最高温度、最低温度的相关性进行定量分析， 尤其是对PM2.5含量与其他8项分指标数量的相关性及其数量关系进行分析， 可以从两个方面进行考虑： 第一， PM2.5与其他8项指标之间的相关性； 第二，PM2.5与其他指标间存在的数量关系.

4.1PM2.5相关因素相关性分析

复相关分析法能够反映各要素的综合影响， 几个要素与某一个要素之间的复相关程度， 用复相关系数来测定. 复相关系数可以利用相关系数和偏相关系数求得， 其假设检验与多元回归的方差分析结果一致， 因而表示回归贡献的百分比值. 复相关系数的取值介于-1与+1之间， 用其绝对值的大小来判断相关的密切程度， 绝对值越大， 相关性越大； 反之， 相关性越小. 本文利用复相关分析方法， 并利用SPSS 21.0软件进行数据分析. 具体步骤如下：

1）利用SPSS 软件对SO2、NO2、PM10、CO、O3-1、O3-8、Tmax、Tmin和PM2.5这9个指标进行相关分析， 采用Pearson相关分析法得到表2的数据. 数据结果显示PM2.5与SO2、NO2、PM10、CO、O3都是相关的， 并且存在较高的相关系数， 尤其与PM10的相关性最大.

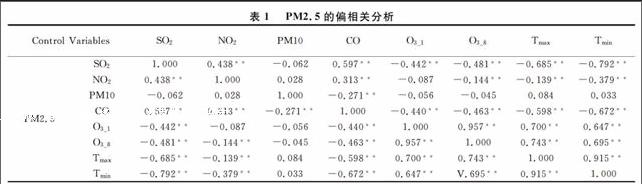
2）利用SPSS 21.0软件先固定PM2.5， 再对其余指标进行偏相关分析， 得到表1.

3） 计算复相关系数为0.996 0.

通过以上分析， 可以得到以下结论， PM2.5与PM10的相关系数最高， 相关系数为0.887， 说明PM10对于PM2.5的影响最大； 其次PM2.5与CO的相关系数为0.821， 也说明了它们相关性较高； 再次NO2、SO2与PM2.5的相关系数也是比较大的， 说明已有的研究结论是合理的， 即二氧化硫（SO2）， 二氧化氮（NO2）， 一氧化碳（CO）是在一定环境条件下形成PM2.5的主要气态物质； 但是O3-1与PM2.5的相关系数为-0.235， O3-8与PM2.5的相关系数为-0.274， Tmax与PM2.5的相关系数为-0.530， Tmin与PM2.5的相关系数为-0.523， 呈现负相关， 说明O3与温度对PM2.5可能有一定的抑制作用.

4.2PM2.5与其他指标的多元回归分析

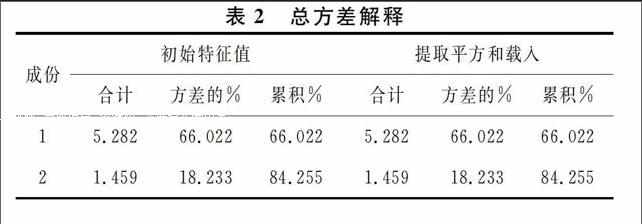
多元回归分析7是一种处理一个因变量与多个自变量关系的方法， 通过多元回归分析， 能够得到因变量与自变量的数量关系. 根据表2（Pearson相关分析）， 可以发现这9项指标存在不同程度的相关性， 其中PM10与PM2.5， CO与PM2.5， SO2与PM2.5， SO2与NO2， NO2与PM10， NO2与PM2.5之间都具有较大的相关性， 但是建立多元回归模型需要保证指标间的独立性， 本文采用主成分分析法对9个指标进行分析， 然后再建立PM2.5与主成分之间的多元回归模型. 对SO2、CO等指标进行主成分分析结果见表2.

5总结与建议

本文利用数学建模的思想研究西安PM2.5的污染问题， 收集并整理了西安市2013年AQI和温

度的监测数据， 对西安市2013年的PM2.5与AQI其它监测指标和温度进行相关性分析， 发现PM2.5与PM10、NO2、SO2、CO呈正相关， 与O3-1、O3-8和温度呈负相关， 探索了PM2.5与其他变量的数量关系，但通过前面的讨论，较高的相关性不适合进行多元回归建模，因此本文利用主成分分析消除变量间的相关性， 得到两主成分， 最后利用多元回归模型， 得到了PM2.5与主成分的关系， 可以发现PM2.5与O3-1、O3-8和温度仍然呈现负相关， 而与PM10、NO2、SO2、CO呈正相关是一致的， 并且可以得到较为精确的统计模型， PM2.5与AQI和温度数据关系提供一定的参考依据， 并且对西安市PM2.5防控具有指导意义.

因此， 要加强对建筑工地扬尘工作的管理； 加大城市建设管理力度； 加强城市绿化， 增加植被覆盖； 政府要推行多举措， 多污染物联合防治， 改变经济发展模式和能源结构方式， 达到长期减排减少污染的目的.

参考文献

1陶燕， 刘亚梦， 米生权， 等. 大气细颗粒物的污染特征及对人类健康的影响J. 环境科学学报， 2014， 34（3）： 592-597.

2戴树桂. 环境化学（第二版）M. 北京： 高等教育出版社， 2001： 227-239.

3王玮， 汤大钢， 刘红杰. 中国PM2. 5污染状况和污染特征的研究J. 环境科学研究， 2000， 13（1）： 1-5.

4周顺武， 黄琼中. 拉萨市空气污染物浓度的统计分析及其可能的天气原因J. 西藏科技， 2002， 109（5）：39-42.

5李伟， 姜志平， 李俊坡， 等. PM2.5相关因素分析及其演变预测J. 现代电子技术， 2014， 37（18）： 63-69.

6林启才， 张振文， 杜利劳， 等. 2013年西安市大气污染物变化特征及成因分析研究J. 环境科学与管理， 2014， 39（10）： 52-55.

7薛薇. 统计分析与SPSS 的应用（第二版）M. 北京： 中国人民大学出版社， 2008.