基于熵算法的股票指数高频数据复杂度测算与评价

温博慧+袁铭+侯笠

摘要 在日内高频环境下检验基于兼容法的柯尔莫哥洛夫熵、样本熵和模糊熵等复杂度测算方法对我国沪深300股票指数的测算效率，并运用筛选后的有效算法分阶段研究和比较了序列复杂度的变化过程与变化幅度.结果表明，模糊熵算法是一种更适用于我国沪深300股票指数的有效复杂度测算方法，其对相似容忍度的敏感性更低，测度值连续性更好.随时间推移，我国沪深300股票指数复杂度整体呈上升趋势，而相较于发达市场甚至周边新兴市场其复杂度偏低.

关键词 沪深300股票指数；复杂度；kolmogorov熵；样本熵；模糊熵

中图分类号 F830 文献标识码 A

AbstractThis paper studied the high frequency data of the CSI 300 index， and examined the efficiency of complexity measures such as Kolmogorov entropy， sample entropy and fuzzy entropy in high frequency environment. By using the effective measurement， it compared the changing process and range of the complexity both before and after the subprime crisis. The results show that， compared with the Kolmogorov entropy based on the compatible method and sample entropy， fuzzy entropy is more suitable for measuring the CSI300 index's complexity， which has the lower sensitivity to the similar tolerance and the better continuity of measure value. The CSI 300 index's complexity is rising during the sample interval. However， the complexity during the crisis is far more less than the two other stages， and the complexity after the crisis is higher than that before the crisis. Compared with the developed markets and even some emerging markets， the CSI 300 index's complexity is much lower.

Key wordsthe CSI 300 index； complexity； Kolmogorov entropy； sample entropy； fuzzy entropy

1问题提出与相关文献回顾

根据混沌理论，复杂度被定义为非线性动力系统或序列的复杂性程度[1].其大动态范围、短平稳性和小数据量的特征被认为是最适于分析非线性系统的动力学特征参数，也是非线性动力系统研究的重要方面[2].沪深300股票指数是联系我国股票现货市场与股指期货市场之间的重要桥梁，金融机构往往需在日内动态调整资产头寸并关注风险管理，因此，沪深300股票指数高频数据的复杂性程度对于风险管理和交易策略实施均具有重要意义.在我国市场环境下，有效地复杂度测算方法是什么？与成熟市场和周边的新兴市场相比，我国沪深300股票指数的复杂度如何？围绕次贷危机的影响，不同时间阶段其复杂度的变化幅度与变化过程如何？既有研究尚未对上述系列重要问题做出较为全面地解答，同时学术界和实务界对采用何种方法来进行复杂度测算亦尚未达成共识.

早期文献表明，关于混沌序列复杂度的研究始于20世纪60年代.西方学者提出了各种相关测度指标与方法，但成果主要集中于工程计算领域.随着金融市场非线性动力学行为与混沌效应的存在性逐渐得到实证，关于股价波动复杂度的测算研究成为热点，但方法局限于围绕分形维数的测算，研究结论也在多重分形错觉方面存在较大争议[3，4].

近年来，学者们运用不同类型的熵模型展开了复杂度测算研究，主要包括柯尔莫哥洛夫熵（kolmogorov）、近似熵（ApEn）、样本熵（SampEn）和模糊熵（FuzzyEn）算法.kolmogorov（1965）将复杂度界定为能够产生某一（0，1）序列所需的最短程序的比特数，并形成Kolmogorov熵算法.Lempel和Ziv（1976）给出了其在计算机中实现的具体算法.对此，肖辉，吴冲锋，吴文峰，等（2002）将之应用于中国股票市场检测，计算了沪市综合指数与深市成份指数的复杂度[5].尽管该算法有着严格的数学理论基础和依据，但因需将给定时间序列转换成符号序列，使得转换方法成为该算法在股价波动复杂度测算应用时的关键.然而，均值法、极值法和遗传密码法三种主要转换方法均未考虑序列整体性质，亦不能区分弱混沌与周期序列，以及强混沌与随机序列（Abuasad， ect.， 2012）[6].综合法（He，Xu，2000）为解决上述问题，按不同时间序列分别应用均值法和极值法，但受限于需事先明确知道时间序列性质（赵波等，2014）.对此，王福来和达庆利（2007）提出了基于兼容法的Kolmogorov熵算法并应用于上证综合指数日收盘价序列复杂度测算[7]，为Kolmogorov熵算法缺陷问题的解决提供了新视角.

由于近似熵算法（Pincus，1995）采用Heaviside函数进行相似性量度，敏感于阀值和相空间维数，从而参数选取会使其计算精度带有经验性（蔡觉平，李赞，宋文涛，2003）.样本熵算法通过不计算自身匹配的统计量，对其形成了改进，但在无模板匹配的情况下可能出现ln0的无意义结果（贺少波，尹林子，阿地力·多力坤，2012）.对此，学术界相继提出了多种改进方法.肖方红，阎桂荣和韩宇航（2004）将混沌伪随机序列看成符号序列，提出符号熵算法.虽然该算法不涉及参数的选取，计算比近似熵算法更为简单，但符号熵算法需预先知道符号空间，且只针对伪随机序列，应用范围局限性较大.Chen（2011）在对样本熵（SampEn）进行改进基础上提出模糊熵（FuzzyEn）算法，并基于TDERCS系统成功检验了其有效性（贺少波，尹林子，阿地力·多力坤，2012）[8].模拟显示，基于模糊熵的复杂度测算方法可能在对参数依赖的敏感性方面更低，测度值的连续性更好，从而获得更高的测度效率（李鹏，等，2013）[9].

文章的创新之处在于：1）不仅较为全面的对比了各种基于熵算法的复杂度模型测算效率，而且进行了小样本修正，以期为沪深300股票指数复杂度测算提供可靠的实证依据与分析结论.2）围绕次贷危机的影响分阶段研究和比较了危机前、中、后期序列复杂度的变化过程与变化幅度，并与发达市场乃至周边新兴市场股指期货标的指数的复杂度相较，得到我国沪深300股票指数复杂度的演化规律与独特性质.

2代表性熵算法、有限样本修正

与测算效率评价标准

通过对相关研究成果的梳理可知，对既有测算效率形成一定改进后的代表性熵算法主要集中为基于兼容法的Kolmogorov熵、样本熵和模糊熵.重构相空间维数m、相似容限度r和序列长度N是测算过程中的共同关键变量.如模糊熵：

当时间长度足够长时，MFDFA方法计算得到的h（q）是较准确的，但在实际应用中，序列长度很难满足要求，此时有限样本会使h（q）的计算产生偏误，进而也会使关联维数以及熵计算中的相空间维数m产生偏误，因此需要对MFDFA中的有限样本效应进行修正，以提升测算和评价结果的准确性.修正方法基本思路为：利用Liu（2007）和吴栩等（2014）对马尔科夫转换多重分形模型（MSM）的解析，构造能够尽可能反映原始股指序列多重分形特征的模拟序列，该模拟序列的长度应该足够的长，从而可以消除MFDFA计算中的有限样本效应.

在测算复杂度的过程中，对模型效率的评价标准主要集中于算法本身的稳定性和结果对模型参数的依赖程度，即，算法鲁棒性，对相空间维数、相似容限度和时间序列长度的敏感性和依赖性，以及测度结果的连续性[11].由于是对我国沪深300股票指数运动的复杂度进行测算，而复杂度的标准值尚未知，不同于在某些性质既定和已知正确结果的复杂系统下对研究方法的评价，因此，通过算法鲁棒性来评价模型效率的路径尚不能行通.在熵算法模型中股指序列长度N既定，相空间维数m通过计算获得，测度值对参数的敏感性和依赖性，以及结果的连续性主要与相似容限度r密切相关[12].因此可以认为，当在相似容限度的经验取值范围内，某一算法未出现错误度量值，其测度结果趋于稳定且图像相对平滑，则该算法对相似容限度的敏感性和依赖性较低，测度效率相对较高.

3数据说明与采样频率筛选

以2005年5月9日至2013年12月31日沪深300股票指数1分钟、5分钟、10分钟、15分钟和60分钟高频数据

选择了相关研究中主要出现的若干种高频频率作为筛选对象.作为基础研究样本.数据来源为Reset数据库.虽然我国沪深300股票指数于2005年4月8日上市，但考虑到上市之初，市场各方对该指数存在熟悉过程[13]，为准确起见，在数据选取时剔除掉了2005年4月的交易数据.

直接采用股票指数而未如传统证券市场定量分析采用收益率数据 在有关证券市场的定量分析中通常使用收益率样本而不是指数本身，主要是考虑到价格序列的相关性违反以高斯假设和正态分布为基础的线性分析框架原则.，主要缘于文章的复杂性研究视角，避免收益率变量可能对系统非线性相依结构所形成的破坏.

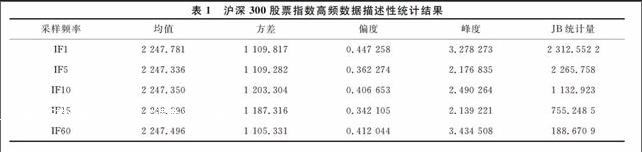
沪深300股票指数1分钟、5分钟、10分钟、15分钟和60分钟高频数据的描述性统计结果如表1所示， 其中IF1、IF5、IF10、IF15和IF60依次对应不同采样频率.统计结果显示，各种不同采样频率的高频数据都表现出有偏和尖峰厚尾的统计特征，且明显超出了正态分布假定的范围（JarqueBera统计量显著） .因此，可以认为各序列明显具有非线性特质.

鉴于不同采样频率可能会带来不同检验结果，在进行复杂度测算之前需要进行有效采样频率甄别.由既有熵测算方法可知，相空间维数是各熵算法中的关键变量.较窄的多重分形度置信区间对应较精确的维数.因此，遵从多重分形度置信区间计算方法，以对多重分形度置信区间宽度的比较筛选有效高频采样频率，比较结果如表2所示.

根据表2结果可知：各采样频率下经有限样本效应修正后的多重分形度均仍接近于1，我国沪深300股票指数运行具有多重分形特征；置信区间宽度随采样间隔的增加而变化，其中当间隔为5分钟时宽度最窄.从而，沪深300股票指数5分钟高频数据为进行复杂度测算的有效采样频率数据.

为方便与发达市场和周边新兴市场的股指期货标的指数复杂度的对比，文章还选择了标准普尔500指数、日经225指数和韩国指数2005年5月9日至2013年12月31日的5分钟高频数据，作为第四部分对比分析中的研究数据.

4沪深300股票指数高频数据复杂度的

熵测算实证结果与分析

由于涉及了三种熵算法模型，且模型中至少涉及了三种关键参数，为了清晰起见，此处不逐一报告参数的估计结果，而是直接展示对应熵算法下的复杂度结果，及其随关键参数值改变而变化的过程，并进一步进行模型测算效率评价.

4.1关键参数值的确定

由熵算法步骤可知，重构相空间维数m、相似容限度r和序列长度N是测算过程中的关键变量，需要对其进行准确数值确定.

在上述三变量中，时间序列长度N由给定样本区间决定.经筛选，研究中的基础样本为2005年5月9日至2013年12月31日的沪深300股票指数5分钟高频数据，时间序列总长度N= 689 330.

相似容限度r属于熵算法模型中的阀值变量，其值过小会增加结果对噪声的敏感性，过大则会导致信息丢失，根据Chen（2009）的模拟建议，r的取值一般可在[0.3，0.35]中选取.

对相空间维数m的选取，相关研究通常使用经验值.由于尽管较大的m能细致重构系统的动态演化过程，但亦会陡增运算量，m取值通常为2、3、4、5和6.为了更为准确衡量指数复杂度，可以基于所提出的有限样本修正方法计算获取合理m值.依第二部分中的修正算法得到测算后的适宜m值为3

鉴于篇幅有限，小样本修正的计算步骤在此不作列示，仅给出最后结果.有兴趣的读者可与作者联系..

4.2全样本区间内的测算结果与模型测算效

率比较

基于兼容法的Kolmogorov熵算法的计算结果显示，全样本区间内我国沪深300股票指数的复杂度为1.057 1，超出了该算法复杂度值的（0，1）值域.考虑到全样本区间可能因数据存在结构突变而导致虚假统计结果，运用计算程序每次取其连续的1 000个数据在有限样本效应修正下进行分析，然后取其均值作为序列平均复杂度.结果显示，平均复杂度为1.049 9，依然超出了Kolmogorov熵算法复杂度的值域范围.说明基于兼容法的Kolmogorov熵算法并不适用于对我国沪深300股票指数复杂度的测算

其原因可能缘于该算法在序列复杂度接近于1时分辨率不高.但整体结果与分段后均值结果均超出了值域范围，已经说明该方法失效.文章并不旨在分析该方法失效的原因，因此不再对此进行深入说明..

图1（a）、（b）依次显示的是样本熵和模糊熵两种算法对复杂度的估计结果.虽然相似容限度r的经验值取范围为[0.3，0.35]，但为了更便于分析研究方法的效率，在编写程序过程中令r从0到0.5以0.001等间距变化

以0.001的间距变化趋近连续变化.，并对应计算复杂度值，以观察结果的连续性及其对参数变化的敏感程度.从图1（a）（b）中可以看出，样本熵和模糊熵算法均测出了复杂度计算结果，且计算结果整体比较接近.复杂度值均随r的增大而减小，当r取值为[0.3，0.35]时，其所估计的沪深300股票指数复杂度值相对其他区间内的复杂度值平稳，数值在0.55到0.43之间（如图1（a）和（b）中的虚线区域部分）.

相似容限度（a）样本熵算法下沪深300股票指数复杂度的估计结果

相似容限度（b）模糊熵算法下沪深300股票指数复杂度的估计结果

在测度结果的连续性与对参数的敏感性方面，样本熵测度结果在r的整个取值范围[0，0.5]内出现多个跳跃点，且在[0.3，0.35]范围内的跳跃点明显多于模糊熵（如图1（a）中的虚线区域部分），说明模糊熵算法相对于样本熵算法对相似容忍度的敏感性更低，测度值的连续性更高.有限样本效应修正后，当r取[0.3，0.35]时，模糊熵算法下的复杂度均值为0.494 9.

4.3不同时段沪深300股票指数复杂度结果

比较

为进一步刻画我国沪深300股票指数复杂度，在对测算方法评估后，本部分基于模糊熵算法，对全样本区间内不同时段复杂度进行测算比较.

从2005年5月9日至2013年12月31日的全样本区间可划分为2005年5月9日到2007年9月30日的指数高速攀升阶段，2007年10月8日到2009年3月31日的危机阶段和2009年4月1日到2013年12月31日的后危机阶段（其涵盖了我国股指期货从2010年4月16日推出并运行至今的阶段）三个阶段.各阶段复杂度值如表3所示.

虽然各阶段时间序列长度不尽相同，但由于模糊熵算法优于样本熵和Kolmogorov熵复杂度算法，且当N值在10 000左右时，模糊熵算法本身具有对时间序列长度较高的一致性，经有限样本效应修正后此种一致性效果会进一步增强.因此，分阶段后时间序列长度的不一致并不会对分阶段研究的计算结果形成显著影响.

如表3所示，各阶段复杂度测算结果表明，在危机前中国股市的集中上涨时段，指数复杂度为0.462 3；指数受危机冲击而大幅下挫阶段的复杂度为0.427 1；后危机时代的指数复杂度为0.510 2.其说明我国沪深300股票指数复杂度以后危机时代阶段为最高，受危机冲击阶段为最低.

美国次贷危机前我国股票指数运行表现为整体性快速上涨，受危机影响阶段表现为指数整体大幅下挫，两阶段股指运行均呈现出较强规律性，其市场投资者行为较单一，符合规律性序列复杂度较低的复杂度数值性质.而指数下跌阶段复杂度低于上涨阶段复杂度，则提示出沪深300股票指数在下跌阶段趋势性更强.这一点与股指波动非对称性（陈浪南，黄杰鲲，2002；陆贤伟，董大勇，纪春霞，2009；顾锋娟，金德环2013）特征一致.指数在后危机时代复杂度得到提升，说明危机冲击及相关股市政策改革后，我国沪深300股票指数运行的单一趋势性有所转化，投资者行为多样性得到补充；同时，在后危机阶段我国股指期货正式推出运行，也说明股指期货的推出对打破股票市场运行单一趋势性与修正波动时间一定程度上发挥了作用.

4.4不同市场股指期货标的指数复杂度比较

为了便于与发达市场和周边新兴市场的股指期货标的指数复杂度进行对比，此处选择了标准普尔500指数、日经225指数和韩国指数2005年5月9日至2013年12月31日的5分钟高频数据作为对比样本.基于模糊熵算法，全样本区间内发达市场和周边新兴市场的股指期货标的指数复杂度测算结果如表4所示；2009年4月1日到2013年12月1日的后危机阶段的复杂度测算结果如表5所示.

通过对比各个不同股票市场的复杂度，不难发现，无论是全样本区间还是后危机阶段，发达股票市场的复杂度均大于我国股票市场的复杂度；其中，我国沪深300股票指数复杂度以与标准普尔500指数复杂度差距为最大，与韩国指数复杂度最为接近；而在后危机阶段，我国沪深300股票指数运行的复杂度较其他国家股指期货标的指数复杂度的差距均有所减小.说明，我国沪深300股票指数相对于代表性发达市场和周边新兴市场股指期货标的指数的可预测性更明显，潜在的市场投机性更大；而随着我国股票市场相关监督和运作体系的完善以及股指期货的推出，市场逐渐成熟，可预测性有所降低，投机性正在逐渐被削减.

5结论

文章对我国沪深300股票指数高频数据复杂度测算方法及复杂度特征进行了研究.通过运用3种新兴主流熵算法以及有限样本效应的修正，研究了3种算法对沪深300股票指数复杂度测算适用性以及不同时段和不同市场对比下我国沪深300股票指数复杂度变化和差异.

主要实证结果显示： 第一，在日内高频数据环境下，与基于兼容法的kolmogorov熵和样本熵算法相比，模糊熵算法是一种更适用于研究我国沪深300股票指数的有效的复杂度测算方法.其对相似容忍度参数的敏感性更低，测度结果的连续性更好.第二，随着时间的推移，我国沪深300股票指数序列复杂度整体呈上升趋势.但危机中阶段指数序列的复杂度远小于危机前后两阶段的复杂度，后危机阶段复杂度高于危机前阶段复杂度；相较于危机中阶段，后危机阶段复杂度的上升速度较快.第三，相较于发达市场甚至周边新兴市场股指期货标的指数，我国沪深300股票指数的复杂度呈现偏低结果.

针对实证研究的政策建议如下：

第一，鉴于虽然在后危机阶段（包括股指期货的推出）我国沪深300股票指数复杂度得到了快速上升，但与其他市场股指期货标的指数运行情况相比仍然偏低.而比较公认的观点是，偏低的复杂度对应市场投资者行为多样性不足，市场运行的不可预测性较弱.因此，为了稳定沪深300股票指数运动，减少较多一致性投机行为，增加机构投资者参与数量，提高预测难度.

第二，由于多种类型机构投资者可以丰富不同环境下期货与现货指数市场的投资行为，并对市场稳定起到积极作用从而提升市场复杂度（魏宇，赖晓东，余江，2013），目前我国还需转变机构投资者投资策略，避免一致性追涨杀跌，引导机构投资者端正投资理念，发挥其在股票市场中的稳定作用.

第三，由于实证结果表明，在日内高频环境下，模糊熵算法具有更好的适用性.因此，在监测沪深300股票指数复杂度时可采用该方法进行测算，以便获得更为准确的结果.基于兼容法的kolmogorov熵算法虽然较基础性kolmogorov熵算法形成了改进，但分析结果也表明了其对我国沪深300股票指数的不适用性.虽然在研究过程中还可对其形成进一步改进，但其计算过程相较于模糊熵算法的繁琐性也是明显的.因此，如果考虑到运算成本和使用难度等问题，模糊熵算法是监测我国沪深300股票指数复杂度的不错选择.

参考文献

[1]张林，李荣钧，刘小龙. 基于小波领袖多重分形分析法的股市有效性及风险检测[J]. 中国管理科学，2014，22（6）：17-26.

[2]陈小军，李赞，白宝明，等. 一种确定混沌伪随机序列复杂度的模糊关系熵测度[J]. 物理学报，2011，60（6）：064215.

[3]魏宇，赖晓东，余江.沪深300股指期货日内避险模型及效率研究[J].管理科学学报，2013，16（3）：29-40.

[4]周炜星.上证指数高频数据的多重分形错觉[J].管理科学学报，2010，13（3） ：81-86.

[5]肖辉，吴冲锋，吴文峰，等.复杂性度量法在股票市场中的应用[J].系统工程理论与实践，2002，11（3）：190-197.

[6]A ABUASAD，M I ALSMADI. Evaluating the correlation between software defect and design couping metrics[C]//2012 International Conference on Computer Information and Telecommunication Systems（CITS）. Washington DC： IEEE Computer，2012：1-5.

[7]王福来，达庆利.Co复杂度的改进及其在证券市场中的应用[J].数学的实践与认识，2007，37（8）：20-25.

[8]贺少波，尹林子，阿地力·多力坤.模糊熵算法在混沌序列复杂度分析中的应用[J].物理学报，2012，61（13）：130507.

[9]李鹏，刘澄玉，李丽萍，等.多尺度多变量模糊熵分析[J] .物理学报，2013，62（12）：120512.

[10]J KANTELHARDT，S ZSCHIEGNER. Multifractal detrended fluctuation analysis of nonstationary time series[J]. Physica A，2004（2）：49-83.

[11]I SOROKIN. Comparing files using structural entropy[J]. Journal in Comuter Virology， 2011， 7（4）：259-265.

[12]Ruipeng LIU， T D MATTEO， L THOMAS. True and apparent scaling： The proximity of the Markovswitching multifractal model to longrange dependence[J]. Physica A： Statistical Mechanics and its Applications，2007，383（1）：35-42.

[13]陈飞跃，杨蓉，龚海文.混合分数布朗运动环境下欧式期权定价[J].经济数学，2014，31（3）：9-13.